Pythonを使って45秒で東大の入試問題を１問解けるのか検証してみました。
Sympyの integrate(f, (x, a, b))を用いれば
関数fをxについてaからbまで積分計算することができます。
では早速問題を見てみましょう。
問題：
2019年 東京大学 前期日程 数学（理科） 第1問
読売新聞オンラインより問題および解答部を引用
手計算での解法
まずは上記の式を展開して、
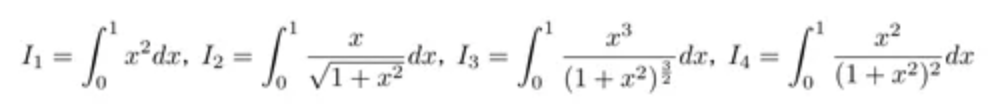
展開した第1項目から4項目までの定積分をそれぞれ計算して最後に
足し合わせます。
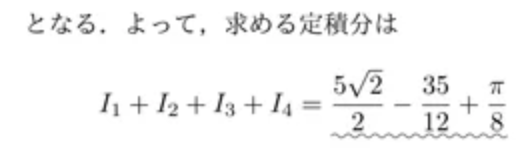
Sympyで解いてみる
まずはSympyをImportして変数xを定義
import.py
import sympy as sym
x = sym.Symbol('x')
間違えないようにひたすら式を打ち込む
念の為、表示して確認。
import.py
f = (x**2+x/sym.sqrt(1+x**2))*(1+x/((1+x**2)*sym.sqrt(1+x**2)))
print(f)
出力：(x2 + x/sqrt(x2 + 1))*(x/(x2 + 1)(3/2) + 1)
打ち間違えがなさそうなら
いよいよ０から１まで積分
integrate.py
F = sym.integrate(f, (x, 0, 1))
print(F)
出力：-35/12 + pi/8 + 5*sqrt(2)/2
解けました。
解答例と比べても合っているようです。
結論
高速でタイプしてギリいける感じです。
ちなみに１回目は式に目が慣れていなかったので失敗。2分以上かかりました。
よって45秒以内に解を出すにはいかに早く打てるかが鍵となります。
特に途中でタイプミスがあると致命的。
リズムに乗るために本家の45秒を聴きながらやってみるのも良いでしょう。
