D-Wave量子アニーリングマシンでマインスイーパ解いてみた

はじめに

東北大学で主催している量子アニーリングマシンのワークショップに参加していて、D-Waveマシンの使い方を覚えたのでマインスイーパを量子アニーリングで解いてみました。
とりあえず、作ってみた粗い内容なので説明追加の依頼があればできるだけ対応します。

下記は、ワークショップの公式ページと過去4回分の講義のYoutubeアーカイブです。
Youtubeの再生時間見るとびっくりしますが、参加者の質問に大関先生が文字通り”全て”答えています。
授業に使ったJupyter-notebookがgoogleコラボラトリーに用意されているので、プログラミング初心者の方でもはじめられる内容になっています。

授業でカナダのD-Waveマシンに指令出して計算する方法も解説しています。

これまで4回分の講義動画

この授業を無料で受けられる、しかも後から見直せるのは素晴らしい時代です！

本記事では、量子アニーリングや組合せ最適化問題の詳細な説明は、これら講義にお任せするとして、、
本格的な実応用を検討するワークショップの前に個人的に練習で作ってみた量子アニーリングでマインスイーパを解くプログラムを解説してみます。

D-Waveマシンの利用

D-Waveのクラウドサービスに登録すると無料で1分間分、量子アニーリングマシンを使うことができます。
1分間は少なく見えますが、一度の計算のはデフォルトで20μ秒なのでたくさん使えます。
本記時のコードをD-Waveの実機に計算させる場合は、アカウント登録してAPI-tokenを取得する必要があります。

量子アニーリングで解ける問題

詳しい解説は、大関先生の授業のYoutubeを見てください。
組合せ最適化問題を上手に解くことができます。
世の中のどんなことが組合せ最適化問題として扱えるのか考えていくことで量子アニーリングの利用が広がっていきそうです。

マインスイーパを量子コンピュータで解くために

マインスイーパ

Windowsのゲームにいて授業や仕事が退屈な時のお供だった、あのゲームです。

ルールを箇条書きにしてみると下のような感じです。

1. 初期情報としてプレイヤーには設置された地雷の数が情報として与えられる。
2. 地雷の入っていないと思うマスを開いていく。
3. 開いたマスに地雷が無ければ、そのマスの周囲8マスにある地雷の数が与えられる。開けたマスの周囲に爆弾
4. がなければ、爆弾に隣接するマスまで一気に開く。
5. 地雷の入っているマス以外全てのマスを開けるとプレイヤーの勝ち。
6. 開いたマスに地雷があれば負け。

量子アニーリングで解く方法を考える

マインスイーパを解くときはヒントして表示される８Cell(マス)の爆弾の数を頼りに、そこに隣接する８Cellの爆弾のあるなしを予想します。

量子アニーリングのqbitは0,1を出力してくれるので、

• 爆弾がある状態:1
• 爆弾がない状態:0

としてヒントのCellの隣接する8Cellを量子アニーリングで爆弾のある/なしを予測します。
ヒントの数字のCellを見つけて、その隣接で開いていないCellにqbitを配置する。
マインスイーパはそもそも確率の問題になる部分があるので、量子アニーリングで何回も解かせてその平均を確率として出させる。

基本の
(隣接するCellの出力の合計) - (ヒントの数字) = 0
を満たすようにCellに0/1を配置すれば良いということになります。
ヒントの数字はたくさんあるので、重ね合わせてこれを満たすようにすれば良いということ。

ちゃんとまとめると下のような感じです。

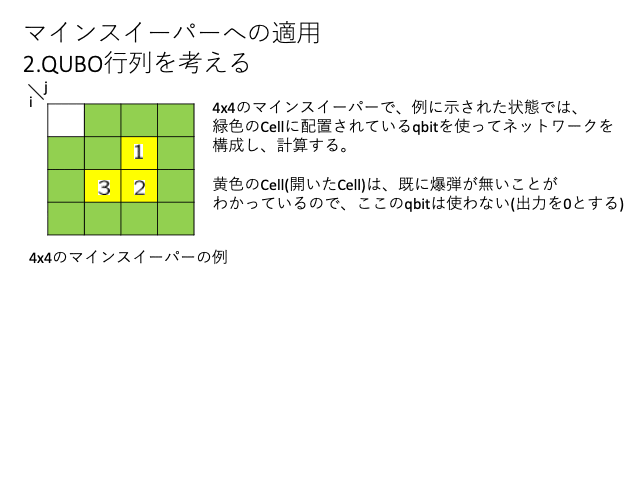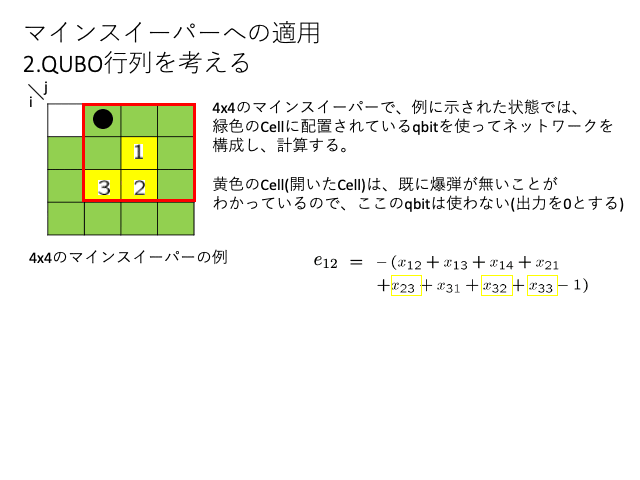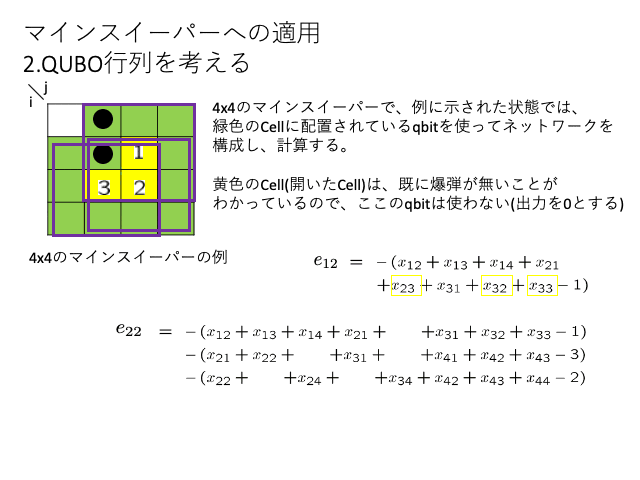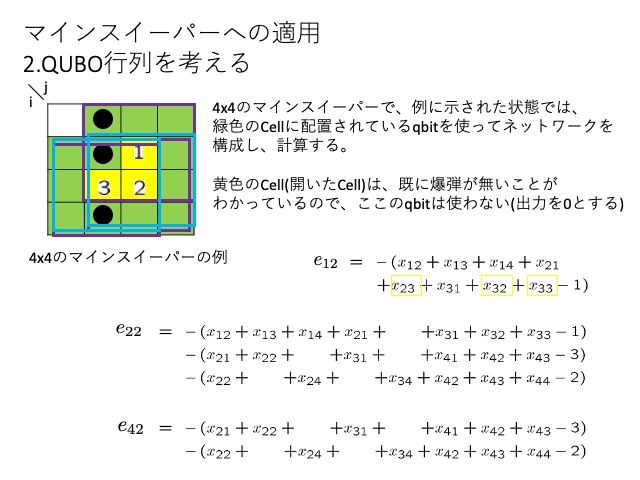
QUBO行列

QUBO行列は、i番目のqbitからj番目のqbitへの関係を表す行列です。

マインスイーパでは、ヒントの数字を介して関係しているqbitとの接続を考える。
考え方のスライドを作ったので下記に示します。

i番目のqbitに着目して、隣接Cellにヒントの数字があるか調べる、そのヒントの数字Cellに隣接のCellをj番目のqbitとする。

エネルギーのEの式を展開して、

*i != jの時は Q[i][j] += lam
*i == jの時は Q[i][j] += lam - 2 * lam * (ヒントの数字)

となります。
あとはひたすらコーディグするだけ。。。

#ソースコード
コードの解説なしでいきなり全部載せてしまってます。
マインスイーパのコードと量子アニーリングのコード合わせたものになっています。

D-Waveではなく、OpenJIJを有効しています。
（D-Waveだと一瞬で無料枠の1分使い切りそうでした。。。）

D-Waveに投げたい人は、コメントにしている、token, endpoint, samplerを有効して試してください。

minesweeper-qa.py

import sys
import numpy as np
import random
#from dwave.system import DWaveCliqueSampler
from openjij import SQASampler

#token = '***' # 自分のAPI-keyを入れる
#endpoint = 'https://cloud.dwavesys.com/sapi/'
Nsample = 100 # 量子コンピュータで解く回数 Dwave使うときは10くらいにした方がいいです
lam = 1.0     # QUBO行列のハイパーパラメータ


## マインスイーパの設定
M = 10                # 横のCellの数
N = 10                # 縦のCellの数
nMines = 25           # Number of mines


openFlagArray = np.zeros((M, N))    # 開かれているCellのフラグ, 0:not open, 1:open
mineArray = np.zeros((M, N))        # 爆弾の入っているCell, 0:not mine, 1:mine
mineNumArray = np.zeros((M, N))     # 周囲の爆弾の数を格納するArray


### minesweeper用の部品 ###
# 盤面表示関数
def printBoard(openFlagArray, mineArray, mineNumArray):

  print("    ",end="")
  for i in range(M):
    print("{0:>2d}".format(i),end="")
  print("")

  for j in range(N):
    print("{0:4d}".format(j),end="")
    for i in range(M):
      if(openFlagArray[i][j] == 0):
        print("| ",end="")
      else:
        if(mineArray[i][j] == 1):
          print("|*",end="")            ## 爆弾のCellは*
        elif(mineNumArray[i][j] == 0):
          print("|-",end="")            ## 0のCellは-
        else:
          print("|{0:1d}".format(int(mineNumArray[i][j])),end="")
    print("|")


# 解答表示関数
def printAnswer(mineArray, mineNumArray):

  print("    ",end="")
  for i in range(M):
    print("{0:>2d}".format(i),end="")
  print("")

  for j in range(N):
    print("{0:4d}".format(j),end="")
    for i in range(M):
      if(mineArray[i][j] == 1):
        print("|*",end="")            ## 爆弾のCellは*
      elif(mineNumArray[i][j] == 0):
        print("|-",end="")            ## 0のCellは-
      else:
        print("|{0:1d}".format(int(mineNumArray[i][j])),end="")
    print("|")


# Cellを開く関数、ゼロ(周囲 8 Cellに爆弾なし)のCellは自動で開く
def openCell(ox, oy, openFlagArray, mineArray, mineNumArray):

  if (ox < M and oy < N and ox >= 0 and oy >= 0):     ## 問題サイズ内か判定
    openFlagArray[ox][oy] = 1                         ## 対象のCellの開封フラグを1に変更

    if (mineNumArray[ox][oy] == 0):
      for i in range(-1, 2):
        for j in range(-1, 2):
          if ( (ox + i) < M and (oy + j) < N and (ox + i) >= 0 and (oy + j) >= 0 ):
            if ( openFlagArray[ox+i][oy+j] == 0 and mineNumArray[ox+i][oy+j] == 0 and mineArray[ox+i][oy+j] == 0 ):
              openCell(ox+i, oy+j, openFlagArray, mineArray, mineNumArray)
            openFlagArray[ox+i][oy+j] = 1
  else:                                               ## 問題サイズ外のエラー処理
    print("out of range X, Y")


# GAMEの終了判定
def endJudgment(ox, oy, openFlagArray, mineArray, mineNumArray):
  endFlag = 0
  numOpenCells = M * N
  if(mineArray[ox][oy] == 1):
    print("### GAME OVER! ###")
    printAnswer(mineArray, mineNumArray)
    endFlag = 1

  for i in range(M):
    for j in range(N):
      if(openFlagArray[i][j] == 1):
        numOpenCells -= 1

  if (numOpenCells == nMines):
    print("GAME CLEAR!!!")
    endFlag = 1

  return endFlag

### minesweeperの部品ここまで ###



### QA solver ### 
### mineArray は爆弾の位置が入っているので使用禁止!!! ###
### mineNumArrayはopenFlagArray[i][j] = 1の部分のみ使用可!!! ###
def qa_solver(openFlagArray, mineNumArray):

  # 探索するCellの選択, ヒントの数字の周りの部分を対象とする
  qFlag = np.zeros((M,N))
  for i in range(M):
    for j in range(N):

      if (openFlagArray[i][j] == 1):

        for k in range(-1, 2):
          for l in range(-1, 2):
            if ( i + k >= 0 and i + k < M and j + l >= 0 and j + l < N ):
              if( openFlagArray[i + k][j + l] == 0 ):
                qFlag[i+k][j+l] = 1


  # qbitの番号とminesweeprのcellの変換表作る
  numQbit = int(sum(map(sum, qFlag)))
  print( "num of qbit = {0:d}".format(numQbit) )

  qList = np.zeros((M,N), dtype=int)
  qList[:][:] = -1
  qAddr = np.zeros((int(numQbit),2), dtype=int)
  k = 0
  for i in range(M):
    for j in range(N):
      if (qFlag[i][j] == 1):
        qList[i][j] = k
        qAddr[k] = [i, j]
        k += 1

  # 頑張ってスパースなQUBO行列作る 
  QUBO = np.zeros((numQbit,numQbit))
  for i in range(numQbit):

    # i 番目のcellの周囲8cell探索してヒントの数字cellを見つける
    for k in range(-1, 2):
      for l in range(-1, 2):
        if (qAddr[i][0] + k >= 0 and qAddr[i][0] + k < M and qAddr[i][1] + l >= 0 and qAddr[i][1] + l < N):
          if (openFlagArray[qAddr[i][0]+k][qAddr[i][1]+l] == 1 ):

            # 数字cellの周囲8cellで開いていないcellと結合を持つ
            for m in range(-1, 2):
              for n in range(-1, 2):
                if (qAddr[i][0]+k+m >= 0 and qAddr[i][0]+k+m < M and qAddr[i][1]+l+n >= 0 and qAddr[i][1]+l+n < N):
                  if (qFlag[qAddr[i][0]+k+m][qAddr[i][1]+l+n] == 1):
                    if( i == qList[qAddr[i][0]+k+m][qAddr[i][1]+l+n] ):
                      QUBO[(i,qList[qAddr[i][0]+k+m][qAddr[i][1]+l+n])] += lam - 2 * lam * mineNumArray[qAddr[i][0]+k][qAddr[i][1]+l]
                    else:
                      QUBO[(i,qList[qAddr[i][0]+k+m][qAddr[i][1]+l+n])] += lam

  # 辞書に変換
  Qdict = {}
  for i in range(numQbit):
    for j in range(numQbit):
      if QUBO[i][j] != 0.0:
        Qdict[(i,j)] = QUBO[i][j]


  # openjijで解いてみる
  #sampler = DWaveCliqueSampler(solver='DW_2000Q_6', token=token, endpoint=endpoint)  # d-waveマシンに投げるとき
  sampler = SQASampler(num_sweeps = 1000) # openjij
  sampleset = sampler.sample_qubo(Qdict, num_reads=Nsample)


  # Nsampleの平均で爆弾の存在確率っぽく出力する
  x = np.zeros(Nsample*numQbit).reshape(Nsample,numQbit)
  for k in range(len(sampleset.record)):
    x[k,:] = sampleset.record[k][0]

  prob = np.average(x, axis=0)

  print(" x y  probability(mine)")
  for k in range(numQbit):
    print(qAddr[k],prob[k])

### end qa_solver ###


# ========== main routine ========== #
# 初手の入力
printBoard(openFlagArray, mineArray, mineNumArray)
print("input open cell (x y) =>  ",end="")
inXY = list(map(int, input().split()))


# 爆弾の初期配置
i = 0
while i < nMines:
  x = random.randrange(M)
  y = random.randrange(N)
  # 既に爆弾が配置済み及び初手のCellには爆弾を配置しない
  if (mineArray[x][y] == 0 or not(x == inXY[0] and y == inXY[1])):
    mineArray[x][y] = 1
    mineNumArray[x][y] = -1    # 爆弾の数の表,例外判定のため-1
    i = i + 1


# i, j Cellの周囲8 Cellにある爆弾の数を計算
for i in range(M):
  for j in range(N):

    if (mineArray[i][j] != 1):

      for k in range(-1, 2):          ## i,j Cellの周囲8 Cellの探索
        for l in range(-1, 2):
          if ( i + k >= 0 and i + k < M and j + l >= 0 and j + l < N ):
            mineNumArray[i][j] += mineArray[i+k][j+l]

openCell(inXY[0], inXY[1], openFlagArray, mineArray, mineNumArray)
printBoard(openFlagArray, mineArray, mineNumArray)

## ゲーム終わりまで再起実行
fin = 0
while(fin!=1):

  qa_solver(openFlagArray, mineNumArray)

  print("input open cell (x y) =>  ",end="")
  inXY = list(map(int, input().split()))

  openCell(inXY[0], inXY[1], openFlagArray, mineArray, mineNumArray)
  printBoard(openFlagArray, mineArray, mineNumArray)
  fin = endJudgment(inXY[0], inXY[1], openFlagArray, mineArray, mineNumArray)

実際解いてみた様子

ヒントの隣接Cellの爆弾がありそうな確率を出力する

テキストベースで格好悪いですが、こんな感じで動きます
（誰か格好いいインターフェイス作って。。）

     0 1 2 3 4 5 6 7 8 9
   0| | | | | | | | | | |
   1| | | | | | | | | | |
   2| | | | | | | | | | |
   3| | | | | | | | | | |
   4| | | | | | | | | | |
   5| | | | | | | | | | |
   6| | | | | | | | | | |
   7| | | | | | | | | | |
   8| | | | | | | | | | |
   9| | | | | | | | | | |
input open cell (x y) =>  3 4
     0 1 2 3 4 5 6 7 8 9
   0| | | | | | | | | | |
   1| | | | | | | | | | |
   2| | | | | | | | | | |
   3| | | | | | | | | | |
   4| | | |4| | | | | | |
   5| | | | | | | | | | |
   6| | | | | | | | | | |
   7| | | | | | | | | | |
   8| | | | | | | | | | |
   9| | | | | | | | | | |
num of qbit = 8
 x y  probability(mine)
[2 3] 0.53
[2 4] 0.56
[2 5] 0.56
[3 3] 0.47
[3 5] 0.45
[4 3] 0.55
[4 4] 0.51
[4 5] 0.37

[2 3] 0.53とありますが、2 3のcellの爆弾が入っていそうか度合いを出力しています。
量子アニーリングで100回サンプリングしていて、その平均を確率っぽく出しています。
同じ条件でも量子ビットの機嫌で答えが毎回変わります。

この数字を元に爆弾の確率が少ないCellを開いていけばクリアできるかも？

失敗もある

マインスイーパ自体が確率的なので、普通に失敗する時もあります。

input open cell (x y) =>  4 5
     0 1 2 3 4 5 6 7 8 9
   0| | | | | | | | | | |
   1| | | | | | | | | | |
   2| | | | | | | | | | |
   3| | | | | | | | | | |
   4| | | |4| | | | | | |
   5| | | | |3| | | | | |
   6| | | | | | | | | | |
   7| | | | | | | | | | |
   8| | | | | | | | | | |
   9| | | | | | | | | | |
num of qbit = 12
 x y  probability(mine)
[2 3] 0.57
[2 4] 0.68
[2 5] 0.52
[3 3] 0.61
[3 5] 0.47
[3 6] 0.43
[4 3] 0.64
[4 4] 0.5
[4 6] 0.42
[5 4] 0.42
[5 5] 0.34
[5 6] 0.42
input open cell (x y) =>  5 5
     0 1 2 3 4 5 6 7 8 9
   0| | | | | | | | | | |
   1| | | | | | | | | | |
   2| | | | | | | | | | |
   3| | | | | | | | | | |
   4| | | |4| | | | | | |
   5| | | | |3|*| | | | |
   6| | | | | | | | | | |
   7| | | | | | | | | | |
   8| | | | | | | | | | |
   9| | | | | | | | | | |
### GAME OVER! ###

ヒントの情報量が多くなるといい感じになってくる

ヒントの数字によって一意に爆弾の位置が特定できる場合は、ちゃんとサンプリング100回とも1 or 0を出してくれるようになる。

     0 1 2 3 4 5 6 7 8 9
   0| | | | | | | | | | |
   1| | | | | | | |1|1|1|
   2| | | | |2|2|1|1|-|-|
   3| | |2|1|1|-|-|-|-|-|
   4| | |1|-|-|-|-|-|-|-|
   5| | |3|1|1|-|-|1|2|2|
   6| | | | |2|1|1|2| | |
   7| | | | | | | | | | |
   8| | | | | | | | | | |
   9| | | | | | | | | | |
num of qbit = 25
(25,)
 x y  probability(QA)
[1 2] 0.48
[1 3] 0.01
[1 4] 0.49
[1 5] 0.5
[1 6] 0.96
[2 2] 0.02
[2 6] 0.02
[3 1] 0.03
[3 2] 0.99
[3 6] 1.0
[3 7] 0.33
[4 1] 0.96
[4 7] 0.38
[5 1] 0.03
[5 7] 0.28
[6 0] 0.01
[6 1] 1.0
[6 7] 0.32
[7 0] 0.0
[7 7] 0.4
[8 0] 0.02
[8 6] 1.0
[8 7] 0.28
[9 0] 0.98
[9 6] 1.0

おわりに

量子アニーリングは、たくさんある条件を一気に最適化するのに強いということで、マインスイーパもできそう、でやってみました。
実際やってみてQUBO行列の作り方が大事だと実感しました。forループの数がとんでもないことに・・・
組合せ最適化としてはマインスイーパは次に開ける1マスを選ぶだけなので割と簡単な部類なのかもとも思います。