この記事は「マイクロマウス Advent Calendar 2022」の7日目です。制御編は12日目に登録予定です。
はじめに
一般に、ロボットのモータ電流制御は、回路発熱の観点から電流ON/OFFで可変させます。特に、周波数は固定でパルスの幅が変えるPWM(Pulse Width Modulation)が良く用いられますが、回路の設計次第では制御性が悪化したり最悪モータが燃えたりします。
この知識は、モータ駆動回路を自分で組む場合だけでなく、ICやモジュールを使う場合でもその選定には必要な情報です。
ドライバ回路のスイッチング方式
モータの電圧・電流がPWMのDuty比(ON/OFFの比)に比例しないと、PID制御の精度や応答性の悪化に繋がる可能性が高いです。
モータ駆動回路でよく使われる以下の回路は、実は非線形であることが知られています。

これは、ON時間では$I_{MON}$が流れモータが加速するのに対し、OFF時間では$I_{MOFF}$が流れず、摩擦などに任せて成り行きで減速することが原因です。PWMではON時間では加速、OFF時間では減速することを前提としているので、一切摩擦がないような極端な例ではDuty比に関わらず$V_P$で駆動した場合と同じ回転数になってしまうでしょう。
次のようなスイッチングパターンのフルブリッジ回路も同様の理由で非線形になります。

対策としては、モータOFFの時間でも電流が流れるようにします。下図の回路ではM1とM2はお互いに逆のタイミングでスイッチングし、両方ともOFFの瞬間が発生しないようになっています(デッドタイムは非線形性の元)。これを同期整流といいます。

フルブリッジの場合はM1とM2もしくはM3とM4の組み合わせで交互にスイッチングさせて同期整流とします。
(Sign-Magnitude-Break方式と言われます)

例として東芝製2chモータドライバICTB6612FNGのPWMはこの方式を採用しています。

他にもM1~M4をすべてスイッチングしてしまう方法もあります。この場合はDuty=50%でモータが停止します。Locked Anti-Phase方式と言われる方式で、正負のトルクを切り替えなしに生成できる上に、ゲートドライバとPWM生成回路の間の信号線が少なくてすみます(ゲートドライバがデッドタイム生成可能な場合は1本だけ)。
一方で、PWMの分解能が半分になってしまう欠点があります。また、マイコン停止時に勝手に回ってしまわないような対策も必要です。

スイッチング周波の設計
もしPWMのスイッチング周期が1年だったら電流や電圧が調整できてるとは言えないでしょう。
PWMのスイッチング周期は負荷の応答速度との関係を考慮してで決めなければなりません。
電気的時定数と機械的時定数
モータは、コイルに流れた電流を電磁気力(フレミングの左手の法則)でトルクに変換します。コイルはインダクタンス$L$と巻線抵抗$R$の成分を持ちます。これは典型的なLRの1次遅れ回路で、電流の応答は以下のとおりです。$V_P$は電源電圧、$i_m$はコイル電流です。
(電気的な応答なので回転数変化は無視しています)
i_m(t) = \frac{V_P}{R} e^{-\frac{t}{\tau_e}} \\
\tau_e = \frac{L}{R}
$\tau_e$はモータの電流応答を決めるパラメータで電気的時定数といいます。
また、コイルに流れる電流はコイルと界磁で発生する逆起電力(フレミングの右手の法則)で妨げられます。トルクはコイル電流に比例するので、(モータ電圧が一定の場合)回転数の増加は次第に収束します。式で表すと次のように表せます。
(電源電圧$V_P$、回転数$n$[rpm]、$K_V$は回転定数[rpm/V]です)
n(t) = V_PK_V(1 - e^{-\frac{t}{\tau_m}})
このとき、$\tau_m$は機械的時定数です。
電流不連続モード
下図は、スイッチング周期を機械的時定数より短く、電気的時定数より長くした場合の電流波形で、電流不連続モードといいます。文字通り電流が途切れる瞬間が存在します。
電気的時定数よりスイッチング周期が十分に長いので電流と電圧パルスの形状がほぼ一致したパルス状になっている一方、機械的時定数よりは十分短いので回転数はあまり変動しません。
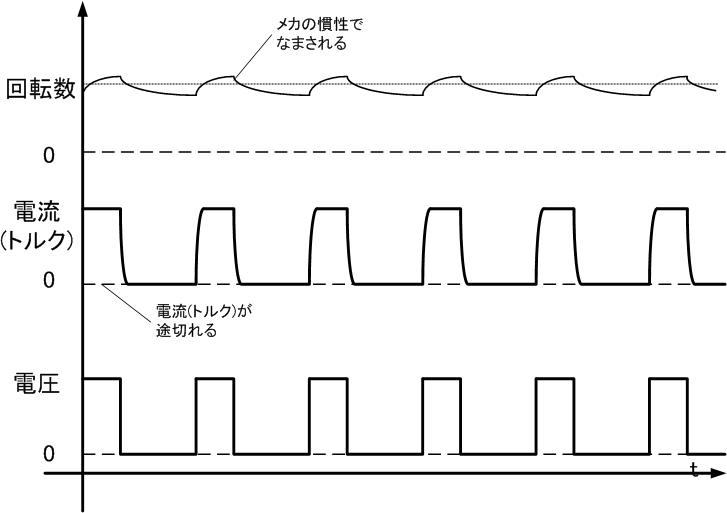
Dutyが小さくてもトルクのピーク値が大きいので、静止摩擦係数が大きい場合に有効ですが、同期整流しようとすると発熱が大きくなりがちです(後述)。スイッチング周波数は比較的適当(数十Hz~数kHz程度?)で、振動が気にならない程度に下げておくのがセオリーです(もちろん、スイッチングがあまりに遅いと、制御の離散化が酷くなるので、制御対象次第です。)
(身近な例ではラジコンや電動工具が採用しています。Dutyを絞ると独特の音と振動が出るのでよく分かるはずです)
電流連続モード
下図は、電気的時定数より短いスイッチング周期を採用した場合です。電流が連続的に変化するので電流連続モードといいます。

同期整流との組み合わせでDutyの線形性性が良いのが特徴となります。しかし、高速なスイッチング周波数が必要とされ、設計が難しくなります。周波数の選定は考慮すべき項目がそれなりにあるので一つ一つ確認します。
スイッチング周波数の選定
電気的時定数
電流連続モードですので、電気的時定数がキーになります。
FAULHABER製 1717-006SRを例にすると、インダクタンスが65uHでコイル抵抗が4.3Ωですので、$\tau_e = L/R = 15.1[\mu s]$となります。
したがって、66[kHz]以上必要と計算できます。
モータの発熱
時定数より小さければOKかというとそうではありません。トルクが変動して振動につながるのはもちろんですが、異常発熱に繋がります。
簡単のために、理想的なモータが無負荷の状態での電流波形を示します。つまり平均電流はゼロです。

この図から分かる通り、周波数を変えても平均電流はゼロのままであるにも関わらず、周波数が低いほうが振幅と実効値が大きくなります。交流での抵抗の発熱は平均電力ではなく実効電力で決まるので、周波数が低いPWMの場合は発熱が大きくなってしまいます。
(付け加えるなら、電流不連続モードで同期整流をしてはいけない理由でもあります)
感覚的には最低3倍。推奨10倍ほしいです。
(稼働時間が短いとか信頼性がそこまでいらないとかであればそんなに気にしないのもアリですが。。。。)
なお、先に例としてあげたモータ(FAULHABER製1717)では、3倍で198kHz。10倍で660kHzとなるので、駆動回路の設計は相当に困難です(10倍の場合、おそらく実現可能なモータドライバICはほとんど無いと思います)。
その場合は、モータに直列のインダクタを入れることで電気的時定数を大きくすれば良いでしょう。(↓のコイルを入れた場合は、$\tau_e$が66μs。PWM周波数は10倍で150kHzとなり現実的です)

インダクタンス入れるなら、コイルの定格電流は(ワリと真面目1に)守りましょう。飽和してしまい、入れた意味なくなるので。。。2

スイッチング損失
スイッチング素子は理想的には損失が発生しませんが、実際のMOSFET等はON⇔OFFの遷移途中で損失が発生します(素子にかかる電圧、流れる電流Iのどちらかが0とならない中途半端な状態が存在し、V*Iが0にならないので)。
スイッチング周波数が上がれば秒あたりのスイッチング回数が増え、発熱(ワット)が増えるのでむやみに周波数を上げることは出来ません。
デッドタイム
同期整流では上下の素子が同時にONするとショートしてしまいます。しかも、実際は素子のスイッチング遅れがあるので、M1とM2の切り替えを同時3に行った場合でも流れてしまいます。このとき流れるスパイク状の電流を貫通電流といいます。

そこで、両方ともOFFする時間を設けるデッドタイムが必要となります。

このデッドタイムは素子の遅延時間から決めるので固定時間となるので、スイッチング周波数が高速になればなるほどデッドタイムがOFFする時間が無視できなくなり、使用可能なDuty比範囲が狭くなってしまいます。
(例:デッドタイム=1usの場合、PWM周波数100kHz(10μs周期)の場合、Dutyを10%以下(もしくは90%以上)に設定しても片側のスイッチがONできなくなる)
クロック
マイコンでPWMを生成する場合はクロックのエッジ回数を数えてH/L出力します。したがって、PWM周波数がクロックに近づくとPWMの分解能が減少します。

(分解能100の場合)

(周波数が上がり分解能4の場合)
PID制御では、Dutyの分解能がある程度(感覚的に1000ぐらい?)は欲しいのでむやみにPWM周波数を上げることはできません。
(PWM回路への供給クロックを上げる方法もあるが、PWM回路はCPUに比べて低いクロックでないと動作しない場合が多いので限界がある。)
まとめ
- 同期整流を用いることでPWMの線形性が確保しやすい
- 同期整流を用いる場合は電流連続モードを採用する
- 電流連続モードのPWM周期は、電気的時定数より短くかつ各種設計の制限を考慮する
以上です。長々とお付き合いいただきありがとうございました!
参考
- TUTロボコン同好会-NOTE
- パワーMOS FETの高速スイッチング応用(ISBN-10 : 4789836088)