こんにちは。
この記事はLIFULL Advent Calendar 2022の3日目の記事です。
いきなりですが、競馬のオッズの表記をご存知でしょうか?
今回は「複勝とワイドだけなぜか1.3倍~2.4倍のようにレンジで曖昧に表記される件」について対抗していこうと思います。
前置き
競馬には単勝、複勝、枠連、馬単、馬連、ワイド、三連複、三連単の8種類の投票方法(買い方)があります。
投票方法ごとに何を予想すればいいのかは以下の通りです。
- 単勝: 1着の馬の馬番号を的中させる
- 複勝: 3着以内のいずれか1頭の馬番号を的中させる
- 枠連: 1着と2着になる馬の枠番号の組合せを的中させる
- 馬単: 1着と2着になる馬の馬番号を着順通りに的中させる
- 馬連: 1着と2着になる馬の馬番号の組合せを的中させる
- ワイド: 3着までに入る2頭の組合せを馬番号で的中させる
- 三連複: 1,2,3着までの馬の馬番号の組合せを的中させる
- 三連単: 1,2,3着までの馬の馬番号を着順通りに的中させる
この中で複勝とワイドでのみ、あたりになる馬券の組み合わせが1通りではないということです。
例えば、馬連は5番→10番→7番の順でレースが決まった場合、馬連5-10のみ的中となります。
しかし、ワイドだと5-7,5-10,7-10のいずれに投票していても的中となります。
複勝も同様に、5,7,10のいずれに投票しても的中となります。
簡単に4頭の競馬で複勝の払い戻しを考えてみます(4頭の場合は本当は複勝は発売されないし、7頭以下の場合は2着まで的中となりますが今回は3頭まで的中とします。)
1,2,3,4番の複勝の売上が1,2,3,6万円としましょう。
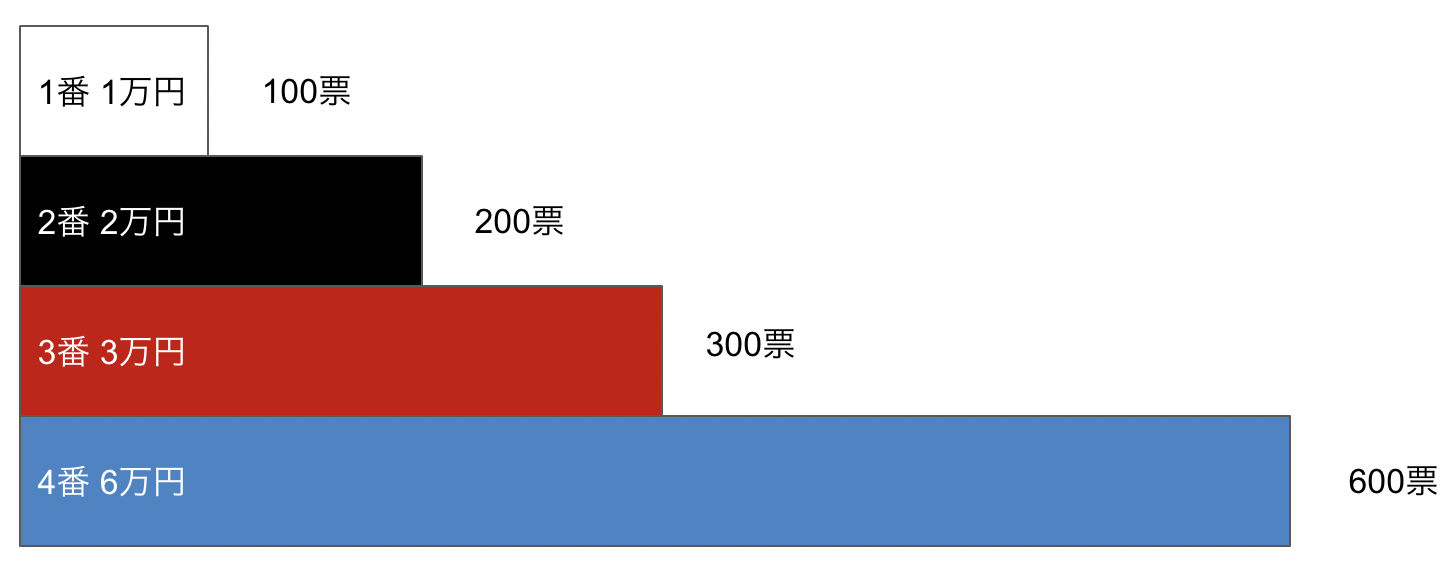
ここで、1,2,3の順番でレースが決まった時の1,2,3の複勝に投票した人の払い戻しは、
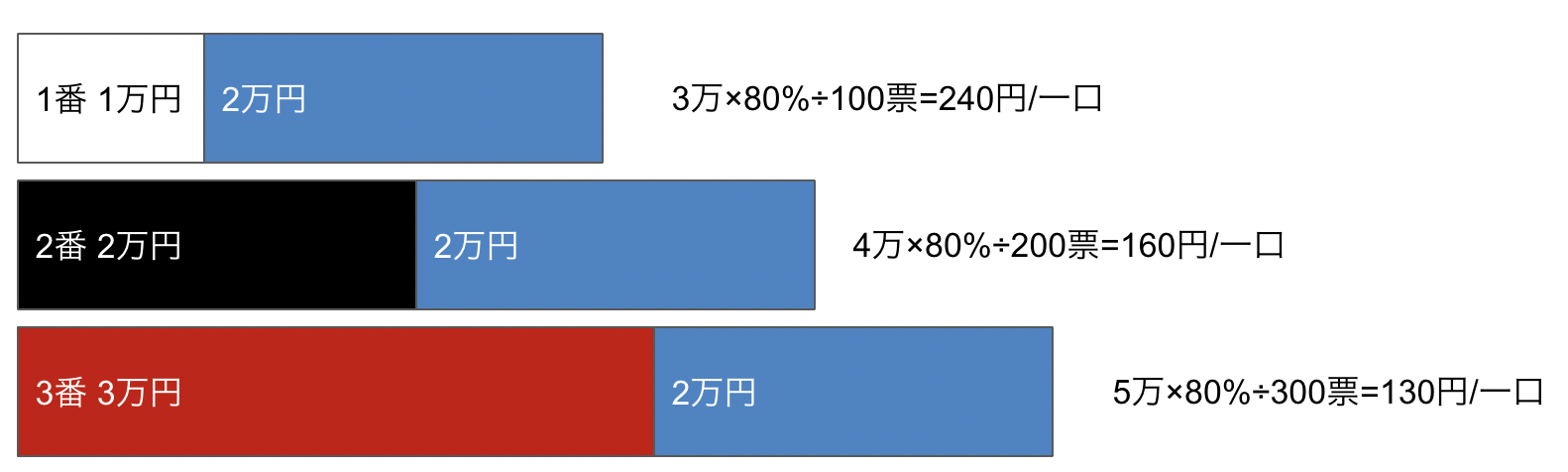
もう一例、1,2,4の順番でレースが決まった時の1,2,4の複勝に投票した人の払い戻しは、
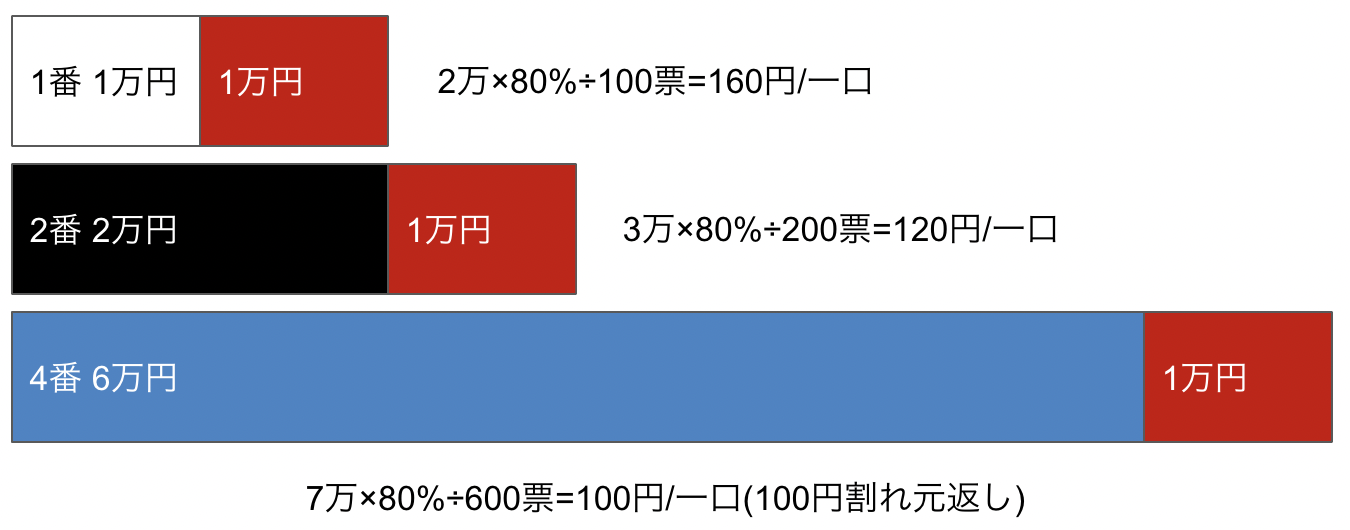
となり、人気馬が馬券に絡まない方が配当が良くなることがわかるし、どの馬が来るかによって同じ馬番1番に投票していても配当が異なることがわかります。
本題
冒頭の質問に戻って、複勝とワイドのオッズは1.3倍~2.4倍のようにレンジで表記されます。
理由は前置きに書いた通り、その馬券以外のどの馬が来るかによって配当が異なるためです。
しかし、前置きの例を使って、
- 複勝1番(残りは2,3番): 2.4倍
- 複勝1番(残りは2,4番): 1.6倍
- 複勝1番(残りは3,4番): 1.3倍
のように、残りの組み合わせを全列挙すれば詳細のオッズは表記可能です。
可能ですが、困ったことに簡単には教えてくれないのです。(例のように、各種投票数がわかっていれば計算できます。)
より正確な期待値計算のためには、正確に配当を計算できる必要があります。
期待値は-30円~+50円(分布不明)だと困るのです。
ですので、今回は1.3倍~2.4倍のようなレンジの表記から詳細のオッズを概算する方法を考えてみます。
方針
実際にあった8頭立てのレースの複勝のオッズを持ってきました。
- 1番: 6.4-30.0
- 2番: 2.4-10.4
- 3番: 2.3-9.9
- 4番: 1.1-1.1
- 5番: 1.5-5.5
- 6番: 3.1-13.7
- 7番: 1.2-4.0
- 8番: 1.4-4.9
まず、何番が人気なのかはオッズを見ればわかります。
1番人気は4番、時点で7番
最下位人気は1番、時点で6番と言ったふうにオッズが低いほど人気で高いほど不人気です。
さらに、複勝2番: 2.4倍~10.4倍からわかることがあります。
2.4倍は最低値で、10.4倍は最高値であるということです。
つまり、2.4倍をつけるときは1番の馬以外の人気馬1位(4番)と2位(7番)が馬券に絡んできた時ということです。
逆に、10.4倍をつけるときは1番の馬以外の不人気馬1位(1番)と2位(6番)が馬券に絡んできた時ということです。
欲しかった詳細オッズの2つは判明しました!
- 複勝2番(残りは1,3): ?
- ...
- 複勝2番(残りは1,6): 10.4倍
- ...
- 複勝2番(残りは4,7): 2.4倍
- ...
- 複勝2番(残りは7,8): ?
オッズを求めるためには、各馬券の投票率が必要なので、$n$ 番の馬の投票率を $x_n$ とすると、
$$
\sum_{n=1}^N x_n = 1
$$
であり、これを使って「複勝2番(残りは1,6): 10.4倍」は
$$
\frac{0.8(x_2 + x_1 + x_6 + \frac{1}{3}\sum_{\backslash { 2,1,6 } }^{8}x_n)}{x_2}=10.4
$$
と表せます。(0.8は胴元が還元してくれる率。複勝の場合は80%,ワイドの場合は77.5%が基本)
すべての、馬券には少なくとも1票は投票されるとすると、
$$
3x_1 - 36x_2 + x_3 + x_4 + x_5 + 3x_6 + x_7 + x_8 = 0
$$
と変形できます。
また、「複勝2番(残りは4,7): 2.4倍」から
$$
x_1 - 6x_2 + x_3 + 3x_4 + x_5 + x_6 + 3x_7 + x_8 = 0
$$
を得ます。
一つのオッズから2個式が得られるので8頭x2=16式が得られ、投票率の制約条件から+1式の計17式。
未知変数は8個なので、答えが求まりそうな気がしますが...
実装
大学時代のかすかな記憶をたどり、ムーア・ペンローズの擬似逆行列とやらでこういう場合の解を求められたことを思い出して、pythonで実装してみました。
from collections import defaultdict
from itertools import combinations
import numpy as np
from numpy.linalg import pinv
def simulate_place(
odds: dict[int, tuple[float, float]], payout_rate: float = 0.8
) -> dict[int, dict[tuple[int, int], float]]:
"""複勝オッズの最小と最大のオッズから他をシミュレートする
擬似逆行列を用いた概算
オッズの少数第二位以降が切り捨てられるのと、1.0を割るオッズは元返しになるためあくまで概算となる
Args:
odds (list[dict[int, tuple[float, float]]]): 馬番ごとのオッズ(最小, 最大) {1: (2.4, 4.0), 2: (1.2, 1.7), ...}
Returns:
dict[int, dict[tuple[int, int], float]]: 複勝の買い目と相手ごとのオッズ
{
1: {(2, 3): 1.7, (2, 4): 1.8, ..., (7, 8): 1.1},
...,
8: {(1, 2): 1.1, ..., (6, 7): 1.1},
}
"""
N = len(odds)
pops = sorted(odds.items(), key=lambda x: x[1][0] + x[1][1])
matrix = []
n_selection: dict[int, dict[tuple[int, int], float]] = {}
for n, odds_min_max in odds.items():
# オッズの最小、最大になるのがどの着順の時なのか計算する
_ = [x[0] for x in pops if x[0] != n]
_min = (min(_[0], _[1]), max(_[0], _[1]))
_max = (min(_[-1], _[-2]), max(_[-1], _[-2]))
n_selection[n] = {_min: odds_min_max[0], _max: odds_min_max[1]}
# 最小、最大のオッズからそれぞれ連立方程式の係数を計算する
matrix.append(coefficient(N=N, selection=(n, *_min), odds=odds_min_max[0], payout_rate=payout_rate))
matrix.append(coefficient(N=N, selection=(n, *_max), odds=odds_min_max[1], payout_rate=payout_rate))
# 0じゃない解が欲しいので制約をいれる
matrix.append([1.0 for _ in range(N)])
A = np.array(matrix)
b = np.array([[0] for _ in range(N * 2)] + [[1]])
Inv_A = pinv(A)
votes = dict(zip(range(1, N + 1), (Inv_A @ b).reshape(-1).tolist()))
results: dict[int, dict[tuple[int, int], float]] = defaultdict(dict)
for i in votes.keys():
for comb in combinations((k for k in votes.keys() if i != k), 2):
v = place(votes, (i, *comb), payout_rate=payout_rate)
results[i][comb] = clip(v, *odds[i])
# 一応、元の情報のあるところは上書き
for i, values in n_selection.items():
for comb, odd in values.items():
results[i][comb] = odd
return dict(results)
def clip(x: float, a: float, b: float) -> float:
if x < a:
return a
elif b < x:
return b
return x
def coefficient(N: int, selection: tuple[int, int, int], odds: float, payout_rate: float = 0.8):
n = selection[0]
k_n = 3 * (odds / payout_rate - 1)
def c(i: int):
if i == n:
return -k_n
elif i in selection:
return 0.0
return 1.0
return [round(c(i), 5) for i in range(1, N + 1)]
def place(votes: dict[int, float], selection: tuple[int, int, int], payout_rate: float = 0.8):
target = selection[0]
total_votes = sum(votes.values())
selection_votes = sum(votes[i] for i in selection)
lost_votes = total_votes - selection_votes
return odd(votes[target], lost_votes, payout_rate=payout_rate)
def odd(target_votes: float, lost_votes: float, wins: int = 3, payout_rate: float = 0.8):
odds = (target_votes + lost_votes / wins) / target_votes
odds *= payout_rate # 控除
floor = int(odds * 10) / 10 # 少数第二位切り捨て
return max(1.0, floor) # 元返し保証
if __name__ == "__main__":
odds = [
(1, (6.4, 30.0)),
(2, (2.4, 10.4)),
(3, (2.3, 9.9)),
(4, (1.1, 1.1)),
(5, (1.5, 5.5)),
(6, (3.1, 13.7)),
(7, (1.2, 4.0)),
(8, (1.4, 4.9)),
]
print(simulate_place(odds=dict(odds)))
ちなみにこのレース、4->6->8の順で入賞しており、
複勝の払い戻しは、
- 4: 110円
- 6: 330円
- 8: 160円
で、スクリプトの実行結果の該当部分を見ると
- 4(6,8): 1.1倍
- 6(4,8): 3.5倍
- 8(4,6): 1.6倍
でした。
6番だけ20円ずれています。
これは4番のオッズが1.1~1.1となっており、おそらくJRAプラス10が発動してオッズの計算がうまく再現できなかったからだと思っています。
違うよ〜ってわかった方は教えていただければ嬉しいです。
また、ワイドも同じ感じで計算することができましたが省略させていただきます。
感想
今回は競馬の省略されている中間のオッズを計算で求めてみました。
そんなに難しいことはしてないのですが、競馬の細かい知識を調べたり、大学の時のこれいつ使うんだよ的な知識が使えて楽しかったです。
最後に...
今回のやり方はあくまで概算であることに注意してください。
というのも、オッズは少数第二位以下が切り捨てられたり、オッズが1を切った場合元返しになったり、JRAプラス10という謎のキャンペーンで元返しになるはずのところを1.1倍返しになったりならなかったり、JRAプレミアムなるキャンペーンで還元率が変動したりするので完璧には計算できなかったりします。