はじめに
アドベントカレンダーの一日目の記事です。
以下の内容はあくまで個人の見解であり、所属する企業・団体の見解を代表するものではございません。
ギャンブルと投資
カジノ、パチンコ、競馬、宝くじといったものはギャンブルに該当すると思う人は多いのではないでしょうか?
一方、長期買いの株式なんかは投資と呼ばれたりします。
違いは何でしょうか?
よく言われるのがギャンブルはマイナスサムゲームであり、投資はプラスサムゲームという違いです。
正確な定義は知りませんが私はマイナス・ゼロ・プラスサムゲームを以下のように認識しています。
「お金を拠出してから配当を回収する一連のゲームを行った後にゲーム参加者全員の利益の合計が0なのか以上なのか以下なのかというもの」
確かにギャンブルと言われるくくりのものは胴元が掛け金の一部を回収した後で参加者に分配するのでマイナスサムゲームになります。
一方株には配当があるので、全員が利益を出すことができます。
また、経済が拡大し株価がインフレし続ける限り、長期の売買でも利益を得ることができそうです。
しかし、株でも短期の売買ではゼロサム(手数料取られるから若干マイナス)になるので、ギャンブルと言えるかもしれません。
マイナス・ゼロ・プラスサムゲームで比較的、負けにくいのはプラスサムゲームでしょう。
しかし、負ける可能性はゼロではありません。
逆にマイナスサムゲームでも勝つことはできます。
ギャンブルと投資の違いに戻りますが、私は勝てるとわかってる(見込みが高い)ものにお金をかける行為を投資とよび、運任せのものにお金を賭ける行為をギャンブルと呼ぶと考えました。
では、一般にギャンブルと呼ばれるゲームで勝つ(投資にする)ことはできるのでしょうか?
マイナスサムゲーム攻略
マイナスサムゲームに勝つには、ただでさえ単純期待値マイナスの状況を引っくり返し、利益を得る必要があります。つまり、他の参加者と違うことを行い、より自分以外に損益を出させることが必要となります。
ということで以下が勝つため最低条件だと考えます。
- ギャンブルをしている参加者が多くいる
- 多数が不合理な選択をする熱狂性がある
- 他人と違う行動選択を取れる余地がある
- 自身の行動による結果の期待値が計算できる
一口にマイナスサムゲームといってもいろいろあります。上記を満たすゲームを探します。
例えば日本の宝くじは、50%以上胴元が持って行ってしまいます。
しかも、どこの券売所に買うかぐらいしか工夫の余地がないです。
参加者全員がほぼ同じ期待値で闘うことになるので勝ちようがありません。
つまり、最強の宝くじ攻略は購入しないことです。(参加者と違うことをする)
パチンコはどうでしょうか?
私は打ったことがないので詳しくは分かりませんが、
店や台など選択肢があり期待値計算などできるそうなので、うまくやれば勝てそうです。
うまくやってない人が大勢いそうなのもポイントです。
競馬や競艇などのオッズが参加者の投票で決まるものはどうでしょうか?
- 着順という不確実なものに対してロマンや謎の理論で賭けをする参加者が大勢いる
- オッズなどが公開されており、ある程度期待値が計算できる
ということでこれも条件を満たしてそうです。
また、オッズの仕組みも面白いため以降はこれのようなゲームで勝つ方法を掘り下げてきます。
オッズとは?
オッズとはゲームの結果が予測と一致した時に賭けた金額の何倍がもらえるのかを表す数字です。
これは計算式があり、
$$
\mathrm{オッズ} = \frac{還元率}{支持率}
$$
で計算できます。
還元率は胴元が掛け金から取り分をとった残りになる割合で、
支持率は対象に対してどれだけ掛け金全体に対してどれだけ掛けられているのかを表します。
例えばコイン投げで賭けを行い、還元率を90%(控除率10%)とすると、
| 対象 | 掛け金 | 支持率 | オッズ |
|---|---|---|---|
| 表 | 400 | 25% | 3.6倍 |
| 裏 | 1200 | 75% | 1.2倍 |
| 合計 | 1600 | 100% |
というように計算できます。
期待回収率
では先ほどのコイン投げゲームで勝つにはどうしたらいいのでしょう?
真のコインの確率を知ってれば1回収できる利益率の期待値(期待回収率)を計算することができます。
ここでいう期待回収率とは、全く同じオッズと確率のゲームをやり続けた時にかけた金額がその率倍に収束していくということです。
以下の例だと、100万を一回100で10000回表にかけた時、180万くらいになるということ。
つまり、期待値が100を超えるものに賭け続ければ局所的に負けることがあっても最終的には必ず勝てます。2
この状況下では必ず勝てるものにお金を払っているのでもはやギャンブルとは呼べないでしょう。
真の確率がわかることはそれだけの価値があるということです。
期待回収率は$オッズ\times対象の事象が起こる確率$で求められます。
| 対象 | 掛け金 | 支持率 | オッズ | 確率 | 期待回収率 |
|---|---|---|---|---|---|
| 表 | 400 | 25% | 3.6倍 | 50% | 180% |
| 裏 | 1200 | 75% | 1.2倍 | 50% | 60% |
たまたま、裏表50:50のコインなのに裏が連続で10回出ていた後だとこういうオッズになるかもしれませんね!
| 対象 | 掛け金 | 支持率 | オッズ | 確率 | 期待回収率 |
|---|---|---|---|---|---|
| 表 | 400 | 25% | 3.6倍 | 25% | 90% |
| 裏 | 1200 | 75% | 1.2倍 | 75% | 90% |
支持率と実際の確率が等しい場合です。
期待値が全て還元率と同じになってしまいました。
つまり、支持率と実際の事象の起こる確率に差があるときほど儲かるチャンスも生まれ、
逆に支持率と確率が近いほど参加者は誰も利益をあげられない3ということです。
これがマイナスサムゲーム最大の難点です。
このコイン投げゲームをやり続けて勝利者になるためには、
参加するゲームの見極めが重要となります。
期待回収率100%越えの世界
ではどういったゲームのとき期待回収率100%を超える賭け対象が現れるのでしょうか?
言い換えると、どれくらい真の確率と支持率が離れればいいのでしょうか?
軽く計算してみます。
同様にコイン投げの例で、真の確率を50%:50%/還元率が90%の場合は支持率の変化で回収率がどうなるのかを見てみます。
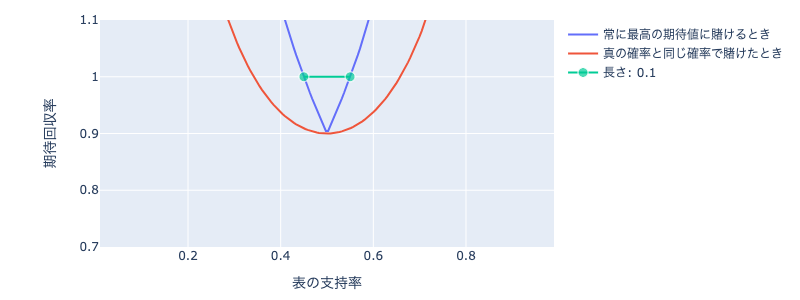
表の支持率を0~1で動かしてプロットしたものがこちらです。
(裏の支持率は1-表の支持率なので表だけで確率は決まる)
青線が表と裏の期待値の高い方に賭けた場合の回収率で、緑線はその時の回収率が1を超えない範囲を示しています。
この時の長さは0.1です。
つまり表の支持率が45%~55%より外側にあれば、胴元に控除される分を上回って利益を出せるということです。
(真の確率を知っているという強すぎる条件下であることに注意)
理想状態でも一定範囲ではどうやっても勝てない区間あることが分かりました。
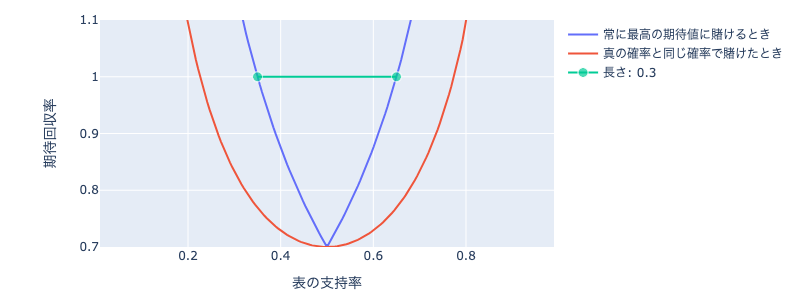
還元率を70%にしてみます。
緑線の長さが伸びてしまいました。これは100%以上の回収率を出すことが難しくなったことを表しています。
具体的にいうと表の支持率が35%~65%の間になるだけで誰も勝てなくなってしまいます。
還元率がゲームの難易度を上昇させることが分かりました。
ちなみに、コイン投げの場合の緑線の長さの計算式は
$$
(1 - 還元率 \times 裏の確率) - (還元率 \times 表の確率) = 1 - 還元率 = 控除率
$$
であることが分かります。
突然ですが、
$$
難易度=\frac{アンダー1の領域}{支持率が自由に動ける領域}
$$
と勝手に定義します。
コイン投げの場合は表の支持率は0~1までで変動できるのでそのうちの控除率分が常に勝てない領域となります。
なんだかコイン投げで30%も取られると勝てる気がしなくなりました。
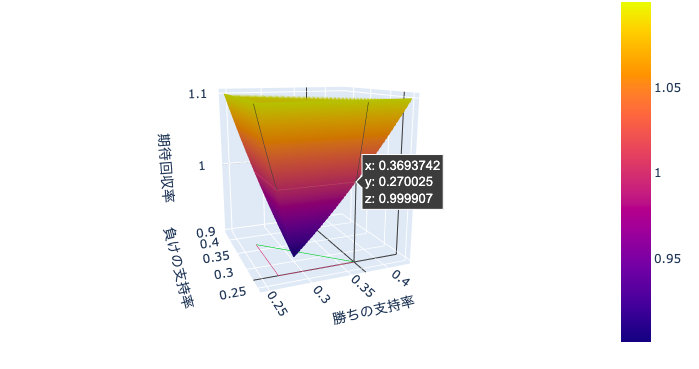
では、勝ち/負け/引き分けなどの三択を当てる賭けならどうでしょうか?
勝ちと負けの支持率の組み合わせで、期待値が1を超えるかどうかが決まります。
X,Y平面状にある、三角形の外側ならば1を超えるということを表しています。
この面積を計算してみます。
$$
\frac{1}{2} \times 控除率^2
$$
という式で計算できます。導出省略
勝ちと負けの支持率の動ける範囲の面積は$0.5$なので、三択の賭けの難易度は
$$
\frac{1}{2} \times 控除率^2 / 0.5 = 控除率^2
$$
となります。
ということで、還元率90%の場合難易度は1%となります。
証明はしてませんがおそらく、N択の難易度の算出式は
$$
控除率^N
$$
となるかと思われます。
つまり、 「賭ける対象が多いほど、難易度は低下する」 ということです。
朗報ですね。
競馬の単勝でいうと全馬の支持率を真の確率の±10%に収めないといけないということで、いかに集合知が素晴らしく支持率が優れていようとそんなことを毎回するのは不可能なので、よくよく考えれば、当然の気もします。
ここまででわかったことを整理すると
- 支持率次第で絶対に勝てない場合が存在する
- 控除率が勝ちやすさに関係している
- 選択肢が多い賭けほど勝てる余地が残りやすい
予測確率
ここまでの話は真の確率を知っている下で展開してきましたが、現実はそう甘くありません。
ですので、なんらかの手段で真の確率を予測した予測確率を求めることができたとしましょう。
コインの例に戻り考えてみます。
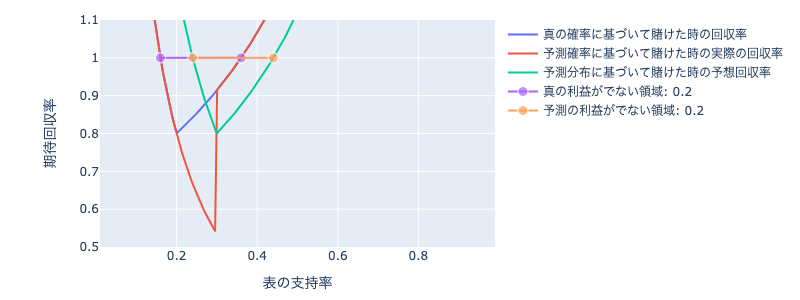
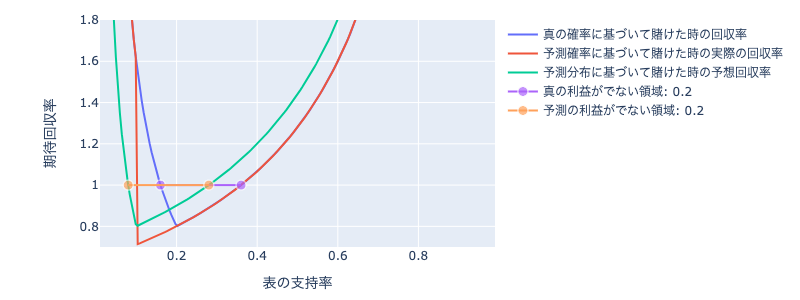
下の画像は、真の表の確率が0.2で予測の表の確率が0.3で還元率80%の時の期待回収率のプロットです。
つまり、表の確率を過大評価してしまった場合です。
紫線が先ほどと同様にどう足掻いても利益を出せない支持率の領域です。
オレンジ線は予想確率の下で利益がでない領域です。
予想と真の確率がずれているため、損益の領域もずれています。
自分の予想を信じる場合、支持率がオレンジ領域にあった場合はそのゲームを見送ることになります。
支持率が、紫の左端点とオレンジの左端点の間にあった場合のみ、損益を出すことになるのが分かります。
この幅は真の確率と予測確率のズレに等しいので、いかに予測の精度を上げるのかが大事かが分かります。
仮に予想の確率と真の確率のズレをある程度予想できるならば、ズレの可能性のある長さだけオレンジを前後に延長して参加するゲームを見極めればより安全になりそうです。
しかし、これは参加できるゲームが減ることを意味するので、資金を増やす機会が減ってしまうことに繋がります。
また、表の支持率が予測確率より過大評価されている場合は予測の回収率を過小評価してしまい、支持率が予想確率より過小評価している場合は予想の回収率を過大評価してしまいます。
表の確率を過小評価した場合は上記の逆です。
一般的なN択ゲームの場合は事象ごとに過大評価と過小評価が必ず混じるので、ある程度打ち消し合ったりしないかな?とか思っていますが、確認はしていません。
結論
- 勝てるとわかってるギャンブルは投資(独自論)
- 一回一回の勝ち負けを見るのではなく期待値を見ることが重要
- マイナスサムゲームは絶対勝てない場合がある
- なので参加するゲームの見極めが重要
- 見極めのためには予測確率分布が必要
- 精度次第では理論上ほぼ負けない
- なので参加するゲームの見極めが重要
- 場に流されるプレイヤーが多いゲームにはチャンスが多い
話としてはまだ終わっていなくて、理論と現実を隔てる問題として資金をどう投資するのかという話があります。
例えば、期待値プラスの方策が見つかり、その事象が起きる確率が1%だとすると、そんなものに全財産を投資するわけにはいきません。99%破産します。
つまり、破産せずかつ、資金を最大限早く増やす投資戦略を考えなければいけないということです。