※こちらの記事は"Pythonで学ぶあたらしい統計学の教科書"に基づいて、統計学初学者が頭の整理とアウトプットを目的に掲載している記事です。本の内容のみならず、自分で調べた内容、自分のイメージにマッチした内容を追記している場合もあります。
※今回はまだまだPythonを使用しません。
1. 確率質量関数
この関数について、参考書には下記のように記載されています。
データを引数にとると、確率が計算結果として出てくる関数のこと
つまり、ある関数$P(X=x)$に、$x = 1$を引数として与えます。この時に$P(X=1)$の結果は確率変数$X$が1となる確率となる関数を確率質量変数である、ということです。
具体的に例をあげて見ます。
サイコロを1回振ったときの出目がどの数字になるか、という試行においては、いずれの目も$\frac{1}{6}$になります。
この試行における確率質量関数が$P(X=x)$の時に、$x = 1$(サイコロの目が1となる)を与えると、$P(X=1)=\frac{1}{6}$となるということです。
補足
確率質量変数は、確率変数が"離散的な値"を必ず取ります。連続的な数値については、本記事の2.確率密度関数で説明します。
また、全ての確率変数に対する確率の総和は必ず"1"になります。上記のサイコロの場合、$X = 1,2,3,4,5,6$ですが、それぞれの確率変数を取る確率は$\frac{1}{6}$なので総和は1となります。
2. 確率密度関数
参考書に記載されていた確率密度関数の説明です。
データを引数に取ると、確率密度が計算結果として出てくる関数のこと
確率質量関数とは逆に、確率密度関数は連続的な確率変数を引数に取る関数です。
確率密度関数は引数を与えると確率密度を結果として返してくれます。
確率密度とは、連続的な確率変数の確率を表現するために使う表現方法の1つです。
確率密度関数に引数を与える場合は、$a_1 ≦ x < a_2$というような範囲で与えます。
変数は連続ですのでサイコロの目のように1つの値を与えても求められません。
例えば、180.0cmの人が何人いるのか、という時に小数点第2位まで精密に身長が測れるとします。
身長180.0cmの人を、精密に測ったら180.04cmだったという時、その人の身長は正確にいうと180.0cmではない訳です。
上記の場合、連続的な値(メートル,kgなどがその例でしょうか)を扱う際には、範囲で指定した方が良いということになります。
例えば、180.0cmの人がどれくらいいるのかという時には、$ 179.8 ≦ x < 180.2$というような具合でしょうか。そんなシチュエーションは基本的にはないですけれども!!
補足
確率質量関数では、全ての確率変数に対応する確率の総和は必ず1になると説明しました。
確率密度関数についても同様で、$-∞ < x < ∞$の範囲で総和が1となります。
確率密度関数$p(X=x)$を$-∞ < x < ∞$の範囲で積分することで求められます。
3. 正規分布
統計学1 - 統計学用語の理解 & 記述統計と推測統計
私の最初の記事で確率分布について、少し触れました。
確率分布の形にはいくつか種類があります。最も美しい形をした正規分布(ガウス分布)を見てみます。
正規分布(ガウス分布)
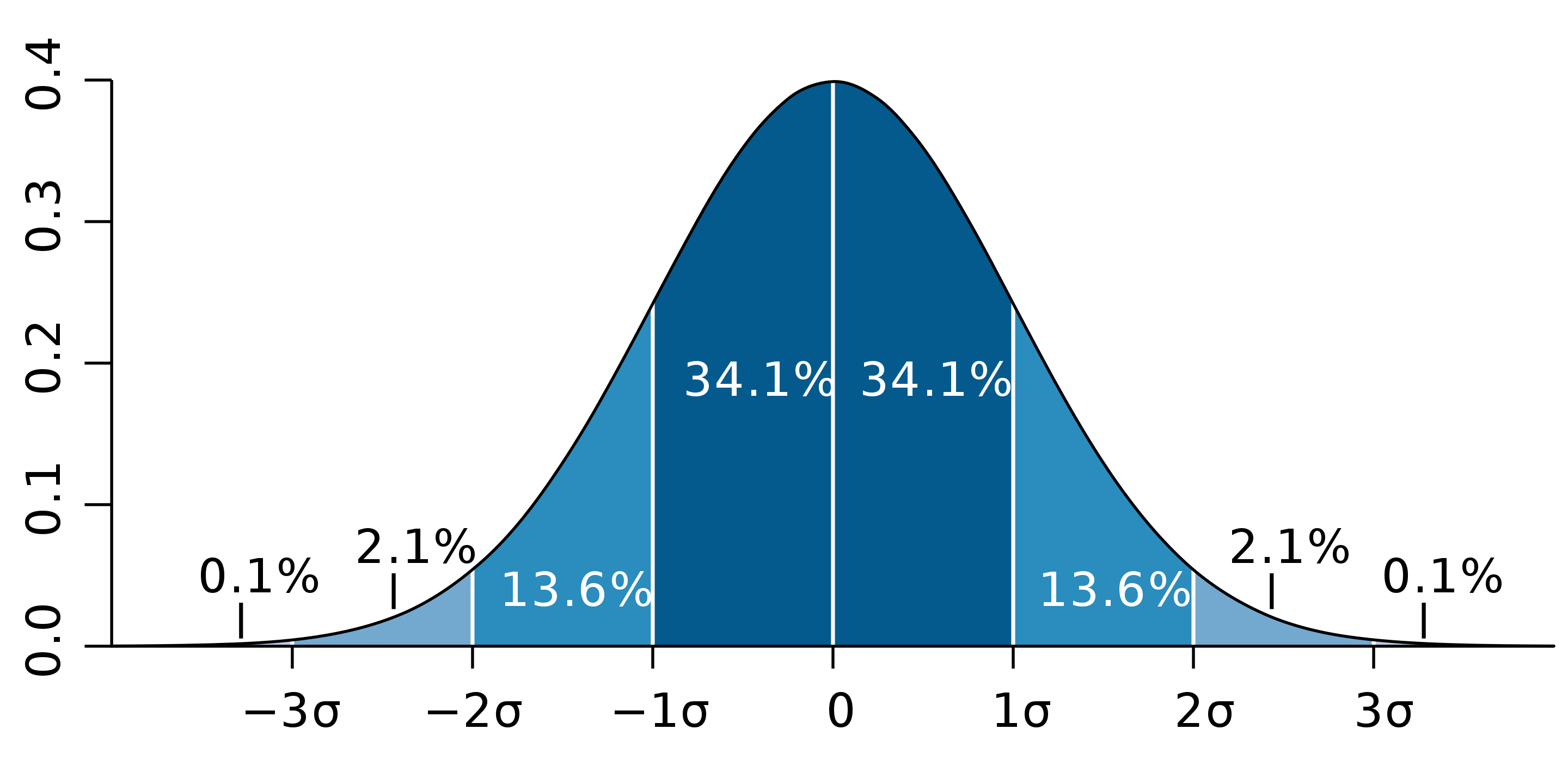
まず、正規分布の形を見てみましょう。
横軸や縦軸の意味についてはさておき、グラフの形に注目しましょう。
また、正規分布には下記の4点の特徴があげられます。
上記のグラフからイメージしてみてください。
- $-∞$ ~ $∞$の実数値を取る
- 平均値の付近の確率密度が大きい
- 平均値から離れるほど、確率密度が小さくなる
- 確率密度の大きさは平均値を中心として左右対称
出典:Pythonで学ぶあたらしい統計学の教科書
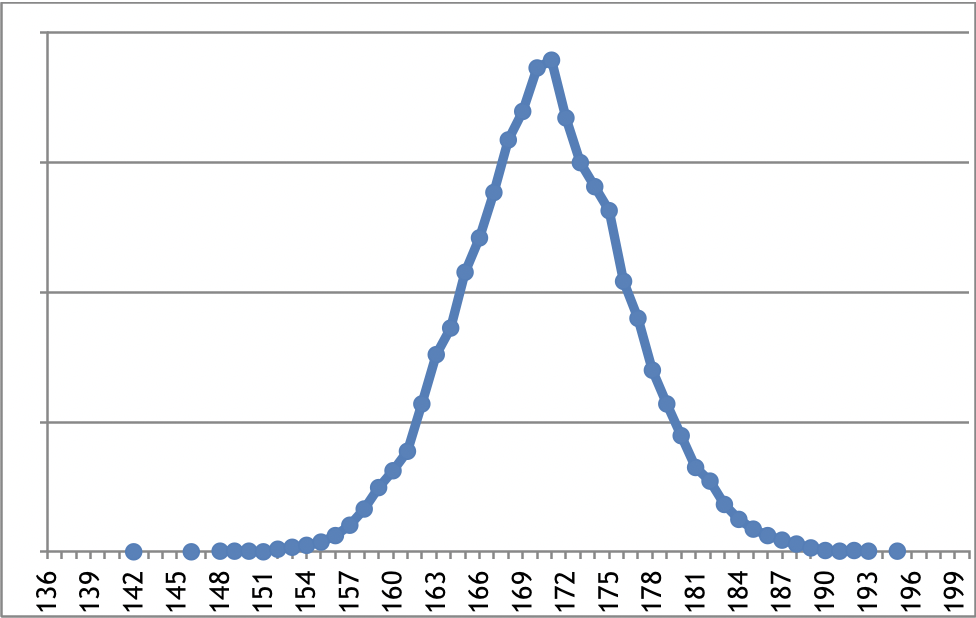
実際のグラフを見てみると分かりやすいかもしれません。
平成30年度の17歳男性の身長の分布は下記のようになっています。
下記のグラフを見ると先程あげた4点の特徴も分かりやすいですね。
また、正規分布は式で表すと下記のようになります。
$$ f(x) = \frac{1}{\sqrt{2\pi}\sigma}\exp(-\frac{(x-μ)^2}{2\sigma^2}) $$
14-1. 正規分布 - 統計WEB
分散$\sigma^2$,平均値$μ$は正規分布の形を特徴づけるパラメタ、母数といいます。
母数は「確率分布のパラメタ」です。
二項分布
二項分布(Binomial Distribution)とは、互いに独立したベルヌーイ試行をn回行ったときに、ある事象が何回起こるかの確率分布です。例えば、「コインを5回投げた時に表2回出る確率」「対戦ゲームで90%の確率で当たる技を10回中8回当てる確率」などを表した確率分布です。
(ベルヌーイ試行とは、試行結果が成功か失敗かの2通りしかない試行をさします。
参考:二項分布のわかりやすいまとめ - to-kei.net
ポアソン分布
ポアソン分布とは、(どの時点でも同様な起こりやすさでランダムに起こる現象と仮定した場合に)「単位時間あたりに平均 λ 回起こる現象が、単位時間に k 回起きる確率」を表すのに使われる確率分布のこと。
参考:ポアソン分布とは何か。その性質と使い方を例題から解説 【馬に蹴られて死ぬ兵士の数を予測した数式】 - アタリマエ!
まとめ
確率質量関数と確率密度関数という2つの種類の関数がありました。
離散的な値と連続的な値、どちらの確率変数を取るかによって関数も変わってくるのでした。
確率分布についてはいろんなパターンの確率分布があります。どの確率分布もパラメタ(確率分布の特徴を決定する値)があり、そのパラメタを求めることが重要です。
目的は、"母集団の分布を知ること"であり、パラメタを計算し特定することが今後必要になってきます。