※こちらの記事は"Pythonで学ぶあたらしい統計学の教科書"に基づいて、統計学初学者が頭の整理とアウトプットを目的に掲載している記事です。本の内容のみならず、自分で調べた内容、自分のイメージにマッチした内容を追記している場合もあります。
※今回はまだまだPythonを使用しません。
そもそも統計学とは
データの適切な取り扱い方を探る方法論を体系化した学問であると言えます。
統計学の中でもジャンルとして、2つに大きく分別されます。
- 記述統計 ・・・ 既知の手持ちデータの整理・要約する
- 推測統計 ・・・ 未知のデータを推測する
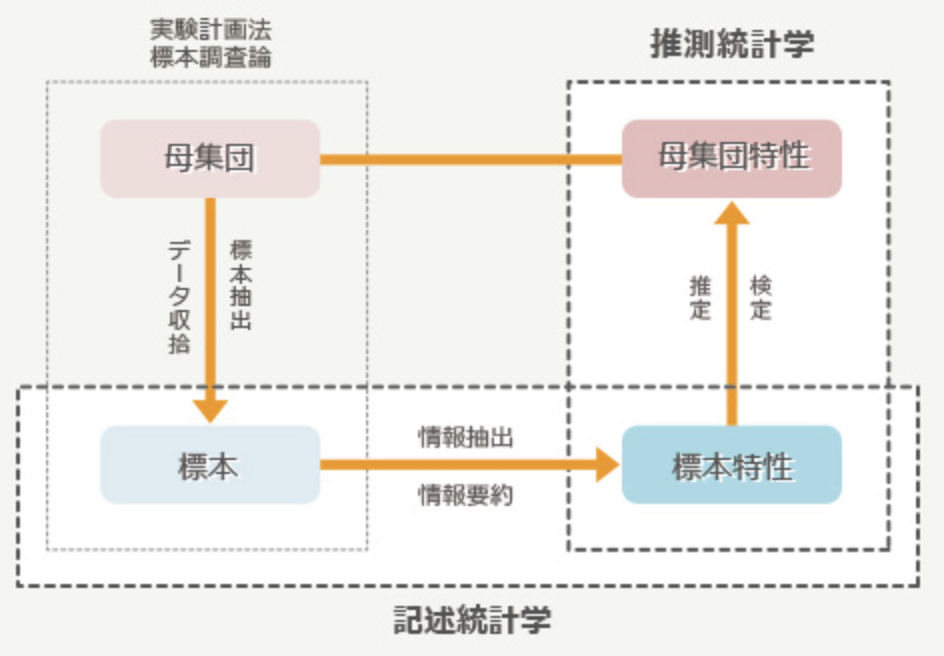
記述統計と推測統計の関係について、イメージ図がめちゃくちゃ分かりやすいのがあったので、下記画像見ればOK。
統計学の基礎用語
- 標本 ・・・ 手持ちの既知データ
- 母集団 ・・・ 未知のデータを含んだ、すべてのデータ
標本という母集団のごく一部のデータを用いて、母集団という全体について議論するということが推測統計の目的ということがこの段階でわかれば問題なし。
抽象化された標本を得るプロセス
用語
- 確率変数 ・・・ ある確率分布に従って変化する値
- 実現値 ・・・ 確率変数における具体的な値
- サンプリング ・・・ 母集団から標本を得ること、サンプリング = 標本抽出
- 単純ランダムサンプリング ・・・ 母集団から各要素がランダムでサンプリングする方法
- 確率分布 ・・・ 確率変数とそれに付与された確率との対応を表したもの
- 母集団分布 ・・・ 母集団が従う確率分布のこと
例 「小さな湖の中にいる魚を釣る」
話を簡潔にするために、下記の3つの前提条件を設定します。
- 母集団は、5匹の魚ですべて同じ種である。
- 5匹それぞれの大きさが2, 3, 4, 5, 6cmである。(小数点第1位を四捨五入)
- 釣った魚はすぐに湖の中にリリースする。
この湖の中で魚を1匹釣り、3cmの魚を釣ったと仮定します。5匹の中から3cmの魚1匹を釣っているので、確率としては、1/5となります。
このときの確率をP(2.5≦体長<3.4)=1/5という表記をします。
この式の意味は、体長が3cmの魚を釣れる確率は1/5であるという意味です。
体長は四捨五入するので、3cmの魚の場合は2.5cm以上、3.4cm以下の魚になります。
Pは、Probability(確率)の頭文字を表します。
このときの3cmの魚は実現値です。
また、次の釣りで釣る魚の大きさはどの大きさか分かりませんが、変数xという大きさの魚になります。この変数xを確率変数といいます。
この確率は、3cmの魚のみならず、他の魚を釣る場合も同じ確率となるので、下記のような確率分布となります。
P(1.5≦体長<2.4)=1/5
P(2.5≦体長<3.4)=1/5
P(3.5≦体長<4.4)=1/5
P(4.5≦体長<5.4)=1/5
P(5.5≦体長<6.4)=1/5
あるデータが、ある確率分布と対応している時、「確率分布に従う」という表現をします。
上記の例では、「釣れる魚の体長は、{1/5, 1/5, 1/5, 1/5, 1/5}の確率分布に従う」という表現になります。
母集団分布を通して、標本を得るプロセスを見直してみます。
① 以下の母集団から、単純ランダムサンプリングにより標本を1つ得る
1.5≦体長<2.4 : 1匹
2.5≦体長<3.4 : 1匹
3.5≦体長<4.4 : 1匹
4.5≦体長<5.4 : 1匹
5.5≦体長<6.4 : 1匹
② 以下の確率分布に従う確率変数を1つ取得する
P(1.5≦体長<2.4)=1/5
P(2.5≦体長<3.4)=1/5
P(3.5≦体長<4.4)=1/5
P(4.5≦体長<5.4)=1/5
P(5.5≦体長<6.4)=1/5
①と②を同じプロセスだとみなします。
①と②を同じだと見なすプロセスは、単純ランダムサンプリングで得たデータを基に、未知の母集団を推測する、ということです。
つまり、既知データから未知のデータを推測するという統計学のプロセスがここに詰まっているという私の理解です。
これまでのプロセスをすべてまとめると下記のように表現できます。
母集団分布に従う確率変数として、3cmの魚というデータが実現値として得られた
その他参考サイト
確率変数とは - 統計WEB
サンプリング方法の種類~データの取り方~ - Knowledge Makers
コメント
今回用いた魚を釣るという例は、箱の中にある球を取り出すという事象で表現することも可能ですね。
私は球を取り出すモデルは、中学・高校でも確率の問題でよく題材にされるので、イメージは行いやすい印象でした。