LoginSignup
23
30

More than 1 year has passed since last update.

@tanaka_benkyo

python+opencvで画像処理の勉強8 パターン・図形・特徴の検出とマッチング

Last updated at Posted at 2022-03-23

pythonとopencvを使って画像処理を勉強していきます。
今回もschikit-imageなども使用します。

説明が不十分であったりコードが見づらい部分もあると思いますがご了承ください。

前回
python+opencvで画像処理の勉強7 領域処理

テンプレートマッチングによるパターンの検出

テンプレートマッチング

2つの画像が同じかどうかを判断するために、画像を重ね合わせて違いを調べるような処理を一般にマッチングと呼びます。
画像の視覚的特徴や画素値そのものをパターンと呼び、パターンの存在や位置を検出することをパターンマッチングと呼びます。
あらかじめ標準パターンをテンプレートとして用意しておき、入力画像とのマッチングを行うことをテンプレートマッチングと呼びます。
テンプレート画像を画像全体に対して移動し、それぞれの位置で類似度を調べるとき、これを画像の左端から水平方向に、それを順次下の行に向かって探索することをラスタスキャンと呼びます。

類似度

テンプレートマッチングでは、2つの画像間の類似度または相違度を調べるために、SSDやSADを利用することが多いです。

    R_{SSD}=\sum_{j=0}^{N-1}\sum_{i=0}^{M-1}(I(i,j)-T(i,j))^2\\
    R_{SAD}=\sum_{j=0}^{N-1}\sum_{i=0}^{M-1}|I(i,j)-T(i,j)|

これらは、一致したときに0となるので、相違度を表しています。
類似度として、以下のNCCを利用することもあります。

    R_{NCC}=\frac{\sum_{j=0}^{N-1}\sum_{i=0}^{M-1}I(i,j)T(i,j)}
                 {\sqrt{\sum_{j=0}^{N-1}\sum_{i=0}^{M-1}I(i,j)^2×\sum_{j=0}^{N-1}\sum_{i=0}^{M-1}T(i,j)^2}}

テンプレートと対象画像のベクトルを$\boldsymbol{T}$と$\boldsymbol{I}$と考えると、
SADは先端間の市街地距離、SSDはユークリッド距離の2乗、NCCはベクトルのなす角を表しています。
また、以下の相互相関係数を類似度として利用することもあります。

    R_{ZNCC}=\frac{\sum_{j=0}^{N-1}\sum_{i=0}^{M-1}(I(i,j)-\bar{I})(T(i,j)-\bar{T})}
                  {\sqrt{\sum_{j=0}^{N-1}\sum_{i=0}^{M-1}(I(i,j)-\bar{I})^2×\sum_{j=0}^{N-1}\sum_{i=0}^{M-1}(T(i,j)-\bar{T})^2}}

ここで、$\bar{I}$と$\bar{T}$は領域内の画素値の平均値です。

    \bar{I}=\sum_{j=0}^{N-1}\sum_{i=0}^{M-1}I(i,j),\bar{T}=\sum_{j=0}^{N-1}\sum_{i=0}^{M-1}T(i,j)

サブピクセル位置推定

類似度や相違度の最大値または最小値を与える位置から、画素単位でテンプレートの位置が得られます。
さらに精密に求めるためにフィッティング関数で補間し、サブピクセルの位置を求める手法が**サブピクセル位置推定（類似度補間手法）**です。
相違度が最小の位置における相違度の値を$R(0)$、その隣接位置での値を$R(-1),R(1)$とします。
等角直線補正

    \hat{d}=
    \begin{cases}
        \frac{1}{2} \frac{R(1)-R(-1)}{R(0)-R(-1)} & (R(1)<R(-1)) \\
        \frac{1}{2} \frac{R(1)-R(-1)}{R(0)-R(1)} & (それ以外)
    \end{cases}

パラボラフィッティング

    \hat{d}=\frac{R(-1)-R(1)}{2R(-1)-4R(0)+2R(1)}

高速探索法

残差逐次検定法

SADを計算するとき、領域内の差の絶対値を加算しています。
加算の途中で残差があるしきい値を超えたら、検出位置ではないと判断し、加算を打ち切りつぎの位置での計算に移る方法が残差逐次検定法です。

疎密探索法

画像情報を何段階かの解像度で表現し、効率的に探索する方法を粗密探索法と呼びます。
イメージピラミッドを構成し、低解像度画像から順に探索を行います。

参照画像の選択による高速化

テンプレートに含まれるがそから同時生起行列を用いて選択された独自性の高い画素を用いて類似度計算することで、高速にマッチングを行います。
同時生起行列の確立を計算し、確率が小さいパターンほど独自性が高いと言えます。

cv2.matchTemplateでテンプレートマッチングを行います。
左がテンプレート画像、2番目の画像が計算結果の画像、一番右の画像が検出結果です。

import numpy as np
import matplotlib.pyplot as plt
import cv2

templ = img_rgb1[150:250,700:800]
test = img_rgb1.copy()

result = cv2.matchTemplate(test, templ, cv2.TM_CCOEFF_NORMED)
mmr = cv2.minMaxLoc(result)
pos = mmr[3]

dst = test.copy()
cv2.rectangle(dst, pos, (pos[0] + templ.shape[1], pos[1] + templ.shape[0]), (0, 255, 0), 2)

fig, ax = plt.subplots(1, 3, figsize=(15, 6), subplot_kw=({"xticks":(), "yticks":()}))
ax[0].imshow(templ);
ax[1].imshow(result);
ax[2].imshow(dst);

image.png

エッジ情報とヒストグラムによるパターン検出

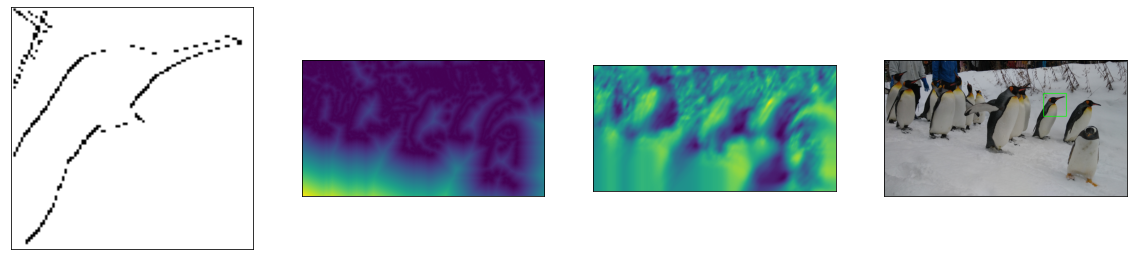
エッジ情報を用いたチャンファーマッチング

エッジ相違度を用いて行うテンプレートマッチングをチャンファーマッチングと呼びます。
まず、エッジ画像を作成し、距離変換処理を行い距離変換画像を作成します。
入力画像から作成した距離変換画像とテンプレート画像から作成したエッジ画像を、相違度に基づいてマッチングを行います。

# 2値化処理
ret, thresh = cv2.threshold(img_gray1, 100, 255, cv2.THRESH_BINARY)
test = thresh.copy()
test = cv2.bitwise_not(cv2.Sobel(test, -1, 1, 1, ksize=3))

# 距離画像
dist_test = cv2.distanceTransform(test,cv2.DIST_L2,3)

# テンプレート画像の作成
templ = thresh[150:250,700:800].copy()
templ = cv2.bitwise_not(cv2.Sobel(templ, -1, 1, 1, ksize=3)).astype('float32')

# テンプレートマッチング
# 距離画像に対して、エッジ画像のテンプレートでマッチング
result = cv2.matchTemplate(dist_test, templ, cv2.TM_CCOEFF_NORMED)
mmr = cv2.minMaxLoc(result)
pos = mmr[3]

dst = img_rgb1.copy()
cv2.rectangle(dst, pos, (pos[0] + templ.shape[1], pos[1] + templ.shape[0]), (0, 255, 0), 2)

fig, ax = plt.subplots(1, 4, figsize=(20, 6), subplot_kw=({"xticks":(), "yticks":()}))
ax[0].imshow(templ, 'gray')
ax[1].imshow(dist_test);
ax[2].imshow(result);
ax[3].imshow(dst);

image.png

ヒストグラム情報を用いたアクティブ探索

カラーヒストグラムの類似度

カラーヒストグラムは、カラー空間を量子化した際の各色番号に対する頻度を表したものです。
ヒストグラムインタセクション は、以下のようにカラーヒストグラムの各色番号における頻度の大小を比べ、小さいほうの頻度の和です。

    \rho(p,q)=\sum_{i=1}^{n}min(p_{i},q_{i})

バタチャリア係数では、各色番号における頻度を掛け合わせて、その総和を求めます。

    \rho(p,q)=\sum_{i=1}^{n}\sqrt{p_{i}q_{i}}

以下に例を示します。
ヒストグラムインタセクション（交差）、バタチャリア係数の他にカイ2乗と相関による類似度の計算結果も示します。

まず、ヒストグラムの計算とヒストグラムの類似度を計算する関数を定義します。

def calc_hists(img_rgb, n_bins, hist_range):
    img = img_rgb[:,:,0]*256**2+img_rgb[:,:,1]*256+img_rgb[:,:,2]
    img = img.reshape(img_rgb.shape[0],img_rgb.shape[1],1)
    
    hist = cv2.calcHist([img.astype('uint8')], channels=[0], mask=None, histSize=[n_bins], ranges=hist_range)
    hist = hist.squeeze(axis=-1)
    return hist

def calc_compare(hist1, hist2):
    hist_norm1 = hist1 / hist1.sum()
    hist_norm2 = hist2 / hist2.sum()
    
    print('相関: ',cv2.compareHist(hist1, hist2, method=cv2.HISTCMP_CORREL))
    print('カイ2乗: ',cv2.compareHist(hist_norm1, hist_norm2, method=cv2.HISTCMP_CHISQR))
    print('交差(ヒストグラムインタセクション): ',cv2.compareHist(hist_norm1, hist_norm2, method=cv2.HISTCMP_INTERSECT))
    print('Bhattacharyya距離: ',cv2.compareHist(hist_norm1, hist_norm2, method=cv2.HISTCMP_BHATTACHARYYA))

次の3つの画像で計算を行います。
ポスタリゼーション処理をしたものを使用します。


def make_post_lut(n):
    """
    ポスタリゼーション用のLUTを作成
    """
    x = np.arange(256)
    y = np.floor(x/n)*int(255/np.floor(255/n))
    y = y.astype('uint8')
    return y

y=make_post_lut(16)

for i in range(3):
    img_rgb1[:,:,i] = img_lut = cv2.LUT(img_rgb1[:,:,i], y)
    img_rgb2[:,:,i] = img_lut = cv2.LUT(img_rgb2[:,:,i], y)
    img_rgb3[:,:,i] = img_lut = cv2.LUT(img_rgb3[:,:,i], y)

fig, ax = plt.subplots(1, 3, figsize=(15, 6), subplot_kw=({"xticks":(), "yticks":()}))
ax[0].imshow(img_rgb1);
ax[1].imshow(img_rgb2);
ax[2].imshow(img_rgb3);

image.png

n_bins = 256**3  # ビンの数
hist_range = [0, 256**3]  # 集計範囲

hist1 = calc_hists(img_rgb1, n_bins, hist_range)
hist2 = calc_hists(img_rgb2, n_bins, hist_range)
hist3 = calc_hists(img_rgb3, n_bins, hist_range)

print('img1 vs img2')
calc_compare(hist1, hist2)
print('\nimg1 vs img3')
calc_compare(hist1, hist3)
print('\nimg2 vs img3')
calc_compare(hist2, hist3)

img1 vs img2
相関:  0.9834133201270742
カイ2乗:  0.07511080050000549
交差(ヒストグラムインタセクション):  0.8744612194714136
Bhattacharyya距離:  0.10087956066356284

img1 vs img3
相関:  0.1475005397660085
カイ2乗:  11070.45007625743
交差(ヒストグラムインタセクション):  0.21563268383818013
Bhattacharyya距離:  0.7129060431936752

img2 vs img3
相関:  0.11654969942055406
カイ2乗:  4.032504887971878
交差(ヒストグラムインタセクション):  0.18221196107333526
Bhattacharyya距離:  0.7376720171928234

特徴点検出

画像間の対応位置を求めるときに、画像中の特徴点をまず検出して、その特徴点の対応を探索することがあります。
コーナーや特徴点、輪郭線を検出する方法を説明します。

コーナー検出

ハリスのコーナー検出

画像からコーナーを検出する代表的な手法であるハリスのコーナー検出の手順を示します。

  1. 入力画像$I$に対し、ガウス関数$G(\sigma)$をx,yの各方向で微分した$G_{x}(\sigma),G_{y}(\sigma)$を畳み込み、勾配画像を求める。
    $I_{x}=G_{x}(\sigma)*I, \quad I_{y}=G_{y}(\sigma)*I$
  2. 各勾配画像の積により、各方向における勾配の大きさを算出する。
    $I_{xx}=I_{x}・I_{x},\quad I_{yy}=I_{y}・I_{y},\quad I_{xy}=I_{x}・I_{y}$
  3. $I_{xx},I_{yy},I_{xy}$の局所領域における勾配の総和$S_{xx},S_{yy},S_{xy}$を求める。
    以下に示すようなガウス関数$G(\sigma')$による重み付き和を用いることが多い。
    $S_{xx}=G(\sigma')*I_{xx},\quad S_{yy}=G(\sigma')*I_{yy},\quad S_{xy}=G(\sigma')*I_{xy}$
  4. 以下の行列$M(x,y)$を定義する。
    M(x,y)=
    \left[\begin{array}{cc}
    S_{xx}(x,y)&S_{xy}(x,y)\\
    S_{xy}(x,y)&S_{yy}(x,y)
    \end{array}\right]
  1. 画素(x,y)がコーナーである場合、行列$M(x,y)$の固有値$\lambda_{1},\lambda_{2}$はともに大きい値となる。
    そこで、コーナー関数$R$を以下のように定義する。$k$は調整パラメータである。
    R = detM - k (trM)^2\\
    detM = \lambda_{1}\lambda_{2},\quad trM = \lambda_{1}+\lambda_{2}
  1. Rの値が局所的な最大値となる画素をコーナーとして検出する。
    適当なしきい値を設け、有効なコーナーだけを選択する。

FASTによるコーナー検出

FAST(Feature from Accelerated Segment Test) のコーナー検出は、決定木をトラバーサルしてたどり着いた末端ノードが保持する情報により、コーナーを検出する方法であります。
まず、注目画素$p(x,y)$を中心とする周囲16画素を考えます。
周囲16画素の画素値が注目画素の画素値よりも明るい場合はBrighter、暗い場合はDarker、類似している場合はSimilarと3値化します。
BrighterまたはDarkerが一定数以上連続する場合に、注目画素をコーナーとします。
FASTでは決定木を用いた判定を行います。

Shi-Tomasiのコーナー検出

ハリスのコーナー検出を改善したもの。物体追跡に有用です。

gray = np.float32(img_gray)

# ハリスのコーナー検出
color1 = img_rgb.copy()
dst = cv2.cornerHarris(gray, 7, 11, 0.05)
dst = cv2.dilate(dst, None)
color1[dst>0.02*dst.max()]=[0,0,255]

# FASTによるコーナー検出
color2 = img_rgb.copy()
fast = cv2.FastFeatureDetector_create(threshold=25)
kp = fast.detect(img_gray, None)
color2 = cv2.drawKeypoints(color2, kp, None, color=(255,0,0))

# Shi-Tomasiのコーナー検出
color3 = img_rgb.copy()
corners = cv2.goodFeaturesToTrack(gray,200,0.05,10)
corners = np.int0(corners)
for i in corners:
    x,y = i.ravel()
    cv2.circle(color3,(x,y),3,255,-1)

fig, ax = plt.subplots(1, 3, figsize=(15, 4), subplot_kw=({"xticks":(), "yticks":()}))

ax[0].imshow(color1);
ax[0].set_title('Harris')
ax[1].imshow(color2);
ax[1].set_title('FAST')
ax[2].imshow(color3);
ax[2].set_title('Shi-Tomasi')

image.png

DoG画像を用いた特徴点とスケールの検出

画像中に拡大縮小があると、画像間の特徴点領域の濃淡パターンが変化するため、特徴点の対応付けができません。
特徴点とその領域の大きさを表すスケールを検出する必要があり、複数のDoG画像で計算することができます。
DoGはスケールの異なるガウス関数$G(\sigma)$と入力画像$I$を畳み込んだ平滑化画像$L$の差分により求めます。

    D(\sigma)=(G(k\sigma)-G(\sigma))*I=L(k\sigma)-L(\sigma)

$k$は$\sigma$の増加率であり、スケールを少しずつ大きくして複数のDoG画像を求めます。

ここでは、DoGフィルタによる特徴点の検出に加え、
LoGフィルタ、そしてDoHフィルタを用いた特徴点の検出の例を示します。
LoGフィルタは、ガウシアンフィルタで平滑化した画像に対し、ラプラシアンフィルタを適用するフィルタです。
DoHフィルtは、ヘッセ行列を用いた特徴点の検出法です。
scjikit-imageを使用します。

from skimage.feature import blob_dog, blob_log, blob_doh
from skimage.color import rgb2gray

color = img_rgb.copy()
gray = rgb2gray(img_rgb)

# DoG
blobs_dog = blob_dog(gray, max_sigma=30, threshold=.1)
blobs_dog[:, 2] = blobs_dog[:, 2] * np.sqrt(2)

# LoG
blobs_log = blob_log(gray, max_sigma=30, num_sigma=10, threshold=.1)
blobs_log[:, 2] = blobs_log[:, 2] * np.sqrt(2)

# DoH
blobs_doh = blob_doh(gray, max_sigma=30, threshold=.001)

fig, ax = plt.subplots(1, 3, figsize=(15, 4), subplot_kw=({"xticks":(), "yticks":()}))

titles = ['DoG','LoG','DoH']
for i, blobs in enumerate([blobs_dog, blobs_log, blobs_doh]):
    color = img_rgb.copy()
    for blob in blobs:
        x,y,r = blob
        cv2.circle(color,(int(x),int(y)),radius=int(r),color=255, thickness=2)
    ax[i].imshow(color)
    ax[i].set_title(titles[i])

image.png

特徴点の記述とマッチング

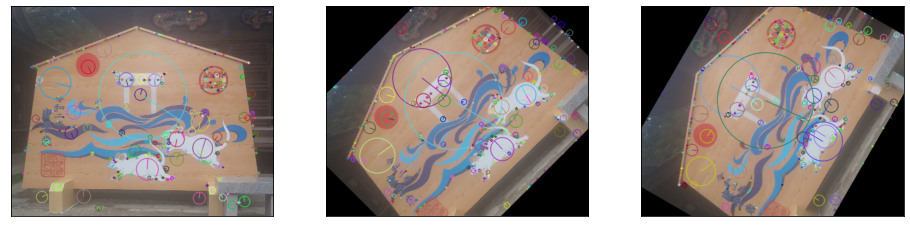
スケールと回転に不変な特徴記述(SIFT)

SIFTの特徴記述は、検出したスケールい合わせた領域に対して、回転に不変な特徴量を記述するためにオリエンテーションを算出します。
オリエンテーションは特徴点における方向を表します。
特徴点のスケールに合わせた局所領域内の平滑化画像$L(x,y)$から勾配強度$m(x,y)$と勾配方向$\theta(x,y)$を求めます。

    m(x,y)=\sqrt{f_{x}(x,y)^2+f_{y}(x,y)^2}\\
    \theta(x,y)=\tan^{-1}\frac{f_{y}(x,y)}{f_{x}(x,y)}\\
    f_{x}(x,y)=L(x+1,y)-L(x-1,y)\\
    f_{y}(x,y)=L(x,y+1)-L(x,y-1)

勾配強度と勾配方向から、重み付き勾配方向ヒストグラムを作成します。勾配方向は36方向に量子化し、中心に近いほど高く重み付けして投票します。
オリエンテーション方向に特徴記述する矩形領域を回転し、勾配情報に基づく特徴量を記述します。
オリエンテーション方向に座標軸を合わせた領域で特徴量を記述するため、回転に不変な特徴量です。

color = img_rgb.copy()
h, w = color.shape[:2]

fig, ax = plt.subplots(1, 3, figsize=(16, 4), subplot_kw=({"xticks":(), "yticks":()}))

for i, degree in enumerate([0.0,45.0,60.0]):
    affine_trans = cv2.getRotationMatrix2D((w//2,h//2), degree, 1.0)
    
    img = cv2.warpAffine(color, affine_trans, (w, h))
    
    detector = cv2.xfeatures2d.SIFT_create()
    kp = detector.detect(img, None)

    img=cv2.drawKeypoints(img,kp,gray,flags=cv2.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS)
    ax[i].imshow(img);

image.png

SURF

SURFは，SIFTの高速化版であり、SIFTはLoGをDoGを用いて近似していたところを、ボックスフィルタを使ってこの近似を行ったものです。

color = img_rgb.copy()
h, w = color.shape[:2]

fig, ax = plt.subplots(1, 3, figsize=(16, 4), subplot_kw=({"xticks":(), "yticks":()}))

for i, degree in enumerate([0.0,45.0,60.0]):
    affine_trans = cv2.getRotationMatrix2D((w//2,h//2), degree, 1.0)
    
    img = cv2.warpAffine(color, affine_trans, (w, h))
    
    detector = cv2.xfeatures2d.SURF_create()
    kp, des = detector.detect(img, None)

    img=cv2.drawKeypoints(img,kp,gray,flags=cv2.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS)
    ax[i].imshow(img);

使用するためには設定が必要です。ここでは行いません。

'\nsurf =cv2.xfeatures2d.SURF_create()\nkp, des = surf.detectAndCompute(img,None)\nimg2 = cv2.drawKeypoints(img_gray,kp,None,(255,0,0),4)\n\nplt.imshow(img2),plt.show()\n'

SURFは商用利用不可のアルゴリズムです（siftは商用利用可能となっています）

KAZE特徴量・AKAZE特徴量

非線形拡散フィルタを用いて算出する特徴量です。
AKAZEはKAZEを高速化したものとなります。

# KAZE特徴量
kaze =cv2.KAZE_create()
kp, des = kaze.detectAndCompute(img_rgb,None)
img1 = cv2.drawKeypoints(img_rgb,kp,None,(255,0,0),4)

# AKAZE特徴量
akaze =cv2.AKAZE_create()
kp, des = akaze.detectAndCompute(img_rgb,None)
img2 = cv2.drawKeypoints(img_rgb,kp,None,(255,0,0),4)

fig, ax = plt.subplots(1, 2, figsize=(10, 4), subplot_kw=({"xticks":(), "yticks":()}))
ax[0].imshow(img1);
ax[0].set_title('KAZE')
ax[1].imshow(img2);
ax[1].set_title('AKAZE')

image.png

2値特徴量

SIFT特徴量は計算に時間を要するというデメリットがあります。
そこで特徴量を2値ベクトルで表現する手法が提案されています。
BRIEFは、ランダムに選択された2点の画素値の差の符号かｒ2値特徴量を生成します。
ORBは、BRIEFの処理におけるサンプリングペアを教師なし学習で決定します。
BRISKは、BRIEFを発展させた方法で、スケール不変性と回転不変性を得ています。

method =[cv2.ORB_create(), cv2.BRISK_create()]
method_names = ['ORB', 'BRISK']

fig, ax = plt.subplots(1, 3, figsize=(16, 4), subplot_kw=({"xticks":(), "yticks":()}))

# ORB BRISK
for i in range(len(method)):
    color= img_rgb.copy()
    
    detector = method[i]
    kp = detector.detect(color, None)
    
    img=cv2.drawKeypoints(color, kp, color, flags=cv2.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS)
    ax[i].imshow(img);
    ax[i].set_title(method_names[i]);

# BRIEF
color= img_rgb.copy()
star = cv2.xfeatures2d.StarDetector_create()
brief = cv2.xfeatures2d.BriefDescriptorExtractor_create()
kp = star.detect(color,None)
kp, des = brief.compute(color, kp)
img=cv2.drawKeypoints(color, kp, color, flags=cv2.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS)

ax[2].imshow(img);
ax[2].set_title('BRIEF');

BRIEFは商用利用不可のアルゴリズムです

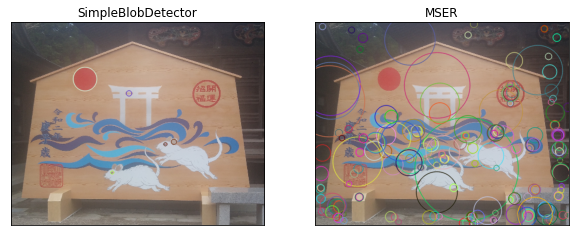
image.png

その他の特徴量

ブロブを検出する特徴量の例を示します。

method =[cv2.SimpleBlobDetector_create(), cv2.MSER_create()]
method_names = ['SimpleBlobDetector', 'MSER']

fig, ax = plt.subplots(1, 2, figsize=(10, 4), subplot_kw=({"xticks":(), "yticks":()}))
for i in range(len(method)):
    color = img_rgb.copy()
    
    detector = method[i]
    kp = detector.detect(color, None)
    
    img=cv2.drawKeypoints(color, kp, color, flags=cv2.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS)
    ax[i].imshow(img);
    ax[i].set_title(method_names[i]);

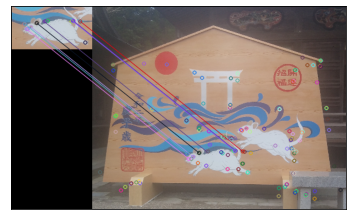
image.png

対応点マッチング

異なる画像間で検出された各特徴点の特徴量を比較することで、画像間の対応付けが可能となります。
画像$I_{1}$の特徴量を$x$、画像$I_{2}$の特徴量を$y$としたとき、2つの特徴量の類似度は、ユークリッド距離の2乗distにより算出できます。

    dist(x,y)=\sum_{i=1}^{128}(x_{i}-y_{i})^2

画像$I_{1}$のある1つの特徴点と画像$I_{2}$の全特徴点との距離を算出し、最も小さいもの、2番目に小さいものを
$dist_{1}(x,y)$、$dist_{2}(x,y)$とします。
比率テストを行い、信頼の高い特徴点と対応点を判定します。

    \frac{dist_{1}(x,y)}{dist_{2}(x,y)}\leq k

$k$を小さくすると対応点が減少します。

img = img_rgb.copy()
templ = img_rgb[240:320, 150:300]

# 2つの画像で特徴点の検出
detector = cv2.KAZE_create()
keypoints1, descriptor1 = detector.detectAndCompute(templ, None)
keypoints2, descriptor2 = detector.detectAndCompute(img, None)

# マッチング
matcher = cv2.BFMatcher()
matches = matcher.knnMatch(descriptor1, descriptor2, k=2)

# マッチング精度が高いもののみ抽出
ratio = 0.5
good = []
for m, n in matches:
    if m.distance < ratio * n.distance:
        good.append([m])

dst = cv2.drawMatchesKnn(templ, keypoints1, img, keypoints2, good, None, flags=0)
plt.imshow(dst, cmap="gray");
plt.xticks([]);
plt.yticks([]);

image.png

図形要素検出

ハフ変換

xy画像空間中の直線は、$\hat{a}$を傾き、$\hat{b}$を切片としたとき、以下のように表されます。

y=\hat{a}x+\hat{b}

abパラメータ空間では、xy画像空間中の直線を1点で表すことができます。
xy画像空間中の直線$l$上の点$(x_{i},y_{i})$は、以下によってabパラメータ空間に写像されます。

b=-x_{i}a+y_{i}

abパラメータ空間では、xy画像空間中の点を傾き$-x_{i}$、切片${y_{i}}$で表すことができます。
複数の点をabパラメータ空間に写像すると、点の数だけ直線が描画され、これらの直線は1点$(\hat{a},\hat{b})$で交差します。
このように直線検出原理をハフ変換と呼びます。
ハフ変換の処理は以下のように行われます。

  1. エッジ検出処理などで、出力画像を用意。2値化処理で、線の上に位置する可能性がある画素を用意する。
  2. abパラメータ空間を小さなセルに分割し、線候補画素をabパラメータ空間に写像したときに生成される直線が通過するセルの値を1増やす。
    この処理は投票と呼ばれる。
  3. この処理をすべての線候補画素について行う。結果、abパラメータ空間は直線の通過した回数を値として持つ（投票度数）。
  4. abパラメータ空間で。投票度数が大きなセルを探索すると、その座標がxy画像空間中の直線の傾きと切片に相当する。

また、xy画像空間中の直線を以下のように表し、パラメータ空間の大きさを制限することができます。

\hat{\rho}=x\cos{\hat{\theta}}+y\sin{\hat{\theta}}

ただし、$\hat{\rho}$は原点から直線までの符号付距離、\hat{\theta}は原点から直線への垂角です。
一方、xy画像空間中の直線$l$上の点$(x_{i},y_{i})$は、$\rho\theta$空間では正弦波に写像されます。

\rho=x_{i}\cos{\theta}+y_{i}\cos{\theta}=A\sin_{\theta+\alpha}

ただし、$A=\sqrt{x_{i}^2+y_{i}^2}$、$\alpha=\cos-{-1}(y_{i}/A)$です。

直線検出例

まずは、標準ハフ変換による検出例を示す。

img = img_rgb.copy()
edges = cv2.Canny(img_gray,200,150,apertureSize = 3)

lines = cv2.HoughLines(edges,1,np.pi/180,100)

for rho,theta in lines[:,0,:]:
    a = np.cos(theta)
    b = np.sin(theta)
    x0 = a*rho
    y0 = b*rho
    x1 = int(x0 + 1000*(-b))
    y1 = int(y0 + 1000*(a))
    x2 = int(x0 - 1000*(-b))
    y2 = int(y0 - 1000*(a))

    cv2.line(img,(x1,y1),(x2,y2),(0,0,255),2)

plt.imshow(img);
plt.xticks([]);
plt.yticks([]);

image.png

確率的ハフ変換による直線検出例を示す。

img = img_rgb.copy()
edges = cv2.Canny(img_gray,250,150,apertureSize = 3)

lines = cv2.HoughLinesP(edges,1,np.pi/180,50,minLineLength=80,maxLineGap=15)
for x1,y1,x2,y2 in lines[:,0,:]:
    cv2.line(img,(x1,y1),(x2,y2),(0,255,0),2)
    
plt.imshow(img);
plt.xticks([]);
plt.yticks([]);

image.png

円検出例

img = cv2.medianBlur(img_gray,19)
cimg = img_rgb.copy()

circles = cv2.HoughCircles(img,cv2.HOUGH_GRADIENT,1,60,
                            param1=30,param2=30,minRadius=0,maxRadius=100)

circles = np.uint16(np.around(circles))

for i in circles[0,:]:
    # draw the outer circle
    cv2.circle(cimg,(i[0],i[1]),i[2],(0,255,0),2)
    # draw the center of the circle
    cv2.circle(cimg,(i[0],i[1]),2,(0,0,255),3)
    
plt.imshow(cimg)
plt.xticks([]);
plt.yticks([]);

image.png

顕著性マップ

特徴統合理論

特徴統合理論とは、形状、色、明るさなどの情報に分解し、
注目した領域に対して組み合わせることで物体を認識するというものです。

顕著性マップ

顕著性マップとは、特徴統合理論に基づき、各特徴マップ生成時にそれぞれの特徴マップが独立に注意を引き付ける性質を持っていると考え、この性質を数値化したものです。
イッチらの計算モデルでは、画素値、色空間、勾配方向の3つの特徴マップを生成し、それぞれのマップから注目度を計算します。
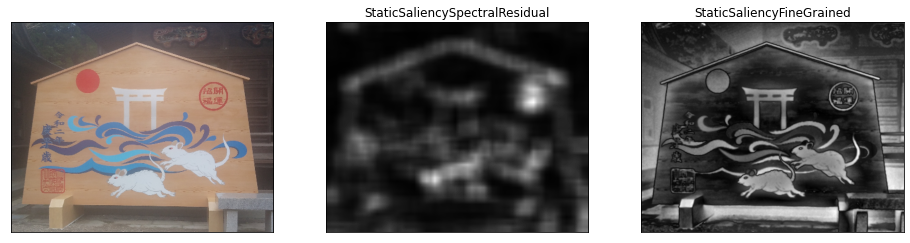
顕著性マップを利用することで画像中の重要な物体を捉えることができるため、シームカービングや人の注視点推定などに用いられます。

img = img_rgb.copy()
method = [cv2.saliency.StaticSaliencySpectralResidual_create(),
          cv2.saliency.StaticSaliencyFineGrained_create()]

method_name = ['StaticSaliencySpectralResidual',
               'StaticSaliencyFineGrained']

fig, ax = plt.subplots(1, 3, figsize=(16, 6), subplot_kw=({"xticks":(), "yticks":()}))
ax[0].imshow(img_rgb)

for i in range(2):
    saliency = method[i]

    (success, saliencyMap) = saliency.computeSaliency(img)
    saliencyMap = (saliencyMap * 255).astype("uint8")

    ax[i+1].imshow(saliencyMap, 'gray')
    ax[i+1].set_title(method_name[i])

image.png

次回

パターン認識

参考

ディジタル画像処理[改訂第二版] | ディジタル画像処理編集委員会 |本 | 通販 | Amazon

23
30
3

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
23
30