とても有名な「統計学入門」をpythonで実装しながら読んでいきます。
本をしっかり読むことと実装の勉強が目的ですので説明が不足していたりします。
また、実装方法に関してはベストなものではないと思いますのでご了承ください。
1次元のデータ
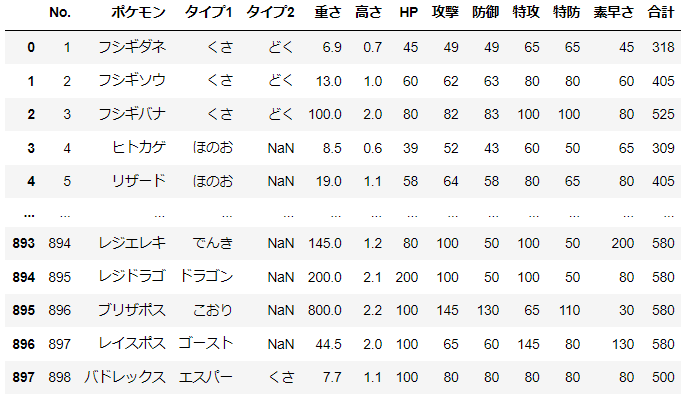
サンプルデータとして次のようなものを使用したいと思います。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
d = pd.read_csv('pokemon_for_stats.csv').iloc[:,1:]
d
度数分布とヒストグラム
度数分布表は、観測値の取り得る値をいくつかの階級に分け、それぞれの階級で観測値がいくつあるか度数を数えて表にしたものである。
階級値とは階級の代表する値のことであって、各階級の中で観測値は一様に分布していると仮定して、階級の上限値と下限値の中間値を階級値とするのが普通である。
相対度数は観測値の総数、すなわちデータ全体の大きさを1としたときの、各階級に属する観測値の個数の全体中での割合を示す。
累積度数、累積相対度数とは、度数を下の階級から順に積み上げたときの度数、相対度数の累積和である。
度数分布表からは、一般にヒストグラムまたは柱状グラフと呼ばれるグラフが描かれる。
それぞれの階級に対して階級幅を横幅とし柱の面積が度数と比例するように高さを定める。
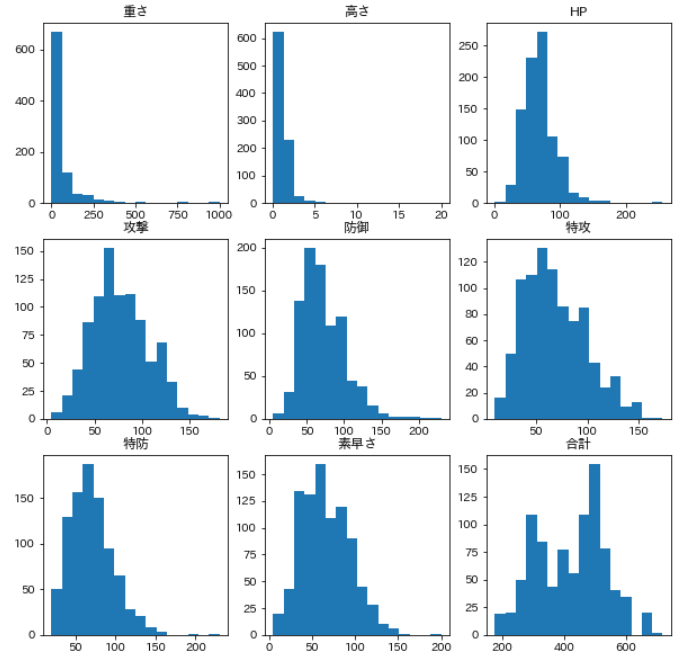
まず、各特徴量のヒストグラムを確認する。
num_cols = ['重さ','高さ','HP','攻撃','防御','特攻','特防','素早さ','合計']
fig, axes = plt.subplots(3, 3, figsize=(10,10))
for i, c in enumerate(num_cols):
axes[i//3][i%3].hist(d[c], bins=16);
axes[i//3][i%3].set_title(c)
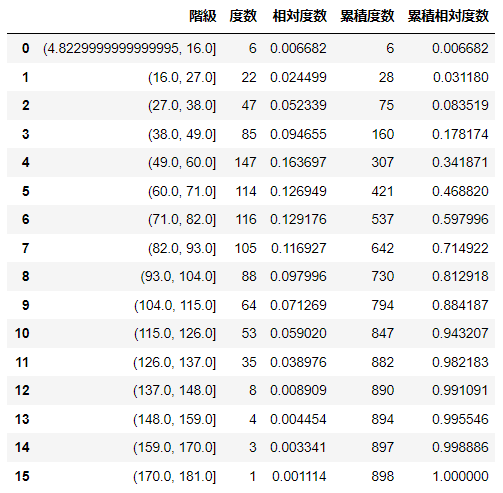
次に、「攻撃」について度数の計算を行い、相対度数と共に図に示す。
freq = d['攻撃'].value_counts(bins=16,sort=False)
hist_range = freq.index
hist_count = freq.values
df = pd.DataFrame({'階級':hist_range, '度数':hist_count.astype(int)})
df['相対度数'] = df['度数'] / sum(df['度数'])
df['累積度数'] = df['度数'].cumsum()
df['累積相対度数'] = df['相対度数'].cumsum()
df
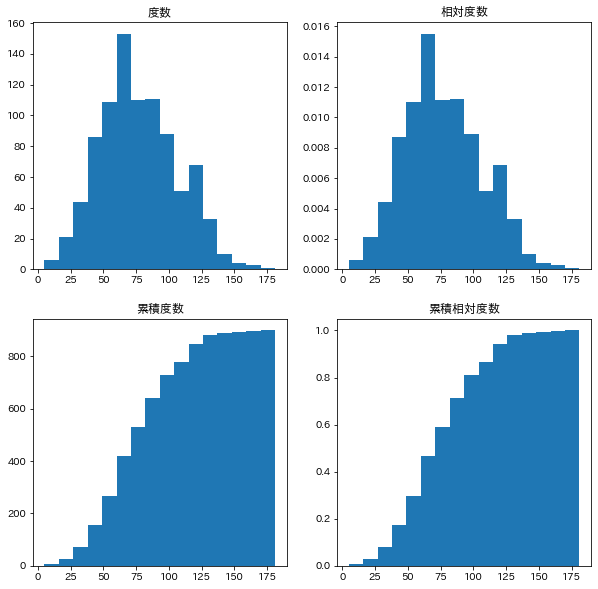
fig, axes = plt.subplots(2, 2, figsize=(10,10))
axes[0][0].hist(d['攻撃'], bins=16);
axes[0][0].set_title('度数');
axes[0][1].hist(d['攻撃'], bins=16, density=True);
axes[0][1].set_title('相対度数');
axes[1][0].hist(d['攻撃'], bins=16, cumulative=True);
axes[1][0].set_title('累積度数');
axes[1][1].hist(d['攻撃'], bins=16, cumulative=True, density=True);
axes[1][1].set_title('累積相対度数');
「攻撃」の分布は中央に一つの峰がある山型分布である。しかし、左右対称の山型分布にならないものも多くある。
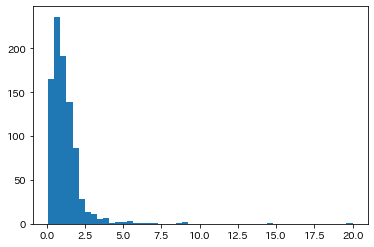
例えば、下の図の「高さ」の分布のように右側に長く裾を引く分布のことを右に歪んだ分布という。
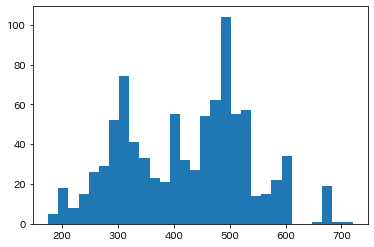
「合計」の分布のようにデータによっては峰が二つ以上ある分布(双方型)も生じることがある。
そのような場合、性質の異なるデータがまじりあっていることが多く、適当にグループ分けすると峰が一つの単純な分布(単峰型)が現れることが多い。このような操作を層別という。
plt.hist(d['高さ'], bins=50);
plt.hist(d['合計'], bins=30);
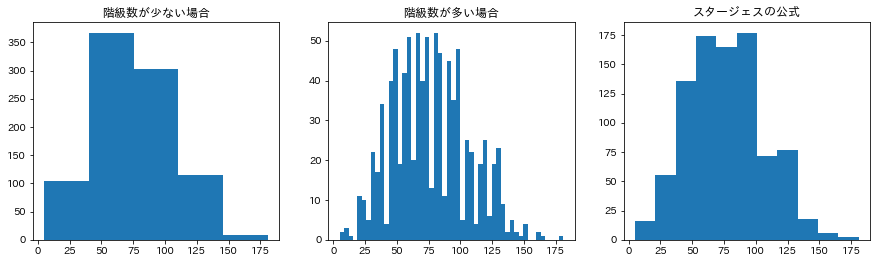
階級数については、階級数が少ないと荒すぎるためありふれた形となり真の分布を見出しえない。
一方、階級数が多すぎると階級によって小さなデコボコが生じて、真の分布が偶然性によって乱される場合が多い。
階級数の統一的なルールはないが、スタージェスの公式が参考になる。
$$
k\fallingdotseq 1+\log_2n=1+(\log_{10}n)/(\log_{10}2)
$$
fig, axes = plt.subplots(1, 3, figsize=(15,4))
axes[0].hist(d['攻撃'], bins=5);
axes[0].set_title('階級数が少ない場合')
axes[1].hist(d['攻撃'], bins=50);
axes[1].set_title('階級数が多い場合')
axes[2].hist(d['攻撃'], bins=int(np.ceil(1+np.log2(len(d)))));
axes[2].set_title('スタージェスの公式');
累積度数を組み合わせて書いた折れ線をローレンツ曲線と呼ぶ。ローレンツ曲線は分配の不平等さを示すのに用いられる。
対角線からの分離の度合が大きいほど、不平等に分布している。
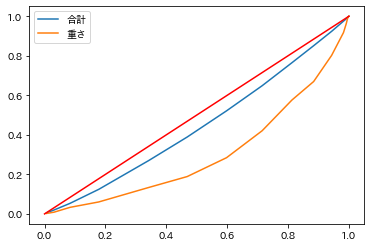
少し無理があるが、「攻撃」の累積相対度数と「合計」および「重さ」の累積相対度数を組み合わせたローレンツ曲線を示す。
「攻撃」と「合計」については平等に振り分けられているが、「攻撃」と「重さ」については直線からの分離が大きい。
「重さ」が大きいポケモンに大きな「攻撃」をもったものが含まれている可能性がある。
d['攻撃_bin'] = pd.cut(d['攻撃'], bins=hist_range)
d_agg = d.groupby(['攻撃_bin']).agg({'ポケモン':'count', '合計':'sum', '重さ':'sum'}).reset_index()
d_agg['ポケモン'] = d_agg['ポケモン'].cumsum() / d_agg['ポケモン'].sum()
d_agg['合計'] = d_agg['合計'].cumsum() / d_agg['合計'].sum()
d_agg['重さ'] = d_agg['重さ'].cumsum() / d_agg['重さ'].sum()
plt.plot(d_agg.ポケモン, d_agg.合計, label='合計')
plt.plot(d_agg.ポケモン, d_agg.重さ, label='重さ')
plt.plot([0,1], [0,1], 'red')
plt.legend();
代表値
代表値とは、分布を代表する値のことである。
最もよく知られている代表値は平均であり、その中でも特に算術平均と呼ばれる値である。
算術平均は観測値$x_1,x_2,\cdots,x_n$の和を観測値の総数、すなわちデータの大きさ$n$で割ったものであり、
$$
\bar{x}=\frac{x_1+\cdots+x_n}{n}
$$
と定義される。
離散型データの場合、各観測値に対してその値をとる度数を掛けて、その合計をデータの大きさで割ればよい。
観測値の取り得る値を$v_1,\cdots,v_k$とし、それぞれの度数が$f_1,\cdots,f_k$であるとすると、平均は
$$
\bar{x}=\frac{f_1v_1+\cdots+f_kv_k}{f_1+\cdots+f_k}
$$
によって求めることができる。
度数分布表から計算された平均値は階級値が使用されるため真の平均値とは一致しないことに注意する。
平均には、幾何平均$x_G$
$$
x_G=\sqrt[n]{x_1・x_2・\cdots・x_n}
$$
調和平均$x_H$
$$
\frac{1}{x_H}=\frac{1}{n}\biggl(\frac{1}{x_1}+\cdots+\frac{1}{x_n} \biggr)
$$
などがある。
d[num_cols].mean()
重さ 63.970045
高さ 1.185969
HP 69.031180
攻撃 76.544543
防御 71.897550
特攻 69.681514
特防 69.887528
素早さ 65.949889
合計 422.992205
メディアン(中位数、中央値)は、観測値を小さいものから順番に並び替えたときの中央の値である。
データ$x_1,\cdots,x_n$を大きさの順序に並び替えたものを、小さいものから$x_{(1)},\cdots,x_{(n)}$とかく。
メディアンは、データの大きさが奇数$n=2m+1$のときには$m+1$番目の観測値$x_{m+1}$であるが、
偶数$n=2m$の場合は、$m$番目と$m+1$番目の観測値$x_{m}$と$x_{m+1}$の平均$(x_{m}+x_{m+1})/2$をメディアンとする。
d[num_cols].median()
重さ 27.0
高さ 1.0
HP 65.0
攻撃 75.0
防御 67.0
特攻 65.0
特防 65.0
素早さ 65.0
合計 440.0
メディアンを拡張したものに分位点がある。
観測値を小さいものの順に並び替えたとき、小さい方から$100p$%($0\leq p \leq 1$)の所にある値を100pパーセンタイル((百)分位点)という。
よく用いられる分位点には四分位点がある。これはデータを4分割したときの3つの分割点であり、第1四分位点$Q_1$は25%分位点、第2四分位点$Q_2$は50%分位点(メディアン)、第3四分位点$Q_3$は75%分位点である。
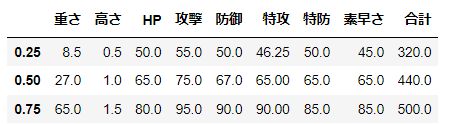
d[num_cols].quantile(q=[0.25,0.5,0.75])
np.quantile(d[num_cols], q=[0.25,0.5,0.75], axis=0)
array([[ 8.5 , 0.5 , 50. , 55. , 50. , 46.25, 50. , 45. , 320. ],
[ 27. , 1. , 65. , 75. , 67. , 65. , 65. , 65. , 440. ],
[ 65. , 1.5 , 80. , 95. , 90. , 90. , 85. , 85. , 500. ]])
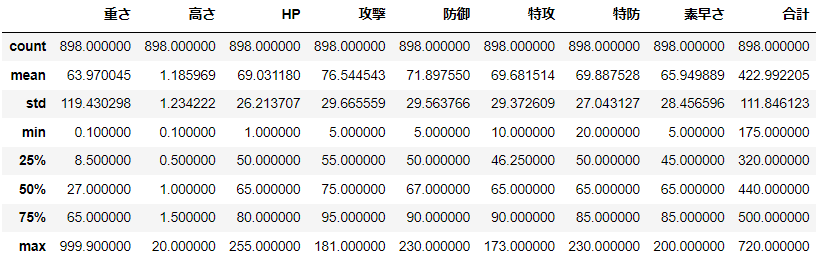
d[num_cols].describe()
モード(最頻値)とは、分布の峰に対応する値のことである。度数分布表においては、その頻度が最大である階級の階級値がモードとなる。
階級の取り方によって異なることや、峰が2つ以上ある場合には有効な代表値とはならないことに注意する。
num_cols = ['重さ','高さ','HP','攻撃','防御','特攻','特防','素早さ','合計']
fig, axes = plt.subplots(3, 3, figsize=(15,10))
for i, c in enumerate(num_cols):
mean = d[c].mean()
med = d[c].median()
a,b,_=axes[i//3][i%3].hist(d[c], bins=9, density=True);
max_count = np.max(a)*1.2
mode = (b[np.argmax(a)]+b[np.argmax(a)+1])/2
axes[i//3][i%3].plot([mean,mean], [0, max_count], label='mean');
axes[i//3][i%3].plot([med,med], [0, max_count], label='median');
axes[i//3][i%3].plot([mode,mode], [0, max_count], label='mode');
axes[i//3][i%3].set_title(c)
axes[i//3][i%3].legend()
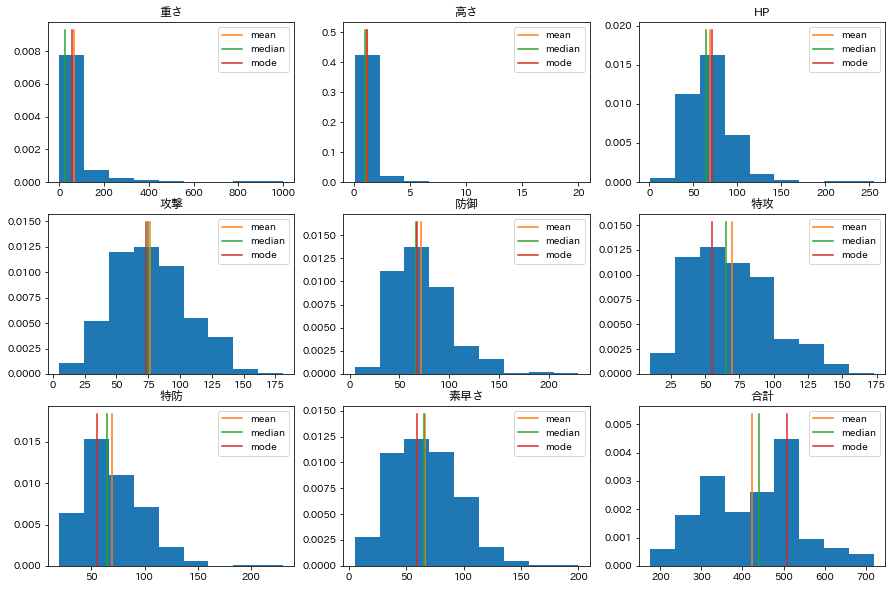
平均、メディアン、モードの3つの関係を確認する。
「攻撃」のように左右対称の場合この三つの値は完全に一致する。
「特攻」や「特防」のように峰が左側によっている場合、一般的に
$$
Mean>Median>Mode
$$
である(辞書に登場する順番と覚えればよい)。
散らばりの尺度
分布の形状を示す指標でよく用いられるものは散らばりの尺度と呼ばれるものである。
もっとも単純な散らばりの指標はレンジ(範囲)と呼ばれるものであって、
$$
R=\max (x_1,\cdots, x_n) - \min (x_1, \cdots, x_n)
$$
d[num_cols].max() - d[num_cols].min()
重さ 999.8
高さ 19.9
HP 254.0
攻撃 176.0
防御 225.0
特攻 163.0
特防 210.0
素早さ 195.0
合計 545.0
重さが広く分布しており、「特防」や「防御」は同じような値をとっている。
レンジは尺度としてかなり荒いものであり、「特防」や「防御」の分布の違いを記述することはできない。
レンジを改良したものとして次の式で定義される四分位偏差がある。
$$
Q=\frac{1}{2}(Q_3-Q_1)
$$
dq = d[num_cols].quantile(q=[0.25,0.75]).T
dq[0.75]-dq[0.25]
重さ 56.50
高さ 1.00
HP 30.00
攻撃 40.00
防御 40.00
特攻 43.75
特防 35.00
素早さ 40.00
合計 180.00
各観測値が平均からどれだけ離れているかについての平均を求めたものが平均偏差である。
$$
d=\frac{1}{n}\biggl\{|x_1-\bar{x}|+|x_2-\bar{x}|+\cdots+|x_n-\bar{x}| \biggr\}
$$
平均からの偏差は正負両符号を含むため絶対値を取っている。
np.abs(d[num_cols] - d[num_cols].mean()).mean(axis=0)
重さ 64.712695
高さ 0.664894
HP 19.124786
攻撃 24.234304
防御 22.876494
特攻 24.013943
特防 21.319795
素早さ 23.148209
合計 95.048318
絶対値ではなく2乗することで符号を消し、同様に平均を求めたものをデータの分散という。
$$
S^2=\frac{1}{n}\biggl\{(x_1-\bar{x})^2+(x_2-\bar{x})^2+\cdots+(x_n-\bar{x})^2 \biggr\}
$$
分散は単位が変わるので、単位を揃えるときには分散の平方根をとった$S$が用いられる。これを標準偏差と呼ぶ。
$$
S=\sqrt{S^2}
$$
まず分散を計算する。
((d[num_cols] - d[num_cols].mean())**2).mean(axis=0)
重さ 14247.712299
高さ 1.521607
HP 686.393237
攻撃 879.065388
防御 873.042956
特攻 861.789436
特防 730.516303
素早さ 808.876108
合計 12495.624661
d[num_cols].var(ddof=0)
重さ 14247.712299
高さ 1.521607
HP 686.393237
攻撃 879.065388
防御 873.042956
特攻 861.789436
特防 730.516303
素早さ 808.876108
合計 12495.624661
標準偏差の計算を行う。
np.sqrt(((d[num_cols] - d[num_cols].mean())**2).mean(axis=0))
重さ 119.363781
高さ 1.233534
HP 26.199108
攻撃 29.649037
防御 29.547300
特攻 29.356250
特防 27.028065
素早さ 28.440747
合計 111.783830
d[num_cols].std(ddof=0)
重さ 119.363781
高さ 1.233534
HP 26.199108
攻撃 29.649037
防御 29.547300
特攻 29.356250
特防 27.028065
素早さ 28.440747
合計 111.783830
分布の中心の位置が著しく異なる場合には分散をもって分布の散らばり具合を比較することはできない。
変動係数と呼ばれる、平均$\bar{x}$を考慮した上で散らばり具合を相対的に比較するのに便利な指標がある。
$$
C.V.=S_x/\bar{x}
$$
d[num_cols].mean() / d[num_cols].std(ddof=0)
重さ 0.535925
高さ 0.961440
HP 2.634868
攻撃 2.581687
防御 2.433304
特攻 2.373652
特防 2.585739
素早さ 2.318852
合計 3.784020
データを次のように変換した場合、
すなわち、平均を差し引き標準偏差で割って、位置。尺度の調整をした結果、
$$
z_i=\frac{x_i-\bar{x}}{S_x}
$$
平均は0、標準偏差は1にそろったことになる。
$z$を$x$の標準化や、標準得点と呼ぶ。
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
d_scaled = scaler.fit_transform(d[num_cols])
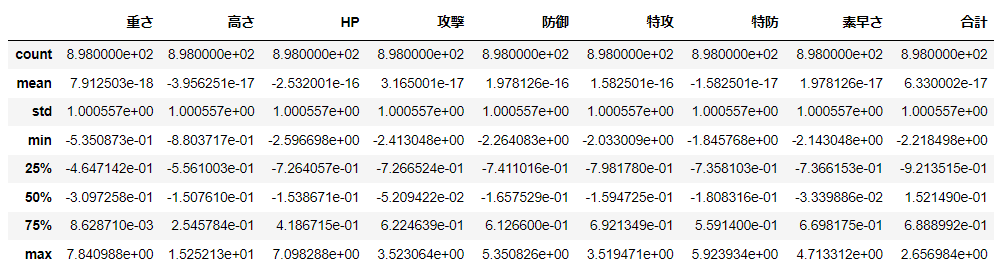
pd.DataFrame(d_scaled, columns=num_cols).describe()
次回
2次元のデータ
参考書