1. 勾配消失問題
1.1 要約
誤差逆伝搬法が下位層に進んでいくに連れて、勾配が緩やかになっていく。
そのため、勾配降下法による更新では下位層のパラメータはほとんど変わらず、
最適値に収束しなくなる。
解決方法として
- 活性化関数の選択
- 重みの初期値設定
- バッチ正規化
活性化関数の選択
ReLU関数は、勾配喪失問題の回避に貢献することで良い結果をもたらしている。
重みの初期値設定
- Xavier
ReLU関数、シグモイド関数、双曲線正接関数
重みの要素を、前の層のノード数の平方根で除算した値 - He
ReLU関数
重みの要素を、前の層のノード数の平方根で除算した値に対し、$\sqrt{2}$を掛け合わせた値
バッチ正規化
ミニバッチ単位で入力値のデータの偏りを抑制する手法
\mu_{\beta}=\frac{1}{m}\sum_{i=1}^mx_i\\
\sigma^2_{B}=\frac{1}{m}\sum_{i=1}^m(x_i-\mu_{\beta})^2\\
\hat{x}_i=\frac{x_i-\mu_{\beta}}{\sqrt{\sigma^2_{B}+\epsilon}}
さらに、固有のスケールとシフトで変換を行う。
y_i=\gamma\hat{x}_i+\beta
1.2 実装
出力の値の変化を確認する。
入力を(1000, 100)の乱数とし、100ノードの5層の中間層に入力して各層の出力の分布を見る。
ガウス分布(分散: 1)
activations = calc_a(1)
plt.figure(figsize=(20, 3))
for i, a in activations.items():
plt.subplot(1, len(activations), i+1)
plt.title(str(i+1) + "-layer")
plt.hist(a.flatten(), 30, range=(0,1))
plt.show()
0と1に偏った分布になっていることがわかる。
シグモイド関数の値が0または1に近づくにつれて、微分の値は0に近づく。
ガウス分布(分散: 0.01)
activations = calc_a(0.01)
plt.figure(figsize=(20, 3))
for i, a in activations.items():
plt.subplot(1, len(activations), i+1)
plt.title(str(i+1) + "-layer")
plt.hist(a.flatten(), 30, range=(0,1))
plt.show()
ガウス分布の場合、分散が小さいほうが勾配消失問題は起きにくいが、表現力に問題が出てくる。
ガウス分布(分散: 0.01)
node_num = 100
activations = calc_a(np.sqrt(1/node_num))
plt.figure(figsize=(20, 3))
for i, a in activations.items():
plt.subplot(1, len(activations), i+1)
plt.title(str(i+1) + "-layer")
plt.hist(a.flatten(), 30, range=(0,1))
plt.show()
Xavierの初期値
activations = calc_a(np.sqrt(2/node_num))
plt.figure(figsize=(20, 3))
for i, a in activations.items():
plt.subplot(1, len(activations), i+1)
plt.title(str(i+1) + "-layer")
plt.hist(a.flatten(), 30, range=(0,1))
plt.show()
import numpy as np
from common import layers
from collections import OrderedDict
from common import functions
from data.mnist import load_mnist
import matplotlib.pyplot as plt
class MultiLayerNet:
'''
input_size: 入力層のノード数
hidden_size_list: 隠れ層のノード数のリスト
output_size: 出力層のノード数
activation: 活性化関数
weight_init_std: 重みの初期化方法
'''
def __init__(self, input_size, hidden_size_list, output_size, activation='relu', weight_init_std='relu'):
self.input_size = input_size
self.output_size = output_size
self.hidden_size_list = hidden_size_list
self.hidden_layer_num = len(hidden_size_list)
self.params = {}
# 重みの初期化
self.__init_weight(weight_init_std)
# レイヤの生成, sigmoidとreluのみ扱う
activation_layer = {'sigmoid': layers.Sigmoid, 'relu': layers.Relu}
self.layers = OrderedDict() # 追加した順番に格納
for idx in range(1, self.hidden_layer_num+1):
self.layers['Affine' + str(idx)] = layers.Affine(self.params['W' + str(idx)], self.params['b' + str(idx)])
self.layers['Activation_function' + str(idx)] = activation_layer[activation]()
idx = self.hidden_layer_num + 1
self.layers['Affine' + str(idx)] = layers.Affine(self.params['W' + str(idx)], self.params['b' + str(idx)])
self.last_layer = layers.SoftmaxWithLoss()
def __init_weight(self, weight_init_std):
all_size_list = [self.input_size] + self.hidden_size_list + [self.output_size]
for idx in range(1, len(all_size_list)):
scale = weight_init_std
if str(weight_init_std).lower() in ('relu', 'he'):
scale = np.sqrt(2.0 / all_size_list[idx - 1])
elif str(weight_init_std).lower() in ('sigmoid', 'xavier'):
scale = np.sqrt(1.0 / all_size_list[idx - 1])
self.params['W' + str(idx)] = scale * np.random.randn(all_size_list[idx-1], all_size_list[idx])
self.params['b' + str(idx)] = np.zeros(all_size_list[idx])
def predict(self, x):
for layer in self.layers.values():
x = layer.forward(x)
return x
def loss(self, x, d):
y = self.predict(x)
weight_decay = 0
for idx in range(1, self.hidden_layer_num + 2):
W = self.params['W' + str(idx)]
return self.last_layer.forward(y, d) + weight_decay
def accuracy(self, x, d):
y = self.predict(x)
y = np.argmax(y, axis=1)
if d.ndim != 1 : d = np.argmax(d, axis=1)
accuracy = np.sum(y == d) / float(x.shape[0])
return accuracy
def gradient(self, x, d):
# forward
self.loss(x, d)
# backward
dout = 1
dout = self.last_layer.backward(dout)
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
# 設定
grad = {}
for idx in range(1, self.hidden_layer_num+2):
grad['W' + str(idx)] = self.layers['Affine' + str(idx)].dW
grad['b' + str(idx)] = self.layers['Affine' + str(idx)].db
return grad
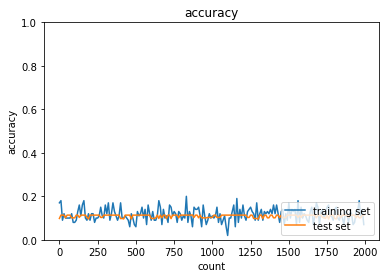
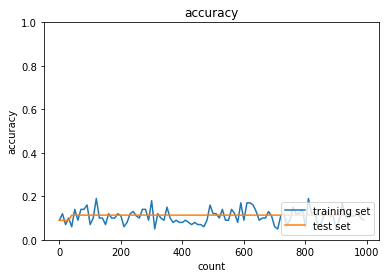
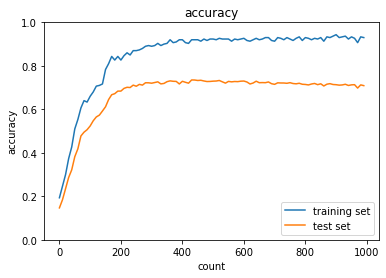
活性化関数:sigmoid関数・初期値:ガウス分布
# データの読み込み
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)
print("データ読み込み完了")
network = MultiLayerNet(input_size=784, hidden_size_list=[40, 20], output_size=10, activation='sigmoid', weight_init_std=0.01)
iters_num = 2000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1
train_loss_list = []
accuracies_train = []
accuracies_test = []
plot_interval=10
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
d_batch = d_train[batch_mask]
# 勾配
grad = network.gradient(x_batch, d_batch)
for key in ('W1', 'W2', 'W3', 'b1', 'b2', 'b3'):
network.params[key] -= learning_rate * grad[key]
loss = network.loss(x_batch, d_batch)
train_loss_list.append(loss)
if (i + 1) % plot_interval == 0:
accr_test = network.accuracy(x_test, d_test)
accuracies_test.append(accr_test)
accr_train = network.accuracy(x_batch, d_batch)
accuracies_train.append(accr_train)
if (i + 1) % 200 == 0:
print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
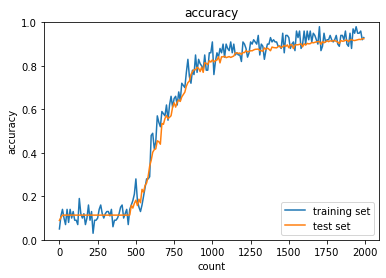
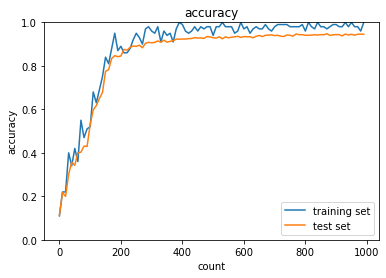
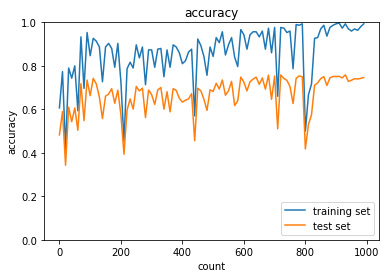
活性化関数:ReLU関数・初期値:ガウス分布
# データの読み込み
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)
print("データ読み込み完了")
network = MultiLayerNet(input_size=784, hidden_size_list=[40, 20], output_size=10, activation='relu', weight_init_std=0.01)
iters_num = 2000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1
train_loss_list = []
accuracies_train = []
accuracies_test = []
plot_interval=10
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
d_batch = d_train[batch_mask]
# 勾配
grad = network.gradient(x_batch, d_batch)
for key in ('W1', 'W2', 'W3', 'b1', 'b2', 'b3'):
network.params[key] -= learning_rate * grad[key]
loss = network.loss(x_batch, d_batch)
train_loss_list.append(loss)
if (i + 1) % plot_interval == 0:
accr_test = network.accuracy(x_test, d_test)
accuracies_test.append(accr_test)
accr_train = network.accuracy(x_batch, d_batch)
accuracies_train.append(accr_train)
if (i + 1) % 200 == 0:
print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
sigmoid関数は精度がほぼ変わらず勾配消失問題が起きていることが確認できるが、ReLUでは500エポックあたりから精度が上がり勾配消失問題に対処できていることがわかる。
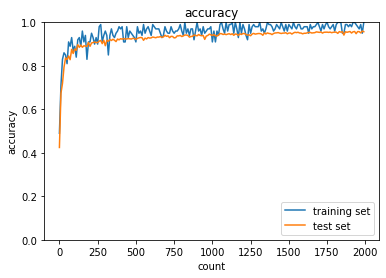
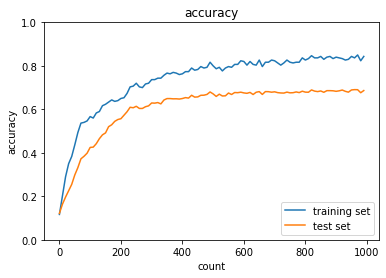
活性化関数:Sigmoid関数・初期値:Xavier
# データの読み込み
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)
print("データ読み込み完了")
network = MultiLayerNet(input_size=784, hidden_size_list=[40, 20], output_size=10, activation='sigmoid', weight_init_std='Xavier')
iters_num = 2000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1
train_loss_list = []
accuracies_train = []
accuracies_test = []
plot_interval=10
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
d_batch = d_train[batch_mask]
# 勾配
grad = network.gradient(x_batch, d_batch)
for key in ('W1', 'W2', 'W3', 'b1', 'b2', 'b3'):
network.params[key] -= learning_rate * grad[key]
loss = network.loss(x_batch, d_batch)
train_loss_list.append(loss)
if (i + 1) % plot_interval == 0:
accr_test = network.accuracy(x_test, d_test)
accuracies_test.append(accr_test)
accr_train = network.accuracy(x_batch, d_batch)
accuracies_train.append(accr_train)
if (i + 1) % 200 == 0:
print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
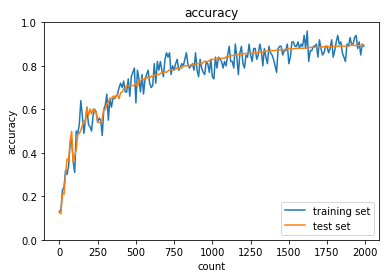
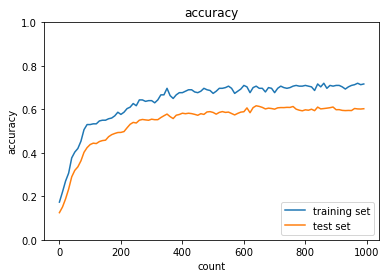
活性化関数:ReLU関数・初期値:He
# データの読み込み
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)
print("データ読み込み完了")
network = MultiLayerNet(input_size=784, hidden_size_list=[40, 20], output_size=10, activation='relu', weight_init_std='He')
iters_num = 2000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1
train_loss_list = []
accuracies_train = []
accuracies_test = []
plot_interval=10
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
d_batch = d_train[batch_mask]
# 勾配
grad = network.gradient(x_batch, d_batch)
for key in ('W1', 'W2', 'W3', 'b1', 'b2', 'b3'):
network.params[key] -= learning_rate * grad[key]
loss = network.loss(x_batch, d_batch)
train_loss_list.append(loss)
if (i + 1) % plot_interval == 0:
accr_test = network.accuracy(x_test, d_test)
accuracies_test.append(accr_test)
accr_train = network.accuracy(x_batch, d_batch)
accuracies_train.append(accr_train)
if (i + 1) % 200 == 0:
print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
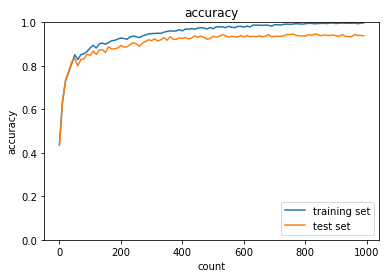
HeやXavierを使用した場合、ガウス分布の場合に比べて精度の向上が早くより効率的に学習できていることが分かる。
1.3 確認テスト
重みの初期値を0にした場合、どのような問題が発生するか。
値が一定のため表現力がさがり、精度があがらない。
一般的に考えられるバッチ正規化の効果を2点
- 学習を速く進行させることができる。
- 過学習を抑制する。
1.4 補足
活性化関数:Sigmoid関数・初期値:He
活性化関数:ReLU関数・初期値:Xavier
いずれも初期値の種類によらずガウス分布と比較して制度の向上の早さが確認できた。
2. 学習率最適化手法
2.1 要約
勾配降下法で最適なパラメータを探していくが、学習率によって更新のされ方が異なる。
学習率が大きい場合
- 最適値にたどりつかず発散
学習率が小さい場合
- 発散することはないが、収束までに時間がかかる
- 大域手局所解に収束しづらくなる
学習率最適化手法
- Momentum
- AdaGrad
- RMSProp
- Adam
Momentum
誤差をパラメータで微分したものと学習率の積を減算した後、
現在の重みに前回の重みを減算した値と慣性の積を加算する。
V_t = \mu V_{t-1}-\epsilon \nabla E\\
\boldsymbol{w}^{(t+1)}=\boldsymbol{w}^{(t)}+V_t
ここで$\mu$は慣性である。
局所的最適解にはならず、大域的最適解となり、谷間についてから最も低い位置に到達するまでの時間が早い。
AdaGrad
誤差をパラメータで微分したものと再定義した学習率の積を減算する。
h_0=\theta\\
h_t=h_{t-1}+(\nabla E)^2\\
\boldsymbol{w}^{(t+1)}=\boldsymbol{w}^{(t)}-\epsilon\frac{1}{\sqrt{h_t}+\theta}\nabla E
勾配の緩やかな斜面に対して、最適値に近づける。
学習率が徐々に小さくなるので、鞍点問題を引き起こすことがある。
RMSProp
誤差をパラメータで微分したものと再定義したもの学習率の積を減算する。
h_t=\alpha h_{t-1}+(1-\alpha)(\nabla E)^2\\
\boldsymbol{w}^{(t+1)}=\boldsymbol{w}^{(t)}-\epsilon\frac{1}{\sqrt{h_t}+\theta}\nabla E
局所的最適解にはならず、大域的最適解となり、ハイパーパラメータの調整が必要な場合が少ない。
Adam
- モメンタムの過去の勾配の指数関数的減衰平均
- RMSPropの過去の勾配の2乗の指数関数的減衰平均
上記をそれぞれ孕んだアルゴリズムである。
2.2 実装
各最適化手法の収束の様子を図に示す。
# 関数の定義
def numerical_gradient(f, x):
h = 1e-4
grad = np.zeros_like(x) # xと同じ形状の配列
for idx in range(x.size):
tmp_val = x[idx]
# f(x+h)の計算
x[idx] = tmp_val + h
fxh1 = f(x)
# f(x-h)の計算
x[idx] = tmp_val - h
fxh2 = f(x)
grad[idx] = (fxh1 - fxh2) / (2*h)
x[idx] = tmp_val # 値をもとに戻す
return grad
def gradient_descent(f, init_x, lr=0.01, step_num=100):
x = init_x
x_history = []
for i in range(step_num):
x_history.append(x.copy())
grad = numerical_gradient(f, x)
x -= lr * grad
return x, np.array(x_history)
def function(x):
return x[0]**2/20+x[1]**2
def calc_hist(optimizer, x_init):
params = {}
params['x0'] = x_init[0]
params['x1'] = x_init[1]
grads = {}
x_hist = []
grad = []
for _ in range(30):
x_hist.append(list(params.values()))
(grads['x0'], grads['x1']) = numerical_gradient(function, np.array(list(params.values())))
optimizer.update(params, grads)
return np.array(x_hist)
# データの準備
x = np.linspace(-10, 10, 21)
y = np.linspace(-5, 5, 11)
X, Y = np.meshgrid(x, y)
X = X.flatten()
Y = Y.flatten()
grad = np.array([numerical_gradient(function, np.array([x0, x1])) for x0, x1 in zip(X,Y)]).T
SGD
class SGD:
def __init__(self, lr=0.01):
self.lr = lr
def update(self, params, grads):
# paramsは重みパラメータ
# gradsは勾配
for key in params.keys():
params[key] -= self.lr * grads[key]
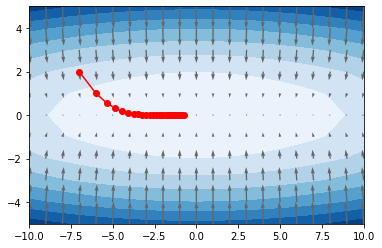
x_hist = calc_hist(SGD(lr=0.9), [-7.0, 2.0])
plt.contourf(X.reshape(11,21), Y.reshape(11,21), function(np.array([X, Y])).reshape(11,21), cmap='Blues');
plt.quiver(X, Y, -grad[0], -grad[1], angles="xy",color="#666666");
plt.plot(x_hist[:,0], x_hist[:,1], 'o-', color='red');
Momentum
class Momentum:
def __init__(self, lr=0.01, momentum=0.9):
self.lr = lr
self.momentum = momentum
self.v = None
def update(self, params, grads):
if self.v is None:
self.v = {}
for key, val in params.items():
# vの初期値は0行列
self.v[key] = np.zeros_like(val)
for key in params.keys():
self.v[key] = self.momentum*self.v[key] - self.lr*grads[key]
params[key] += self.v[key]
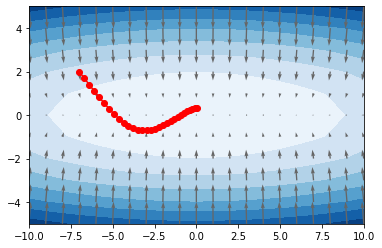
x_hist = calc_hist(Momentum(lr=0.09), [-7.0, 2.0])
plt.contourf(X.reshape(11,21), Y.reshape(11,21), function(np.array([X, Y])).reshape(11,21), cmap='Blues');
plt.quiver(X, Y, -grad[0], -grad[1], angles="xy",color="#666666");
plt.plot(x_hist[:,0], x_hist[:,1], 'o-', color='red');
AdaGrad
class AdaGrad:
def __init__(self, lr=0.01):
self.lr = lr
self.h = None
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] += grads[key] * grads[key]
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
x_hist = calc_hist(AdaGrad(lr=1.5), [-7.0, 2.0])
plt.contourf(X.reshape(11,21), Y.reshape(11,21), function(np.array([X, Y])).reshape(11,21), cmap='Blues');
plt.quiver(X, Y, -grad[0], -grad[1], angles="xy",color="#666666");
plt.plot(x_hist[:,0], x_hist[:,1], 'o-', color='red');
RMSprop
class RMSprop:
def __init__(self, lr=0.01, decay_rate=0.99):
self.lr = lr
self.decay_rate = decay_rate
self.h = None
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] *= self.decay_rate
self.h[key] += (1 - self.decay_rate) * grads[key] * grads[key]
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
x_hist = calc_hist(RMSprop(lr=0.1), [-7.0, 2.0])
plt.contourf(X.reshape(11,21), Y.reshape(11,21), function(np.array([X, Y])).reshape(11,21), cmap='Blues');
plt.quiver(X, Y, -grad[0], -grad[1], angles="xy",color="#666666");
plt.plot(x_hist[:,0], x_hist[:,1], 'o-', color='red');
Adam
class Adam:
def __init__(self, lr=0.001, rho1=0.9, rho2=0.999):
self.lr = lr
self.rho1 = rho1
self.rho2 = rho2
self.iter = 0
self.m = None
self.v = None
self.epsilon = 1e-8
def update(self, params, grads):
if self.m is None:
self.m, self.v = {}, {}
for key, val in params.items():
self.m[key] = np.zeros_like(val)
self.v[key] = np.zeros_like(val)
self.iter += 1
for key in params.keys():
self.m[key] = self.rho1*self.m[key] + (1-self.rho1)*grads[key]
self.v[key] = self.rho2*self.v[key] + (1-self.rho2)*(grads[key]**2)
m = self.m[key] / (1 - self.rho1**self.iter)
v = self.v[key] / (1 - self.rho2**self.iter)
params[key] -= self.lr * m / (np.sqrt(v) + self.epsilon)
x_hist = calc_hist(Adam(lr=0.3), [-7.0, 2.0])
plt.contourf(X.reshape(11,21), Y.reshape(11,21), function(np.array([X, Y])).reshape(11,21), cmap='Blues');
plt.quiver(X, Y, -grad[0], -grad[1], angles="xy",color="#666666");
plt.plot(x_hist[:,0], x_hist[:,1], 'o-', color='red');
次に、各最適化手法による学習の様子を示す。
SGD
from lesson_2.multi_layer_net import MultiLayerNet
# データの読み込み
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)
print("データ読み込み完了")
# batch_normalizationの設定 =======================
# use_batchnorm = True
use_batchnorm = False
# ====================================================
network = MultiLayerNet(input_size=784, hidden_size_list=[40, 20], output_size=10, activation='sigmoid', weight_init_std=0.01,
use_batchnorm=use_batchnorm)
iters_num = 1000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.01
train_loss_list = []
accuracies_train = []
accuracies_test = []
plot_interval=10
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
d_batch = d_train[batch_mask]
# 勾配
grad = network.gradient(x_batch, d_batch)
for key in ('W1', 'W2', 'W3', 'b1', 'b2', 'b3'):
network.params[key] -= learning_rate * grad[key]
loss = network.loss(x_batch, d_batch)
train_loss_list.append(loss)
if (i + 1) % plot_interval == 0:
accr_test = network.accuracy(x_test, d_test)
accuracies_test.append(accr_test)
accr_train = network.accuracy(x_batch, d_batch)
accuracies_train.append(accr_train)
if (i + 1) % 200 == 0:
print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
Momentum
# データの読み込み
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)
print("データ読み込み完了")
# batch_normalizationの設定 =======================
# use_batchnorm = True
use_batchnorm = False
# ====================================================
network = MultiLayerNet(input_size=784, hidden_size_list=[40, 20], output_size=10, activation='sigmoid', weight_init_std=0.01,
use_batchnorm=use_batchnorm)
iters_num = 1000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.3
# 慣性
momentum = 0.9
train_loss_list = []
accuracies_train = []
accuracies_test = []
plot_interval=10
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
d_batch = d_train[batch_mask]
# 勾配
grad = network.gradient(x_batch, d_batch)
if i == 0:
v = {}
for key in ('W1', 'W2', 'W3', 'b1', 'b2', 'b3'):
if i == 0:
v[key] = np.zeros_like(network.params[key])
v[key] = momentum * v[key] - learning_rate * grad[key]
network.params[key] += v[key]
loss = network.loss(x_batch, d_batch)
train_loss_list.append(loss)
if (i + 1) % plot_interval == 0:
accr_test = network.accuracy(x_test, d_test)
accuracies_test.append(accr_test)
accr_train = network.accuracy(x_batch, d_batch)
accuracies_train.append(accr_train)
if (i + 1) % 200 == 0:
print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
AdaGrad
# データの読み込み
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)
print("データ読み込み完了")
# batch_normalizationの設定 =======================
# use_batchnorm = True
use_batchnorm = False
# ====================================================
network = MultiLayerNet(input_size=784, hidden_size_list=[40, 20], output_size=10, activation='sigmoid', weight_init_std=0.01,
use_batchnorm=use_batchnorm)
iters_num = 1000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1
train_loss_list = []
accuracies_train = []
accuracies_test = []
plot_interval=10
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
d_batch = d_train[batch_mask]
# 勾配
grad = network.gradient(x_batch, d_batch)
if i == 0:
h = {}
for key in ('W1', 'W2', 'W3', 'b1', 'b2', 'b3'):
if i == 0:
h[key] = np.full_like(network.params[key], 1e-4)
else:
h[key] += np.square(grad[key])
network.params[key] -= learning_rate * grad[key] / (np.sqrt(h[key]))
loss = network.loss(x_batch, d_batch)
train_loss_list.append(loss)
if (i + 1) % plot_interval == 0:
accr_test = network.accuracy(x_test, d_test)
accuracies_test.append(accr_test)
accr_train = network.accuracy(x_batch, d_batch)
accuracies_train.append(accr_train)
if (i + 1) % 200 == 0:
print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
RMSprop
# データの読み込み
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)
print("データ読み込み完了")
# batch_normalizationの設定 =======================
# use_batchnorm = True
use_batchnorm = False
# ====================================================
network = MultiLayerNet(input_size=784, hidden_size_list=[40, 20], output_size=10, activation='sigmoid', weight_init_std=0.01,
use_batchnorm=use_batchnorm)
iters_num = 1000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.01
decay_rate = 0.99
train_loss_list = []
accuracies_train = []
accuracies_test = []
plot_interval=10
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
d_batch = d_train[batch_mask]
# 勾配
grad = network.gradient(x_batch, d_batch)
if i == 0:
h = {}
for key in ('W1', 'W2', 'W3', 'b1', 'b2', 'b3'):
if i == 0:
h[key] = np.zeros_like(network.params[key])
h[key] *= decay_rate
h[key] += (1 - decay_rate) * np.square(grad[key])
network.params[key] -= learning_rate * grad[key] / (np.sqrt(h[key]) + 1e-7)
loss = network.loss(x_batch, d_batch)
train_loss_list.append(loss)
if (i + 1) % plot_interval == 0:
accr_test = network.accuracy(x_test, d_test)
accuracies_test.append(accr_test)
accr_train = network.accuracy(x_batch, d_batch)
accuracies_train.append(accr_train)
if (i + 1) % 200 == 0:
print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
Adam
# データの読み込み
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)
print("データ読み込み完了")
# batch_normalizationの設定 =======================
# use_batchnorm = True
use_batchnorm = False
# ====================================================
network = MultiLayerNet(input_size=784, hidden_size_list=[40, 20], output_size=10, activation='sigmoid', weight_init_std=0.01,
use_batchnorm=use_batchnorm)
iters_num = 1000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.01
beta1 = 0.9
beta2 = 0.999
train_loss_list = []
accuracies_train = []
accuracies_test = []
plot_interval=10
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
d_batch = d_train[batch_mask]
# 勾配
grad = network.gradient(x_batch, d_batch)
if i == 0:
m = {}
v = {}
learning_rate_t = learning_rate * np.sqrt(1.0 - beta2 ** (i + 1)) / (1.0 - beta1 ** (i + 1))
for key in ('W1', 'W2', 'W3', 'b1', 'b2', 'b3'):
if i == 0:
m[key] = np.zeros_like(network.params[key])
v[key] = np.zeros_like(network.params[key])
m[key] += (1 - beta1) * (grad[key] - m[key])
v[key] += (1 - beta2) * (grad[key] ** 2 - v[key])
network.params[key] -= learning_rate_t * m[key] / (np.sqrt(v[key]) + 1e-7)
loss = network.loss(x_batch, d_batch)
train_loss_list.append(loss)
if (i + 1) % plot_interval == 0:
accr_test = network.accuracy(x_test, d_test)
accuracies_test.append(accr_test)
accr_train = network.accuracy(x_batch, d_batch)
accuracies_train.append(accr_train)
if (i + 1) % 200 == 0:
print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
3. 過学習
3.1 要約
テスト誤差と訓練誤差で学習曲線が乖離すること
ネットワークの自由度を制約する正則化を利用して抑制する
正則化手法
- L1正則化、L2正則化
- ドロップアウト
L1正則化、L2正則化
weight decay
過学習の原因: 重みが大きい値をとることで、過学習が発生することがある
過学習の解決策: 誤差に対して、正則化項を加算することで重みを抑制
誤差関数に、pノルムを加える
E_n(\boldsymbol{w})+\frac{1}{p}\lambda |\boldsymbol{x}|_p\\
|\boldsymbol{x}|_p=(|x_1|^p+\cdots+|x_n|^p)^{\frac{1}{p}}
p=1の場合、L1正則化
p=2の場合、L2正則化
ドロップアウト
ノードが多いと過学習の原因となるため、ランダムにノードを削除して学習させる。
データ量を変化させずに、異なるモデルを学習させていると解釈できる。
3.2 実装
まず、過学習の様子を再現する。
from common import optimizer
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True)
print("データ読み込み完了")
# 過学習を再現するために、学習データを削減
x_train = x_train[:300]
d_train = d_train[:300]
network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10)
optimizer = optimizer.SGD(learning_rate=0.01)
iters_num = 1000
train_size = x_train.shape[0]
batch_size = 100
train_loss_list = []
accuracies_train = []
accuracies_test = []
plot_interval=10
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
d_batch = d_train[batch_mask]
grad = network.gradient(x_batch, d_batch)
optimizer.update(network.params, grad)
loss = network.loss(x_batch, d_batch)
train_loss_list.append(loss)
if (i+1) % plot_interval == 0:
accr_train = network.accuracy(x_train, d_train)
accr_test = network.accuracy(x_test, d_test)
accuracies_train.append(accr_train)
accuracies_test.append(accr_test)
if (i + 1) % 200 == 0:
print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
L2正則化
from common import optimizer
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True)
print("データ読み込み完了")
# 過学習を再現するために、学習データを削減
x_train = x_train[:300]
d_train = d_train[:300]
network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10)
iters_num = 1000
train_size = x_train.shape[0]
batch_size = 100
learning_rate=0.01
train_loss_list = []
accuracies_train = []
accuracies_test = []
plot_interval=10
hidden_layer_num = network.hidden_layer_num
# 正則化強度設定 ======================================
weight_decay_lambda = 0.1
# =================================================
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
d_batch = d_train[batch_mask]
grad = network.gradient(x_batch, d_batch)
weight_decay = 0
for idx in range(1, hidden_layer_num+1):
grad['W' + str(idx)] = network.layers['Affine' + str(idx)].dW + weight_decay_lambda * network.params['W' + str(idx)]
grad['b' + str(idx)] = network.layers['Affine' + str(idx)].db
network.params['W' + str(idx)] -= learning_rate * grad['W' + str(idx)]
network.params['b' + str(idx)] -= learning_rate * grad['b' + str(idx)]
weight_decay += 0.5 * weight_decay_lambda * np.sqrt(np.sum(network.params['W' + str(idx)] ** 2))
loss = network.loss(x_batch, d_batch) + weight_decay
train_loss_list.append(loss)
if (i+1) % plot_interval == 0:
accr_train = network.accuracy(x_train, d_train)
accr_test = network.accuracy(x_test, d_test)
accuracies_train.append(accr_train)
accuracies_test.append(accr_test)
if (i + 1) % 200 == 0:
print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
L1正則化
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True)
print("データ読み込み完了")
# 過学習を再現するために、学習データを削減
x_train = x_train[:300]
d_train = d_train[:300]
network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10)
iters_num = 1000
train_size = x_train.shape[0]
batch_size = 100
learning_rate=0.1
train_loss_list = []
accuracies_train = []
accuracies_test = []
plot_interval=10
hidden_layer_num = network.hidden_layer_num
# 正則化強度設定 ======================================
weight_decay_lambda = 0.005
# =================================================
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
d_batch = d_train[batch_mask]
grad = network.gradient(x_batch, d_batch)
weight_decay = 0
for idx in range(1, hidden_layer_num+1):
grad['W' + str(idx)] = network.layers['Affine' + str(idx)].dW + weight_decay_lambda * np.sign(network.params['W' + str(idx)])
grad['b' + str(idx)] = network.layers['Affine' + str(idx)].db
network.params['W' + str(idx)] -= learning_rate * grad['W' + str(idx)]
network.params['b' + str(idx)] -= learning_rate * grad['b' + str(idx)]
weight_decay += weight_decay_lambda * np.sum(np.abs(network.params['W' + str(idx)]))
loss = network.loss(x_batch, d_batch) + weight_decay
train_loss_list.append(loss)
if (i+1) % plot_interval == 0:
accr_train = network.accuracy(x_train, d_train)
accr_test = network.accuracy(x_test, d_test)
accuracies_train.append(accr_train)
accuracies_test.append(accr_test)
if (i + 1) % 200 == 0:
print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
L2正則化の正則化強度を変えて結果を確認
from common import optimizer
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True)
print("データ読み込み完了")
# 過学習を再現するために、学習データを削減
x_train = x_train[:300]
d_train = d_train[:300]
network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10)
iters_num = 1000
train_size = x_train.shape[0]
batch_size = 100
learning_rate=0.01
train_loss_list = []
accuracies_train = []
accuracies_test = []
plot_interval=10
hidden_layer_num = network.hidden_layer_num
# 正則化強度設定 ======================================
weight_decay_lambda = 0.12
# =================================================
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
d_batch = d_train[batch_mask]
grad = network.gradient(x_batch, d_batch)
weight_decay = 0
for idx in range(1, hidden_layer_num+1):
grad['W' + str(idx)] = network.layers['Affine' + str(idx)].dW + weight_decay_lambda * network.params['W' + str(idx)]
grad['b' + str(idx)] = network.layers['Affine' + str(idx)].db
network.params['W' + str(idx)] -= learning_rate * grad['W' + str(idx)]
network.params['b' + str(idx)] -= learning_rate * grad['b' + str(idx)]
weight_decay += 0.5 * weight_decay_lambda * np.sqrt(np.sum(network.params['W' + str(idx)] ** 2))
loss = network.loss(x_batch, d_batch) + weight_decay
train_loss_list.append(loss)
if (i+1) % plot_interval == 0:
accr_train = network.accuracy(x_train, d_train)
accr_test = network.accuracy(x_test, d_test)
accuracies_train.append(accr_train)
accuracies_test.append(accr_test)
if (i + 1) % 200 == 0:
print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
Dropout
class Dropout:
def __init__(self, dropout_ratio=0.5):
self.dropout_ratio = dropout_ratio
self.mask = None
def forward(self, x, train_flg=True):
if train_flg:
self.mask = np.random.rand(*x.shape) > self.dropout_ratio
return x * self.mask
else:
return x * (1.0 - self.dropout_ratio)
def backward(self, dout):
return dout * self.mask
from common import optimizer
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True)
print("データ読み込み完了")
# 過学習を再現するために、学習データを削減
x_train = x_train[:300]
d_train = d_train[:300]
# ドロップアウト設定 ======================================
use_dropout = True
dropout_ratio = 0.01
# ====================================================
network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10,
weight_decay_lambda=weight_decay_lambda, use_dropout = use_dropout, dropout_ratio = dropout_ratio)
optimizer = optimizer.SGD(learning_rate=0.01)
# optimizer = optimizer.Momentum(learning_rate=0.01, momentum=0.9)
# optimizer = optimizer.AdaGrad(learning_rate=0.01)
# optimizer = optimizer.Adam()
iters_num = 1000
train_size = x_train.shape[0]
batch_size = 100
train_loss_list = []
accuracies_train = []
accuracies_test = []
plot_interval=10
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
d_batch = d_train[batch_mask]
grad = network.gradient(x_batch, d_batch)
optimizer.update(network.params, grad)
loss = network.loss(x_batch, d_batch)
train_loss_list.append(loss)
if (i+1) % plot_interval == 0:
accr_train = network.accuracy(x_train, d_train)
accr_test = network.accuracy(x_test, d_test)
accuracies_train.append(accr_train)
accuracies_test.append(accr_test)
if (i + 1) % 200 == 0:
print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
Dropoutの確率を変化させて確認
from common import optimizer
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True)
print("データ読み込み完了")
# 過学習を再現するために、学習データを削減
x_train = x_train[:300]
d_train = d_train[:300]
# ドロップアウト設定 ======================================
use_dropout = True
dropout_ratio = 0.005
# ====================================================
network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10,
weight_decay_lambda=weight_decay_lambda, use_dropout = use_dropout, dropout_ratio = dropout_ratio)
optimizer = optimizer.SGD(learning_rate=0.01)
# optimizer = optimizer.Momentum(learning_rate=0.01, momentum=0.9)
# optimizer = optimizer.AdaGrad(learning_rate=0.01)
# optimizer = optimizer.Adam()
iters_num = 1000
train_size = x_train.shape[0]
batch_size = 100
train_loss_list = []
accuracies_train = []
accuracies_test = []
plot_interval=10
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
d_batch = d_train[batch_mask]
grad = network.gradient(x_batch, d_batch)
optimizer.update(network.params, grad)
loss = network.loss(x_batch, d_batch)
train_loss_list.append(loss)
if (i+1) % plot_interval == 0:
accr_train = network.accuracy(x_train, d_train)
accr_test = network.accuracy(x_test, d_test)
accuracies_train.append(accr_train)
accuracies_test.append(accr_test)
if (i + 1) % 200 == 0:
print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
3.3 確認テスト
リッジ回帰の特徴は、
a. ハイパーパラメータを大きな値に設定すると、すべての重みが限りなく0に近づく
4. 畳み込みニューラルネットワーク
4.1 要約
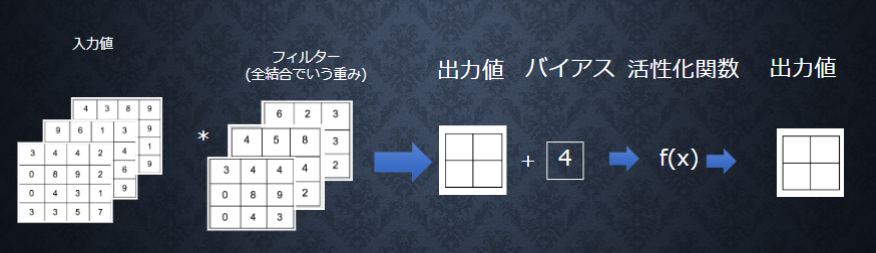
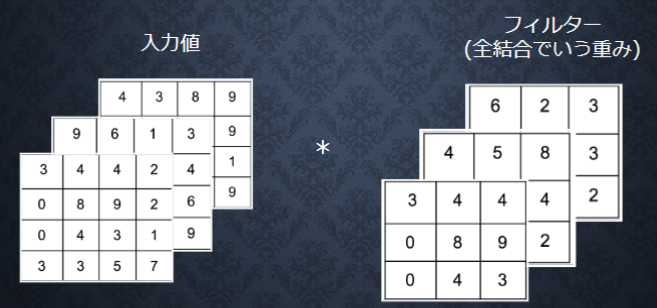
畳み込み層
画像の場合、縦・横・チャンネルの3次元データをそのまま学習し、次に伝えることができる。
畳み込み層の全体層を図に示す。
パディング
入力データの周囲に固定のデータを埋めること。
畳み込み処理をするとデータのサイズが小さくなるため、入出力でデータのサイズを保つために行われる。
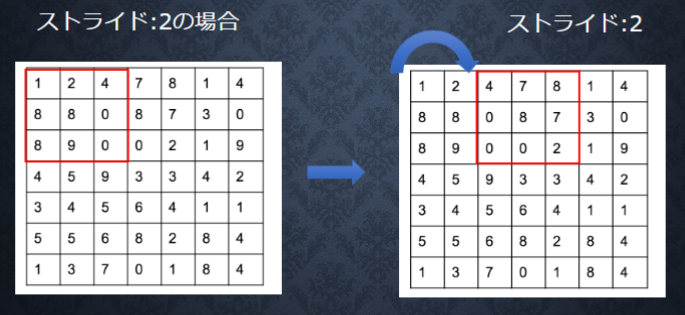
ストライド
フィルタを適用する位置の間隔のこと。
ストライドが大きくなると出力サイズは小さくなる。
ここで、入力サイズを$(H,W)$、フィルタサイズを$(FH,FW)$、出力サイズを$(OH,OW)$、パディングをP、ストライドをSとする。
出力サイズは、
OH=\frac{H+2P-FH}{S}+1\\
OW=\frac{W+2P-FW}{S}+1
チャンネル
プーリング層
例えば「2×2」の領域に対して、最大となる要素を取り出すような処理をプーリングと呼ぶ。
例のように最大値を取り出す場合Maxプーリング、平均値の場合はAverageプーリングと呼ぶ。
一般的にプーリングのウィンドウサイズと、ストライドは同じ値に設定する。
プーリング層には、
- 学習するパラメータがない
- チャンネル数は変化しない
- 微小な位置変化に対してロバスト
などの特徴がある。
4.2 実装
im2colという関数を定義する。
これは4次元のデータを2次元に変換する関数である。
入力データに対してフィルタを適用する場所の領域(3次元ブロック)を横方向に1列に展開する。
この展開処理を、フィルタを適用するすべての場所で行う。
フィルタは縦方向に1列に展開して並べ、im2colで変換したデータと行列の積を計算し、出力データのサイズに変換する。
# 画像データを2次元配列に変換
'''
input_data: 入力値
filter_h: フィルターの高さ
filter_w: フィルターの横幅
stride: ストライド
pad: パディング
'''
def im2col(input_data, filter_h, filter_w, stride=1, pad=0):
# N: number, C: channel, H: height, W: width
N, C, H, W = input_data.shape
out_h = (H + 2 * pad - filter_h)//stride + 1
out_w = (W + 2 * pad - filter_w)//stride + 1
img = np.pad(input_data, [(0,0), (0,0), (pad, pad), (pad, pad)], 'constant')
col = np.zeros((N, C, filter_h, filter_w, out_h, out_w))
for y in range(filter_h):
y_max = y + stride * out_h
for x in range(filter_w):
x_max = x + stride * out_w
col[:, :, y, x, :, :] = img[:, :, y:y_max:stride, x:x_max:stride]
col = col.transpose(0, 4, 5, 1, 2, 3) # (N, C, filter_h, filter_w, out_h, out_w) -> (N, filter_w, out_h, out_w, C, filter_h)
col = col.reshape(N * out_h * out_w, -1)
return col
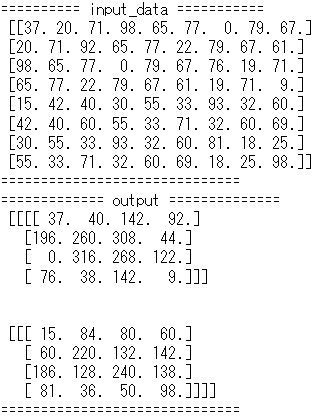
# im2colの処理確認
input_data = np.random.rand(2, 1, 4, 4)*100//1 # number, channel, height, widthを表す
print('========== input_data ===========\n', input_data)
print('==============================')
filter_h = 3
filter_w = 3
stride = 1
pad = 0
col = im2col(input_data, filter_h=filter_h, filter_w=filter_w, stride=stride, pad=pad)
print('============= col ==============\n', col)
print('==============================')
# 2次元配列を画像データに変換
def col2im(col, input_shape, filter_h, filter_w, stride=1, pad=0):
# N: number, C: channel, H: height, W: width
N, C, H, W = input_shape
# 切り捨て除算
out_h = (H + 2 * pad - filter_h)//stride + 1
out_w = (W + 2 * pad - filter_w)//stride + 1
col = col.reshape(N, out_h, out_w, C, filter_h, filter_w).transpose(0, 3, 4, 5, 1, 2) # (N, filter_h, filter_w, out_h, out_w, C)
img = np.zeros((N, C, H + 2 * pad + stride - 1, W + 2 * pad + stride - 1))
for y in range(filter_h):
y_max = y + stride * out_h
for x in range(filter_w):
x_max = x + stride * out_w
img[:, :, y:y_max:stride, x:x_max:stride] += col[:, :, y, x, :, :]
return img[:, :, pad:H + pad, pad:W + pad]
# im2colの処理確認
print('========== input_data ===========\n', col)
print('==============================')
filter_h = 3
filter_w = 3
stride = 1
pad = 0
output = col2im(col, input_shape=input_data.shape, filter_h=filter_h, filter_w=filter_w, stride=stride, pad=pad)
print('============= output ==============\n', output)
print('==============================')
畳み込み層の実装
1層の畳み込み演算を行う。
class Convolution:
# W: フィルター, b: バイアス
def __init__(self, W, b, stride=1, pad=0):
self.W = W
self.b = b
self.stride = stride
self.pad = pad
# 中間データ(backward時に使用)
self.x = None
self.col = None
self.col_W = None
# フィルター・バイアスパラメータの勾配
self.dW = None
self.db = None
def forward(self, x):
# FN: filter_number, C: channel, FH: filter_height, FW: filter_width
FN, C, FH, FW = self.W.shape
N, C, H, W = x.shape
# 出力値のheight, width
out_h = 1 + int((H + 2 * self.pad - FH) / self.stride)
out_w = 1 + int((W + 2 * self.pad - FW) / self.stride)
# xを行列に変換
col = im2col(x, FH, FW, self.stride, self.pad)
# フィルターをxに合わせた行列に変換
col_W = self.W.reshape(FN, -1).T
out = np.dot(col, col_W) + self.b
# 計算のために変えた形式を戻す
out = out.reshape(N, out_h, out_w, -1).transpose(0, 3, 1, 2)
self.x = x
self.col = col
self.col_W = col_W
return out
def backward(self, dout):
FN, C, FH, FW = self.W.shape
dout = dout.transpose(0, 2, 3, 1).reshape(-1, FN)
self.db = np.sum(dout, axis=0)
self.dW = np.dot(self.col.T, dout)
self.dW = self.dW.transpose(1, 0).reshape(FN, C, FH, FW)
dcol = np.dot(dout, self.col_W.T)
# dcolを画像データに変換
dx = col2im(dcol, self.x.shape, FH, FW, self.stride, self.pad)
return dx
Poolingの実装は以下の流れで行う。
- 入力データを展開する
- 行ごとに最大値を求める
- 適切な出力サイズに整形する
class Pooling:
def __init__(self, pool_h, pool_w, stride=1, pad=0):
self.pool_h = pool_h
self.pool_w = pool_w
self.stride = stride
self.pad = pad
self.x = None
self.arg_max = None
def forward(self, x):
N, C, H, W = x.shape
out_h = int(1 + (H - self.pool_h) / self.stride)
out_w = int(1 + (W - self.pool_w) / self.stride)
# xを行列に変換
col = im2col(x, self.pool_h, self.pool_w, self.stride, self.pad)
# プーリングのサイズに合わせてリサイズ
col = col.reshape(-1, self.pool_h*self.pool_w)
# 行ごとに最大値を求める
arg_max = np.argmax(col, axis=1)
out = np.max(col, axis=1)
# 整形
out = out.reshape(N, out_h, out_w, C).transpose(0, 3, 1, 2)
self.x = x
self.arg_max = arg_max
return out
def backward(self, dout):
dout = dout.transpose(0, 2, 3, 1)
pool_size = self.pool_h * self.pool_w
dmax = np.zeros((dout.size, pool_size))
dmax[np.arange(self.arg_max.size), self.arg_max.flatten()] = dout.flatten()
dmax = dmax.reshape(dout.shape + (pool_size,))
dcol = dmax.reshape(dmax.shape[0] * dmax.shape[1] * dmax.shape[2], -1)
dx = col2im(dcol, self.x.shape, self.pool_h, self.pool_w, self.stride, self.pad)
return dx
class SimpleConvNet:
# conv - relu - pool - affine - relu - affine - softmax
def __init__(self, input_dim=(1, 28, 28), conv_param={'filter_num':30, 'filter_size':5, 'pad':0, 'stride':1},
hidden_size=100, output_size=10, weight_init_std=0.01):
filter_num = conv_param['filter_num']
filter_size = conv_param['filter_size']
filter_pad = conv_param['pad']
filter_stride = conv_param['stride']
input_size = input_dim[1]
conv_output_size = (input_size - filter_size + 2 * filter_pad) / filter_stride + 1
pool_output_size = int(filter_num * (conv_output_size / 2) * (conv_output_size / 2))
# 重みの初期化
self.params = {}
self.params['W1'] = weight_init_std * np.random.randn(filter_num, input_dim[0], filter_size, filter_size)
self.params['b1'] = np.zeros(filter_num)
self.params['W2'] = weight_init_std * np.random.randn(pool_output_size, hidden_size)
self.params['b2'] = np.zeros(hidden_size)
self.params['W3'] = weight_init_std * np.random.randn(hidden_size, output_size)
self.params['b3'] = np.zeros(output_size)
# レイヤの生成
self.layers = OrderedDict()
self.layers['Conv1'] = layers.Convolution(self.params['W1'], self.params['b1'], conv_param['stride'], conv_param['pad'])
self.layers['Relu1'] = layers.Relu()
self.layers['Pool1'] = layers.Pooling(pool_h=2, pool_w=2, stride=2)
self.layers['Affine1'] = layers.Affine(self.params['W2'], self.params['b2'])
self.layers['Relu2'] = layers.Relu()
self.layers['Affine2'] = layers.Affine(self.params['W3'], self.params['b3'])
self.last_layer = layers.SoftmaxWithLoss()
def predict(self, x):
for key in self.layers.keys():
x = self.layers[key].forward(x)
return x
def loss(self, x, d):
y = self.predict(x)
return self.last_layer.forward(y, d)
def accuracy(self, x, d, batch_size=100):
if d.ndim != 1 : d = np.argmax(d, axis=1)
acc = 0.0
for i in range(int(x.shape[0] / batch_size)):
tx = x[i*batch_size:(i+1)*batch_size]
td = d[i*batch_size:(i+1)*batch_size]
y = self.predict(tx)
y = np.argmax(y, axis=1)
acc += np.sum(y == td)
return acc / x.shape[0]
def gradient(self, x, d):
# forward
self.loss(x, d)
# backward
dout = 1
dout = self.last_layer.backward(dout)
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
# 設定
grad = {}
grad['W1'], grad['b1'] = self.layers['Conv1'].dW, self.layers['Conv1'].db
grad['W2'], grad['b2'] = self.layers['Affine1'].dW, self.layers['Affine1'].db
grad['W3'], grad['b3'] = self.layers['Affine2'].dW, self.layers['Affine2'].db
return grad
def save_params(self, file_name="params.pkl"):
params = {}
for key, val in self.params.items():
params[key] = val
with open(file_name, 'wb') as f:
pickle.dump(params, f)
def load_params(self, file_name="params.pkl"):
with open(file_name, 'rb') as f:
params = pickle.load(f)
for key, val in params.items():
self.params[key] = val
for i, key in enumerate(['Conv1', 'Affine1', 'Affine2']):
self.layers[key].W = self.params['W' + str(i+1)]
self.layers[key].b = self.params['b' + str(i+1)]
from common import optimizer
# データの読み込み
(x_train, d_train), (x_test, d_test) = load_mnist(flatten=False)
print("データ読み込み完了")
# 処理に時間のかかる場合はデータを削減
x_train, d_train = x_train[::20], d_train[::20]
x_test, d_test = x_test[::20], d_test[::20]
network = SimpleConvNet(input_dim=(1,28,28), conv_param = {'filter_num': 30, 'filter_size': 5, 'pad': 0, 'stride': 1},
hidden_size=100, output_size=10, weight_init_std=0.01)
optimizer = optimizer.Adam()
iters_num = 1000
train_size = x_train.shape[0]
batch_size = 100
train_loss_list = []
accuracies_train = []
accuracies_test = []
plot_interval=10
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
d_batch = d_train[batch_mask]
grad = network.gradient(x_batch, d_batch)
optimizer.update(network.params, grad)
loss = network.loss(x_batch, d_batch)
train_loss_list.append(loss)
if (i+1) % plot_interval == 0:
accr_train = network.accuracy(x_train, d_train)
accr_test = network.accuracy(x_test, d_test)
accuracies_train.append(accr_train)
accuracies_test.append(accr_test)
if (i + 1) % 200 == 0:
print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
def filter_show(filters, nx=8, margin=3, scale=10):
"""
c.f. https://gist.github.com/aidiary/07d530d5e08011832b12#file-draw_weight-py
"""
FN, C, FH, FW = filters.shape
ny = int(np.ceil(FN / nx))
fig = plt.figure()
fig.subplots_adjust(left=0, right=1, bottom=0, top=1, hspace=0.05, wspace=0.05)
for i in range(FN):
ax = fig.add_subplot(ny, nx, i+1, xticks=[], yticks=[])
ax.imshow(filters[i, 0], cmap=plt.cm.gray_r, interpolation='nearest')
plt.show()
network = SimpleConvNet()
# ランダム初期化後の重み
filter_show(network.params['W1'])
# 学習後の重み
network.load_params("params.pkl")
filter_show(network.params['W1'])
2層畳み込みネットワークの実装を行う。
class DoubleConvNet:
# conv - relu - pool - conv - relu - pool - affine - relu - affine - softmax
def __init__(self, input_dim=(1, 28, 28),
conv_param_1={'filter_num':10, 'filter_size':7, 'pad':1, 'stride':1},
conv_param_2={'filter_num':20, 'filter_size':3, 'pad':1, 'stride':1},
hidden_size=100, output_size=10, weight_init_std=0.01):
conv_output_size_1 = (input_dim[1] - conv_param_1['filter_size'] + 2 * conv_param_1['pad']) / conv_param_1['stride'] + 1
conv_output_size_2 = (conv_output_size_1 / 2 - conv_param_2['filter_size'] + 2 * conv_param_2['pad']) / conv_param_2['stride'] + 1
pool_output_size = int(conv_param_2['filter_num'] * (conv_output_size_2 / 2) * (conv_output_size_2 / 2))
# 重みの初期化
self.params = {}
self.params['W1'] = weight_init_std * np.random.randn(conv_param_1['filter_num'], input_dim[0], conv_param_1['filter_size'], conv_param_1['filter_size'])
self.params['b1'] = np.zeros(conv_param_1['filter_num'])
self.params['W2'] = weight_init_std * np.random.randn(conv_param_2['filter_num'], conv_param_1['filter_num'], conv_param_2['filter_size'], conv_param_2['filter_size'])
self.params['b2'] = np.zeros(conv_param_2['filter_num'])
self.params['W3'] = weight_init_std * np.random.randn(pool_output_size, hidden_size)
self.params['b3'] = np.zeros(hidden_size)
self.params['W4'] = weight_init_std * np.random.randn(hidden_size, output_size)
self.params['b4'] = np.zeros(output_size)
# レイヤの生成
self.layers = OrderedDict()
self.layers['Conv1'] = layers.Convolution(self.params['W1'], self.params['b1'], conv_param_1['stride'], conv_param_1['pad'])
self.layers['Relu1'] = layers.Relu()
self.layers['Pool1'] = layers.Pooling(pool_h=2, pool_w=2, stride=2)
self.layers['Conv2'] = layers.Convolution(self.params['W2'], self.params['b2'], conv_param_2['stride'], conv_param_2['pad'])
self.layers['Relu2'] = layers.Relu()
self.layers['Pool2'] = layers.Pooling(pool_h=2, pool_w=2, stride=2)
self.layers['Affine1'] = layers.Affine(self.params['W3'], self.params['b3'])
self.layers['Relu3'] = layers.Relu()
self.layers['Affine2'] = layers.Affine(self.params['W4'], self.params['b4'])
self.last_layer = layers.SoftmaxWithLoss()
def predict(self, x):
for key in self.layers.keys():
x = self.layers[key].forward(x)
return x
def loss(self, x, d):
y = self.predict(x)
return self.last_layer.forward(y, d)
def accuracy(self, x, d, batch_size=100):
if d.ndim != 1 : d = np.argmax(d, axis=1)
acc = 0.0
for i in range(int(x.shape[0] / batch_size)):
tx = x[i*batch_size:(i+1)*batch_size]
td = d[i*batch_size:(i+1)*batch_size]
y = self.predict(tx)
y = np.argmax(y, axis=1)
acc += np.sum(y == td)
return acc / x.shape[0]
def gradient(self, x, d):
# forward
self.loss(x, d)
# backward
dout = 1
dout = self.last_layer.backward(dout)
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
# 設定
grad = {}
grad['W1'], grad['b1'] = self.layers['Conv1'].dW, self.layers['Conv1'].db
grad['W2'], grad['b2'] = self.layers['Conv2'].dW, self.layers['Conv2'].db
grad['W3'], grad['b3'] = self.layers['Affine1'].dW, self.layers['Affine1'].db
grad['W4'], grad['b4'] = self.layers['Affine2'].dW, self.layers['Affine2'].db
return grad
from common import optimizer
# データの読み込み
(x_train, d_train), (x_test, d_test) = load_mnist(flatten=False)
print("データ読み込み完了")
# 処理に時間のかかる場合はデータを削減
x_train, d_train = x_train[::20], d_train[::20]
x_test, d_test = x_test[::20], d_test[::20]
network = DoubleConvNet(input_dim=(1,28,28),
conv_param_1={'filter_num':10, 'filter_size':7, 'pad':1, 'stride':1},
conv_param_2={'filter_num':20, 'filter_size':3, 'pad':1, 'stride':1},
hidden_size=100, output_size=10, weight_init_std=0.01)
optimizer = optimizer.Adam()
# 時間がかかるため100に設定
iters_num = 100
# iters_num = 1000
train_size = x_train.shape[0]
batch_size = 100
train_loss_list = []
accuracies_train = []
accuracies_test = []
plot_interval=10
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
d_batch = d_train[batch_mask]
grad = network.gradient(x_batch, d_batch)
optimizer.update(network.params, grad)
loss = network.loss(x_batch, d_batch)
train_loss_list.append(loss)
if (i+1) % plot_interval == 0:
accr_train = network.accuracy(x_train, d_train)
accr_test = network.accuracy(x_test, d_test)
accuracies_train.append(accr_train)
accuracies_test.append(accr_test)
if (i + 1) % 200 == 0:
print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
より深いネットワークの実装を行う。
class DeepConvNet:
'''
認識率99%以上の高精度なConvNet
conv - relu - conv- relu - pool -
conv - relu - conv- relu - pool -
conv - relu - conv- relu - pool -
affine - relu - dropout - affine - dropout - softmax
'''
def __init__(self, input_dim=(1, 28, 28),
conv_param_1 = {'filter_num':16, 'filter_size':3, 'pad':1, 'stride':1},
conv_param_2 = {'filter_num':16, 'filter_size':3, 'pad':1, 'stride':1},
conv_param_3 = {'filter_num':32, 'filter_size':3, 'pad':1, 'stride':1},
conv_param_4 = {'filter_num':32, 'filter_size':3, 'pad':2, 'stride':1},
conv_param_5 = {'filter_num':64, 'filter_size':3, 'pad':1, 'stride':1},
conv_param_6 = {'filter_num':64, 'filter_size':3, 'pad':1, 'stride':1},
hidden_size=50, output_size=10):
# 重みの初期化===========
# 各層のニューロンひとつあたりが、前層のニューロンといくつのつながりがあるか
pre_node_nums = np.array([1*3*3, 16*3*3, 16*3*3, 32*3*3, 32*3*3, 64*3*3, 64*4*4, hidden_size])
wight_init_scales = np.sqrt(2.0 / pre_node_nums) # Heの初期値
self.params = {}
pre_channel_num = input_dim[0]
for idx, conv_param in enumerate([conv_param_1, conv_param_2, conv_param_3, conv_param_4, conv_param_5, conv_param_6]):
self.params['W' + str(idx+1)] = wight_init_scales[idx] * np.random.randn(conv_param['filter_num'], pre_channel_num, conv_param['filter_size'], conv_param['filter_size'])
self.params['b' + str(idx+1)] = np.zeros(conv_param['filter_num'])
pre_channel_num = conv_param['filter_num']
self.params['W7'] = wight_init_scales[6] * np.random.randn(pre_node_nums[6], hidden_size)
print(self.params['W7'].shape)
self.params['b7'] = np.zeros(hidden_size)
self.params['W8'] = wight_init_scales[7] * np.random.randn(pre_node_nums[7], output_size)
self.params['b8'] = np.zeros(output_size)
# レイヤの生成===========
self.layers = []
self.layers.append(layers.Convolution(self.params['W1'], self.params['b1'],
conv_param_1['stride'], conv_param_1['pad']))
self.layers.append(layers.Relu())
self.layers.append(layers.Convolution(self.params['W2'], self.params['b2'],
conv_param_2['stride'], conv_param_2['pad']))
self.layers.append(layers.Relu())
self.layers.append(layers.Pooling(pool_h=2, pool_w=2, stride=2))
self.layers.append(layers.Convolution(self.params['W3'], self.params['b3'],
conv_param_3['stride'], conv_param_3['pad']))
self.layers.append(layers.Relu())
self.layers.append(layers.Convolution(self.params['W4'], self.params['b4'],
conv_param_4['stride'], conv_param_4['pad']))
self.layers.append(layers.Relu())
self.layers.append(layers.Pooling(pool_h=2, pool_w=2, stride=2))
self.layers.append(layers.Convolution(self.params['W5'], self.params['b5'],
conv_param_5['stride'], conv_param_5['pad']))
self.layers.append(layers.Relu())
self.layers.append(layers.Convolution(self.params['W6'], self.params['b6'],
conv_param_6['stride'], conv_param_6['pad']))
self.layers.append(layers.Relu())
self.layers.append(layers.Pooling(pool_h=2, pool_w=2, stride=2))
self.layers.append(layers.Affine(self.params['W7'], self.params['b7']))
self.layers.append(layers.Relu())
self.layers.append(layers.Dropout(0.5))
self.layers.append(layers.Affine(self.params['W8'], self.params['b8']))
self.layers.append(layers.Dropout(0.5))
self.last_layer = layers.SoftmaxWithLoss()
def predict(self, x, train_flg=False):
for layer in self.layers:
if isinstance(layer, layers.Dropout):
x = layer.forward(x, train_flg)
else:
x = layer.forward(x)
return x
def loss(self, x, d):
y = self.predict(x, train_flg=True)
return self.last_layer.forward(y, d)
def accuracy(self, x, d, batch_size=100):
if d.ndim != 1 : d = np.argmax(d, axis=1)
acc = 0.0
for i in range(int(x.shape[0] / batch_size)):
tx = x[i*batch_size:(i+1)*batch_size]
td = d[i*batch_size:(i+1)*batch_size]
y = self.predict(tx, train_flg=False)
y = np.argmax(y, axis=1)
acc += np.sum(y == td)
return acc / x.shape[0]
def gradient(self, x, d):
# forward
self.loss(x, d)
# backward
dout = 1
dout = self.last_layer.backward(dout)
tmp_layers = self.layers.copy()
tmp_layers.reverse()
for layer in tmp_layers:
dout = layer.backward(dout)
# 設定
grads = {}
for i, layer_idx in enumerate((0, 2, 5, 7, 10, 12, 15, 18)):
grads['W' + str(i+1)] = self.layers[layer_idx].dW
grads['b' + str(i+1)] = self.layers[layer_idx].db
return grads
from common import optimizer
(x_train, d_train), (x_test, d_test) = load_mnist(flatten=False)
# 処理に時間のかかる場合はデータを削減
x_train, d_train = x_train[::20], d_train[::20]
x_test, d_test = x_test[::20], d_test[::20]
print("データ読み込み完了")
network = DeepConvNet()
optimizer = optimizer.Adam()
iters_num = 1000
train_size = x_train.shape[0]
batch_size = 100
train_loss_list = []
accuracies_train = []
accuracies_test = []
plot_interval=10
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
d_batch = d_train[batch_mask]
grad = network.gradient(x_batch, d_batch)
optimizer.update(network.params, grad)
loss = network.loss(x_batch, d_batch)
train_loss_list.append(loss)
if (i+1) % plot_interval == 0:
accr_train = network.accuracy(x_train, d_train)
accr_test = network.accuracy(x_test, d_test)
accuracies_train.append(accr_train)
accuracies_test.append(accr_test)
if (i + 1) % 200 == 0:
print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
4.3 確認テスト
サイズ6×6の入力画像を、サイズ2×2のフィルタで畳み込んだ時の出力画像のサイズ
ストライドとパディングは1とする.
(6+2×1-2)/1=6
出力画像は6×6となる
5.1 要約
AlexNetモデル
構造は次のようになっている。
-
入力:224 x 224に正規化した,3チャンネルカラー画像
-
畳み込み層 – カーネル11 x 11 x 96チャンネル, stride = 4, padding = 2
-
活性化関数: ReLU
-
プーリング層 – 重なりあり最大値プーリング, カーネル3 x 3, stride = 2
-
畳み込み層 – カーネル5 x 5 x 256チャンネル, stride = 1, padding = 2
-
活性化関数: ReLU
-
プーリング層 – 重なりあり最大値プーリング, [3 x 3]カーネル, stride = 2
-
畳み込み層 – カーネル3 x 3 x 384チャンネル, stride = 1, padding = 1
-
畳み込み層 – カーネル3 x 3 x 384チャンネル, stride = 1, padding = 1
-
畳み込み層 – カーネル3 x 3 x 256チャンネル, stride = 1, padding = 1
-
プーリング層 – 重なりあり最大値プーリング, [3 x 3]カーネル, stride = 2
-
Dropout
-
全結合層 – 9216 (=256 x 6 x 6) v.s. 4096
-
活性化関数: ReLU
-
Dropout
-
全結合層 – 4096 v.s. 4096
-
活性化関数: ReLU
-
全結合層 – 4096 v.s. 1000
-
出力:softmax関数で確率化した1000次元ベクトル
5.2 実装
class AlexNet:
'''
conv - relu - pool - conv - relu - pool -
conv - conv - conv - pool -
- dropout - affine - relu - dropout - affine - relu - affine - softmax
'''
def __init__(self, input_dim=(1, 28, 28),
conv_param_1 = {'filter_num':96, 'filter_size':11, 'pad':2, 'stride':4},
conv_param_2 = {'filter_num':256, 'filter_size':5, 'pad':2, 'stride':1},
conv_param_3 = {'filter_num':384, 'filter_size':3, 'pad':1, 'stride':1},
conv_param_4 = {'filter_num':384, 'filter_size':3, 'pad':1, 'stride':1},
conv_param_5 = {'filter_num':256, 'filter_size':3, 'pad':1, 'stride':1},
hidden_size=4096, output_size=10):
# 重みの初期化===========
# 各層のニューロンひとつあたりが、前層のニューロンといくつのつながりがあるか
pre_node_nums = np.array([1*3*3, 96*11*11, 256*5*5, 96*3*3, 96*3*3, 96*3*3, 9216, 4096, 4096, hidden_size])
wight_init_scales = np.sqrt(2.0 / pre_node_nums) # Heの初期値
self.params = {}
pre_channel_num = input_dim[0]
for idx, conv_param in enumerate([conv_param_1, conv_param_2, conv_param_3, conv_param_4, conv_param_5]):
self.params['W' + str(idx+1)] = wight_init_scales[idx] * np.random.randn(conv_param['filter_num'], pre_channel_num, conv_param['filter_size'], conv_param['filter_size'])
self.params['b' + str(idx+1)] = np.zeros(conv_param['filter_num'])
pre_channel_num = conv_param['filter_num']
self.params['W6'] = wight_init_scales[6] * np.random.randn(pre_node_nums[6], hidden_size)
self.params['b6'] = np.zeros(hidden_size)
self.params['W7'] = wight_init_scales[7] * np.random.randn(pre_node_nums[7], hidden_size)
self.params['b7'] = np.zeros(hidden_size)
self.params['W8'] = wight_init_scales[8] * np.random.randn(pre_node_nums[8], output_size)
self.params['b8'] = np.zeros(output_size)
# レイヤの生成===========
self.layers = []
self.layers.append(layers.Convolution(self.params['W1'], self.params['b1'],
conv_param_1['stride'], conv_param_1['pad']))
self.layers.append(layers.Relu())
self.layers.append(layers.Pooling(pool_h=3, pool_w=3, stride=2))
self.layers.append(layers.Convolution(self.params['W2'], self.params['b2'],
conv_param_2['stride'], conv_param_2['pad']))
self.layers.append(layers.Relu())
self.layers.append(layers.Pooling(pool_h=3, pool_w=3, stride=2))
self.layers.append(layers.Convolution(self.params['W3'], self.params['b3'],
conv_param_3['stride'], conv_param_3['pad']))
self.layers.append(layers.Convolution(self.params['W4'], self.params['b4'],
conv_param_4['stride'], conv_param_4['pad']))
self.layers.append(layers.Convolution(self.params['W5'], self.params['b5'],
conv_param_5['stride'], conv_param_5['pad']))
self.layers.append(layers.Pooling(pool_h=3, pool_w=3, stride=2))
self.layers.append(layers.Dropout(0.5))
self.layers.append(layers.Affine(self.params['W6'], self.params['b6']))
self.layers.append(layers.Relu())
self.layers.append(layers.Dropout(0.5))
self.layers.append(layers.Affine(self.params['W7'], self.params['b7']))
self.layers.append(layers.Relu())
self.layers.append(layers.Affine(self.params['W8'], self.params['b8']))
self.last_layer = layers.SoftmaxWithLoss()
def predict(self, x, train_flg=False):
for layer in self.layers:
if isinstance(layer, layers.Dropout):
x = layer.forward(x, train_flg)
else:
x = layer.forward(x)
return x
def loss(self, x, d):
y = self.predict(x, train_flg=True)
return self.last_layer.forward(y, d)
def accuracy(self, x, d, batch_size=100):
if d.ndim != 1 : d = np.argmax(d, axis=1)
acc = 0.0
for i in range(int(x.shape[0] / batch_size)):
tx = x[i*batch_size:(i+1)*batch_size]
td = d[i*batch_size:(i+1)*batch_size]
y = self.predict(tx, train_flg=False)
y = np.argmax(y, axis=1)
acc += np.sum(y == td)
return acc / x.shape[0]
def gradient(self, x, d):
# forward
self.loss(x, d)
# backward
dout = 1
dout = self.last_layer.backward(dout)
tmp_layers = self.layers.copy()
tmp_layers.reverse()
for layer in tmp_layers:
dout = layer.backward(dout)
# 設定
grads = {}
for i, layer_idx in enumerate((0, 3, 6, 7, 8, 11, 14, 16)):
grads['W' + str(i+1)] = self.layers[layer_idx].dW
grads['b' + str(i+1)] = self.layers[layer_idx].db
return grads
from common import optimizer
import cv2
(x_train, d_train), (x_test, d_test) = load_mnist(flatten=False)
# 処理に時間のかかる場合はデータを削減
x_train, d_train = x_train[::50], d_train[::50]
x_test, d_test = x_test[::20], d_test[::20]
x_train_resize = np.zeros((len(x_train), 1, 224, 224))
for i in range(len(x_train)):
x_train_resize[i][0] = cv2.resize(x_train[i][0], dsize=(224,224))
x_test_resize = np.zeros((len(x_test), 1, 224, 224))
for i in range(len(x_test)):
x_test_resize[i][0] = cv2.resize(x_test[i][0], dsize=(224,224))
print("データ読み込み完了")
network = AlexNet()
optimizer = optimizer.Adam()
iters_num = 600
train_size = x_train.shape[0]
batch_size = 50
train_loss_list = []
accuracies_train = []
accuracies_test = []
plot_interval=10
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train_resize[batch_mask]
d_batch = d_train[batch_mask]
grad = network.gradient(x_batch, d_batch)
optimizer.update(network.params, grad)
loss = network.loss(x_batch, d_batch)
train_loss_list.append(loss)
if (i+1) % plot_interval == 0:
accr_train = network.accuracy(x_train_resize, d_train)
accr_test = network.accuracy(x_test_resize, d_test)
accuracies_train.append(accr_train)
accuracies_test.append(accr_test)
if (i + 1) % 200 == 0:
print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()