「テキストアナリティクスの基礎と実践」をpythonで読む2 共起とbigramのネットワーク分析(networkx使用)

この内容は金明哲さんの「テキストアナリティクスの基礎と実践」のRでの実装をpythonで書き換えながら読んでいくものです。
提供されているデータは、すでに形態素解析されてある程度集計されたデータとなります。

1章当たりの内容が多いので、説明が不十分であること、参考書通りの解析ができているわけではないことはご了承ください。
詳しくは本を読んでいただければと思います。

networkxを使用していますが、不慣れなためコードが見づらい思います。
networkxによるネットワーク分析については補足として記事を投稿しました。
初めて勉強しましたが面白いなと感じました。

画像処理でも記事を投稿していますが、画像や言語系ではとりあえずAI(主にディープラーニング)で分類モデル作成などをやりたくなりますが、こういった分析も必要であると感じました。(これこそ古い考えかもしれませんが)

前回

テキストの基本統計と視覚化

2 共起とbigramのネットワーク分析

2.1 共起とは

要素が文の中で同時に出現(共起)する頻度や組み合わせを分析する主な手法の説明を行う。

形態素の共起

例文

文章の構成要素が文の中で同時に用いられている情報を分析する。

を形態素解析したものを以下に示す。

import MeCab
import re
import numpy as np

mecab = MeCab.Tagger()

texts = [re.split('[\t|,]', x) for x in mecab.parse('文章の構成要素が文の中で同時に用いられている情報を分析する。').split('\n')]
texts[:-2]

[['文章', '名詞', '一般', '*', '*', '*', '*', '文章', 'ブンショウ', 'ブンショー'],
 ['の', '助詞', '連体化', '*', '*', '*', '*', 'の', 'ノ', 'ノ'],
 ['構成', '名詞', 'サ変接続', '*', '*', '*', '*', '構成', 'コウセイ', 'コーセイ'],
 ['要素', '名詞', '一般', '*', '*', '*', '*', '要素', 'ヨウソ', 'ヨーソ'],
 ['が', '助詞', '格助詞', '一般', '*', '*', '*', 'が', 'ガ', 'ガ'],
 ['文', '名詞', '一般', '*', '*', '*', '*', '文', 'ブン', 'ブン'],
 ['の', '助詞', '連体化', '*', '*', '*', '*', 'の', 'ノ', 'ノ'],
 ['中', '名詞', '非自立', '副詞可能', '*', '*', '*', '中', 'ナカ', 'ナカ'],
 ['で', '助詞', '格助詞', '一般', '*', '*', '*', 'で', 'デ', 'デ'],
 ['同時に', '副詞', '一般', '*', '*', '*', '*', '同時に', 'ドウジニ', 'ドージニ'],
 ['用い', '動詞', '自立', '*', '*', '一段', '未然形', '用いる', 'モチイ', 'モチイ'],
 ['られ', '動詞', '接尾', '*', '*', '一段', '連用形', 'られる', 'ラレ', 'ラレ'],
 ['て', '助詞', '接続助詞', '*', '*', '*', '*', 'て', 'テ', 'テ'],
 ['いる', '動詞', '非自立', '*', '*', '一段', '基本形', 'いる', 'イル', 'イル'],
 ['情報', '名詞', '一般', '*', '*', '*', '*', '情報', 'ジョウホウ', 'ジョーホー'],
 ['を', '助詞', '格助詞', '一般', '*', '*', '*', 'を', 'ヲ', 'ヲ'],
 ['分析', '名詞', 'サ変接続', '*', '*', '*', '*', '分析', 'ブンセキ', 'ブンセキ'],
 ['する', '動詞', '自立', '*', '*', 'サ変・スル', '基本形', 'する', 'スル', 'スル'],
 ['。', '記号', '句点', '*', '*', '*', '*', '。', '。', '。']]

この文における名詞は次のようになる。

target_texts = [t[0] for t in texts[:-2] if (t[1] == '名詞')&(t[2] in ['一般', 'サ変接続'])]
target_texts

['文章', '構成', '要素', '文', '情報', '分析']

この文において用いられた「名詞」を集計したものを示す。
表の数値は共起した回数を示す。

import pandas as pd

d1 = pd.read_csv('co_occur.csv', encoding='shift-jis')
d1

	語1	語2	Freq
0	文章	構成	1
1	文章	要素	1
2	文章	文	1
3	文章	情報	1
4	文章	分析	1
5	構成	要素	1
6	構成	文	1
7	構成	情報	1
8	構成	分析	1
9	要素	文	1
10	要素	情報	1
11	要素	分析	1
12	文	情報	1
13	文	分析	1
14	情報	分析	1

bigramは、隣接する要素間の共起である。
今回の例のbigramを示す。
集計の対象外とした語はすべて無視して、集計した語と語の隣接を問題としている。

d1.loc[[0,5,9,12,14]]

	語1	語2	Freq
0	文章	構成	1
5	構成	要素	1
9	要素	文	1
12	文	情報	1
14	情報	分析	1

形態素タグのn-gram

コーパスに基づいた言語学や計量文体学では、形態素タグで集計し、そのunigramやbigramを分析することがある。
例文の形態素タグのbigramの集計結果を示す。

d2 = pd.read_csv('pos.csv', encoding='shift-jis')
d2

	形態素1	形態素2	共起
0	普通名詞	接続助詞	2
1	普通名詞	格助詞	2
2	サ変名詞	動詞	1
3	サ変名詞	普通名詞	1
4	副詞	動詞	1
5	副詞的名詞	格助詞	1
6	動詞	動詞性接尾辞	1
7	動詞	句点	1
8	動詞性接尾辞	動詞性接尾辞	1
9	動詞性接尾辞	普通名詞	1
10	接続助詞	サ変名詞	1
11	接続助詞	副詞的名詞	1
12	格助詞	サ変名詞	1
13	格助詞	副詞	1
14	格助詞	普通名詞	1

2.2 共起の視覚化

ネットワークグラフ

共起データを視覚化する方法として、ネットワークグラフが多く用いられる。
ネットワークグラフとは、構成要素を点とし、共起関係がある点と点を線で連結するグラフである。
矢印のついた有向グラフと矢印のない無向グラフがある。
構成要素を示す点をノード、または頂点と呼び、ノードの多さはネットワークのサイズを表す。
点と点を連結した線を辺、またはエッジと呼び、辺の多さはネットワークの複雑さを表す。

ネットワークの可視化部分は関数化しておく。

styles = {'node_size':2000,
          'font_size':15,
          'node_color':'lightblue',
          'with_labels':True,
          'font_weight':'bold',
          'font_family':'MS Gothic'}

def make_graph(G, nodes, edges, pos, styles=styles, label=True):
    # nodeデータの追加
    G.add_nodes_from(nodes)
 
    # edgeデータの追加
    G.add_weighted_edges_from(edges)
    edge_labels = {(i, j): w['weight'] for i, j, w in G.edges(data=True)}
   
    if not isinstance(pos, dict):
        pos = pos(G)
    
    # ネットワークの可視化
    nx.draw(G, pos=pos, **styles)
    if label:
        nx.draw_networkx_edge_labels(G1, pos=pos, edge_labels=edge_labels) #エッジのラベルを描画

import networkx as nx
import matplotlib.pyplot as plt
import japanize_matplotlib

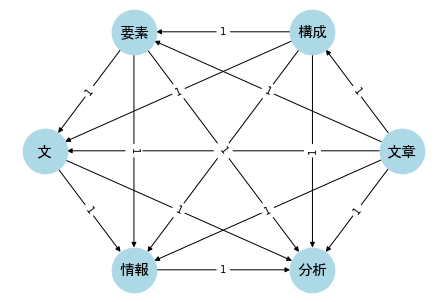
G1 = nx.DiGraph()
nodes1 = target_texts
edges1 = [(d1.loc[i, '語1'], d1.loc[i, '語2'], d1.loc[i, 'Freq']) for i in range(len(d1))]

make_graph(G1, nodes1, edges1, pos=nx.circular_layout)

ネットワークの統計量

基本要素の数と次数

ネットワークにおける基本要素はノードとエッジである。
各ノードにかかるエッジの数を次数と呼ぶ。

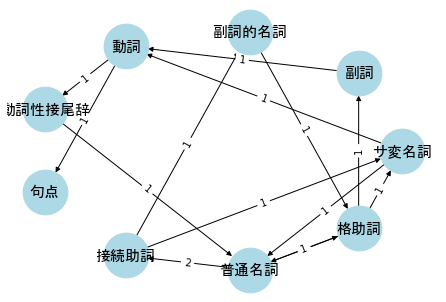
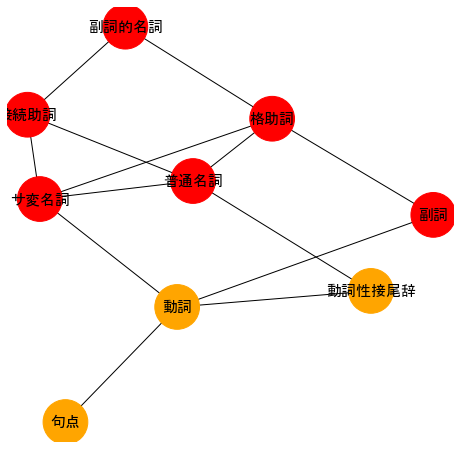
G2 = nx.DiGraph()
nodes2 = np.unique([d2.形態素1]+[d2.形態素2])
edges2 = [(d2.loc[i, '形態素1'], d2.loc[i, '形態素2'], d2.loc[i, '共起']) for i in range(len(d2))]

make_graph(G2, nodes2, edges2, pos=nx.circular_layout)

例えば、「動詞」には4本のエッジがつながっているので、ノード「動詞」の次数は4である。

nx.degree(G2)

DiDegreeView({'サ変名詞': 4, '副詞': 2, '副詞的名詞': 2, '動詞': 4, '動詞性接尾辞': 4, '句点': 1, '接続助詞': 3, '普通名詞': 5, '格助詞': 5})

密度

密度は、ネットワークの混み具合を表す度合いであり、
有向グラフでは$density=m/(n-1)$、無向グラフでは$density=2m/(n-1)$で定義されている。
$n$はノード数、$m$はエッジ数である。

nx.density(G2)

0.20833333333333334

中心性

中心性とは、あるノードのネットワーク内における中心度のことである。
どの指標で中心度を測るかによって、次数中心性、近接中心性、固有ベクトル中心性、媒介中心性などがある。
次数中心性では、他のノードとの間にエッジを多く持つノードほど、中心性が高いことになる。
近接中心性はグラフ上の、あるノードと他のノードの近さに関する指標であり、次の式で定義される。

C(i)=\frac{1}{\sum_{all\ i,j}^{i\neq j}d(n_i,n_j)}

$d(n_i,n_j)$は、ノード$n_i$とノード$n_j$の最短距離である。
近接中心性は値が高いほど中心性が高い。
しかし、ネットワークのノード数が異なるとお互いに比較することができないため、次のように標準化した式を用いる。

C'(i)=\frac{n-1}{\sum_{all\ i,j}^{i\neq j}d(n_i,n_j)}

媒介中心性は、あるノードを通過しないと他のノードに到達できない度合いである。
あるノードが、それ以外の2つのノードを結ぶ最短経路上にあるかどうかについての指標であり、値が大きいほど中心性が高い。
固有ベクトル中心性は、隣接行列の第1固有ベクトルを用いて、隣接するノードの中心性を表す指標である。
次数の多さよりも、中心性の高いノードと接続していることに注目するものであり、値が大きいほど中心性が高い。

# 次数中心性
degree_centers = nx.degree_centrality(G1)
sorted(degree_centers.items(), key=lambda x: x[1], reverse=True)[:5]

[('文章', 1.0), ('構成', 1.0), ('要素', 1.0), ('文', 1.0), ('情報', 1.0)]

# 近接中心性
close_centers = nx.closeness_centrality(G1)
sorted(close_centers.items(), key=lambda x: x[1], reverse=True)[:5]

[('分析', 1.0), ('情報', 0.8), ('文', 0.6), ('要素', 0.4), ('構成', 0.2)]

# 媒介中心性
between_centers = nx.betweenness_centrality(G1)
sorted(between_centers.items(), key=lambda x: x[1], reverse=True)[:5]

[('文章', 0.0), ('構成', 0.0), ('要素', 0.0), ('文', 0.0), ('情報', 0.0)]

クラスターの係数

クラスターの係数はノードの近傍の関係を示す度合いであり、あるノードに隣接するノード同士の間につながりがあるかどうか、
つまり、三角形ループが形成されているかどうかについての指標である。
推移性ともよばれ、グローバルクラスター係数やローカルクラスター係数などに細分化できる。
グローバルクラスター係数は、すべてのノードのクラスター係数の平均値のことである。
ローカルクラスター係数は、個別のノードのクラスター係数のことである。
グローバルクラスター係数は、次の式で定義される。
$B$は、隣接行列$A$の内積の主対角成分をゼロにした行列である。

B_{transitivity}=\frac{\sum(B×A)}{\sum(B)}=\frac{3×三角形の数}{2つのエッジを持つノード数}

ローカルクラスター係数は、次の式で定義される。
式の中の$v_i$はノード、$k_i$はノード$v_i$の次数を示す。

L_{transitivity}=\frac{2×v_iを含む三角形の数}{k_i(k_i-1)}

クラスター係数が大きいほど、ネットワークグラフ全体が1つにまとまる。

パスとその長さ

パスはノードの間をつなぐルートのことを指す。
つまり、ノード$v_i$からノード$v_k$にたどり着くために通るエッジの数である。
平均パスが短く、クラスター係数が高いネットワークをスモールワールドネットワークと呼ぶ。

コミュニティ分析

1つのネットワークをいくつかのサブネットワークに分けたものをコミュニティと呼ぶ。
コミュニティの抽出は、オーバーラッピングを考えない方法とオーバーラッピングを考える方法に大別される。
ここでのオーバーラッピングとは、あるノードが複数のコミュニティに属することを示す。

# Graphオブジェクトの作成
G3 = nx.Graph()
 
# nodeデータの追加
com1 = ["a", "b", "c", "d"]
com2 = ["1", "2", "3", "4", "5"]
nodes3 = com1 + com2

edges3 = []
for i in range(len(com1)):
    for j in range(len(com1[i:])):
        edges3 += [(com1[i], com1[i+j], 1)]

for i in range(len(com2)):
    for j in range(len(com2[i:])):
        edges3 += [(com2[i], com2[i+j], 1)]
edges3+= [("2", "d", 1)]

pos = {}
n1=len(com1)
for i in np.arange(n1):
    pos.update({com1[i]: (0.5+0.3*np.sin(2*np.pi/n1*i), 0.8*np.cos(2*np.pi/n1*i))})

n2=len(com2)
for i in np.arange(n2):
    pos.update({com2[i]: (-0.5+0.3*np.sin(2*np.pi/n2*i), 0.8*np.cos(2*np.pi/n2*i))})

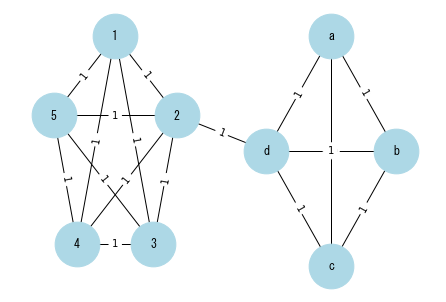
make_graph(G3, nodes3, edges3, pos=pos)
plt.xlim(-1,1)
plt.ylim(-1,1)

コミュニティ分析はネットワークを何らかの特徴によりいくつかのサブネットワークに分割して、分析を行う方法である。
コミュニティのクラスタリングは、次の$Q$値が最大になるような分割を行う方法が多く用いられている。
$A_{ij}$は隣接行列の要素、$M$はエッジの総数、$k_i$はノード$i$の次数、
$\delta(c_i,c_j)$はノード$i$とノード$j$が同じクラスターに属する場合は1を、そうでない場合には0をとる。

Q=\frac{1}{2M}\sum\biggl(A_{ij}-\frac{k_ik_j}{2M}\delta(c_i,c_j) \biggr)

何らかの制約条件の下で計算を行うアルゴリズムとしては、焼き増し法、ランダム・ウォーク法、全探索法などがある。
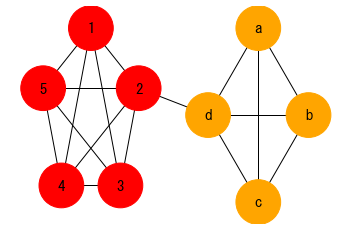
コミュニティ分割の例を示す。

from networkx.algorithms.community import greedy_modularity_communities

colors = ['red', 'orange', 'yellow', 'green', 'lightgreen', 'royalblue', 'blue', 'violet']
lst_m = greedy_modularity_communities(G3)
color_map_m = ['black'] * nx.number_of_nodes(G3)
counter = 0
for c in lst_m:
    for n in c:
        color_map_m[nodes3.index(n)] = colors[counter]
    counter = counter + 1

nx.draw_networkx_edges(G3, pos);
nx.draw_networkx_nodes(G3, pos, node_size=2000, node_color=color_map_m);
nx.draw_networkx_labels(G3, pos=pos, font_size=15, font_family='MS Gothic');
plt.xlim(-1,1)
plt.ylim(-1,1)
plt.axis('off')

from networkx.algorithms.community import greedy_modularity_communities

g2 = nx.Graph(G2)

colors = ['red', 'orange', 'yellow', 'green', 'lightgreen', 'royalblue', 'blue', 'violet']
lst_m = greedy_modularity_communities(g2)
color_map_m = ['black'] * nx.number_of_nodes(g2)
counter = 0
for c in lst_m:
    for n in c:
        color_map_m[nodes2.index(n)] = colors[counter]
    counter = counter + 1

pos = nx.spring_layout(g2, k=0.25,iterations=30)

plt.figure(figsize=(8,8))
nx.draw_networkx_edges(g2, pos);
nx.draw_networkx_nodes(g2, pos, node_size=2000, node_color=color_map_m);
nx.draw_networkx_labels(g2, pos=pos, font_size=15, font_family='MS Gothic');
plt.axis('off')

2.3 ネットワーク分析例

データの俯瞰

d3 = pd.read_csv('anketo.csv', encoding='shift-jis')
d3.head()

	Term1	Term2	度数
0	学費を	低く/安く	20
1	単位を	取り	4
2	もっと	取り	3
3	自動車通学の	許可。	3
4	学食を	安く。	3

styles = {'node_size':10,
          'font_size':15,
          'node_color':'lightblue',
          'with_labels':False,
          'font_weight':'bold',
          'width':0.2,
          'font_family':'MS Gothic'}

G4 = nx.DiGraph()
nodes4 = np.unique([d3.Term1]+[d3.Term2])
edges4 = [(d3.loc[i, 'Term1'], d3.loc[i, 'Term2'], d3.loc[i, '度数']) for i in range(len(d3))]

make_graph(G4, nodes4, edges4, pos=nx.spring_layout, styles=styles, label=False)

基本統計量を用いた探索的分析

次数を求め、その大きい順に上位5つを示す。

sorted(dict(G4.degree).items(), key=lambda x:x[1], reverse=True)[:5]

[('もっと', 39), ('して欲しい。', 14), ('無い。', 10), ('やって欲しい。', 9), ('分かり', 8)]

np.argsort(list(dict(G4.degree).values()))[::-1][:5]

array([134,  63, 677, 140, 319], dtype=int64)

「もっと」がもっとも次数が高い。
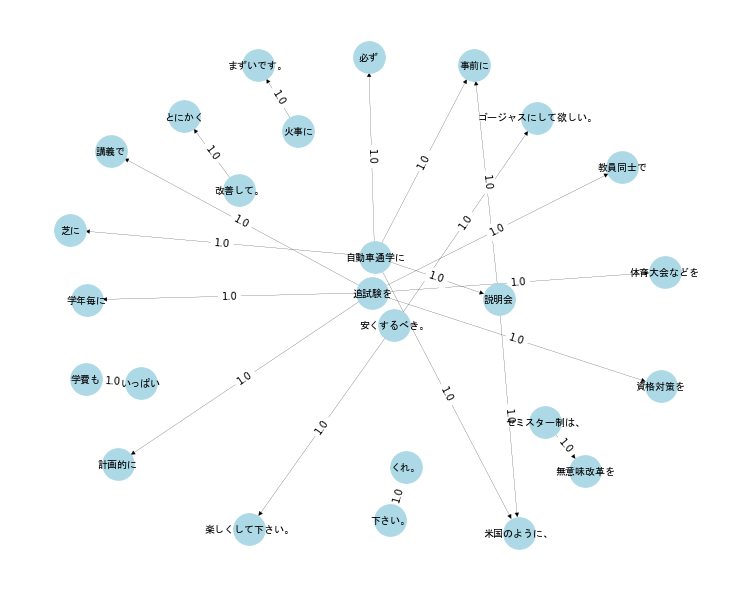
「もっと」とパス1の長さでリンクされているノードを抽出し、作成したネットワークを示す。

styles = {'node_size':1000,
          'font_size':15,
          'node_color':'lightblue',
          'with_labels':True,
          'font_weight':'bold',
          'font_family':'MS Gothic'}

G5 = nx.DiGraph()

# nodeデータの追加
nodes5 = ['もっと']+list([d3.Term2[d3.Term1=='もっと']][0])
edges5 = [(d3.loc[i, 'Term1'], d3.loc[i, 'Term2'], d3.loc[i, '度数']) for i in range(len(d3)) if d3.loc[i, 'Term1'] == 'もっと']

plt.figure(figsize=(12,12))
make_graph(G5, nodes5, edges5, pos=nx.spring_layout, styles=styles, label=True)

次に、「学費を」でからパス4までのノードをプロットした結果を示す。

g = nx.Graph()
g.add_nodes_from(nodes4)
g.add_edges_from([(d3.loc[i, 'Term1'], d3.loc[i, 'Term2']) for i in range(len(d3))])
targets = list(nx.single_target_shortest_path(g, "学費を", cutoff=4).keys())
g.add_edges_from([(d3.loc[i, 'Term1'], d3.loc[i, 'Term2']) for i in range(len(d3))])
targets3 = list(nx.single_target_shortest_path(g, "学費を", cutoff=3).keys())

styles = {'node_size':1000,
          'font_size':10,
          'node_color':'lightblue',
          'with_labels':True,
          'font_weight':'bold',
          'font_family':'MS Gothic'}

G6 = nx.DiGraph()
 
# nodeデータの追加
nodes6 = targets
edges6 = [(d3.loc[i, 'Term1'], d3.loc[i, 'Term2'], d3.loc[i, '度数'])
             for i in range(len(d3)) if (d3.loc[i, 'Term1'] in targets3)|(d3.loc[i, 'Term2'] in targets3)]

# 色の設定
color_map = []
for node in nodes6:
    if node == '学費を':
        color_map.append('lightgreen')
    else:
        color_map.append('lightblue')

styles['node_color'] = color_map

pos = lambda x: nx.spring_layout(x, pos=nx.spectral_layout(x, scale=0.25), k=0.25,iterations=30)
    

plt.figure(figsize=(12,8))
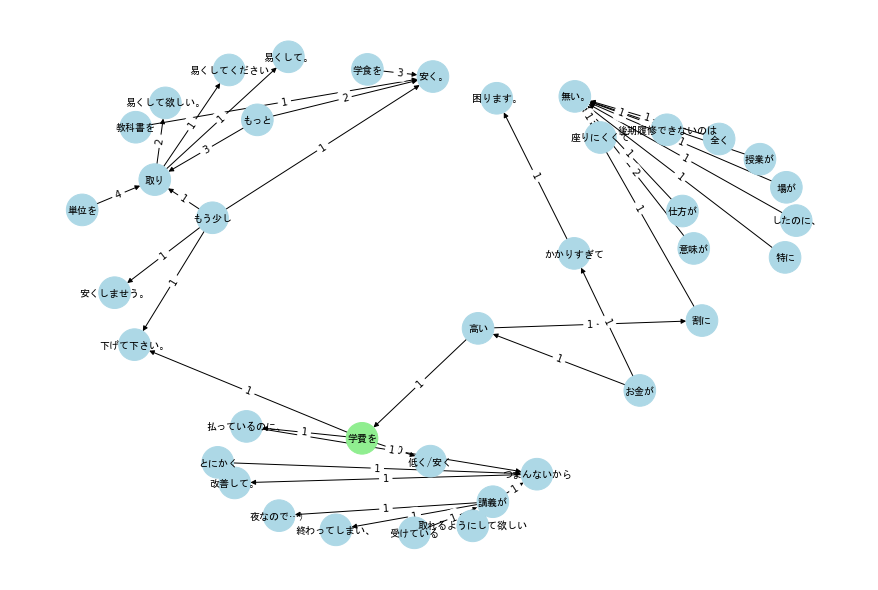
make_graph(G6, nodes6, edges6, pos=pos, styles=styles, label=True)

ここでは、エッジの太さを共起頻度に比例させたグラフを示しているが、「学費を→低く/安く」が太く目立っている。
これは、アンケート結果では、学費に不満があることを物語っている。

コミュニティの考察

ここでは、ガーバンニューマンのアルゴリズムを利用したコミュニティ分析の例を示す。

from networkx.algorithms import community
import itertools

k = 3

comp = community.girvan_newman(G6)

community_list = []
for communities in itertools.islice(comp, k-1):
    community_list.append(tuple(sorted(c) for c in communities))
community_list = list(community_list[k-2])

color_map = []

for node in nodes6:
    if node == '学費を':
        color_map.append('lightgreen')
    elif node in community_list[0]:
        color_map.append('silver')
    elif node in community_list[1]:
        color_map.append('yellow')
    else:
        color_map.append('skyblue')

styles['node_color'] = color_map
plt.figure(figsize=(12,8))
make_graph(G6, nodes6, edges6, pos=pos, styles=styles, label=True)

2.4 共起の強さの係数

共起関係の強さは、共起頻度にある程度反映される。
ただし、頻度が高いからと言って必ずしも共起関係が強いとは限らない。
共起データのペアを分割表にしたものの一般形を示す。

			Y
		1	0	合計
X	1	$$a=f_{11}$$	$$b=f_{12}$$	$$a+b=f_{1+}$$
	0	$$c=f_{21}$$	$$d=f_{22}$$	$$c+d=f_{2+}$$
	合計	$$a+c=f_{+1}$$	$$b+d=f_{+2}$$	$$N=a+b+c+d$$

言語データにおける共起データでは、一般的に$d=f_{22}$の値が突出する場合が多く、全体のファイ係数に影響を与えている。
このようなこともあり、$X$、$Y$関係に関する測度が多数提案されている。
2つの項目の共起の強さを計測する分野では、連関測度とも呼ぶ。
日本では、Jaccard係数が多く用いられている。

語$x$と$y$の共起の確率は$p(x,y)=p(x)p(y|x)$、$p(x,y)=p(y)p(x|y)$で求めることができる。
この両式が成り立つ確率は次式となる。

p(y|x)p(x|y)=\frac{p(x,y)^2}{p(x)p(y)}

これを表の表記で示すと$a^2/(a+b)(c+d)$となる。
これを同時条件付き確率と呼ぶことにする。これはOchiai測度の2乗に等しい。

G = nx.Graph()
G.add_nodes_from(nodes4)
G.add_weighted_edges_from(edges4)

j_coef = [(a,b,c) for a,b,c in nx.jaccard_coefficient(G) if c != 0]
j_20 = sorted(j_coef, key=lambda x: x[2], reverse=True)[:20]

styles = {'node_size':1000,
          'font_size':10,
          'node_color':'lightblue',
          'with_labels':True,
          'font_weight':'bold',
          'font_family':'MS Gothic',
          'width':0.2}

G7 = nx.DiGraph()

# nodeデータの追加
nodes7 = np.unique(np.array(j_20)[:,0:2].ravel())
edges7 = j_20

pos = lambda x: nx.spring_layout(x, k=0.6,iterations=100)

plt.figure(figsize=(10,8))
make_graph(G7, nodes7, edges7, pos=pos, styles=styles, label=True)

以上となります。

次回

テキストの特徴分析

参考書