LoginSignup
3
5

More than 1 year has passed since last update.

@tanaka_benkyo

pythonで「異常検知と変化検知」を読む7 ガウス過程回帰による異常検知

Last updated at Posted at 2022-12-16

「異常検知と変化検知」は異常検知の本です。アルゴリズム部分をpythonで実装していきたいと思います。たくさんの方が同じ内容をより良い記事でとして投稿しています。

個人的な勉強のメモ書きとなります。
私には難しい内容であり、コードがかなり汚いです。申し訳ありません。
まとめることが目的ではないので本文について参考書とほぼ同じ表現となっています。問題があればお教えください。
興味を持ったり、導出や詳細などを知りたい方は「異常検知と変化検知」を読んでいただければと思います。

参考

前回

方向データの異常検知

ガウス過程回帰による異常検知

入出力がある場合の異常検知の考え方

$D={(\boldsymbol{x}^{(1)},y^{(1)}),\cdots,(\boldsymbol{x}^{(N)},y^{(N)})}$ のような入力と出力の対からなるデータを考える。
$y$はスカラー、入力$\boldsymbol{x}$は$M$次元とする。
与えられた入力に対して出力を眺めて、それが通常の振る舞いにより期待される値から大幅にすれているかを見るという意味で、応答異常検知問題と呼ぶこともある。
入力に対する出力の関数$f$と、観測の際含まれるであろうノイズの双方をデータから学習しなければならない。
これを、回帰ないし回帰問題と呼ぶ。また、関数$f(\boldsymbol{x})$を応答曲面と呼ぶ。

ガウス過程の観測モデルと事前分布

任意の座標$\boldsymbol{x}$における応答曲面の出力を$f(\boldsymbol{x})$とする。
ガウス過程回帰のモデルは次の2つの要素からなる。

  • 観測時のノイズを表す確率モデル
  • 応答曲面の滑らかさを表現する事前分布
観測モデル

観測時のノイズを表すモデルは、次のように正規分布として仮定する。
$$
p(y|\boldsymbol{x},\sigma^2)=\mathcal{N}(y|f(\boldsymbol{x}),\sigma^2)
$$

入力$\boldsymbol{x}$における応答曲面の値$f(\boldsymbol{x})$の分布が、データ$D$から$p(f(\boldsymbol{x})|D)$のように得られていれば、
$$
p(y|\boldsymbol{x},D,\sigma^2)=\int_{-\infty}^{\infty}df\mathcal{N}(y|f(\boldsymbol{x}),\sigma^2)p(f(\boldsymbol{x})|D)
$$
のように解を得ることができる。この分布は、予測分布と呼ばれる。

応答曲面の滑らかさを制御するモデル

$N$個の入力
$$
\boldsymbol{f}_N=(f(\boldsymbol{x}^{(1)}),\cdots,f(\boldsymbol{x}^{(N)}))^T
$$
があった場合、$\boldsymbol{f}_N$は、
$$
p(\boldsymbol{f}_N)=\mathcal{N}(\boldsymbol{f}_N|\boldsymbol{0},K)
$$
のような事前分布に従う、というのがガウス過程の基本的な想定である。
ただし、$K$はその$(i,j)$成分が$K(\boldsymbol{x}^{(i)},\boldsymbol{x}^{(j)})$で与えられるような行列である。

ガウス過程回帰の問題設定

予測分布に至るまでの順番は次の通りになる。

  • データ$D$をもとに、$\boldsymbol{f}_N$の分布$p(\boldsymbol{f}_N|D)$を求める
  • $p(\boldsymbol{f}_N|D)$と、応答曲面に関する滑らかさについての事前分布から、任意の$\boldsymbol{x}$に対する応答曲面の値$f(\boldsymbol{x})$の確率分布$p(f(\boldsymbol{x})|D)$を求める
  • $$p(y|\boldsymbol{x},D,\sigma^2)=\int_{-\infty}^{\infty}df\mathcal{N}(y|f(\boldsymbol{x}),\sigma^2)p(f(\boldsymbol{x})|D)
    $$
    を使って予測分布を得る

応答曲面の事後分布

データ$D$をもとに、$\boldsymbol{f}_N$の分布$p(\boldsymbol{f}_N|D)$を求める。
ベイズの定理を使うと次のようになる。
$$
p(\boldsymbol{f}_N|D)=\frac{p(D|\boldsymbol{f}_N,\sigma^2)p(\boldsymbol{f}_N)}{\int d\boldsymbol{f}'_N p(D|\boldsymbol{f}'_N,\sigma^2)p(\boldsymbol{f}'_N)}
$$

計算を進めると(計算は省略)、

$$
p(\boldsymbol{f}_N|D)=\mathcal{N}\bigg(\boldsymbol{f}_N|\frac{1}{\sigma^2}M\boldsymbol{y}_N,M \bigg)
$$
が得られる。ここで、
$$
M=\sigma^2K(K+\sigma^2\boldsymbol{I}_N)^{-1}
$$
である。

予測分布の導出

応答曲面の値$f(\boldsymbol{x})$の確率分布$p(f(\boldsymbol{x})|D)$は、
$$
p(f(\boldsymbol{x})|D)=\int d\boldsymbol{f}_Np(f(\boldsymbol{x})|\boldsymbol{f}_N)p(\boldsymbol{f}_N|D)
$$
と書ける。
ここで、$f(\boldsymbol{x})$と$\boldsymbol{f}_N$の同時分布は
$$
p\begin{pmatrix}f(\boldsymbol{x})\ \boldsymbol{f}_N \end{pmatrix} = \mathcal{N}\bigg(\boldsymbol{0},\begin{bmatrix}K_0&\boldsymbol{k}^T\ \boldsymbol{k}&K \end{bmatrix} \bigg)
$$
と書き下すことができる。ただし$\boldsymbol{k}=(K(\boldsymbol{x},\boldsymbol{x}^{(1)}),\cdots,K(\boldsymbol{x},\boldsymbol{x}^{(N)}))^T$および$K_0=K(\boldsymbol{x},\boldsymbol{x})$と定義した。
$$
p(f(\boldsymbol{x})|\boldsymbol{f}_N)=\mathcal{N}(f(\boldsymbol{x}|\boldsymbol{k}^TK^{-1}\boldsymbol{f}_N,K_0-\boldsymbol{k}^TK^{-1}\boldsymbol{k}))
$$
となることから、$\boldsymbol{f}_N$を積分消去することで、

p(f(\boldsymbol{x})|D)=\mathcal{N}(\mu_f(\boldsymbol{x}),\sigma^2_f(\boldsymbol{x}))\\
\mu_f(\boldsymbol{x})=\boldsymbol{k}^T(K+\sigma^2\boldsymbol{I}_N)^{-1}\boldsymbol{y}_N\\
\sigma^2_f(\boldsymbol{x})=K_0-\boldsymbol{k}^T(K+\sigma^2\boldsymbol{I}_N)^{-1}\boldsymbol{k}

として求めることができる。(計算は省略)

最後に、
$$
p(y|\boldsymbol{x},D,\sigma^2)=\int_{-\infty}^{\infty}df\mathcal{N}(y|f(\boldsymbol{x}),\sigma^2)p(f(\boldsymbol{x})|D)
$$
から、$f(\boldsymbol{x})$を積分消去すると、

p(y|\boldsymbol{x},D,\sigma^2)=\mathcal{N}(y|\mu_y(\boldsymbol{x}),\sigma_y^2(\boldsymbol{x}))\\
\mu_y(\boldsymbol{x})=\boldsymbol{k}^T(K+\sigma^2\boldsymbol{I}_N)^{-1}\boldsymbol{y}_N\\
\sigma_y^2(\boldsymbol{x})=\sigma^2+K_0-\boldsymbol{k}^T(K+\sigma^2\boldsymbol{I}_N)^{-1}\boldsymbol{k}

となることが示せる。

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal
from scipy.stats import norm

# カーネル関数(RBFカーネル)を定義
def RBF_kernel(xi, xj, gamma, l):
    return gamma * np.exp(-(xi-xj.T)*(xi-xj.T) / (l**2))

# データの準備(実際の値)
x_act = np.arange(-np.pi, np.pi, 0.01).reshape(-1,1)
y_act = (np.sin(x_act*5)+np.sin(x_act*2)+0.2*x_act).reshape(-1,1)

plt.plot(x_act, y_act)

image.png

# ランダムで10点選ぶ
idx = np.sort(np.random.randint(len(x_act), size=10))

# データをサンプリング
xi = x_act[idx]
yi = y_act[idx]

# カーネル
K = RBF_kernel(xi, xi, gamma=1, l=1)

# サンプル数、分散
N = len(xi)
sigma2 = 1

# 分散行列Mと平均値μの計算
M = sigma2*K@np.linalg.inv(K+sigma2*np.eye(N))
mu_hat = 1/sigma2 * M @ yi

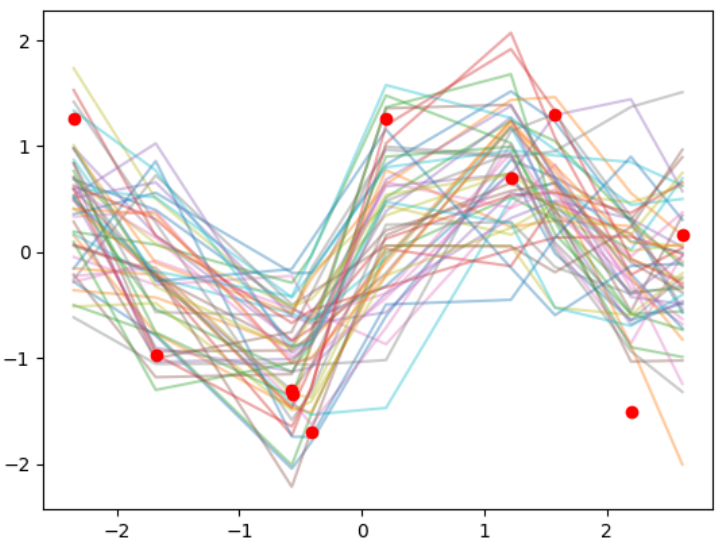
# 予測分布からサンプリングを行う
for i in range(50):
    f_pred = multivariate_normal.rvs(mean=mu_hat.ravel(), cov=M)
    plt.plot(xi, f_pred, alpha=.4)

# 観測値のプロット
plt.plot(xi, yi, 'o', c='r')

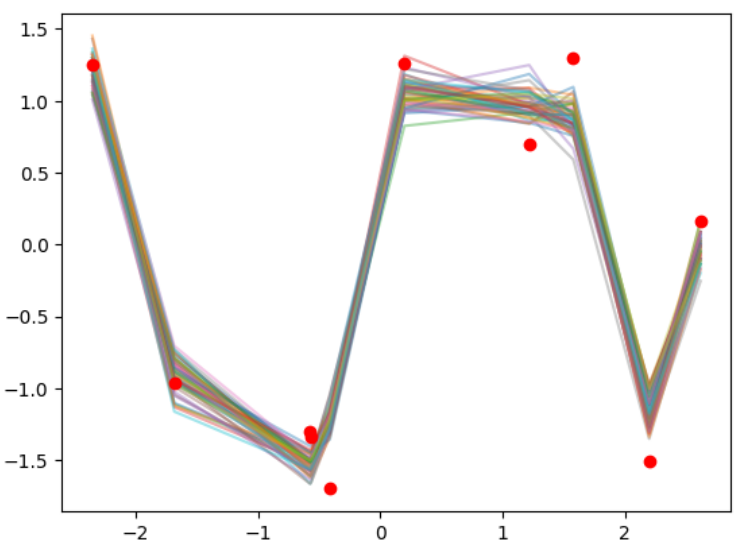
image.png

# 分散を小さくする
sigma2 = 0.01

# 分散行列Mと平均値μの計算
M = sigma2*K@np.linalg.inv(K+sigma2*np.eye(N))
mu_hat = 1/sigma2 * M @ yi

# 予測分布からサンプリングを行う
for i in range(50):
    f_pred = multivariate_normal.rvs(mean=mu_hat.ravel(), cov=M)
    plt.plot(xi, f_pred, alpha=.4)

# 観測値のプロット
plt.plot(xi, yi, 'o', c='r')

image.png

予測分布の導出を行う。

# 各カーネル行列の計算
gamma = 10
l = 1

K  = RBF_kernel(xi, xi, gamma=gamma, l=l)
K0 = RBF_kernel(x_act, x_act, gamma=gamma, l=l)
k  = RBF_kernel(xi, x_act, gamma=gamma, l=l)

# パラメータの計算
sigma2 = 0.01
muy = k.T@np.linalg.inv(K+sigma2*np.eye(N))@yi
sigmay2 = sigma2 + K0 - k.T@np.linalg.inv(K+sigma2*np.eye(N))@k
sy2 = np.diag(sigmay2)

# 予測分布からサンプリングを行う
for i in range(10):
    y_pred = multivariate_normal.rvs(mean=muy.ravel(), cov=sigmay2)
    plt.plot(x_act, y_pred, alpha=.5)

# 観測値のプロット
plt.plot(xi, yi, 'o', c='r')

# yの予測分布
plt.plot(x_act, muy, linestyle='--', color='red')
plt.fill_between(x_act.ravel(),(muy.ravel()+np.sqrt(sy2)),(muy.ravel()-np.sqrt(sy2)), color='red', alpha=.1)

image.png

異常度の定義とガウス過程の性質

ガウス過程に基づく異常度の定義

異常度の一般的な定義を適用すると、
$$
\begin{align}
a(y',\boldsymbol{x}')&=-\ln p(y'|\boldsymbol{x}',D,\sigma^2)\
&=\frac{1}{2}\ln{2\pi \sigma_y^2(\boldsymbol{x}')}+\frac{1}{2\sigma_y^2(\boldsymbol{x}')}{y'-\mu_y(\boldsymbol{x}')}^2
\end{align}
$$
のように異常度を定義できる。

y = np.arange(-5,5,0.1)

a = 1/2*np.log(2*np.pi*sy2.reshape(-1,1))+1/(2*sy2.reshape(-1,1))*(y-muy)**2
plt.contourf(x_act.ravel(), y, a.T, origin='lower', levels=40, alpha=.4, cmap=plt.cm.Blues)
plt.contour(x_act.ravel(), y, a.T, origin='lower', levels=np.arange(0,100,10), colors='blue')

plt.plot(xi, yi, 'o', c='r')
plt.plot(x_act, muy, linestyle='--', color='red')

image.png

σ2と他のパラメータの決定

周辺化尤度を最大にするように$\sigma^2$を選ぶ。

$$
E(\sigma^2|D)=\int d\boldsymbol{f}_N p(D|\boldsymbol{f}_N,\sigma^2)p(\boldsymbol{f}_N)
$$

$E(\sigma^2|D)$をエビデンスと呼ぶ。エビデンスの最大化によるパラメータ決定法を、第2種最尤推定法や経験ベイズ法と呼ぶ。
ここで計算は省略するが、
$$
E(\sigma^2|D)=\mathcal{N}(\boldsymbol{y}_N|\boldsymbol{0},\sigma^2\boldsymbol{I}_N+K)
$$
と計算できる。
いま、
$$
K=\sigma^2\tilde{K}
$$
のようにカーネル行列から$\sigma^2$をくくりだし、無次元化したカーネル行列$\tilde{K}$を定義したとすると、
$$
\hat{\sigma}^2=\frac{1}{N}\boldsymbol{y}_N^T(\boldsymbol{I}_N+\tilde{K})^{-1}\boldsymbol{y}_N
$$
という推定式が得られる。
たとえばRBFカーネルを使ったとすると、$\tilde{K}$の$(i,j)$成分は

\tilde{K}_{i,j}=\gamma \exp\bigg(-\frac{|\boldsymbol{x}^{(i)}-\boldsymbol{x}^{(j)}|^2}{\mathcal{l}^2} \bigg)

のようになり、係数$\gamma$と、カーネルの到達範囲を表すパラメータ$\mathcal{l}$を決める必要がある。
解を対数エビデンスに入れ戻すと、

\ln E(\gamma, \mathcal{l}|D)=-\frac{N}{2}\bigg\{\ln \bigg(\frac{2\pi}{N} \bigg)+1 \bigg\}-\frac{1}{2}\ln\bigg|\boldsymbol{I}_N+\tilde{K} \bigg|-\frac{N}{2}\ln\{\boldsymbol{y}_N^T(\boldsymbol{I}_N+\tilde{K})^{-1}\boldsymbol{y}_N \}

のように新たにエビデンスを$(\gamma, \mathcal{l})$の関数と考え、対数エビデンスを最大化するようパラメータを決める

アルゴリズム(ガウス過程回帰による異常検知)

  • パラメータの決定
    データ$D={(\boldsymbol{x}^{(1)},y^{(1)}),\cdots,(\boldsymbol{x}^{(N)},y^{(N)})}$を用意する。カーネル関数の形を与える。
    ・(RBFカーネルの場合)$\gamma$の値の候補を1を中心にしていくつか与える。$l$の値の候補を、データ$D$における$\boldsymbol{x}$の広がりを参考にしていくつか与える。
    ・$(\gamma,l)$の組み合わせのそれぞれについて対数エビデンスを計算する。
\ln E(\gamma, \mathcal{l}|D)=-\frac{N}{2}\bigg\{\ln \bigg(\frac{2\pi}{N} \bigg)+1 \bigg\}-\frac{1}{2}\ln\bigg|\boldsymbol{I}_N+\tilde{K} \bigg|-\frac{N}{2}\ln\{\boldsymbol{y}_N^T(\boldsymbol{I}_N+\tilde{K})^{-1}\boldsymbol{y}_N \}

・対数エビデンスを最大にするものを推定値$(\hat{\gamma},\hat{l})$とする
・$(\hat{\gamma},\hat{l})$から$\hat{\sigma}^2$を求める
$$
\hat{\sigma}^2=\frac{1}{N}\boldsymbol{y}_N^T(\boldsymbol{I}_N+\tilde{K})^{-1}\boldsymbol{y}_N
$$

  • 異常度の計算
    事前に$(K+\sigma^2\boldsymbol{I}_N)^{-1}\boldsymbol{y}_N$を計算しておく。
    ・予測分布の平均$\mu_y(\boldsymbol{x}')$と分散$\sigma_y^2(\boldsymbol{x}')$を計算する。
\mu_y(\boldsymbol{x})=\boldsymbol{k}^T(K+\sigma^2\boldsymbol{I}_N)^{-1}\boldsymbol{y}_N\\
\sigma_y^2(\boldsymbol{x})=\sigma^2+K_0-\boldsymbol{k}^T(K+\sigma^2\boldsymbol{I}_N)^{-1}\boldsymbol{k}

・異常度$a(\boldsymbol{x}')$を計算する。

a(\boldsymbol{x}')=\frac{1}{2}\ln\{2\pi \sigma_y^2(\boldsymbol{x}')\}+\frac{1}{2\sigma_y^2(\boldsymbol{x}')}\{y'-\mu_y(\boldsymbol{x}')\}^2
  • 異常判定
    $a(\boldsymbol{x}')$が閾値よりも大きければ警報を出す。
# γとlの候補
gammas = np.array([10,100,1000])
ls=np.arange(0.1,1.5,0.1)

# 対数エビデンスの計算
lnE = np.zeros((len(gammas), len(ls)))
for i, g in enumerate(gammas):
    for j, l in enumerate(ls):
        K = RBF_kernel(xi, xi, gamma=g, l=l)
        lnE[i, j]=-N/2*(np.log(2*np.pi/N)+1)-1/2*np.log(np.linalg.det(np.eye(N)+K))-N/2*np.log(yi.T@np.linalg.inv(np.eye(N)+K)@yi)

# 対数エビデンスを最大にするパラメータ
idx1, idx2 = np.where(lnE==np.max(lnE))
best_g = gammas[idx1]
best_l = ls[idx2]
print(best_g, best_l)

# 各カーネル行列の計算
gamma = best_g
l = best_l

# σ2の計算
K_tilde  = RBF_kernel(xi, xi, gamma=gamma, l=l)
sigma2 = yi.T@np.linalg.inv(np.eye(N)+K_tilde)@yi/N

# カーネル関数の計算
K  = sigma2*RBF_kernel(xi, xi, gamma=gamma, l=l)
K0 = sigma2*RBF_kernel(x_act, x_act, gamma=gamma, l=l)
k  = sigma2*RBF_kernel(xi, x_act, gamma=gamma, l=l)

# 予測分布の平均と分散の計算
muy = k.T@np.linalg.inv(K+sigma2*np.eye(N))@yi
sigmay2 = sigma2 + K0 - k.T@np.linalg.inv(K+sigma2*np.eye(N))@k
sy2 = np.diag(sigmay2)

fig, ax = plt.subplots(2,1,figsize=(8,5))

# 観測値のプロット
ax[0].plot(xi, yi, 'o', c='r')

# yの予測分布
ax[0].plot(x_act, muy, linestyle='--', color='red')
ax[0].fill_between(x_act.ravel(),(muy.ravel()+np.sqrt(sy2)),(muy.ravel()-np.sqrt(sy2)), color='red', alpha=.1)

# 異常度の計算
y = np.arange(-5,5,0.1)
a = 1/2*np.log(2*np.pi*sy2.reshape(-1,1))+1/(2*sy2.reshape(-1,1))*(y-muy)**2

# 異常度のプロット
ax[1].contourf(x_act.ravel(), y, a.T, origin='lower', levels=40, alpha=.4, cmap=plt.cm.Blues)
ax[1].contour(x_act.ravel(), y, a.T, origin='lower', levels=np.arange(0,100,10), colors='blue')

ax[1].plot(xi, yi, 'o', c='r')
ax[1].plot(x_act, muy, linestyle='--', color='red')

image.png

実験計画法への応用

過去の$N$回のシミュレーション結果$D={(\boldsymbol{x}^{(1)},y^{(1)}),\cdots,(\boldsymbol{x}^{(N)},y^{(N)})}$を活用して「次にシミュレーションで調べるべき最適な$\boldsymbol{x}$は何か」という問いに答えたい、というのが問題意識である。
最適性の定義の最も基本的なものは、次の期待改善量である。

J(\boldsymbol{x})=\int_{-\infty}^{\infty}dy p(y|\boldsymbol{x},D,\sigma^2)[y_{min}-y]_{+}

ここで、評価値$y$は小さければ小さいほどよいようなものであると仮定している。
$[・]_{+}$はカッコの中身が正なら何もせず、負なら$0$に置き換える演算を表す。
さらに次のように計算できる。
$$
J(\boldsymbol{x})=\sigma_y(\boldsymbol{x})[z\Phi (z)+\mathcal{N}(z|0,1)]
$$
ただし$\Phi$は標準正規分布の累積分布関数で、

\Phi(v)=\int_{-\infty}^vdu\mathcal{N}(v|0,1)

で定義される。また、$z$は、
$$
z=\frac{y_{min}-\mu_y(\boldsymbol{x})}{\sigma_y(\boldsymbol{x})}
$$

である。

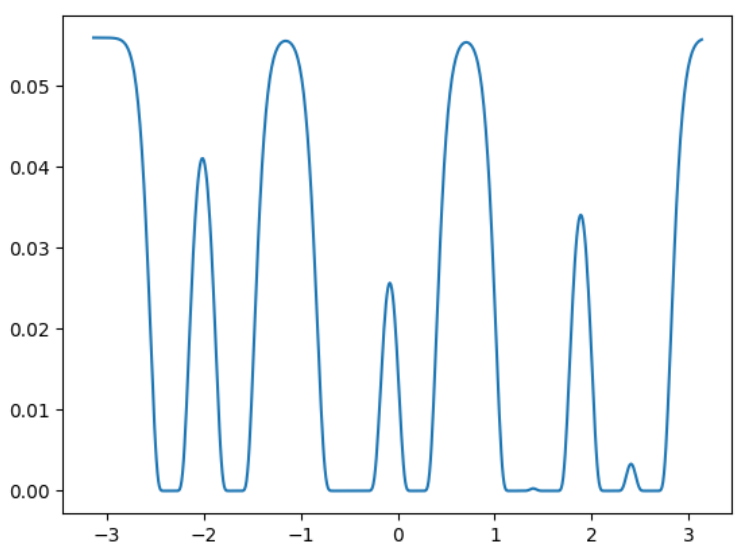
from scipy.stats import norm

ymin = np.min(yi)
z = (ymin - muy)/np.sqrt(sy2).reshape(-1,1)
J = np.sqrt(sy2).reshape(-1,1)*(z*norm.cdf(z)+norm.pdf(z))

next_id = np.argmax(J)
print(next_id,x_act[next_id])

plt.plot(x_act, J)

image.png

ymin = np.min(yi)
z = ymin / np.sqrt(sy2).reshape(-1,1)
J = norm.cdf(z)

plt.plot(x_act, J)

image.png

今までの実装を関数化し、実験計画問題への適用を実装する。

def param_search(xi, yi, gammas = np.array([10,100,1000]), ls=np.arange(0.1,1.5,0.1)):
    """最適なパラメータの探索
    """
    N = len(xi)
    
    lnE = np.zeros((len(gammas), len(ls)))
    for i, g in enumerate(gammas):
        for j, l in enumerate(ls):
            K = RBF_kernel(xi, xi, gamma=g, l=l)
            lnE[i, j]=-N/2*(np.log(2*np.pi/N)+1)-1/2*np.log(np.linalg.det(np.eye(N)+K))-N/2*np.log(yi.T@np.linalg.inv(np.eye(N)+K)@yi)
    idx1, idx2 = np.where(lnE==np.max(lnE))
    best_g = gammas[idx1]
    best_l = ls[idx2]
    print(best_g, best_l)
    return best_g, best_l

def predict(xi, yi, gamma, l):
    """予測分布
    """
    N = len(xi)
    
    # σの推定値
    K_tilde  = RBF_kernel(xi, xi, gamma=gamma, l=l)
    sigma2 = yi.T@np.linalg.inv(np.eye(N)+K_tilde)@yi/N

    # カーネル関数の計算
    K  = sigma2*RBF_kernel(xi, xi, gamma=gamma, l=l)
    K0 = sigma2*RBF_kernel(x_act, x_act, gamma=gamma, l=l)
    k  = sigma2*RBF_kernel(xi, x_act, gamma=gamma, l=l)

    # パラメータの計算
    muy = k.T@np.linalg.inv(K+sigma2*np.eye(N))@yi
    sigmay2 = sigma2 + K0 - k.T@np.linalg.inv(K+sigma2*np.eye(N))@k
    sy2 = np.diag(sigmay2)
    
    return muy, sigma2, sy2

def ei(yi, muy, sy2):
    """EI
    """
    ymin = np.min(yi)
    z = (ymin - muy)/np.sqrt(sy2).reshape(-1,1)
    J = np.sqrt(sy2).reshape(-1,1)*(z*norm.cdf(z)+norm.pdf(z))
    next_id = np.argmax(J)
    return J, next_id

def pi(yi, sy2):
    """PI
    """
    ymin = np.min(yi)
    z = ymin / np.sqrt(sy2).reshape(-1,1)
    J = norm.cdf(z)
    next_id = np.argmax(J)
    return J, next_id

def plot_result(xi, yi, x_act, y_act, muy, sy2, j_ei, p_ei):
    """結果の可視化
    """
    fig, ax = plt.subplots(figsize=(8,4))
    ax2 = ax.twinx()

    # 観測値のプロット
    ax.plot(xi, yi, 'o', c='r')
    ax.plot(x_act, y_act, c='green', alpha=.5)

    # yの予測分布
    ax.plot(x_act, muy, linestyle='--', color='red')
    ax.fill_between(x_act.ravel(),(muy.ravel()+np.sqrt(sy2)),(muy.ravel()-np.sqrt(sy2)), color='red', alpha=.1)

    ax2.plot(x_act, j_ei, alpha=.5)
    ax2.plot(x_act, j_pi, alpha=.5)

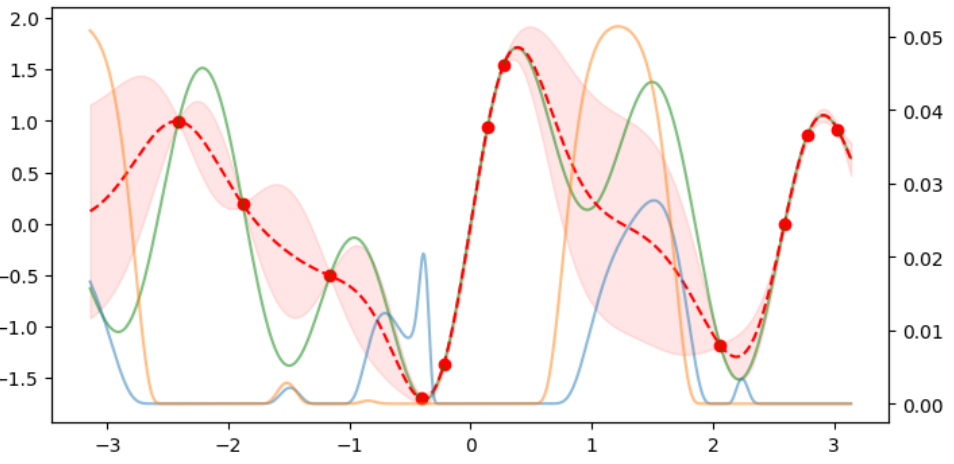
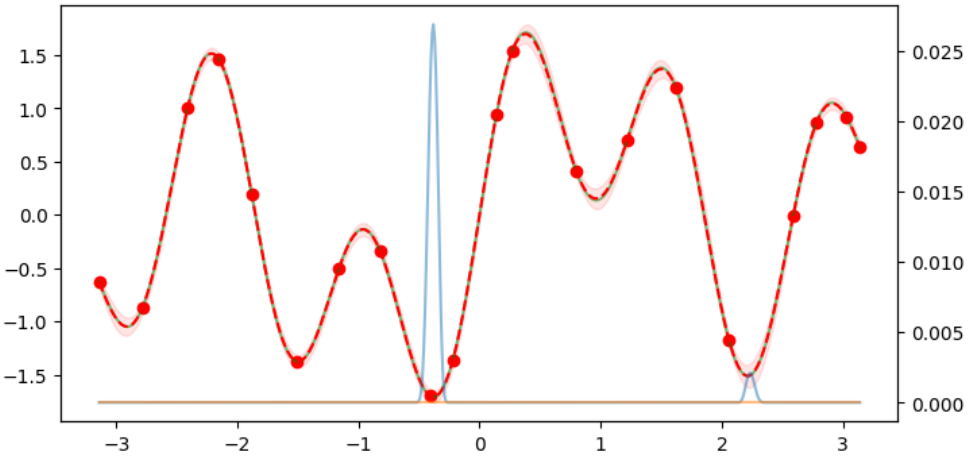
10回の探索を行い、予測分布を導出した結果を示す。
ここでは1,2,10回目のみ示す。
赤い点線が予測分布、緑色の線が実際の値である。
段々と重なっていくことが確認できる。

# ランダムで10点選ぶ
idx = np.sort(np.random.randint(len(x_act), size=10))

# データをサンプリング
xi = x_act[idx]
yi = y_act[idx]

for _ in range(10):
    idx = np.sort(np.append(idx,next_id))

    # データをサンプリング
    xi = x_act[idx]
    yi = y_act[idx]

    best_g, best_l = param_search(xi, yi, gammas = np.array([10,100,1000]), ls=np.arange(0.1,1.5,0.1))
    muy, sigma2, sy2 = predict(xi, yi, gamma=best_g, l=best_l)
    j_ei, _ = ei(yi, muy, sy2)
    j_pi, next_id = pi(yi, sy2)

    plot_result(xi, yi, x_act, y_act, muy, sy2, j_ei, j_pi)
    plt.show()

image.png

image.png

image.png

ガウス過程回帰はschikit-learnにも実装されている。

from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF

#idx = np.sort(np.random.randint(len(x_act), size=10))

#xi = x_act[idx]
#yi = y_act[idx]

model = GaussianProcessRegressor(
    kernel=RBF(1.0, (1e-3, 1e3)),
    alpha=1e-10, 
    optimizer="fmin_l_bfgs_b", 
    n_restarts_optimizer=20,
    normalize_y=True)

model.fit(xi, yi)
y_pred, y_std = model.predict(x_act, return_std=True)

plt.figure(figsize=(8,4))
plt.fill_between(x_act.ravel(),(y_pred+y_std),(y_pred-y_std), alpha=.2)
plt.plot(x_act.ravel(),y_pred)
plt.scatter(xi, yi, c='r')

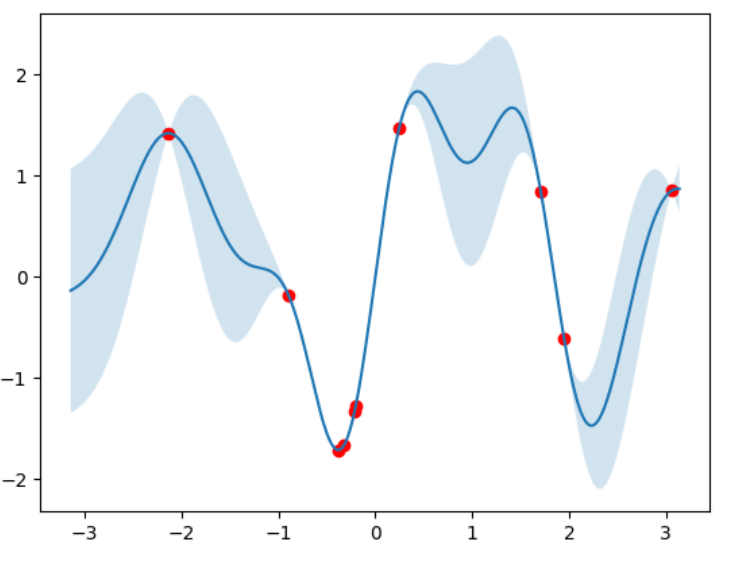
image.png

ベイズ最適化についてはGPyOptというライブラリが提供されている。

import GPy
import GPyOpt

idx = np.sort(np.random.randint(len(x_act), size=10))

for _ in range(10):
    xi = x_act[idx]
    yi = y_act[idx]

    bounds = [{'name': 'x', 'type':'discrete', 'domain':x_act.ravel()}]

    params = {'acquisition_type':'EI',
              'f':None,
              'domain':bounds,
              'model_type':'GP',
              'X':xi,
              'Y':yi,
              'de_duplication':True,
              'normalize_Y':False}
    model = GPyOpt.methods.BayesianOptimization(**params)
    
    next_xi = model.suggest_next_locations()[0][0]
    next_id = np.argmin((x_act-next_xi)**2)
    idx = np.sort(np.append(idx,next_id))
    
    y_mean, y_std = model.model.model.predict(x_act)

    plt.figure(figsize=(8,4))
    plt.plot(x_act, y_mean)
    plt.fill_between(x_act.ravel(),(y_mean.ravel()+y_std.ravel()),(y_mean.ravel()-y_std.ravel()), alpha=.2)
    plt.scatter(xi, yi, c='r')
    plt.show()

image.png

image.png

image.png

以上となります。
ベイズ最適化とともに使うことで、実験データから異常度の高いものは除くことで精度高く推測できるようになる可能性を感じました。

次回

部分空間法による異常検知

3
5
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
3
5