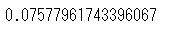「入門 機械学習による異常検知」はRで書かれた異常検知の本です。
今回は実装部分をpythonで書き直していこうと思います。
個人的な勉強のメモ書きとなります。
1章当たりのボリュームが多く、数式もかなりあるためうまくまとまっていません。
また、schikit-learnなどで関数が提供されていれば使っています。
導出や詳細などは「入門 機械学習による異常検知」を読んでいただければと思います。
前回
非正規データからの異常検知
主成分分析による異常検知
異常度の定義
主成分分析により、$M$次元空間の正規直交基底$m$個が$\boldsymbol{u}_1,\cdots,\boldsymbol{u}_m$のように求められたとする。
任意の入力$\boldsymbol{x}'$を直交する2つの成分に分ける。
\boldsymbol{x}'-\hat{\boldsymbol{\mu}}=\boldsymbol{x}'_{(1)}+\boldsymbol{x}'_{(2)}
ここで、$\boldsymbol{x}'{(1)}$は正常部分空間からはみ出る成分、$\boldsymbol{x}'{(2)}$は正常部分空間の成分である。$\hat{\boldsymbol{\mu}}$は標本平均である。
主成分を用いると後者は次のように表せる。
\boldsymbol{x}'_{(2)}=\sum_{i=1}^m\boldsymbol{u}_i\boldsymbol{u}_i^T(\boldsymbol{x}'-\hat{\boldsymbol{\mu}})=U_mU_m^T(\boldsymbol{x}'-\hat{\boldsymbol{\mu}})
ただし、$U_m=[\boldsymbol{u}_1,\cdots,\boldsymbol{u}_m]$と置いた。従って、
\boldsymbol{x}'_{(1)}=(\boldsymbol{x}'-\hat{\boldsymbol{\mu}})-\boldsymbol{x}'_{(2)}=[I_M-U_mU_m^T](\boldsymbol{x}'-\hat{\boldsymbol{\mu}})
となる。$I_M$は$M$次元の単位行列である。
正常部分空間からのはみ出しの大きさ$|\boldsymbol{x}'_{(1)}|^2$が大きいほど異常の度合いは高いと考えられるので、
主成分分析による異常度を次のように定義する。
a_1(\boldsymbol{x}')=|\boldsymbol{x}'_{(1)}|^2=(\boldsymbol{x}'-\hat{\boldsymbol{\mu}})^T[I_M-U_mU_m^T](\boldsymbol{x}'-\hat{\boldsymbol{\mu}})
この量は主成分のみを使って$\boldsymbol{x}'-\hat{\boldsymbol{\mu}}$を表現したときに、どれだけ長さが失われるかを表したものと解釈できる。
この意味で、再構成誤差による異常度と呼ぶことができる。
$M\ll N$の場合、
\tilde{X}=U_r\Lambda_r^{1/2}V_r^T
において、$r=m$とした式に、右から$V_m\Lambda_m^{-1/2}$を掛けられて得られる
U_m=\tilde{X}V_m\Lambda_m^{-1/2}
を使うことで、
a_1(\boldsymbol{x}')=|\boldsymbol{x}'-\hat{\boldsymbol{\mu}}|^2-|\Lambda_m^{-1/2}V_m^T\tilde{X}^T(\boldsymbol{x}'-\hat{\boldsymbol{\mu}})|^2
のように計算できる。
ホテリングのT2との関係
以前出てきた異常度の定義
a(\boldsymbol{x}')=(\boldsymbol{x}'-\hat{\boldsymbol{\mu}})^T\hat{\Sigma}^{-1}(\boldsymbol{x}'-\hat{\boldsymbol{\mu}})
と比べると、共分散行列の逆行列$\hat{\Sigma}^{-1}$に$I_M-U_mU_m^T$が対応していることが分かる。
いま、$\hat{\Sigma}$の階数が$r$がほぼ$m$に等しいとする。
この場合、$S$の$M$個の可能な固有値のうち、$\lambda_1$から$\lambda_m$までがある大きい値となり、それ以降、$\lambda_{m+1}$から$\lambda_M$まではほぼ0となる。後者を$\epsilon$という定数で代表させることにする。
固有値分解より、
\hat{\Sigma}^{-1}=NU_M\Lambda_M^{-1}U_M^T=\sum_{i=1}^m\frac{N}{\lambda_i}\boldsymbol{u}_i\boldsymbol{u}_i^T+\frac{N}{\epsilon}\sum_{j=m+1}^M\boldsymbol{u}_j\boldsymbol{u}_j^T
と表せる。
ここで第2項において、
I_M=U_MU_M^T=\sum_{i=1}^M\boldsymbol{u}_i\boldsymbol{u}_i^T=U_mU_m^T+\sum_{j=1}^M\boldsymbol{u}_j\boldsymbol{u}_j^T
に注意すると、
a_{T^2}(\boldsymbol{x}')=(\boldsymbol{x}'-\hat{\boldsymbol{\mu}})^T\hat{\Sigma_m}^{-1}(\boldsymbol{x}'-\hat{\boldsymbol{\mu}})+\frac{N}{\epsilon}(\boldsymbol{x}'-\hat{\boldsymbol{\mu}})^T[I_M-U_mU_m^T](\boldsymbol{x}'-\hat{\boldsymbol{\mu}})
と書けることが分かる。
ただし、$\hat{\Sigma_m}^{-1}=NU_m\Lambda_m^{-1}U_m^T$と定義した。
$\epsilon$は仮定よりほぼゼロに近い値となるので、その逆数は大きな値となる。
ホテリング理論による異常度は、再構成誤差による異常度でよく近似できることがわかる。
a_{T^2}(\boldsymbol{x}')=\frac{N}{\epsilon}a_1(\boldsymbol{x}')
手順(主成分分析による異常検知)
ステップ1(正常部分空間の計算): 主成分の数$m$を決めておく。また、標本平均$\hat{\boldsymbol{\mu}}$を求め、記憶する。
a. 次元$M$が標本数$N$よりも小さいとき:
散布行列$S$についての固有値方程式を解いて、固有値が大きい順に$(\lambda_1,\boldsymbol{u}_1),\cdots,(\lambda_m,\boldsymbol{u}_m)$のように$m$個求めておく
b. 標本数$N$のほうが次元$M$よりも小さいとき:
グラム行列についての固有値方程式を解いて、固有値が大きい順に、$(\lambda_1,\boldsymbol{v}_1),\cdots,(\lambda_m,\boldsymbol{v}_m)$のように$m$個求めておくステップ2(異常度の計算): 入力$\boldsymbol{x}'$に対して、上記の2通りの場合に対応して異常度$a(\boldsymbol{x}')$を計算する。
a. 次元$M$が標本数$N$よりも小さいとき: 定義に従って異常度を計算する。
a_1(\boldsymbol{x}')=|\boldsymbol{x}'_{(1)}|^2=(\boldsymbol{x}'-\hat{\boldsymbol{\mu}})^T[I_M-U_mU_m^T](\boldsymbol{x}'-\hat{\boldsymbol{\mu}})
b. 標本数$N$の方が次元$M$よりも小さいとき: 定義に従って異常度を計算する。
a_1(\boldsymbol{x}')=|\boldsymbol{x}'-\hat{\boldsymbol{\mu}}|^2-|\Lambda_m^{-1/2}V_m^T\tilde{X}^T(\boldsymbol{x}'-\hat{\boldsymbol{\mu}})|^2
Cars93というデータセットを用いる。
散布行列(S)について異常度の計算を行う。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# 散布行列
S = Xc@Xc.T
# 固有値分解
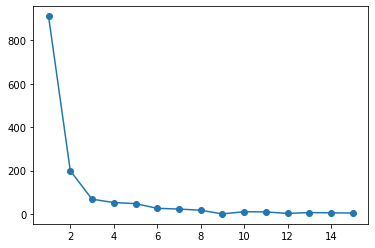
eig_values, eig_vectors = np.linalg.eig(S)
plt.plot(np.arange(1,len(eig_values)+1), eig_values, '-o')
「エルボー則」により、$m=2$とする。
# mの設定
m = 2
# 正常部分空間
x2 = eig_vectors[:,:m].T @ Xc
# 異常度の計算
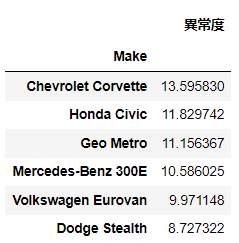
a1 = np.sum(Xc*Xc) - np.sum(x2*x2)
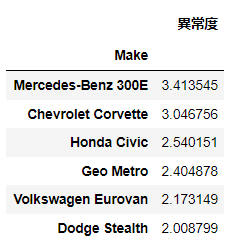
pd.DataFrame(a1, columns=['異常度']).sort_values('異常度', ascending=False).head(6)
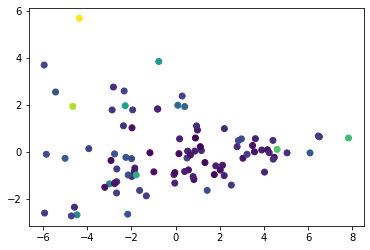
異常度によって色を付けてプロットする。
plt.scatter(np.array(x2).T[:,0], np.array(x2).T[:,1], c=a1)
今回$M<N$ですが、グラム行列でも計算を行い結果の確認を行う。
# グラム行列
G = Xc.T @ Xc
# 固有値分解
eig_values_g, eig_vectors_g = np.linalg.eig(G)
eig_values_g = eig_values_g.real
eig_vectors_g = eig_vectors_g.real
# 定義に従い異常度の計算
Lam_12 = np.diag(eig_values_g[:m]**((-1/2)))
xx2 = Lam_12 @ eig_vectors_g[:,:m].T @ Xc.T @ Xc
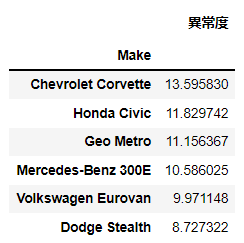
aa1 = np.sum(Xc*Xc) - np.sum(xx2*xx2)
pd.DataFrame(aa1, columns=['異常度']).sort_values('異常度', ascending=False).head(6)
散布行列と同様の結果であることが確認できる。
主成分分析はschikit-learbでも実装されている。
from sklearn.decomposition import PCA
# PCAによる主成分分析
pca = PCA(n_components=2)
X_pca = pca.fit_transform(Xc.T)
# 異常度の計算
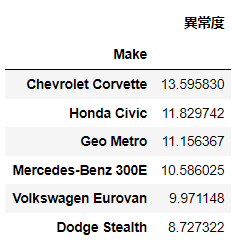
a_pca = np.sum(Xc*Xc) - np.sum(X_pca.T*X_pca.T, axis=0)
pd.DataFrame(a_pca, columns=['異常度']).sort_values('異常度', ascending=False).head(6)
ほぼ同様の結果が得られた。
確率的主成分分析による異常検知
主成分分析の確率的モデル
主成分分析は$M$個の見かけ上の変数$x_1,\cdots,x_M$から、真にアクティブな$m$個の変数$\boldsymbol{z}$を見出す手法である。
確率的主成分分析では、1つの$\boldsymbol{z}$が与えられたときに、観測量$\boldsymbol{x}$が次のように確率的に生成されると考えることである。
p(\boldsymbol{x}|\boldsymbol{z})=N(\boldsymbol{x}|W\boldsymbol{z}+\boldsymbol{\mu},\sigma^2I_M)
ここで、$W$は$M×m$行列で、列空間が正常部分空間に対応する。
$\boldsymbol{\mu}$は観測量$\boldsymbol{x}$の平均値、$\sigma^2$は観測量$\boldsymbol{x}$が生成されるときのばらつきを表すパラメータである。
$I_M$は$M$次元の単位行列である。
さらに、
p(\boldsymbol{z})=N(\boldsymbol{z}|\boldsymbol{0},I_m)
と仮定する。
これはデータとは無関係に設定される分布であり、事前分布と呼ばれる。
確率変数$\boldsymbol{z}$は一般に潜在変数と呼ばれる。
平均ベクトルの推定
$p(\boldsymbol{x}|\boldsymbol{z})$と$p(\boldsymbol{z})$は両者とも正規分布であるから次のような多次元正規分布が導かれる。(参考書参照)
p(\boldsymbol{x})=N(\boldsymbol{x}|\boldsymbol{\mu},C)\ C=WW^T+\sigma^2I_M
対数尤度を計算すると、
\begin{align}
L(\boldsymbol{\mu},W,\sigma^2)&=\sum_{n=1}^N\ln N(\boldsymbol{x}^{(n)}|C)\\
&=\frac{MN}{2}\ln{(2\pi)}-\frac{N}{2}\ln |C|-\frac{1}{2}\sum_{n=1}^N(\boldsymbol{x}^{(n)}-\boldsymbol{\mu})^TC^{-1}(\boldsymbol{x}^{(n)}-\boldsymbol{\mu})
\end{align}
これを$\boldsymbol{\mu}$で偏微分してゼロベクトルと等値することで最尤推定量$\hat{\boldsymbol{\mu}}$が次のように求められる。
\hat{\boldsymbol{\mu}}=\bar{\boldsymbol{x}}=\frac{1}{N}\sum_{n=1}^N\boldsymbol{x}^{(n)}
$W$と$\sigma^2$については複雑な形となっているため、明示的に求めることは難しい。
確率的主成分分析の期待値-最大化法
モデルパラメータ$\Theta={W,\sigma^2}$により定義される周辺尤度
L(\Theta|D)=\sum_{n=1}^N\ln\int d\boldsymbol{z}^{(n)}p(\boldsymbol{x}^{(n)}|\boldsymbol{z}^{(n)},\Theta)p(\boldsymbol{z}^{(n)})
を最大化するようなパラメータ$\Theta=\Theta^*$を求めることを考える。
ここで、和の中身を$L(\Theta|\boldsymbol{x}^{(n)})$と書くこととする。
イエンセンの不等式により対数と積分の順序を交換できる。
$L(\Theta|\boldsymbol{x}^{(n)})$の下界を与える式が得られる。
L(\Theta|\boldsymbol{x}^{(n)})\geq \int d\boldsymbol{z}^{(n)} q(\boldsymbol{z}^{(n)})\ln\frac{p(\boldsymbol{x}^{(n)},\boldsymbol{z}^{(n)}|\Theta)}{q(\boldsymbol{z}^{(n)})}
対数関数が積分変数によらない関数になるとき近似の精度が高くなる。そのときの分布は、
p(\boldsymbol{z}^{(n)}|\boldsymbol{x}^{(n)},\Theta)=N(\boldsymbol{z}^{(n)}|M^{-1}W^T(\boldsymbol{x}-\bar{\boldsymbol{x}}),\sigma^2M^{-1})\\
M=W^TW+\sigma^2I_m
となる。(参考書参照)
以上より対数尤度についての近似式
L(\Theta|D)\sim -\frac{1}{2\sigma^2}\sum_{n=1}^N\bigl\{|\boldsymbol{x}^{(n)}-\bar{\boldsymbol{x}}|^2 - 2(\boldsymbol{x}^{(n)}-\bar{\boldsymbol{x}})^TW<\boldsymbol{z}^{(n)}>+Tr[<\boldsymbol{z}^{(n)}\boldsymbol{z}^{(n)T}>W^TW]+\sigma^2Tr[<\boldsymbol{z}^{(n)}\boldsymbol{z}^{(n)T}>] \bigr\}-\frac{MN}{2}\ln{(2\pi\sigma^2)}+const.
が得られる。$<・>$は$q(\boldsymbol{z}^{(n)})$による期待値を表す。
仮置きのパラメータ$\Theta'$に関連する項は、
<\boldsymbol{z}^{(n)}>=M'^{-1}W'^T(\boldsymbol{x}^{(n)}-\bar{\boldsymbol{x}})\\
<\boldsymbol{z}^{(n)}\boldsymbol{z}^{(n)T}>={\sigma^2}' M'^{-1}+<\boldsymbol{z}^{(n)}><\boldsymbol{z}^{(n)}>^T
ただし、$M'=W'^TW'+{\sigma^2}'I_m$である。
各パラメータで微分してゼロと置くと、各パラメータの更新式が次のように求まる。
W=\biggl\{\sum_{n=1}^N(\boldsymbol{x}^{(n)}-\bar{\boldsymbol{x}})<\boldsymbol{z}^{(n)T}> \biggl\}\biggl(\sum_{n=1}^N<\boldsymbol{z}^{(n)}\boldsymbol{z}^{(n)T}> \biggr)^{-1}\\
\sigma^2=\frac{1}{NM}\sum_{n=1}^N\bigl\{|\boldsymbol{x}^{(n)}-\bar{\boldsymbol{x}}|^2 - 2(\boldsymbol{x}^{(n)}-\bar{\boldsymbol{x}})^TW<\boldsymbol{z}^{(n)}>+Tr[<\boldsymbol{z}^{(n)}\boldsymbol{z}^{(n)T}>W^TW] \bigr\}
手順(期待値-最大化法による確率的主成分分析モデルの推定)
- $\mu$の決定:$\boldsymbol{\mu}$を
\hat{\boldsymbol{\mu}}=\bar{\boldsymbol{x}}=\frac{1}{N}\sum_{n=1}^N\boldsymbol{x}^{(n)}
により、$\boldsymbol{x}$の標本平均として求める。
2. 初期化:パラメータ$W,\sigma^2$の初期推定値を適当に与える
3. 反復:$t=0,1,2,\cdots$について、収束するまで以下を繰り返す。
a.現在のパラメータ推定値$\Theta'$を用いて、各データ点ごとに
<\boldsymbol{z}^{(n)}>=M'^{-1}W'^T(\boldsymbol{x}^{(n)}-\bar{\boldsymbol{x}})\\
<\boldsymbol{z}^{(n)}\boldsymbol{z}^{(n)T}>={\sigma^2}' M'^{-1}+<\boldsymbol{z}^{(n)}><\boldsymbol{z}^{(n)}>^T
を計算する。
b.上記で求めた$<\boldsymbol{z}^{(n)}>$および$<\boldsymbol{z}^{(n)}\boldsymbol{z}^{(n)T}>$を用いて、
W=\biggl\{\sum_{n=1}^N(\boldsymbol{x}^{(n)}-\bar{\boldsymbol{x}})<\boldsymbol{z}^{(n)T}> \biggl\}\biggl(\sum_{n=1}^N<\boldsymbol{z}^{(n)}\boldsymbol{z}^{(n)T}> \biggr)^{-1}\\
\sigma^2=\frac{1}{NM}\sum_{n=1}^N\bigl\{|\boldsymbol{x}^{(n)}-\bar{\boldsymbol{x}}|^2 - 2(\boldsymbol{x}^{(n)}-\bar{\boldsymbol{x}})^TW<\boldsymbol{z}^{(n)}>+Tr[<\boldsymbol{z}^{(n)}\boldsymbol{z}^{(n)T}>W^TW] \bigr\}
により、$W,\sigma^2$を更新する。
次元数$m$の決定
例えば、
BIC(M_k)=-2(最尤推定をしたときの対数尤度の値)+M_k\ln N
で与えられる**ベイズ情報量基準(BIC)**を使うとする。
$W,\boldsymbol{\mu},\sigma$に含まれるパラメータの数は、それぞれ$Mm-m(m-1)/2,m,1$なので、
BIC_{PPCA}=-2L(\hat{\Theta}|D)+\biggl\{Mm-\frac{m(m-1)}{2}+m+1 \biggr\}\ln N
となる。
$\hat{\Theta}$は期待値-最大化法により推定されたパラメータである。
このBICが最小になる$m$を用いるのが一つの合理的な方法となる。
確率的主成分分析による異常度の定義
新しいデータ$\boldsymbol{x}'$に対する異常度は、
a(\boldsymbol{x}')=(\boldsymbol{x}'-\hat{\boldsymbol{\mu}})^T\hat{C}^{-1}(\boldsymbol{x}'-\hat{\boldsymbol{\mu}})
と定義できる。
手順(確率的主成分分析による異常検知)
- 正常と思われる$N$個の$M$次元データ$D={\boldsymbol{x}^{(1)},\cdots,\boldsymbol{x}^{(N)}}$を用意する
- 手動またはBICなどの手法により、削減後の次元数$m$を決める
- データに確率的主成分分析を適用し、パラメータの最尤推定値$\hat{\Theta}={\hat{W},\hat{\boldsymbol{\mu}},\hat{\sigma}^2 }$を得る
- 正常・異常を判定したいデータ$\boldsymbol{x}'$ごとに、異常度$a(\boldsymbol{x}')$を計算する。
X = np.array(Xc)
# 次元数
M = X.shape[0]
N = X.shape[1]
# 今回はmは手動で設定
m = 2
# 平均値の決定
mu = X.mean(axis=1).reshape((M, -1))
# 初期値の設定
W = np.random.normal(size=(M, m))
sig2 = np.random.rand(1)
# 繰り返し更新
for t in range(140):
# Mの計算
M_dash = W.T@W + sig2*np.eye(m)
# Znの計算
zn = np.array([np.linalg.inv(M_dash) @ W.T @ (X[:,n].reshape((M, -1)) - mu) for n in range(N)])
znznT = sig2 * np.array([np.linalg.inv(M_dash) + zn[n]@zn[n].T for n in range(N)])
# W, σの更新
W = np.array([(X[:,n].reshape((M, -1))-mu)@zn[n].T for n in range(N)]).sum(axis=0) @ np.linalg.inv(znznT.sum(axis=0))
sig2 = np.array([np.sum((X[:,n].reshape((M, -1)) - mu)**2) - 2*(X[:,n].reshape((M, -1)) - mu).T@W@zn[n] + np.trace(znznT[n]@W.T@W) for n in range(N)]).sum() / (N*M)
# Cの計算
C = W@W.T + sig2*np.eye(M)
# 異常度の計算
a2 = [(X[:,n]).T@np.linalg.inv(C)@(X[:,n]) for n in range(N)]
a_list = pd.DataFrame(a2, columns=['異常度'], index=Xc.columns).sort_values('異常度', ascending=False).head(6)
a_list
正規直交基底を求めるためにはQR分解などを行う。
from scipy import linalg
# グラム・シュミット直交化関数
# https://python.atelierkobato.com/schmidt/
def schmidt(arr):
# 配列のデータ型を64バイト浮動小数点数型に変換
arr = np.array(arr, dtype=np.float64)
# 渡した配列の列数(基底に含まれるベクトル数)
k = arr.shape[1]
# 1列目のベクトルを選択
u = arr[:,[0]]
# uを正規化
q = u / linalg.norm(u)
# シュミットの直交化
for j in range(1, k):
u = arr[:,[j]]
for i in range(j):
u -= np.dot(q[:,i], arr[:,j]) * q[:,[i]]
qi = u / linalg.norm(u)
q = np.append(q, qi, axis=1)
return q
# グラムシュミットの直交化
W_qr = schmidt(W)
x3 = W_qr.T@(X)
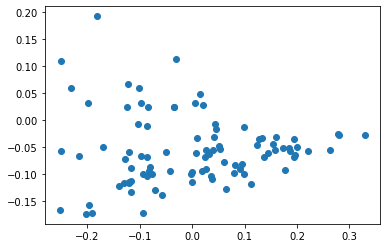
plt.scatter(np.array(x3)[0], np.array(x3)[1], c=a2)
カーネル主成分分析による異常検知
正常部分空間の算出
$N$個の$M$次元データ$D={\boldsymbol{x}^{(1)},\cdots,\boldsymbol{x}^{(N)}}$には、異常が全く含まれていないか、含まれていても圧倒的少数と信じられるとする。
この$M$次元の標本ぞれぞれを、$M_{\phi}$空間に移すような変換を$\phi$と表す。
一般に$M_{\phi}$としては$M$よりもかなり大きい数を想定し、標本数$N$に対して$M_{\phi} \gg N$が成り立つ状況を想定する。
非線形変換$\boldsymbol{x}→\phi(\boldsymbol{x})$により、元データ$D$は、新しいデータ$D_{\phi}={\phi^{(1)},\cdots,\phi^{(N)} }$に変換される。
ここで、$\phi^{(n)}$は$\phi(\boldsymbol{x}^{(n)})$を表す。
このデータに対してデータ行列
\Phi=[\phi^{(1)},\cdots,\phi^{(N)}]\ および\ \tilde{\Phi}=\Phi H_N
を定義する。
これにより
H_NKH_N\boldsymbol{v}=\lambda\boldsymbol{v}
という固有方程式が成り立つ。ただす、$k$は$K=\Phi^T\Phi$で定義される$N×N$行列であり、$(i,j)$成分は$\phi^{(i)T}\phi^{(j)}$である。
固有方程式を解いて、固有値の大きい順から$m$個の固有値と固有ベクトルの組$(\lambda_1,\boldsymbol{v}_1),\cdots,(\lambda_m,\boldsymbol{v}_m)$を求めたとする。すると、正常部分空間の基底が
U_m=[\boldsymbol{u}_1,\cdots,\boldsymbol{u}_m]=\tilde{\Phi}V_m\Lambda_m^{-1/2}=\Phi H_NV_m\Lambda_m^{-1/2}
のように得られる。$V_m=[\boldsymbol{v}_1,\cdots,\boldsymbol{v}_m]$である。
上式から$M$次元の任意の入力$\boldsymbol{x}'$が、正常部分空間において次のような$m$次元ベクトル$\boldsymbol{z}'$として表されることがわかる。
\boldsymbol{z}'=\Lambda_m^{-1/2}V_m^TH_N\boldsymbol{k}(\boldsymbol{x}')
ただし、$N$次元ベクトル$\boldsymbol{k}(\boldsymbol{x}')$の第$n$成分は、$\phi^{(n)T}\phi(\boldsymbol{x}')$で定義される。
ここで、ある関数$k$を使って次のような置き換えを行う。
(1)$K$の$(i,j)$成分をカーネル関数$k(\boldsymbol{x}^{(i)},\boldsymbol{x}^{(j)})$で置き換える($i,j=1,\cdots,N$)
(2)$\boldsymbol{k}(\boldsymbol{x}')$の第$i$成分をカーネル関数$k(\boldsymbol{x}^{(i)},\boldsymbol{x}^{(j)})$で置き換える($i=1,\cdots,N$)
このような置換を行った主成分分析をカーネル主成分分析と呼ぶ。
実行例
手順(カーネル主成分分析による主部分空間の計算)
データ$D={\boldsymbol{x}^{(1)},\cdots,\boldsymbol{x}^{(N)}}$を用意する。また、カーネル関数$k$の関数形と、主成分の数$m$を決めておく。
- $(i,j)$成分が$k(\boldsymbol{x}^{(i)},\boldsymbol{x}^{(j)})$で与えられる$N×N$行列$K$を作る
- $H_NKH_N$の固有値分解を行い、固有値が大きい順に$m$個の固有値と固有ベクトルの組$(\lambda_1,\boldsymbol{v}_1),\cdots,(\lambda_m,\boldsymbol{v}_m)$を求める。
- 固有ベクトルを並べた行列$V_m=[\boldsymbol{v}_1,\cdots,\boldsymbol{v}_m]$と、固有値を対角行列にもつ行列$\Lambda=diag(\lambda_1,\cdots,\lambda_m)$を記憶する
- 必要に応じて、次元削減後の座標を求める
def RBF(x1, x2, sig):
return np.array([[np.exp(-sig*np.sum((xx1-xx2)**2)) for xx1 in x1] for xx2 in x2])
# カーネル行列の計算
K = RBF(Xc.T, Xc.T, 0.001)
Hn = np.eye(N) - np.ones((N,N))/N
# 固有値分解
eig_values, eig_vectors = np.linalg.eig(Hn@K@Hn)
V = eig_vectors[:,:m]
Lam = np.diag(eig_values[:m]**((-1/2)))
lam = np.diag(eig_values[:m])
# 正常部分空間
Xkpca = Lam @ V.T @ Hn @ K.T
plt.scatter(Xkpca[0], Xkpca[1])
from sklearn.decomposition import KernelPCA
kpca = KernelPCA(kernel="rbf", gamma=0.001, n_components=2)
X_kpca = kpca.fit_transform(Xc.T)
plt.scatter(X_kpca[:,0], X_kpca[:,1])
異常度の定義(m=1)
異常度は
a_1(\boldsymbol{x}')=k(\boldsymbol{x}',\boldsymbol{x}')-\boldsymbol{k}(\boldsymbol{x}')^TH_NV_m\Lambda_m^{-1}V_m^TH_N\boldsymbol{k}(\boldsymbol{x}')
となる。
カーネル主成分分析では、次元削減後のベクトルが非常に敏感であることが知られており、注意深くパラメータを選択する必要がある。
この点に対応するため、実用上問題設定を若干拡張することが試みられている。
ポイントは2点ある。
1つ目は、ある一定期間データを取得し続けるなどして、データ点の集合$D'=\boldsymbol{x}'^{(1)},\cdots,\boldsymbol{x}'^{(N')}$を取得し、$D'$全体の様子を、正常時のデータ$D$と比べるという考えかたである。
2つ目は、$D'$を$D$と比べるに当たり、おのおのから抽出された主成分同士で比較することである。
$D'$から$D'_{\phi}$を非線形変換により得たとする。
データ行列は次のように表すこととする。
\Psi=[\phi'^{(1)},\cdots,\phi'^{(N')}]\ および\ \tilde{\Psi}=\Psi H_{N'}
固有方程式
H_{N'}K'H_{N'}\boldsymbol{r}=\gamma \boldsymbol{r}
を解いて、固有ベクトルと固有値からなる行列を
R_m=[\boldsymbol{r}_1,\cdots,\boldsymbol{r}_m]\\
\Gamma_m=diag (\gamma_1,\cdots,\gamma_m)
のように定義する。ただし、$K'$は$(i,j)$成分が$k(\boldsymbol{x}'^{(i)},\boldsymbol{x}'^{(j)})$で与えられる$N'×N'$行列である。
これらを用いて、$D'_{\phi}$に基づく主部分空間が
Q_m=[\boldsymbol{q}_1,\cdots,\boldsymbol{q}_m]=\tilde{\Psi}R_m\Gamma_m^{-1/2}=\Psi H_{N'}R_m\Gamma_m^{-1/2}
のように得られる。
異常度は、「正常部分空間からのはみ出しの長さ2乗」として定義することができる。
簡単な場合として$m=1$の状況を考える。
正常部分空間を表す$M_{\phi}$次元のベクトル$\boldsymbol{u}1$と、$D'$から求めた$M{\phi}$次元の主成分ベクトル$\boldsymbol{q}_1$の食い違いを評価するという問題になる。
a_{m=1}(D,D')=1-(\boldsymbol{u}_1^T\boldsymbol{q}_1)^2
という定義が自然に考えられる。
カーネル主成分分析では非線形写像が明示的に与えられていないので、$M_{\phi}$次元の量を使わずに表す必要がある。
a_{m=1}(D,D')=1-\frac{\boldsymbol{v}_1^T}{\sqrt{\lambda_1}}H_NBH_{N'}\frac{\boldsymbol{r}_1}{\sqrt{\gamma_1}}
となる。$B$は$D$と$D'$をつなぐカーネル行列であり
B=\Phi^T\Psi\ すなわち\ B_{i,j}=k(\boldsymbol{x}^{(i)},\boldsymbol{x}'^{(j)})
と定義される。
異常度の定義(m>1)
$m=1$の自然な拡張として次のように異常度を定義する。
a(D,D')=1-|U_m^TQ_m|_2^2
ここで、$||_2$は行列2ノルムと呼ばれる量である。
定義(行列ノルム)
$(i,j)$要素を$A_{i,j}$とする$I×J$行列Aのフロベニウスノルム$|A|_F$を以下で定義する。
|A|_F=\sqrt{\sum_{i=1}^I\sum_{j=1}^JA_{i,j}^2}
同じく、行列Aの行列$p$ノルム$|A|_p$を、ベクトル$p$ノルムを用いて次で定義する。
|A|_p=\max_{\boldsymbol{\varphi}}\frac{|A\boldsymbol{\varphi}|_p}{|\boldsymbol{\varphi}|_p}
ただし右辺の$\boldsymbol{\varphi}$は$J$次元ベクトルである。
$\boldsymbol{\varphi}$は$A^TA$の最大固有値に属する固有ベクトルとなる。
また、行列2ノルムは最大特異値に等しいことが分かる。
異常度の式には$M_{\phi}×m$行列$U_m$が入っており、非線形変換が明示的に与えられていない状況だと計算できないので、書き換えを行う。
\Omega=U_m^TQ_m=\Lambda_m^{-1/2}V_m^TH_NBH_{N'}R_m\Gamma_m^{-1/2}
であることが分かる。
結局、異常度は
a(D,D')=1-(\Omegaの最大特異値)^2
と計算できる。
def calc_eigen(X):
N = X.shape[0]
K = RBF(X, X, 0.1)
Hn = np.eye(N) - np.ones((N,N))/N
eig_values, eig_vectors = np.linalg.eig(Hn@K@Hn)
R = eig_vectors[:,:m]
Gamma = np.diag(eig_values[:m]**((-1/2)))
return Hn, R, Gamma
前の分析で異常と判定されていたデータを異常データとし計算を子なう。
X1 = np.array(Xc).T[Xc.columns.isin(a_list.index)] # 異常データ
X2 = np.array(Xc).T[~Xc.columns.isin(a_list.index)][:40] # 正常データ1
X3 = np.array(Xc).T[~Xc.columns.isin(a_list.index)][:46] # 正常データ2
def calc_a(X1, X2):
Hn1, R1, Gamma1 = calc_eigen(X1)
Hn2, R2, Gamma2 = calc_eigen(X2)
B = RBF(X2, X1, 0.1)
Omega = Gamma1@R1.T@Hn1@B@Hn2@R2@Gamma2
return 1 - np.linalg.eig(Omega)[0][0].real**2
正常データのみで計算を行う。
calc_a(X2, X3)
異常データを含めて計算を行う。
X12 = np.concatenate([X1, X2])
calc_a(X12, X3)
次回
入力と出力のあるデータからの異常検知
参考文献