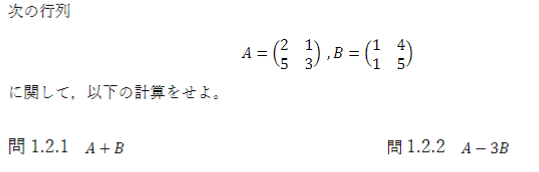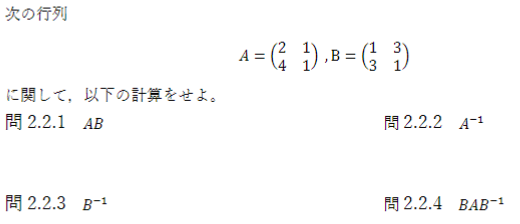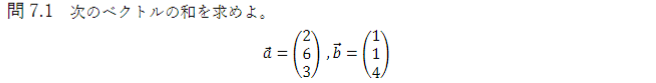ラビットチャレンジレポート1 応用数学

1. 線形代数

1.1 要約

1.1.1 固有値・固有ベクトル

スカラーとは、大きさなどを表す数で、四則演算が可能である。
ベクトルとは、「大きさ」と「向き」をもち矢印で図示される量である。
ベクトルは次のように表します。

\left(\begin{matrix} 
x \\ 
y  
\end{matrix}\right)

行列はスカラーを表にしたもの、またはベクトルを並べたもののことである。
行列は次のように表します。

\left(\begin{matrix} 
a&b \\ 
c&d  
\end{matrix}\right)

ベクトルは、行列と積をとることで他のベクトルに変換される。

\left(\begin{matrix} 
a & b \\ 
c & d 
\end{matrix}\right)
\left(\begin{matrix} 
x \\ 
y  
\end{matrix}\right)
=
\left(\begin{matrix} 
ax+by \\ 
cx+dy  
\end{matrix}\right)

スカラーでいう逆数のような行列を逆行列と呼び、$A^{-1}$と表す。
行列とその逆行列の積は単位行列となる。

AA^{-1}=I

行列式は次にように定義される値である。

\begin{vmatrix}
 a & b \\
 c & d 
\end{vmatrix}
=ad-bc

また、3次元以上の行列も2次元の行列式の和に展開することができる。

\begin{vmatrix}
 a & b & c\\
 d & e & f\\
 g & h & i 
\end{vmatrix}
=a
\begin{vmatrix}
 e & f \\
 h & i 
\end{vmatrix}
-d
\begin{vmatrix}
 b & c \\
 h & i 
\end{vmatrix}
+g
\begin{vmatrix}
 b & c \\
 e & f 
\end{vmatrix}

行列式の性質としては、

• 同じ行ベクトルが含まれるとゼロ
• 1つの行ベクトルがλ倍されると行列式もλ倍される
• i番目の行ベクトルだけが違う場合、それぞれの行列式を足し合わせたものと、その行ベクトルのみを足し合わせた行列の行列式は等しくなる
• 行を入れ替えると符号が変わる

行列式がゼロの場合、その行列は逆行列を持たない。

ある行列$A$に対して、以下の式が成り立つとき、
ベクトル$\boldsymbol{x}$とその係数$\lambda$を、行列$A$に対する固有ベクトル、固有値と呼ぶ。

A\boldsymbol{x}=\lambda\boldsymbol{x}

例えば次の式において、左辺の行列の固有ベクトルは$(1,1)^T$、固有値は5となる。

\left(\begin{matrix} 
1 & 4 \\ 
2 & 3 
\end{matrix}\right)
\left(\begin{matrix} 
1 \\ 
1  
\end{matrix}\right)
=
5
\left(\begin{matrix} 
1 \\ 
1  
\end{matrix}\right)

求め方は次のようになる。

A\boldsymbol{x}=\lambda\boldsymbol{x}\\
(A-\lambda I)\boldsymbol{x}=\boldsymbol{0}\\
\boldsymbol{x}\neq\boldsymbol{0}より\\
|A-\lambda I|=0

(例)　
$
\left(\begin{matrix}
3 & 2 & 0\
0 & 2 & 0\
0 & 0 & 1
\end{matrix}\right)
$の固有値、固有ベクトルを求める。

|A-\lambda I|=0より\\
\begin{vmatrix}
 3-\lambda & 2 & 0\\
 0 & 2-\lambda & 0\\
 0 & 0 & 1-\lambda 
\end{vmatrix}
=0\\
(3-\lambda)(2-\lambda)(1-\lambda)=0\\
\lambda = 3,2,1

1. $\lambda=3$

\left(\begin{matrix} 
0 & 2 & 0\\ 
0 & -1 & 0\\
0 & 0 & -2
\end{matrix}\right)
\left(\begin{matrix} 
x_1 \\ 
x_2 \\
x_3 
\end{matrix}\right)
=0より\,
\boldsymbol{x}=c_1\left(\begin{matrix} 
1 \\ 
0 \\
0 
\end{matrix}\right)

1. $\lambda=2$

\left(\begin{matrix} 
1 & 2 & 0\\ 
0 & 0 & 0\\
0 & 0 & -1
\end{matrix}\right)
\left(\begin{matrix} 
x_1 \\ 
x_2 \\
x_3 
\end{matrix}\right)
=0より\,
\boldsymbol{x}=c_2\left(\begin{matrix} 
2 \\ 
-1 \\
0 
\end{matrix}\right)

1. $\lambda=1$

\left(\begin{matrix} 
2 & 2 & 0\\ 
0 & 1 & 0\\
0 & 0 & 0
\end{matrix}\right)
\left(\begin{matrix} 
x_1 \\ 
x_2 \\
x_3 
\end{matrix}\right)
=0より\,
\boldsymbol{x}=c_3\left(\begin{matrix} 
0 \\ 
0 \\
1 
\end{matrix}\right)\\

1.1.2 固有値分解

固有値を対角線上に並べた行列

\Lambda=\left(\begin{matrix} 
\lambda_1 &  & \\ 
 & \lambda_2 & \\
 &  &  \ddots
\end{matrix}\right)

それに対する固有ベクトルを並べた行列

V=\left(\begin{matrix} 
\boldsymbol{v_1} & \boldsymbol{v_2} & \cdots
\end{matrix}\right)

としたときに

AV=V\Lambda

と関係づけられ、従って以下のように変形できる。

A=V\Lambda V^{-1}

このように正方行列を3つの行列の積に変換することを固有値分解と呼ぶ。

1.1.3 特異値分解

正方行列以外に固有値分解のようなことを行う。

M\boldsymbol{v}=\sigma\boldsymbol{u}\\
M^T\boldsymbol{u}=\sigma\boldsymbol{v}

という特殊な単位ベクトルが存在すれば、以下のような特異値分解ができる。

M=USV^{-1}

ここで、

M^TM\boldsymbol{v}=\sigma M^T\boldsymbol{u}=\sigma^2\boldsymbol{v}\\
MM^T\boldsymbol{u}=\sigma M\boldsymbol{v}=\sigma^2\boldsymbol{u}

行列で考えると、

MV=US\\
M=USV^{-1}

また、

M^TU=VS^T\\
M^T=VS^TU^{-1}

これらの積は、

MM^T=USV^{-1}VS^TU^{-1}=USS^TU^{-1}\\
M^TM=VS^TU^{-1}USV^{-1}=VS^TSV^{-1}

$MM^T$ を固有値分解すれば、左特異ベクトル$U$と特異値の2乗が、
$M^TM$を固有値分解すれば、右特異ベクトル$V$と特異値の2乗が求められる。

1.3 演習

1.1

1.1.1

a+b=
\left(\begin{matrix} 
1 \\ 
6 \\
3
\end{matrix}\right) +
\left(\begin{matrix} 
5 \\ 
2 \\
4
\end{matrix}\right) =
\left(\begin{matrix} 
6 \\ 
8 \\
7
\end{matrix}\right)

1.1.2

a+b=
\left(\begin{matrix} 
1 \\ 
6 \\
3
\end{matrix}\right) -
\left(\begin{matrix} 
5 \\ 
2 \\
4
\end{matrix}\right) =
\left(\begin{matrix} 
-4 \\ 
4 \\
1
\end{matrix}\right)

1.1.3

7a=
7\left(\begin{matrix} 
1 \\ 
6 \\
3
\end{matrix}\right) =
\left(\begin{matrix} 
7 \\ 
42 \\
21
\end{matrix}\right)

1.1.4
1.1.1の計算結果を利用する。

8(a+b)=
8\left(\begin{matrix} 
6 \\ 
8 \\
7
\end{matrix}\right) =
\left(\begin{matrix} 
48 \\ 
64 \\
56
\end{matrix}\right)

1.2

1.2.1

A+B=
\left(\begin{matrix} 
2&1 \\ 
5&3 
\end{matrix}\right) +
\left(\begin{matrix} 
1&4 \\ 
1&5 
\end{matrix}\right) =
\left(\begin{matrix} 
3&5 \\ 
6&8 
\end{matrix}\right)

1.2.2

A-3B=
\left(\begin{matrix} 
2&1 \\ 
5&3 
\end{matrix}\right) -
3\left(\begin{matrix} 
1&4 \\ 
1&5 
\end{matrix}\right) =
\left(\begin{matrix} 
-1&-11 \\ 
2&-12 
\end{matrix}\right)

2.1

2.1.1

A\boldsymbol{u}= 
\begin{pmatrix}
 1 & 3 & 4\\
 5 & 9 & 0\\
 3 & 1 & 2 
\end{pmatrix}
\begin{pmatrix}
 1\\
 0\\
 3 
\end{pmatrix}=
\begin{pmatrix}
 13\\
 5\\
 9
\end{pmatrix}

2.1.2

B\boldsymbol{u}= 
\begin{pmatrix}
 1 & 0 & 3\\
 0 & 2 & 5
\end{pmatrix}
\begin{pmatrix}
 1\\
 0\\
 3 
\end{pmatrix}=
\begin{pmatrix}
 10\\
 15
\end{pmatrix}

2.1.3

BA= 
\begin{pmatrix}
 1 & 0 & 3\\
 0 & 2 & 5
\end{pmatrix}
\begin{pmatrix}
 1 & 3 & 4\\
 5 & 9 & 0\\
 3 & 1 & 2 
\end{pmatrix}=
\begin{pmatrix}
 10&6&10\\
 25&23&10
\end{pmatrix}

2.1.4

B^T= 
\begin{pmatrix}
 1 & 0 & 3\\
 0 & 2 & 5
\end{pmatrix}^T=
\begin{pmatrix}
 1&0\\
 0&2\\
 3&5
\end{pmatrix}

2. 確率

2.1 要約

2.1 確率

• 頻度確率　発生する頻度
  例「10本のうち1本だけ当たりであるくじを引いて確率を調べたところ10%であった。」

• ベイズ確率　信念の度合い
  例「あなたが風邪である確率は40%です。」

確率の定義を示す。

P(A)=\frac{n(A)}{n(U)}=\frac{事象Aが起こる数}{すべての事象の数}\\
0\leq P(A)\leq1

ここで、Aが起こらない（$\bar{A}$の）確率は

P(\bar{A})=\frac{n(U)-n(A)}{n(U)}=1-P(A)

となる。

共通部分の確率(同時確率)は

P(A \cap B)=P(A)P(B|A)

と表せる。$P(B|A)$はAであるという条件の下で、Bである確率のこと。
$A\cap B$と$B\cap A$は等しいので、

P(A \cap B)=P(B \cap A)=P(B)P(A|B)

とも表すことができる。

ここで、ある事象Bが与えられたもとで、Aとなる確率$P(A|B)$を条件付き確率と呼ぶ。

P(A|B)=\frac{P(A\cap B)}{P(B)}=\frac{n(A\cap B)}{n(B)}

事象Aと事象Bについて、お互いの発生に因果関係がない（独立な事象）場合、

P(A\cap B)=P(A)P(B|A)=P(A)P(B)

次に、和集合について考える。
和集合の確率は、

P(A\cup B)=P(A)+P(B)-P(A\cap B)

となる。

ベイズ則

ある子どもは毎日1/4の確率でお菓子をもらえる。もらった子どもは1/2の確率で喜ぶ。喜んでいる子どもがお菓子をもらった確率を求める。（子どもが何もなくても喜んでいる確率は1/3とする。）

P(A)P(B|A)=P(B)P(A|B)

P(お菓子)=1/4 \quad P(喜ぶ|お菓子)=1/2 \quad P(喜ぶ)=1/3\\
P(喜ぶ|お菓子)×P(お菓子)=P(喜ぶ,お菓子)\\
P(喜ぶ,お菓子)=P(お菓子,喜ぶ)\\
P(お菓子,喜ぶ)=P(お菓子|喜ぶ)×P(喜ぶ)

したがって、

P(お菓子|喜ぶ)=\frac{P(喜ぶ|お菓子)×P(お菓子)}{P(喜ぶ)}\\
=\frac{(1/2)×(1/4)}{1/3}=3/8

2.2 統計

• 記述統計　集団の性質を要約し記述する

• 推測統計　集団から一部（標本）を取り出し母集団の性質を推測する

• 確率変数　事象と結びつけられた数値（コインの表が1、裏が0など。）。事象そのものを指す場合もある。

• 確率分布　事象の発生する確率の分布

例　コインを4枚投げ、表の出る回数を考える

事象	表が4枚	表が3枚	表が2枚	表が1枚	表が0枚
確率変数(表の数)	4	3	2	1	0
事象が発生した回数	75	300	450	300	75
確率	1/16	4/16	6/16	4/16	1/16

期待値

その分布における確率変数の平均値（ありえそうな値）
期待値$E(f)$は
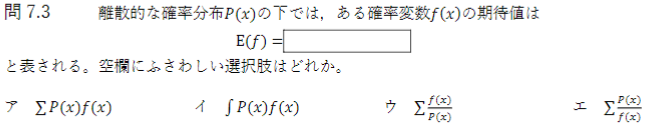
離散変数の場合

E(f)=\sum_{k=1}^nP(X=x_k)f(X=x_k)

連続変数の場合

E(f)=\int_{k=1}^nP(X=x)f(X=x)dx

分散と共分散

• 分散　データの散らばり具合。期待値からのずれの平均。

\begin{align}
Var(f)&=E\bigr((f_{(X=x)}-E(f))^2 \bigl)\\
&=E(f^2_{(X=x)})-(E(f))^2
\end{align}

• 共分散　2つのデータ系列の傾向の違い
  　 　　　正の値をとれば似た傾向、負の値であれば逆の傾向

\begin{align}
Cov(f)&=E\bigr((f_{(X=x)}-E(f))(g_{(Y=y)}-E(g))\bigl)\\
&=E(fg)-E(f)E(g)
\end{align}

• 標準偏差　分散はの平方根をとったもの。分散は2乗しているため単位が異なる。

確率分布

• ベルヌーイ分布　例えばコインを投げて表と裏が出る確率を表す分布

P(x|\mu)=\mu^x(1-\mu)^{1-x}

• マルチヌーイ分布　例えばサイコロの各面が出る確率の分布
• 二項分布　ベルヌーイ分布の多試行版
  　確率$\lambda$で起こる事象が試行$n$回のうち$x$回起こる確率の分布

P(x|\lambda, n)=\frac{n!}{x!(n-x)!}\lambda^x(1-\lambda)^{n-x}

• ガウス分布　釣鐘型の連続分布

N(x|\mu,\sigma)=\sqrt{\frac{1}{2\pi\sigma^2}}\exp{\bigr(-\frac{1}{2\sigma^2(x-\mu)^2}\bigl)}

2.3 演習

3.1

a: さいころの目は「さいころを振る」という試行の結果として得られる数値であるから確率変数といえる。
b. コインの枚数は試行の条件として事前に決めるものであり、結果として得られる数値ではない。確率変数とはいえない 。
c. 色は数値ではないため、確率変数とはいえない。「赤の個数」などは確率変数として扱える。
d. 回数は「クジを当たりが出るまで引く」という試行の結果であり、確率変数である。

3.2

「裏が3枚・表が1枚」の事象が発生した回数は、全体の試行回数が1200回であることから
1200-(75+300+450+75)=300回と計算できる。

「事象と対応する確率」は「事象が発生した回数」をそれぞれ1200で割れば計算できる。
従って、空欄の左から順に,1/4、3/8、1/4、1/16となる。

5.1

「洗濯物を干していた日という条件下で雨が降ってきた日の発生する確率」は、

\begin{align}
P(雨が降ってきた日|洗濯物を干していた日)&=\frac{洗濯物を干していてかつ雨が降ってきた日数}{1年のうち洗濯物を干しっていた日数}\\
&=\frac{12}{60}=\frac{1}{5}
\end{align}

また、「洗濯物を干していてかつ雨が降ってきた日の発生する確率」は,

\begin{align}
P(雨が降ってきた日,洗濯物を干していた日)&=\frac{洗濯物を干していてかつ雨が降ってきた日数}{全ての日数}\\
&=\frac{12}{365}
\end{align}

5.2

5.2.1
赤色は3個で、その中でBと書かれている玉は1つである。

P(B|赤)=\frac{1}{3}

5.2.2

\begin{align}
P(白|A)&=\frac{P(A|白)P(白)}{P(A)}\\
&=\frac{P(A|白)P(白)}{P(A|白)P(白)+P(A|赤)P(赤)}\\
&=\frac{\frac{1}{2}\frac{2}{5}}{\frac{1}{2}\frac{2}{5}+\frac{1}{3}\frac{3}{5}}\\
&=\frac{1}{2}
\end{align}

3. 情報理論

3.1 要約

3.1.1 自己情報量

自己情報量

情報量$w$に対して$\Delta w$増加したとすると、増加率は$\Delta w/ w$となる。
$w$について積分することで、自己情報量が求まる。

I(x)=\log{(W(x))}=-\log{(P(x))}

シャノンエントロピー

自己情報量の期待値

\begin{align}
H(x)&=E(I(x))\\
&=-E(\log{(P(x))})\\
&=-\sum(P(x)\log{(P(x))})
\end{align}

ベルヌーイ分布の場合の例を示す。

3.1.2 カルバック・ライブラー ダイジェンス

カルバック・ライブラー　ダイバージェンス

同じ事象・確率変数における異なる確率分布$P,Q$の違いを示す

D_{KL}(P||Q)=E_{x\sim P}\,\biggr[\log{\frac{P(x)}{Q(x)}}\biggl]=E_{x\sim P}[\log{P(x)}-\log{Q(x)}]

ここで、

I(Q(x))-I(P(x))=(-\log{(Q(x))})-(-\log{(P(x))})=\log{\frac{P(x)}{Q(x)}}

期待値の計算をすると、

D_{KL}(P||Q)=\sum_xP(x)(-\log{(Q(x))})-(-\log{(P(x))})=\sum_xP(x)\log{\frac{P(x)}{Q(x)}}

交差エントロピー

KLダイバージェンスの一部分を取り出したものであり、$Q$についての自己情報量を$P$の分布で平均したもの。

D_{KL}(P||Q)=\sum_xP(x)((-\log{(Q(x))})-(-\log{(P(x))}))

この式は、

H(P,Q)=H(P)+D_{KL}(P||Q)

と変形できる。ここで、

H(P,Q)=-E_{x\sim P}\log{Q(x)}=-\sum_xP(x)\log{Q(x)}

3.2 演習

4.1

4.1.1
1枚の1回投げてコインを投げて表が出る確率は1/2である。

I=\log_2{\frac{1}{2}}=1

1bitとなる。

4.1.2
2枚のコインを1回ずつ投げてすべて表が出る確率は1/4である。

I=\log_2{\frac{1}{4}}=2

2bitとなる。

4.1.3
n枚のコインを1回ずつ投げてすべて表が出る確率は$(1/2)^n$である。

I=\log_2{\bigl(\frac{1}{2}\bigr)^n}=n

n bitとなる。

確認テスト

7.1

\left(\begin{matrix} 
2 \\ 
6 \\
3
\end{matrix}\right)+
\left(\begin{matrix} 
1 \\ 
1 \\
4
\end{matrix}\right)=
\left(\begin{matrix} 
3 \\ 
7 \\
7
\end{matrix}\right)

7.2

固有値、固有ベクトルの定義を利用する。

\left(\begin{matrix} 
1 & 4\\ 
2 & 3
\end{matrix}\right)
\left(\begin{matrix} 
1\\ 
1
\end{matrix}\right)=
\lambda
\left(\begin{matrix} 
1\\ 
1
\end{matrix}\right)\\
\lambda=5

7.3

「ア」である。
7.4

\begin{align}
Var(f)=E((f(x)-E(f(x)))^2)&=E(f(x)^2-2f(x)E(f(x))+E(f(x))^2)\\
&=E(f(x)^2)-E(f(x))^2
\end{align}

7.5

定義より「イ」となる。