「Rによる実証分析」をpythonで書き換えながら読み進めていきます。
章によってはコード部分が少なく説明中心となっている場合もありますがご了承ください。
個人的な勉強が目的の中心となることご理解ください。
前回
回帰分析の基礎
統計的仮説検定の考え方
統計的仮説検定とは
統計的仮説検定とは、「統計学的な背理法」である。
一般な仮説検定の手続きは以下のようになる。
- どれくらい低い確率であれば「現実には起こりえない」と見なすか、その基準を決めておく。この基準を有意水準という。
- ある確率分布について、何らかの仮説を立てる。これを帰無仮説($H_0$)という。また、帰無仮説が否定された場合に採用される、もう1つの仮説を準備する。これを対立仮説($H_1$)という。
- 分布から標本を抽出する。
- 帰無仮説を正しいものとして、3で抽出した標本から得られる確率を計算する。その結果が1で決めた有意水準よりも小さいならば、帰無仮説は真実ではないち結論して棄却し、対立仮説を受容する。確率が有意水準よりも大きいならば、帰無仮説を受容する。
ここで注意することは「帰無仮説が受容」されたからといって「帰無仮説が正しい」というわけではないことである。
回帰分析と統計的仮説検定
回帰分析では、回帰係数の値に関する検定が行われる。
たとえば、「教育年数は賃金の予測に役立つか」という問題を調べたいとする。
このような場合には、以下の手続きに従って分析を行う。
- 賃金を教育年数とその他の説明変数に回帰し、各変数の回帰係数を推定する。
- 回帰分析の推定結果をうまく使って、帰無仮説:$H_0:\beta_{school}=0$を検定する。
- 帰無仮説が棄却されたなら、そのときは対立仮説$H_1:\beta_{school}\neq0$を採用する。帰無仮説が棄却されなかった場合は、仮説$H_0:\beta_{school}=0$を否定できるだけの十分な根拠が得られない。したがって、教育年数の情報が、賃金の予測において役に立たない可能性がある。
平均値の検定
問題設定
ある確率密度関数$f$について、その平均値を$\mu=\int uf(u)du$とする。
いま、この$\mu$の値について「$\mu=0$」または「$\mu\neq0$」の2つの可能性があるものとする。
そして、$f$から無作為に抽出された標本$X_1,\cdots,X_n$を利用することができるとする。
正規分布の場合
母集団の分布が平均$\mu$、標準偏差1の正規分布$N(\mu,1)$であると判明しているケースを考える。
- 有意水準の選択
ここでは、5%とする - 帰無仮説の設定
帰無仮説を$H_0:\mu=0$、対立仮説を$H_1:\mu\neq 0$とする - 標本の抽出
検定の対象となっている母集団$N(\mu,1)$から標本を抽出する。たとえば、大きさ1の標本$X=2.23$だけだ得られたものとする。 - 帰無仮説$H_0:\mu=0$の検定
正規分布に従う確率変数$X$について$|X|<1.96$となる確率は95%、$|X|>1.96$となる確率は5%である。帰無仮説$H_0:\mu=0$のもとで標本$X=2.23$を得る確率は有意水準5%未満であるから、$H_0:\mu=0$は棄却される。
「平均値$\mu$はわからないが、分布が正規分布であることは判明している」という状況は考えづらい。
また、標本の大きさを1とするのも現実的ではない。
t値による方法
そこで問題設定を「母集団分布については何もわからない」とする。
検定の手続きを次のように変える。
- 有意水準を5%とする
- 帰無仮説を$H_0:\mu=0$、対立仮説を$H_1:\mu\neq 0$とする
- 母集団$f$から大きさ$n$の標本を抽出する。$n$が十分に大きな数であれば、中心極限定理により、以下の式で定義される$t$は近似的に正規分布$N(0,1)$に従うものと考えられる。
$$
t=\frac{\sqrt{n}(\bar{X_n}-\mu)}{\sqrt{S_n}}
$$
ただし、$\bar{X_n}$は標本平均、$S_n$は標本分散であり、
$$
\bar{X_n}=\frac{1}{n}\sum_{i=1}^nX_i\
S_n=\frac{1}{n-1}\sum_{i=1}^n(X_i-\bar{X_n})^2
$$
である。 - 帰無仮説$H_0:\mu=0$が正しいものとする。このとき
$$
t=\frac{\sqrt{n}}{\sqrt{S_n}}・\bar{X}_n
$$
は近似的に正規分布$N(0,1)$に従うことになる。特に、$|t|>1.96$であれば、有意水準5%で$H_0:\mu=0$は棄却される。
ここで使用されている統計量$t$を、この検定における$t値$と呼ぶ。
また、t値を用いる検定をt検定と呼ぶ。
有意水準と棄却域
一般に帰無仮説を棄却するか否かを決定する領域を検定の棄却域と呼ぶ。
また、棄却するかどうかを決める基準値1.96を棄却臨界値と呼ぶ。
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib
data = pd.read_csv('R_EmpiricalAnalysis/02 演習用データ集/data_5_1.csv')
print('mean')
print(data.mean())
print('\nvar')
print(data.var())
mean
distA 2.042323
distB 0.074927
dtype: float64
var
distA 0.372785
distB 0.359234
dtype: float64
import numpy as np
import scipy.stats as stats
print('t-value')
t_values = np.sqrt(100) / np.sqrt(data.var()) * data.mean()
print(t_values)
print('p-value')
print(stats.t.sf(t_values, df=n-1)*2)
t-value
distA 33.449949
distB 1.250113
dtype: float64
p-value
[9.27339666e-56 2.14205349e-01]
distAについては有意水準が0.1%であっても、帰無仮説$H_0:\mu=0$は棄却される。
distBについては有意水準が10%であっても帰無仮説は棄却できないことが分かる。
p値による方法
$t=1.25$のときに$H_0:\mu=0$を棄却するためには、有意水準をどこまで大きくする必要があるか、を考えてみる。
つまり、$N(0,1)$に従う確率変数を$Z$とするとき、$|Z|\geq 1.25$となる確率はどれくらいか、ということである。
from scipy.stats import norm
n = len(data)
print('p-value(|Z|>1.25)\n')
print('normal dist: ', norm.sf(1.25,0,1)*2)
print('t dist: ', stats.t.sf(1.25, df=n-1)*2)
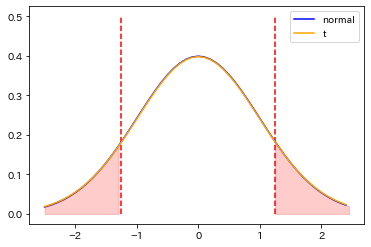
x_all = np.arange(-2.5,2.5,0.1)
x_left = np.arange(-2.5,-1.25, 0.1)
x_right = np.arange(1.25, 2.5, 0.1)
plt.plot(x_all, norm.pdf(x_all, 0, 1), color='blue', label='normal');
plt.plot(x_all, stats.t.pdf(x_all, df=n-1), color='orange', label='t');
plt.vlines([-1.25, 1.25], ymin=0,ymax=0.5, colors='red', linestyles='--')
plt.fill_between(x_left, y1=norm.pdf(x_left, 0, 1), y2=0, alpha=.2, color='red')
plt.fill_between(x_right, y1=norm.pdf(x_right, 0, 1), y2=0, alpha=.2, color='red')
plt.legend();
p-value(|Z|>1.25)
normal dist: 0.2112995473337107
t dist: 0.21424633756838654
およそ21%となることがわかる。この確率を当該検定におけるp値という。
したがって、分布Bについて帰無仮説$H_0:\mu=0$を棄却したいのであれば、21%の有意水準を認めるほかない。
$t$ 検定では事前に決められた有意水準に対応する棄却臨界値を求める必要がある。
$p$値に基づく方法は、得られた値より極端な値が出る確率を計算して判定を行うことから、
$t$値(棄却臨界値)との大小による判定に比べて精密な検定方法であるといえる。
回帰係数の検定
OLS推定量の漸近分布
単回帰分析について考える。
単回帰モデル
$$
\left\{
\begin{array}{ll}
y=\beta_0+\beta_1x+\varepsilon \\
E(y|x)=\beta_0+\beta_1x
\end{array}
\right.
$$
を仮定する。
標本${(y_i,x_i):i=1,\cdots,n }$が得られたとき、回帰係数$\beta_1$のOLS推定量は
$$
\hat{\beta_1}=\frac{\sum_{i=1}^n(x_i-\bar{x_n})(y_i-\bar{y_n})}{\sum_{i=1}^n(x_i-\bar{x_n})^2}
$$
によって計算される。中心極限定理を適用することで、標本平均と同様に、$\hat{\beta}_1$についても十分大きな$n$のもとで、
$$
Z_n=\frac{\sqrt{n}(\hat{\beta}_1-\beta_1)}{\sqrt{S_n}}
$$
が近似的に正規分布$N(0,1)$に従うことを示せる。
ここで$S_n$は標本分散である。
式を以下のように変形する。
$$
\hat{\beta}_1=\beta_1+\frac{\sqrt{S_n}}{\sqrt{n}}Z_n
$$
十分に大きな$n$で$Z_n$は近似的に$N(0,1)$に従うから、$\sigma=\frac{\sqrt{S_n}}{\sqrt{n}}$と書けば、$\hat{\beta}_1$は平均$\beta_1$、標準偏差$\sigma$の正規分布$N(\beta_1,\sigma^2)$に従うことになる。
この$N(\beta_1,\sigma^2)$をOLS推定量$\hat{\beta}_1$の漸近分布という。ある推定量の漸近分布の標準偏差$\sigma$を標準誤差という。
from sklearn.linear_model import LinearRegression
S = 10000 # 繰り返し回数
beta1 = np.zeros(S)
for i in range(S):
x = np.random.randn(1000)+0.1
y = 1+5*x+np.random.randn(1000)+0.1
lm = LinearRegression()
lm.fit(x.reshape(-1, 1), y)
beta1[i] = lm.coef_[0]
pd.DataFrame(beta1).describe().T
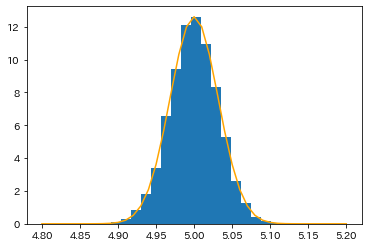
plt.hist(beta1, bins=20, density=True);
plt.plot(np.arange(4.8,5.2,0.01), norm.pdf(np.arange(4.8,5.2,0.01), 5, 0.031627), color='orange');
10000個の推定値は、$\beta_1=5$を中心として左右対称に分布していることがわかる。
また、$\hat{\beta}_1$の標準偏差はおよそ$\sigma=0.032$であるので、漸近分布はおおむね$N(5,(0.032)^2)$となる。
回帰係数のt検定
もし$\beta_1=0$であるならば、$\hat{\beta}_1$の漸近分布は$N(0,\sigma^2)$となる。さらに、
$$
t=\frac{\hat{\beta}_1}{\sigma}
$$
によって$\hat{\beta}_1$の$t$値を定義すれば、これは正規分布$N(0,1)$に従う。
帰無仮説の下で$|t|>1.96$となる確率は5%以下のはずだから、もし$|t|>1.96$となれば有意水準5%で帰無仮説を棄却できる。
回帰係数のt検定の手順
- 単回帰モデル$y=\beta_0+\beta_1x+\varepsilon$の係数$\beta_1$について、帰無仮説を$H_0:\beta_1=0$、対立仮説$H_1:\beta_1\neq0$とする
- OLS推定量$\hat{\beta}_1$と、標準誤差$\sigma$を計算する
- $t=\hat{\beta}_1\ /\ \sigma$として、$|t|>1.96$であれば、有意水準5%で帰無仮説$H_0:\beta_1=0$を棄却する
p値による回帰係数の検定
p値による回帰係数の検定の手順
- 単回帰モデル$y=\beta_0+\beta_1x+\varepsilon$の係数$\beta_1$について、帰無仮説を$H_0:\beta_1=0$、対立仮説$H_1:\beta_1\neq0$とする
- OLS推定量$\hat{\beta}_1$と、標準誤差$\sigma$を計算する
- $t=\hat{\beta}_1\ /\ \sigma$の値を計算する
- $N(0,1)$に従う確率変数$Z$について、$|Z|>|t|$となる確率を計算する。この値が小さいほど、帰無仮説を棄却することが容易であると考える。
重回帰分析の場合
重回帰モデル
$$
\left\{
\begin{array}{ll}
y=\beta_0+\beta_1x_1+\beta_2x_2++\cdots+\beta_dx_d+\varepsilon \\
E(y|x)=\beta_0+\beta_1x_1+\beta_2x_2++\cdots+\beta_dx_d
\end{array}
\right.
$$
の場合でも、検定については単回帰と変わらない。
帰無仮説$H_0:\beta_k=0$のもとで、
$$
t_k=\frac{\sqrt{n}}{\sqrt{s_k}}\hat{\beta}_k
$$
が$N(0,1)$に従う。ここで、$s_k$は標本に基づいて計算される値である。
もし、$|t_k|>1.96$であれば、融資水準5%のもとで$H_0:\beta_k=0$が棄却される。
data = pd.read_csv('R_EmpiricalAnalysis/02 演習用データ集/data_Males.csv')
data.head()
import statsmodels.api as sm
df_X = sm.add_constant(data[['school','exper']])
df_y = data['wage']
model = sm.OLS(df_y, df_X)
result = model.fit()
print(result.summary())
OLS Regression Results
==============================================================================
Dep. Variable: wage R-squared: 0.083
Model: OLS Adj. R-squared: 0.079
Method: Least Squares F-statistic: 24.42
Date: Sun, 27 Mar 2022 Prob (F-statistic): 7.01e-11
Time: 10:00:33 Log-Likelihood: -430.87
No. Observations: 545 AIC: 867.7
Df Residuals: 542 BIC: 880.6
Df Model: 2
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const -0.1611 0.224 -0.718 0.473 -0.602 0.280
school 0.1085 0.016 6.734 0.000 0.077 0.140
exper 0.0923 0.017 5.427 0.000 0.059 0.126
==============================================================================
Omnibus: 173.831 Durbin-Watson: 2.037
Prob(Omnibus): 0.000 Jarque-Bera (JB): 608.476
Skew: -1.461 Prob(JB): 7.43e-133
Kurtosis: 7.272 Cond. No. 121.
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
たとえばschoolの回帰係数$\hat{\beta_{school}}$は、真の回帰係数$\beta_{school}$を中心とする正規分布$N(\beta_{school},(0.016)^2)$に従っているものとみなせる。また、$\hat{\beta_{exper}}$の漸近分布は$N(\beta_{exper},(0.017)^2)$と考えられる。
帰無仮説$H_0:\beta_{school}$に対するt値は、 $t=\hat{\beta_{exper}}\ /\ \sigma_{school}$となっている。
t_value = 0.1085 / 0.016
print('t-value: ', t_value)
p_value = stats.t.sf(t_value, df=n-1)*2
print('p-value: ', p_value)
t-value: 6.78125
p-value: 8.748991505782372e-10
この回帰において、schoolとexperは有意な変数といえる。
信頼区間
回帰係数の信頼区間
回帰係数の推定量$\hat{\beta}=(\hat{\beta}_0,\hat{\beta}_1,\cdots,\hat{\beta}_d)$の各要素$\hat{\beta}_k(k=0,1,\cdots,d)$について信頼区間を構成することを考える。
たとえば$\hat{\beta}_k$の漸近分布が$N(\hat{\beta}_k,\sigma^2_k)$であるとする。$n$が十分大きいときには、
$$
Z_k=\frac{\hat{\beta}_k-\beta_k}{\sigma_k}
$$
は$N(0,1)$に従うものと見なせるとする。
よって十分に大きな$n$のもとでは、
$$
P(|Z_k|<1.96)=P\biggl(-1.96\leq \frac{\hat{\beta}_k-\beta_k}{\sigma_k}\leq 1.96 \biggr)=0.95
$$
と近似できるはずである。
これにより、$\beta_k$の95%信頼区間は
$$
\hat{\beta}_k-1.96\sigma_k\leq \beta_k\leq \hat{\beta}+1.96\sigma_k
$$
となる。
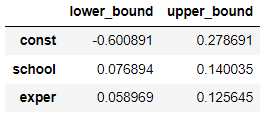
CI = pd.DataFrame({'lower_bound':result.params - 1.96 * result.bse,
'upper_bound':result.params + 1.96 * result.bse})
CI
$\beta_{school}$の信頼区間はおよそ0.08~0.14、$\beta_{exper}$の信頼区間はおよそ0.06~0.12であることがわかる。
$t$検定ではわからなかった推定精度の評価が可能となった。
次回
相関関係と因果関係
参考文献