pythonで「データ解析のための統計モデリング入門」1 確率分布と統計モデリングの最尤推定

「データ解析のための統計モデリング入門」はRで書かれた本ですが、これをpythonで書き直しながら読み進めていきます。
内容の理解と読み進めることが目的ですので、ベストなコードではないことをご理解ください。
たくさんの人がやっているような内容だとは思いますが、ご了承ください。

1. 確率分布と統計モデリングの最尤推定

1.1 例題:種子数の統計モデリング

植物50体からなる集団を調査していて、各個体の種子数を数えたデータがあるとする。
このデータはカウントデータであり、非負の整数である。

import numpy as np

data = np.loadtxt('rdata1.txt')

data

array([2., 2., 4., 6., 4., 5., 2., 3., 1., 2., 0., 4., 3., 3., 3., 3., 4.,
       2., 7., 2., 4., 3., 3., 3., 4., 3., 7., 5., 3., 1., 7., 6., 4., 6.,
       5., 2., 4., 7., 2., 2., 6., 2., 4., 5., 4., 5., 1., 3., 2., 3.])

データの個数を確認する。

len(data)

50

標本平均や標準偏差などの統計量を確認する。

import pandas as pd

pd.DataFrame(pd.Series(data.ravel()).describe()).transpose()

度数分布の確認。

np.histogram(data, bins=8)

(array([ 1,  3, 11, 12, 10,  5,  4,  4], dtype=int64),
array([0.   , 0.875, 1.75 , 2.625, 3.5  , 4.375, 5.25 , 6.125, 7.   ]))

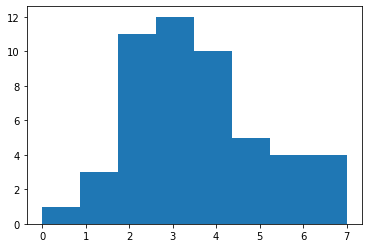
ヒストグラムの表示

import matplotlib.pyplot as plt

plt.hist(data, bins=8)

データのばらつきを表す統計量として、標本分散がある。

np.var(data, ddof=1)

2.986122448979592

標本標準偏差は標本分散の平方根となる。

print(np.std(data, ddof=1))
print(np.sqrt(np.var(data, ddof=1)))

1.728040060004279
1.728040060004279

1.2 データと確率分布の対応関係を眺める

植物の種子数データは

• 1個、2個と数えるカウントデータ
• 1個体の標本平均は3.56個
• 個体ごとに種子数にばらつきがあり、ヒストグラムではひと山の分布

という特徴があることが分かった。
とりあえずポアソン分布と呼ばれる確率分布で表現することを考える。
確率分布とは、確率変数の値とそれが出現する確率を対応させたものである。
確率分布は比較的簡単な数式で定義され、パラメータの値に依存して分布の形が変わる。

ここで、「平均3.56のポアソン分布」を考える。
「平均3.56のポアソン分布」に従って「種子数がyであると観測される確率」を生成させる。

from scipy.stats import poisson

y = np.arange(0,10)
prob = poisson.pmf(y, mu=3.56)

plt.plot(y, prob, '--o')

print(y.T, '\n', prob)

[0 1 2 3 4 5 6 7 8 9] 
 [0.02843882 0.10124222 0.18021114 0.21385056 0.190327   0.13551282
 0.08040427 0.04089132 0.01819664 0.00719778]

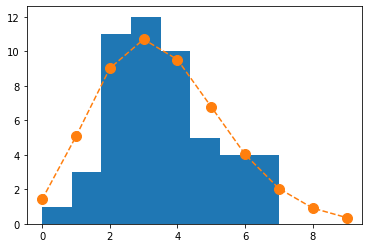
観測データのヒストグラムに平均3.56のポアソン分布を重ねると、
観測されたばらつきはポアソン分布で表現されそうと予測できる。

plt.hist(data, bins=8)
plt.plot(y, prob*50, '--o',markersize=10)

1.3 ポアソン分布

ポアソン分布は次の数式で定義される。
$$
p(y|\lambda)=\frac{\lambda^y\exp{(-\lambda)}}{y!}
$$
この式は、平均が$\lambda$のときに、ポアソン分布にしたがう確率変数が$y$という値になる確率である。
ポアソン分布の性質を挙げる。

• $y\in{0,1,2,\cdots,\infty}$の値をとり、すべての$y$について和をとると1になる
  $$
  \sum_{y=0}^{\infty}p(y|\lambda)=1
  $$
• 確率分布の平均は$\lambda$である($\lambda \geqq 0$)
• 分散と平均は等しい:$\lambda$=平均=分散

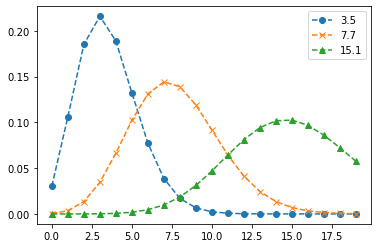
ここで、ポアソン分布のパラメータ$\lambda$を変化させると、確率分布は図のように変化する。

y = np.arange(0,20)

plt.plot(y, poisson.pmf(y, mu=3.5), '--o', label='3.5')
plt.plot(y, poisson.pmf(y, mu=7.7), '--x', label='7.7')
plt.plot(y, poisson.pmf(y, mu=15.1), '--^', label='15.1')
plt.legend()

なぜポアソン分布が選ばれたのか、その理由としては下のようなものが挙げられる。

1. データに含まれている値$y_i$が${0,1,2,\cdots}$といった非負の整数である(カウントデータである)
2. $y_i$に下限(ゼロ)はあるが、上限については不明
3. この観測データでは平均と分散がだいたい等しい

その他にもいくつか前提が必要であるが、それらは成立しているとここでは考える。

1.4 ポアソン分布のパラメータの最尤推定

確率分布のパラメータを、観測データに基づいて推定する方法を考える。
最尤推定法は尤度という「あてはまりの良さ」を表す統計量を最大にするパラメータ推定方法である。
尤度の実態は、ある$\lambda$の値を決めた時の、すべての個体$i$についての$p(y_i|\lambda)$の積である。
たとえば、データが3個分${y_1,y_2,y_3}={2,2,4}$だった場合、
尤度はだいたい$0.180×0.180×0.190=0.006156$といった値になる。

尤度はパラメータの関数であるので$L(\lambda)$と書き、この例題では次のように定義される。
$$
\begin{align}
L(\lambda)&=(y_1が2である確率)×(y_2が2である確率)×\cdots×(y_{50}が3である確率)\\
&=p(y_1|\lambda)×p(y_2|\lambda)×p(y_3|\lambda)×\cdots×p(y_{50}|\lambda)\\
&=\prod_{i}p(y_i|\lambda)\\
&=\prod_{i}\frac{\lambda^{y_i}\exp{(-\lambda)}}{y_i!}
\end{align}
$$
対数尤度関数は、
$$
\log{L(\lambda)}=\sum_i\biggl(y_i\log{\lambda}-\lambda-\sum_{k}^{y_i}\log{k}\biggr)
$$

fig = plt.figure(figsize=(16,12))
x = np.arange(8)
mu = np.arange(2.0, 5.6, 0.4)

calc_logL = lambda x, mu: np.sum(np.log(poisson.pmf(x, mu=mu)))

for i in range(9):
    logL = np.round(calc_logL(data, mu[i]), decimals=1)
    prob = poisson.pmf(x, mu=mu[i])
    label = 'lambda={}\nlogL={}'.format(np.round(mu[i], decimals=1), logL)
    
    ax = fig.add_subplot(3, 3, i+1)
    ax.hist(data, bins=8)
    ax.plot(x, prob*50, '--o',markersize=10, label=label)
    ax.legend()

対数尤度と$\lambda$の関係を調べる。

lmd = np.arange(2, 5, 0.01)

logL = np.array([calc_logL(data, l) for l in lmd])
max_idx = np.argmax(logL)

print('max logL :', logL[max_idx])
print('lambda_hat :', lmd[max_idx])

plt.plot(lmd, logL);
plt.xlabel('lambda');
plt.ylabel('logL');

max logL : -97.24400294080664
lambda_hat : 3.5599999999999667

対数尤度が最大になる$\lambda$を$\hat{\lambda}$とする。
対数尤度関数が最大値で関数の傾きがゼロとなる$\lambda$を探しだせばよい。

$$
\frac{\partial \log{L(\lambda)}}{\partial \lambda}=\sum_i\biggl\{\frac{y_i}{\lambda}-1 \biggr\}=\frac{1}{\lambda}\sum_iy_i-50
$$

これがゼロである場合、
$$
\hat{\lambda}=\frac{1}{50}\sum_iy_i=\frac{全部のy_iの和}{データ数}=データの標本平均=3.56
$$
となる。
最尤推定値$\hat{\lambda}$は3.56であり、標本平均に等しくなる。
このように対数尤度または尤度が最大になる$\hat{\lambda}$を最尤推定量 、
具体的な$y_i$の値を使って評価された$\hat{\lambda}=3.56$のことを最尤推定値と呼ぶ。

一般化すると、$\theta$をパラメータとする確率分布から観測データ$y_i$が発生した場合、その確率を$p(y|\theta)$とすると、尤度は、
$$
L(\theta|\boldsymbol{Y})=\prod_ip(y_i|\theta)
$$
対数尤度は、
$$
\log{L(\theta|\boldsymbol{Y})}=\sum_i\log{p(y_i|\theta)}
$$
であり、最尤推定はこの対数尤度を最大にするような$\hat{\theta}$を探すことである。

2.5 統計モデルの要点

データが与えられたとき、「こういうばらつきのあるデータは、何か確率分布から発生した」と考える。
データを発生させた統計モデルが「真の統計モデル」であり、これが平均3.56のポアソン分布であるとしている。
観測データを見たときに「ポアソン分布で説明できる」と仮定したときに、「パラメータ$\lambda$の値は？」という問いに答えるのが推定である。
また、予測とは、次のデータの分布を見積もることである。

• 次に得られる応答変数の平均だけを示す
• 平均だけでなく、次に得られるデータの範囲の予測区間を示す

1.6 確率分布の選び方

データを見たら以下の点に気を付ける。

• 説明したい量は離散か連続か？
• 説明したい量の範囲は？
• 説明したい量の標本分散と標本平均の関係は？

ここでは、カウントデータの統計モデルで使う確率分布として

• ポアソン分布：データが離散値、ゼロ以上、上限なし、平均$\approx$分散
• 二項分布：データが離散値、ゼロ以上で有限の範囲、分散は平均の関数
  を使用する。

また、連続確率分布では、

• 正規分布：データが連続値、範囲が$[-\infty,\infty]$、分散は平均とは無関係
• ガンマ分布：データが連続値、範囲が$[0,\infty]$、分散は平均の関数

などがある。

次回

一般化線形モデル(GLM)

参考書