pythonによるネットワーク分析のメモ書きとなります。
networkxを使用します。
内容・コードがまとまっていないので、詳細については参考書の参照をお願いします。
機会があればしっかり勉強していこうと思います。
中心の定義
中心性には以下のような様々な定義がある。
- 他の多くの頂点とつながっている頂点
- その頂点が欠けるとグラフがばらばらになるような頂点
- 多くの経路上に現れる頂点
- 他の頂点に短い距離で到達できる頂点
次数中心性
多くの頂点と隣接している頂点は中心的とするものであり、頂点$v$の次数中心性は、その時数$k_v$で表される。
グラフ$G=(V,E)$の頂点数を$|V|=n$としたとき、すべての頂点の次数を表す次数ベクトル$k$は、隣接行列$A$と、各要素が1である列ベクトル$\boldsymbol{1}$を用いて、$k=A・\boldsymbol{1}$
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
import networkx as nx
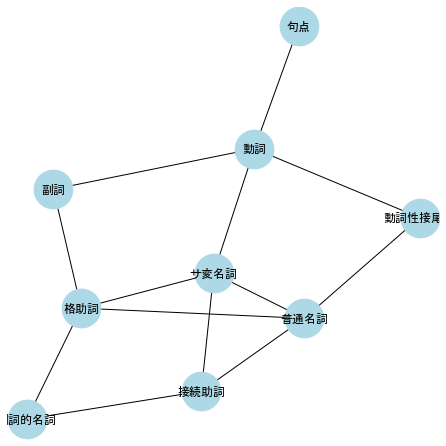
d = pd.read_csv('pos.csv', encoding='shift-jis')
# Graphオブジェクトの作成
G = nx.Graph()
G.add_nodes_from(np.unique([d.形態素1]+[d.形態素2]))
G.add_edges_from([(d.loc[i, '形態素1'], d.loc[i, '形態素2']) for i in range(len(d))])
# ネットワークの可視化
plt.figure(figsize=(6,6))
nx.draw(G, node_size=1500, node_color='lightblue', with_labels=True, font_family='MS Gothic')
print('degree centrality:')
for k, v in sorted(nx.degree_centrality(G).items(), key=lambda x: -x[1]):
print(str(k)+":"+"{:.3f}".format(v)+" ", end="")
degree centrality:
サ変名詞:0.500 動詞:0.500 動詞性接尾辞:0.500 普通名詞:0.500 格助詞:0.500 接続助詞:0.375 副詞:0.250 副詞的名詞:0.250 句点:0.125
固有ベクトル中心性
隣接する頂点の中心性も加味し、「他の中心的な頂点と隣接する頂点は中心的」とするものである。
周囲の頂点の中心性$x_i$から計算される$x_i'$は
x_i'=\sum_iA_{ij}x_j
であり、列ベクトルと行列の積で表すと
\boldsymbol{x}'=A\boldsymbol{x}
となる。
このような反復計算を繰り返すと、列ベクトルは最終的に$A$の最大固有値に対応する固有ベクトルに収束する。
得られた列ベクトルの$i$番目の成分が頂点$i$の固有ベクトル中心性である。
print('eigenvector centrality')
for k, v in sorted(nx.eigenvector_centrality(G).items(), key=lambda x: -x[1]):
print(str(k)+":"+"{:.3f}".format(v)+" ", end="")
eigenvector centrality
普通名詞:0.452 サ変名詞:0.451 格助詞:0.399 接続助詞:0.335 動詞性接尾辞:0.331 動詞:0.327 副詞的名詞:0.219 副詞:0.217 句点:0.097
Katz中心性
固有ベクトル中心性において、辺に向きがある有向グラフの場合に、他のどの頂点からも辺が入ってこない頂点は、中心性が0となります。
さらに、そのような頂点からしか辺が入ってこない頂点の中心性も0になってしまう問題がある。
Katz中心性は「固有ベクトル中心性に加えて、すべての頂点に一定量の中心性を与えたもの」である。
x_i=\sum_iA_{ij}x_j+\beta
PageRank
Katz中心性は、中心性の高い頂点が1つあると、それに隣接する頂点の中心性もすべて高くなってしまう。
そこで、頂点$i$の中心性を計算する際に、隣接する頂点$j$の中心性を、その頂点の次数$k_i$で割ったものを足すこととする。
x_i=\sum_iA_{ij}\frac{x_j}{k_j}+\beta
媒介中心性
「2頂点間を結ぶ経路上にしばしば現れる頂点を中心的」とする考え方。
$n_{st}^i$を頂点$s$と$t$を結ぶパスが頂点$i$を通るときに1、そうでないときに0となるとしたとき、頂点$i$の媒介中心性は
x_i=\sum_{st}n_{st}^i
と表せる。次数が小さい頂点であっても、媒介中心性が大きい場合がある。
print('betweenness centrality')
for k, v in sorted(nx.betweenness_centrality(G).items(), key=lambda x: -x[1]):
print(str(k)+":"+"{:.3f}".format(v)+" ", end="")
betweenness centrality
動詞:0.330 サ変名詞:0.220 格助詞:0.217 普通名詞:0.146 接続助詞:0.077 副詞:0.060 動詞性接尾辞:0.036 副詞的名詞:0.021 句点:0.000
近接中心性
「ネットワークの他の頂点との平均距離が短い頂点を中心的」とするもの。
頂点$i$と頂点$j$の間の距離を$d_{ij}$とすると、$l_i=\frac{1}{n}\sum_jd_{ij}$が頂点$i$の中心性である。
値が小さいものの方がより中心的となる。
print('closeness centrality')
for k, v in sorted(nx.closeness_centrality(G).items(), key=lambda x: -x[1]):
print(str(k)+":"+"{:.3f}".format(v)+" ", end="")
closeness centrality
サ変名詞:0.667 動詞:0.615 普通名詞:0.615 格助詞:0.615 副詞:0.533 動詞性接尾辞:0.533 接続助詞:0.533 副詞的名詞:0.444 句点:0.400
参考文献