pythonで「入門 機械学習による異常検知」を読む2 非正規データからの異常検知

「入門 機械学習による異常検知」はRで書かれた異常検知の本です。
今回は実装部分をpythonで書き直していこうと思います。

個人的な勉強のメモ書きとなります。
1章当たりのボリュームが多く、数式もかなりあるためうまくまとまっていません。
また、schikit-learnなどで関数が提供されていれば使っています。
導出や詳細などは「入門 機械学習による異常検知」を読んでいただければと思います。

前回

正規分布に従うデータからの異常検知

1. 分布が左右対称でない場合

ひと山であるが、
1. 正の値しかとらない
2. 分布が左右対称ではない

という特徴を持つデータに対しては、カイ二乗分布、またはその別表現であるガンマ分布のあてはめが有効である。

$$
g(x|k,s)=\frac{1}{s\Gamma (k)}\biggl(\frac{x}{s} \biggr)^{k-1}\exp\biggl(-\frac{x}{s} \biggr)
$$

この式から$g(x|k/2,2s)=\chi^2(x|k,s)$であることがわかる。
また、$\Gamma (k)=(k-1)!$である。

対数尤度からの計算は難しいためモーメント法という手法を用いる。
1次と2次のモーメントは、データから

<x>=\frac{1}{N}\sum_{n=1}^Nx^{(n)}\\
<x^2>=\frac{1}{N}\sum_{n=1}^Nx^{(n)2}

と計算できる。
$\hat{\mu}=<x>$ および$\hat{\sigma}^2=<x^2>-\hat{\mu}^2$ と書けるから、
モーメント法による推定量$\hat{k}_{mo}$と$\hat{s}_{mo}$ 次のように表せる。

\hat{k}_{mo}=\frac{<x>^2}{<x^2>-<x>^2}=\frac{\hat{\mu}^2}{\hat{\sigma}^2}\\
\hat{s}_{mo}=\frac{<x^2>-<x>^2}{<x>}=\frac{\hat{\sigma}^2}{\hat{\mu}}

異常度の定義は、負の対数尤度$-\ln g(x'|\hat{k}_m,\hat{s}_m)$から$x'$に依存しない項を省略して次のようにする。
$$
a(x')=\frac{x'}{\hat{s}_m}-(\hat{k}_m-1)\ln \frac{x'}{\hat{s}_m}
$$
閾値の設定については、異常度の確率分布を求めることが簡単でないので、分位点を使用する。

手順(ガンマ分布による異常検知)
1. ステップ1(分位推定)　モーメント法、あるいは数値最適化におｙる最尤法によって、ガンマ分布にパラメータを推定する。
2. ステップ2(異常度の定義)　新たな観測値$x'$を得るたびに、異常度$a(x')$を計算する。
3. ステップ3(閾値の設定)　訓練データを使ってあらかじめ$\alpha$パーセンタイルに対応する異常度の値$a_{th}(\alpha)$を求めておき、$a(x')>a_{th}(\alpha)$なら警報発報

import pandas as pd
import numpy as np
from scipy.stats import gamma
import matplotlib.pyplot as plt

x = davis['weight']

# 平均と標準偏差の計算
N = len(x)
mu = np.mean(x)
si = np.std(x)

# kとsの最尤推定値の計算
kmo = (mu/si)**2
smo = si**2/mu

# 異常度の計算
a = davis['weight'] / smo - (kmo - 1)*np.log(davis['weight']/smo)

# パーセンタイルで閾値の設定
ath = np.sort(a)[-int(N*0.01)]

plt.scatter(np.arange(len(x)), a, color = ['red' if a > ath else 'blue' for a in a]);
plt.hlines(ath, xmin=0, xmax=200, linestyles='--', color='red');

2. 訓練データに異常標本が混ざっている場合

観測データ$D= { x^{(n)}|n=1,\cdots,N }$　が得られているとする。
ここで、$D$が背景雑音によって汚染されていると考える。

山を表現するのに正規分布を使ったとすると、式の上では次のようになる。

p(x)=\pi_0N(x|\mu_0,\sigma_0^2)+\pi_1N(x|\mu_1,\sigma_1^2)

ここで、添字の0は正常標本、1が異常標本を表している。
そいて$\pi_0$が正常標本が観測される確率、$\pi_1$が異常標本が観測される確率を表す。
$x$についての規格化条件から、

1=\int_0^\infty dxp(x)=\pi_0+\pi_1

が成り立つ必要がある。
このような正規分布の一次結合で表される分布を、混合正規分布または混合ガウス分布と呼ぶ。
このモデルのパラメータをまとめて、
$$
\boldsymbol{\theta}=(\pi_0,\mu_0,\sigma_0^2,\pi_1,\mu_1,\sigma_1^2)^T
$$
のようにベクトルで表す。
対数尤度$L(\boldsymbol{\theta}|D)$は、

L(\boldsymbol{\theta}|D)=\sum_{n=1}^N\ln\bigl\{\pi_0N(x|\mu_0,\sigma_0^2)+\pi_1N(x|\mu_1,\sigma_1^2) \bigr\}

である。
これは、期待値-最大化(EM)法という技術で、パラメータ推定公式を導くことができる。

手順(1次元混合正規分布の期待値-最大化法)
K成分混合正規分布モデル
$$
p(x)=\pi_1N(x|\mu_1,\sigma_1^2)+\cdots+\pi_KN(x|\mu_K,\sigma_K^2)
$$
のパラメータ${\pi_i,\mu_i,\sigma_i^2}(i=1,2,\cdots,K)$を求めるための手順は次の通り。
1. パラメータ${\pi_i,\mu_i,\sigma_i^2}(i=1,2,\cdots,K)$の初期値を適当に与える
2. ${\pi_i,\mu_i,\sigma_i^2}(i=1,2,\cdots,K)$の値を基に、
$$
q_i^{(n)}=\frac{\pi_iN(x|\mu_i,\sigma_i^2)}{\sum_{l=1}^K\pi_lN(x|\mu_l,\sigma_l^2)}
$$
より、データ$x^{(n)}$の山$i$への帰属度$q_i^{(n)}$を求める
3. ${q_i^{(n)}}$の値を基に、

\hat{\mu}_i=\frac{\sum_{n=1}^Nq_i^{(n)}x^{(n)}}{\sum_{n'=1}^Nq_i^{(n')}}\\
\hat{\sigma}_i^2=\frac{\sum_{n=1}^Nq_i^{(n)}(x^{(n)}-\hat{\mu}_i)^2}{\sum_{n'=1}^Nq_i^{(n')}}\\
\hat{\pi}_i=\frac{1}{N}\sum_{n=1}^Nq_i^{(n)}

を計算する
4. 値が収束していなければ2に戻る

以下の疑似的なデータでEM法を実装して確認する。

import numpy as np
from scipy.stats import norm

# データ数
N = 1000

# 混合させる分布のパラメータ
pi0 = 0.6
pi1 = 0.4
mu0 = 3
sig0 = 0.5
mu1 = 0
sig1 = 3

# 0,1を適当に振り分ける
attr = np.random.choice(a=[0, 1], size=N, p=[pi0, pi1])

# データを格納
x = np.array([-99.]*N)
x[attr==0] = norm.rvs(loc=mu0, scale=sig0, size=np.sum(attr==0))
x[attr==1] = norm.rvs(loc=mu1, scale=sig1, size=np.sum(attr==1))

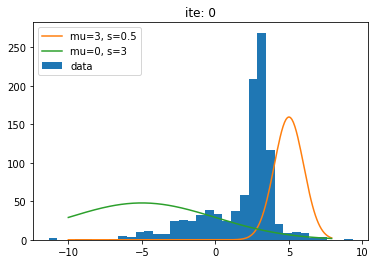
_x = np.arange(-10,8,0.1)

plt.hist(x, bins=35, label='data');
plt.plot(_x, norm.pdf(_x, loc=mu0, scale=sig0)*400, label='mu=3, s=0.5')
plt.plot(_x, norm.pdf(_x, loc=mu1, scale=sig1)*600, label='mu=0, s=3')
plt.legend();

判定結果が変化しなくなるまで更新を繰り返す。

# 初期値の設定
pi0 = 0.5
pi1 = 0.5

mu0 = 5
mu1 = -5

sig0 = 1
sig1 = 5

# 判定結果を格納させる
j = [False]*len(x)

for i in np.arange(100):
    plt.hist(x, bins=35, label='data');
    plt.plot(_x, norm.pdf(_x, loc=mu0, scale=sig0)*400, label='mu=3, s=0.5')
    plt.plot(_x, norm.pdf(_x, loc=mu1, scale=sig1)*600, label='mu=0, s=3')
    plt.legend();
    plt.title('ite: ' + str(i))
    plt.show()

    piN0 = pi0 * norm.pdf(x, loc=mu0, scale=sig0)
    piN1 = pi1 * norm.pdf(x, loc=mu1, scale=sig1)

    # 帰属度の計算
    qn0 = piN0 / (piN0 + piN1)
    qn1 = piN1 / (piN0 + piN1)

    # πの更新
    pi0 = np.sum(qn0)/N
    pi1 = np.sum(qn1)/N

    # μの更新
    mu0 = np.sum(qn0*x)/(N*pi0)
    mu1 = np.sum(qn1*x)/(N*pi1)

    # σの更新
    sig0 = np.sqrt(np.sum(qn0*(x-mu0)*(x-mu0)) / (N*pi0))
    sig1 = np.sqrt(np.sum(qn1*(x-mu1)*(x-mu1)) / (N*pi1))

    # 判定が変わらなければ終了
    if np.all(j == (qn0>qn1)):
        print('break', i)
        break

    j = qn0>qn1

print('pi0, pi1: ', pi0, pi1)
print('mu0, mu1: ', mu0, mu1)
print('sig0, sig1: ', sig0, sig1)

最終的な値は最初に設定したものに近い値が得られた。
学習の様子をグラフにしたものを示す。
更新を繰り返すごとに本来の分布に近づいていることがわかる。

3. 分布がひと山にならない場合：近傍距離に基づく方法

手順(近傍法による異常検知)　異常が含まれないと信じられるデータセット$D$を用意する。標本間の距離尺度を決める(通常、ユークリッド距離かマハラノビス距離)

(1)k基準　なんらかの方法で適切な$\epsilon$を決める。また、近傍数の閾値$k_{th}$を与える
　1. 新たな観測値$\boldsymbol{x'}$に対して、半径$\epsilon$の範囲に入る標本を$D$から選ぶ
　2. その標本の数$k$が閾値$k_{th}$を下回ったら$\boldsymbol{x'}$は異常

(2)$\epsilon$基準　なんらかの方法で適切な$k$を決める。また、近傍数の閾値$\epsilon_{th}$を与える
　1. 新たな観測値$\boldsymbol{x'}$に対して、$k$近傍となる標本を$D$から選ぶ
　2. それらを取り囲む最小の半径$\epsilon$を求める。それが$\epsilon_{th}$を上回ったら$\boldsymbol{x'}$は異常

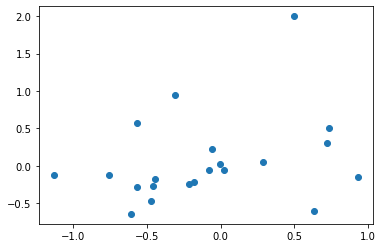
以下のデータで動作を確認する。

x1, y1 = norm.rvs(loc=0, scale=0.5, size=20), norm.rvs(loc=0, scale=0.5, size=20)

X = np.concatenate([
np.array(list(x1)+[0.5]).reshape(-1,1),
np.array(list(y1)+[2]).reshape(-1,1)
], axis=1)

plt.scatter(X[:,0], X[:,1])

schikit-learnのNearestNeighborsで近傍点の距離が計算できるので、
これを利用してk基準、$\epsilon$基準で異常判定を行う。

from sklearn.neighbors import NearestNeighbors

# 半径
k_thresh = 1

# 近傍点の算出
d_neigh = NearestNeighbors(n_neighbors=5)
d_neigh.fit(X)
d = neigh.kneighbors(X)[0]

# 半径k_thresh内の点の数
r = [np.sum(np.array(i)<k_thresh) for i in d]

# 𝜖基準
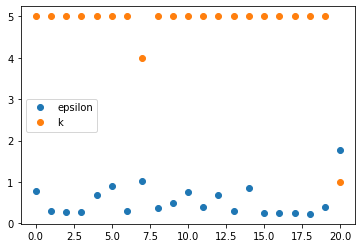
plt.plot(d.max(axis=1), 'o', label='epsilon')

# k基準
plt.plot(r, 'o', label='k')
plt.legend();

どちらの基準においても20番目のデータ点が異常であると判定された。
これは散布図における右上のデータである。

この手法は一様なデータに対して適用されるものである。

局所外れ値度

下の図には2つのクラスターがあるが、密集度に大きな違いがある。
素朴な近傍距離の考え方からすると、赤い星ではなく緑の星を異常と判断してしまう。
そちらのほうが疎な領域にあるためである。

x1, y1 = norm.rvs(loc=0, scale=0.5, size=20), norm.rvs(loc=0, scale=0.5, size=20)
x2, y2 = norm.rvs(loc=6, scale=2, size=20), norm.rvs(loc=6, scale=2, size=20)

plt.plot(x1,y1,'o')
plt.plot(x2,y2,'o')

plt.plot(0.5, 2, marker='*', color='red', markersize=10)
plt.text(0.8, 2, 'p', color='red')

plt.plot(5, 5, marker='*', color='green', markersize=10)
plt.text(5.3, 5, 'q', color='green')

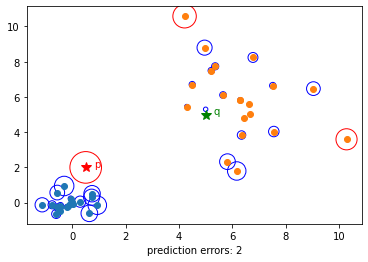
この問題を解決するた目の簡単な方法は、着目点を中心にした近傍に加えて、比較される相手方の近傍距離も考えることである。
着目点を図の通り$p,q$としてその最近傍点をそれぞれ$p',q'$とする。
次の2つの量を考える。

a(p)=\frac{(pの最近傍点までの距離)}{(p'の最近傍点までの距離)}

a(q)=\frac{(qの最近傍点までの距離)}{(q'の最近傍点までの距離)}

$a(q)$はほぼ1となり、$a(p)$は非常に大きい値になる。
$q$の最近傍点$q'$は密集したクラスターの中にあるので、最近傍点までの距離が非常に小さいためである。
これは、($k=1$の場合の)局所外れ値度(LOF)の定義である。
この定義を$k>1$の場合に拡張する。
観測点$\boldsymbol{x'}$の$k$近傍を$N_k(\boldsymbol{x'})$と表す。
$N_k(\boldsymbol{x'})$の要素をすべて含み$\boldsymbol{x'}$を中心とする最小の球の半径を$\epsilon_k(\boldsymbol{x'})$と表す。
このとき、近傍有効距離という量を次のように定義する。

定義(近傍有効距離)　距離$d$が定義された$M$次元空間において、$\boldsymbol{u}$から$\boldsymbol{u'}$への近傍有効距離$l_k(\boldsymbol{u}→\boldsymbol{u'})$は次のように定義される。

l_k(\boldsymbol{u}→\boldsymbol{u'})=
\left\{\begin{array}{ll}
\epsilon_k(\boldsymbol{u'})&(\boldsymbol{u}\in N_k(\boldsymbol{u'})かつ\boldsymbol{u'}\in N_k(\boldsymbol{u}))\\
d(\boldsymbol{u},\boldsymbol{u'})&(それ以外)
\end{array}\right.

この近傍有効距離を使うと、局所外れ値の考え方に基づく異常度$a_{LOF}(\boldsymbol{x'})$は次のように定義される。

a_{LOF}(\boldsymbol{x'})=\frac{1}{k}\sum_{\boldsymbol{x}\in N_k(\boldsymbol{x'})}\frac{d_k(\boldsymbol{x'})}{d_k(\boldsymbol{x})}

ここで

d_k(\boldsymbol{u})=\frac{1}{k}\sum_{\boldsymbol{u'}\in N_k(\boldsymbol{u})}l_k(\boldsymbol{u}→\boldsymbol{u'})

ここではLocalOutlierFactorを使用して判定を行う。

from sklearn.neighbors import LocalOutlierFactor

# データをまとめる
X = np.concatenate([
np.array(list(x1)+list(x2)+[0.5,5]).reshape(-1,1),
np.array(list(y1)+list(y2)+[2,5.3]).reshape(-1,1)
], axis=1)

# ラベルを作成
ground_truth = np.ones(len(X), dtype=int) # 正常：1
ground_truth[-2] = -1 # 異常：-1

# 外れ値検出のモデルの作成
clf = LocalOutlierFactor(n_neighbors=10, contamination=0.05)
y_pred = clf.fit_predict(X)

# 判定とスコア
n_errors = (y_pred != ground_truth).sum()
X_scores = clf.negative_outlier_factor_

# 基のデータをプロット
plt.plot(x1,y1,'o')
plt.plot(x2,y2,'o')

plt.plot(0.5, 2, marker='*', color='red', markersize=10)
plt.text(0.8, 2, 'p', color='red')

plt.plot(5, 5, marker='*', color='green', markersize=10)
plt.text(5.3, 5, 'q', color='green')

#外れ値スコアに比例する半径で円をプロットする
radius = (X_scores.max() - X_scores) / (X_scores.max() - X_scores.min())

# 正常:青
plt.scatter(X[y_pred==1, 0], X[y_pred==1, 1], s=1000 * radius[y_pred==1], edgecolors='b',
            facecolors='none', label='Outlier scores')
# 異常:赤
plt.scatter(X[y_pred==-1, 0], X[y_pred==-1, 1], s=1000 * radius[y_pred==-1], edgecolors='r',
            facecolors='none', label='Outlier scores')
plt.xlabel("prediction errors: %d" % (n_errors))
plt.show()

赤い丸で囲われたデータ点が異常判定のもので、3つの点が異常と判定された。
これは近傍点の密度なども考慮された判定である。

カーネル密度推定

$M$次元データ$N$個からなる$D={\boldsymbol{x}^{(1)},\cdots,\boldsymbol{x}^{(N)}}$が与えられているとする。
カーネル密度推定法では、ある観測値$\boldsymbol{x}$と、$D$に含まれる観測値$\boldsymbol{x}^{(n)}$との間の類似度$K$を導入して、$\boldsymbol{x}$における確率密度を、

p(\boldsymbol{x}|H,D)=\frac{1}{N}\sum_{n=1}^NK_H(\boldsymbol{x},\boldsymbol{x}^{(n)})

のようにモデル化する。
ここでは$K$が、類似度の到達距離を表すパラメータ$H$を持つとしている。
$K_H$は一般に核関数またはカーネル関数と呼ぶ。
核関数としてもっともよく使われるのは正規分布である。

K_H(\boldsymbol{x},\boldsymbol{x}^{(n)})=N(\boldsymbol{x}|\boldsymbol{x}^{(n)},H)

特に、各変数を分散が1になるように個別に尺度変換した上で,$H=h^2|_M$のように単一の定数$h$のみをパラメータとして持つとしたモデル

K_h(\boldsymbol{x},\boldsymbol{x}^{(n)})=\biggl(\frac{1}{2\pi h^2} \biggr)^{M/2}\exp\biggl(-\frac{1}{2h^2}|\boldsymbol{x}-\boldsymbol{x}^{(n)}|^2 \biggr)

この核関数は、動径基底関数展開あるいはRBF展開とも呼ばれる。$h$または$H$のことをバンド幅と呼ぶ。

パラメータ$H$をデータから最適に求める方法は、積分二乗誤差

E(H|D)=\int d\boldsymbol{x}\{p_H(\boldsymbol{x})-p_真(\boldsymbol{x}) \}^2

を最小化するように決めることである。
通常、積分二乗誤差は

\begin{align}
E(H|D)&=\int d\boldsymbol{x}p_H(\boldsymbol{x})^2-2\int d\boldsymbol{x}p_真(\boldsymbol{x})p_H(\boldsymbol{x})+\int d\boldsymbol{x} p_真(\boldsymbol{x})^2\\
&\approx \int d\boldsymbol{x}p_H(\boldsymbol{x})^2-\frac{2}{N}\sum_{n=1}^Np_H^{(-n)}(\boldsymbol{x}^{(n)})+(定数)
\end{align}

第2項は、$p_真$を経験分布

p_{emp}(\boldsymbol{x})=\frac{1}{N}\sum_{n=1}^N\delta(\boldsymbol{x}-\boldsymbol{x}^{(n)})

で置き換えることで得られたものである。
さらに、$\boldsymbol{x}^{(n)}$をモデルから抜いたカーネル密度推定の表式

p_H^{-n}(\boldsymbol{x})=\frac{1}{N-1}\sum_{l=1;l\neq n}^N K_H(\boldsymbol{x},\boldsymbol{x}^{(l)})

を使う。

手順(カーネル密度推定におけるバンド幅推定)
1. $H$の候補値をあらかじめ$H^1,H^2,\cdots$と用意する
2. $H$の候補それぞれについて積分二乗誤差の値を計算し、記録する
3. 最小の積分二乗誤差を与える$H^i$を最適解として採用する

実行例

観測値$\boldsymbol{x}'$の異常度を

a(\boldsymbol{x}')=-\ln p(\boldsymbol{x}'|H,D)

により計算する。
データ$D$の中で異常度を計算する場合は、

a(\boldsymbol{x}^{(n)})=-\ln \biggl\{\frac{1}{N-1}\sum_{m\neq n}K_H(\boldsymbol{x}^{(n)},\boldsymbol{x}^{(m)}) \biggr\}

のように、自分自身をモデルから抜いた推定式で異常度を評価する。

KernelDensityでカーネル密度の推定を行う。

from sklearn.neighbors import KernelDensity

def kde2D(x, y, bandwidth, xbins=100, ybins=100):
    # カーネル密度推定
    xy_train = np.vstack([y, x]).T
    kde_skl = KernelDensity(bandwidth=bandwidth, kernel='gaussian')
    kde_skl.fit(xy_train)

    # 表示用に全体の密度を計算
    xx, yy = np.meshgrid(np.linspace(x.min(),x.max(),100),
                         np.linspace(y.min(),y.max(),100))
    xy_sample = np.vstack([yy.ravel(), xx.ravel()]).T

    z = np.exp(kde_skl.score_samples(xy_sample))

    # データ点に対する密度行列の計算
    xx_train, yy_train = np.meshgrid(x, y)
    xy_train_sample = np.vstack([yy_train.ravel(), xx_train.ravel()]).T

    K = np.exp(kde_skl.score_samples(xy_train_sample))

    return xx, yy, np.reshape(z, xx.shape), np.reshape(K, xx_train.shape)

x, y = davis['weight'], davis['height']

xx, yy, zz, K = kde2D(x, y, bandwidth=4, xbins=1000, ybins=1000)

#plt.pcolormesh(xx, yy, zz, shading='auto');
plt.contourf(xx, yy, zz, alpha=.8, levels=np.linspace(zz.min(),zz.max(),12))
plt.scatter(x, y, color='red', alpha=.5)
plt.xlim(40,110);
plt.ylim(140,190);

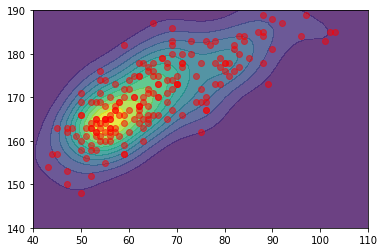
計算された密度関数を図に示す。
異常点が右下にあることがわかる。

データが集合している付近を拡大したものが下の図である。

異常度の計算を行う。

aa = np.sum(K, axis=0) - np.diag(K)
lowerLim = 10e-20
aa[aa<lowerLim] = lowerLim
a = (-1)*np.log(aa/(len(x)-1))

plt.plot(a, 'o');

1つだけ大きな異常度を持つ点がるが、これは右下のデータに対応するものである。

4. 分布がひと山にならない場合：クラスタリングに基づく方法

混合正規分布モデル

クラスター数を$K$とし、$k$番目のクラスターが、平均$\boldsymbol{\mu}_k$、共分散行列$\Sigma_k$の正規分布$N(\boldsymbol{x}|\boldsymbol{\mu}_k,\Sigma_k)$で表せるとする。
これは、条件付き確率の記号を使うと$p(\boldsymbol{x}|z=k)$となる。
ここで、$z$はクラスターの帰属先を示す確率変数で、値としては1から$K$までをとる。
$z$に応じて決まる確率値そのものをパラメータとして$p(z)=\pi_z$と表す。
当然、$\pi_1+\cdots+\pi_K=1$である。
想定する確率モデルは次の通りとなる。

p(\boldsymbol{x}|z)=N(\boldsymbol{x}|\boldsymbol{\mu}_z,\Sigma_z)\ および\ p(z)=\pi_z

$z$を周辺化により消去して、$\boldsymbol{x}$のみの分布を作ると次のようになる。

p(\boldsymbol{x}|\Theta)=\sum_{k=1}^K\pi_kN(\boldsymbol{x}|\boldsymbol{\mu}_k,\Sigma_k)

ただし、$K$個のクラスターのもつパラメータをまとめて$\Theta$

\Theta=\{\pi_1,\cdots,\pi_K,\boldsymbol{\mu}_1,\cdots,\boldsymbol{\mu}_K,\Sigma_1,\cdots,\Sigma_K\}

と表している。
クラスタリングの問題とは、$\Theta$をデータから求めた後に、$p(z|\boldsymbol{x},\Theta)$を求め、その最大値を求める問題である。
この$z$についての確率分布は、ベイズの定理から

p(z|\boldsymbol{x},\Theta)=\frac{p(\boldsymbol{x}|z)p(z)}{\sum_{z'=1}^Kp(\boldsymbol{x}|z')p(z')}=\frac{N(\boldsymbol{x}|\boldsymbol{\mu}_z,\Sigma_z)\pi_z}{\sum_{z'=1}^KN(\boldsymbol{x}|\boldsymbol{\mu}_z',\Sigma_z')\pi_z'}

手順(混合正規分布の期待値-最大化法)
1. 初期化:　混合正規分布のパラメータ

\hat{\Theta}=\{\hat{\pi}_1,\cdots,\hat{\pi}_K,\boldsymbol{\hat{\mu}}_1,\cdots,\boldsymbol{\hat{\mu}}_K,\hat{\Sigma}_1,\cdots,\hat{\Sigma}_K\}

に適当な初期値を設定する
2. 反復:　収束するまで以下を繰り返す
　a. 期待値ステップ:　現在のパラメータ推定値$\hat{\Theta}$を用いて、各標本の各要素への帰属度$q_k^{(n)}$を次式で求める

q_k^{(n)}=\frac{\hat{\pi}_kN(\boldsymbol{x}^{(n)}|\boldsymbol{\hat{\mu}}_k,\hat{\Sigma}_k)}{\sum_{l=1}^K\hat{\pi}_kN(\boldsymbol{x}^{(n)}|\boldsymbol{\hat{\mu}}_l,\hat{\Sigma}_l)}

　b. 最大化ステップ:　現在の帰属度$q_k^{(n)}$を基にして、パラメータ${\pi_k,\boldsymbol{\mu}_k}(k=1,\cdots,K)$の推定値を次式で求める

\hat{\pi}_k=\frac{1}{N}\sum_{n=1}^Nq_k^{(n)}\\
\hat{\boldsymbol{\mu}}_k=\frac{\sum_{n=1}^Nq_k^{(n)}\boldsymbol{x}^{(n)}}{\sum_{n=1}^Nq_k^{(n)}}

さらに、パラメータ${\Sigma}(k=1,\dots,K)$の推定値を次式で求める。

\hat{\Sigma}_k=\frac{\sum_{n=1}^Nq_k^{(n)}(\boldsymbol{x}^{(n)}-\boldsymbol{\hat{\mu}}_k)(\boldsymbol{x}^{(n)}-\boldsymbol{\hat{\mu}}_k)^T}{\sum_{n=1}^Nq_k^{(n)}}

これらを新しいパラメータ推定値$\hat{\Theta}$とする

実行例

異常度は次のように定義する。

a(\boldsymbol{x'})=-\ln\biggl\{\sum_{k=1}^K\hat{\pi}_kN(\boldsymbol{x}'|\boldsymbol{\hat{\mu}}_k,\hat{\Sigma}_k) \biggr\}

混合正規分布を異常検知に使う際は、異常標本がいつも含まれないように慎重にデータのクレンジングを行う必要がある。
BayesianGaussianMixtureを使って混合ガウス分布の計算を行う。

from sklearn.mixture import BayesianGaussianMixture
from scipy.stats import multivariate_normal

# データの準備
x = davis[['weight', 'height']]
xx = x[x.index!=12]

# 混合ガウスモデルによるクラスタリング
# 異常点を除いて学習させる
vbgm = BayesianGaussianMixture(n_components=10, random_state=6)
vbgm.fit(xx)

# 各分布の重み
use_idx = vbgm.weights_>0.1 # 0.1以下のものは使用しない

計算された分布を確認する。

# ラベル
labels=vbgm.predict(x)

# 色の設定
cmaps = ['Purples', 'Blues', 'Reds', 'Greens']

# 表示用のグリッド
xm, ym = np.meshgrid(np.linspace(xx['weight'].min(),xx['weight'].max(),100),
                     np.linspace(xx['height'].min(),xx['height'].max(),100))  
xy_sample = np.vstack([xm.ravel(), ym.ravel()]).T

# 各ガウス分布における等高線の表示
for i, (m, c) in enumerate(zip(vbgm.means_, vbgm.covariances_)):
    if use_idx[i]:
        mp = multivariate_normal(m, c).pdf(xy_sample).reshape(100,100)
        plt.contour(xm, ym, mp, levels=3, cmap=cmaps[i])

plt.scatter(x['weight'],x['height'], c=labels)
plt.scatter(x.loc[a>250, 'weight'],x.loc[a>250, 'height'], color='green')
plt.scatter(vbgm.means_[use_idx,0],vbgm.means_[use_idx,1], color='red')

クラスタは2つと計算されたので、図に示して確認を行う。

右下にある異常点があるので、データが集合している部分を拡大する。

異常値の計算を行う。

mp = np.array([multivariate_normal(m, c).pdf(x) for i, (m, c) in enumerate(zip(vbgm.means_, vbgm.covariances_)) if use_idx[i]])
pi = vbgm.weights_[use_idx]

a = -np.log(pi@mp)

plt.plot(a, 'o');

1つだけ大きな異常値を持つ点が存在するが、これは散布図の右下の点に対応するものである。

6. 支持ベクトルデータ記述法に基づく異常判定

データ$D={\boldsymbol{x}^{(1)},\cdots,\boldsymbol{x}^{(N)}}$が与えられたときに、データのほぼ全体を囲む球を考え、その球に入りきらなかったものを異常とする。
これは1クラスサポートベクトルマシンと呼ばれる手法である。

データを含むという条件の下で、できる限り小さい球を求める。
これは次のような最適化問題として表せる。

\min_{R,\boldsymbol{b}}R^2\ subject\ to\ |\boldsymbol{x}^{(n)}-\boldsymbol{b}|^2\leq R^2

ここで$\boldsymbol{x}^{(n)}$に対して、半径の2乗に$u^{n}$分だけ許容した上で問題を解く。

\min_{R,\boldsymbol{b},\boldsymbol{u}}\biggl\{R^2+C\sum_{n=1}^Nu^{(n)} \biggr\}\ subject\ to\ |\boldsymbol{x}^{(n)}-\boldsymbol{b}|^2\leq R^2+u^{(n)}

この問題の解を$(R^,\boldsymbol{b}^,\boldsymbol{u}^*)$とする。
異常度は直感的に「球からはみ出した長さ」として

a(\boldsymbol{x}')=|\boldsymbol{x}'-\boldsymbol{b}^*|^2-R^{*2}

のように定義できる。2乗を展開して、

a(\boldsymbol{x}')=\kappa(\boldsymbol{x}',\boldsymbol{x}')-2\kappa(\boldsymbol{b}^*,\boldsymbol{x}')+\kappa(\boldsymbol{b}^*,\boldsymbol{b}^*)-R^{*2}

と表しておく。ただし、$\kappa(・)$は引数同士の内積を表す。
カーネルトリックとは、内積の定義を、もともとの$\kappa(\boldsymbol{x}',\boldsymbol{x}^{(n)})=\boldsymbol{x}'^T\boldsymbol{x}^{(n)}$から、適切な条件を満たす関数、例えば、

\kappa(\boldsymbol{x}',\boldsymbol{x}^{(n)})=\exp\bigl(-\sigma|\boldsymbol{x}'-\boldsymbol{x}^{(n)}|^2 \bigr)

に置換することを意味する。これはRBFカーネルと呼ぶ。
カーネルトリックを利用すれば、非線形な関係を、非線形変換を明示的に与えなくても扱える。

OneClassSVMを使って異常判定を行う。
学習用のデータにおける異常点数の割合を指定する。

from sklearn.svm import OneClassSVM
from sklearn.preprocessing import StandardScaler

# 標準化
scaler = StandardScaler()
data_scaled = scaler.fit_transform(davis[['weight', 'height']])

# OCSVMモデル作成
ocsvm = OneClassSVM(nu=0.05, kernel='rbf', gamma='auto')
ocsvm.fit(data_scaled)

# 表示用のグリッドを用意
x, y = data_scaled[:,0], data_scaled[:, 1]
xx, yy = np.meshgrid(np.linspace(x.min(),x.max(),100),
                     np.linspace(y.min(),y.max(),100))
xy_sample = np.vstack([xx.ravel(), yy.ravel()]).T

# decision_functionで超平面からの距離
y_pred = ocsvm.decision_function(xy_sample).reshape(100,100)

# predictで判定結果(正常:1,異常:-1)
Z = ocsvm.predict(xy_sample).reshape(100,100)

# 標準化したデータを元に戻す
data_inv = scaler.inverse_transform(np.vstack([np.linspace(x.min(),x.max(),100), np.linspace(y.min(),y.max(),100)]).T)

# 支持ベクトルも元の単位に変換
supports = scaler.inverse_transform(ocsvm.support_vectors_)

# データの表示
plt.contourf(data_inv[:,0], data_inv[:,1], y_pred, levels=15, alpha=.5)
plt.contour(data_inv[:,0], data_inv[:,1], Z, levels=[0], alpha=.5)
plt.scatter(davis['weight'],davis['height'], color='red')
plt.scatter(supports[:,0], supports[:,1], color='blue')
plt.xlim(40,110);
plt.ylim(140,);

黒い線が異常判定の境界線、青い点が支持ベクトルである。

次回

不要な次元を含むデータからの異常検知

参考文献