pythonで「計量時系列分析」を読む1 時系列分析の基礎概念

時系列分析で有名な「計量時系列分析」をpythonで実装しながら読み進めていきます。
汚いコードですが自主学習・記録が目的ですのでご了承ください。
様々な人がより分かりやすい記事を書いていますのでそちらをご覧ください。
そして、本格的に勉強したい方・細かい内容を知りたい方はぜひ参考書を手に取って勉強してください。
また、何か問題があればご連絡いただければと思います。

次の本を扱います。

参考書

基本統計量と時系列モデル

自己共分散は、同一の時系列データにおける異時点間の共分散である。たとえば1次の自己共分散は、
$$
\gamma_{1t}=Cov(y_t,y_{t-1})=E[(y_t-\mu_t)(y_{t-1}-\mu_{t-1})]
$$
で定義される。ここで、$\mu_{t-1}=E(y_{t-1})$である。
一般的に$k$次の自己共分散は
$$
\gamma_{kt}=Cov(y_t,y_{t-k})=E[(y_t-\mu_t)(y_{t-k}-\mu_{t-k})]
$$
で定義される。ここで、$\mu_{t-k}=E(y_{t-k})$である。
自己共分散を$k$の関数として見たものは自己共分散関数と呼ばれる。
自己共分散は値が単位に依存してしまう問題がある。
自己共分散を基準化したものが自己相関係数であり、$k$次の自己相関係数は
$$
\rho_{kt}=Corr(y_t,y_{t-k})=\frac{Cov(y_t,y_{t-k})}{\sqrt{Var(y_t)Var(y_{t-k})}}=\frac{\gamma_{kt}}{\sqrt{\gamma_{0t}\gamma_{0,t-k}}}
$$
で定義される。$\rho_{0t}=1$であることは明らかであり、$k\geq1$において$|\rho_{kt}|\leq 1$も成立する。
自己相関係数を$k$の関数として見たものは自己相関関数と呼ばれ、自己相関関数をグラフに描いたものはコレログラムと呼ばれる。

import numpy as np
import matplotlib.pyplot as plt

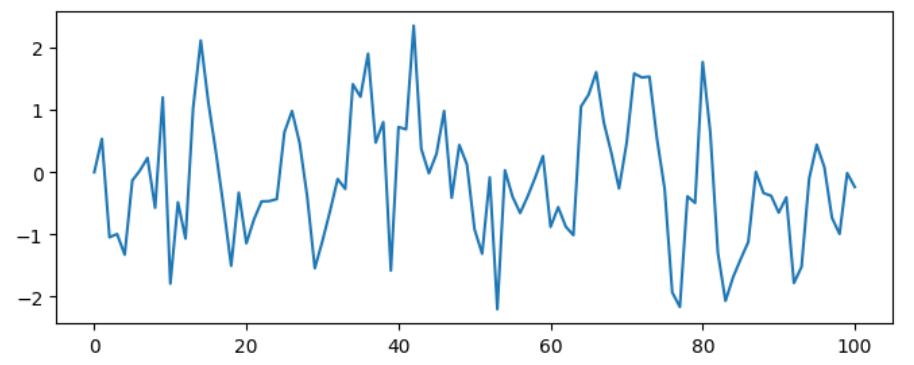
# 時系列データの生成
y = [0]
for _ in range(100):
    y.append(0.5*y[-1]+np.random.normal())

plt.figure(figsize=(8,3))
plt.plot(y)

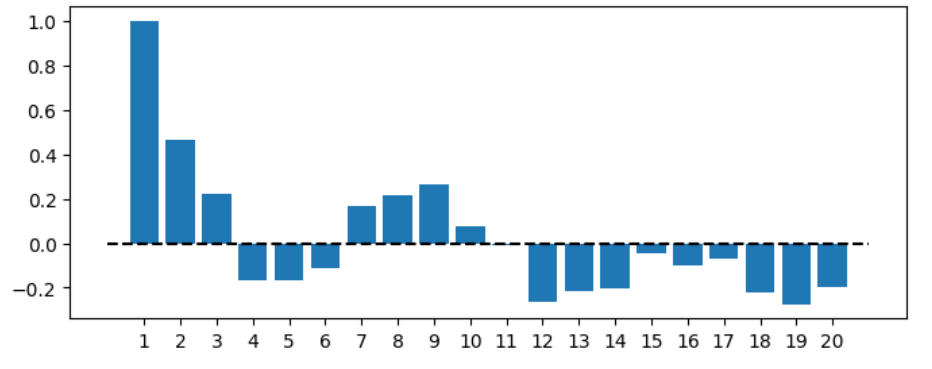
# 自己相関係数の計算
cor = [1]
for i in range(1,20):
    cor.append(np.corrcoef(y[:-i],y[i:])[0,1])

# 図示
plt.figure(figsize=(8,3))
plt.bar(np.arange(1,21), cor)
plt.hlines(0, 0, 21, linestyle='--', color='black')
plt.xticks(np.arange(1,21));

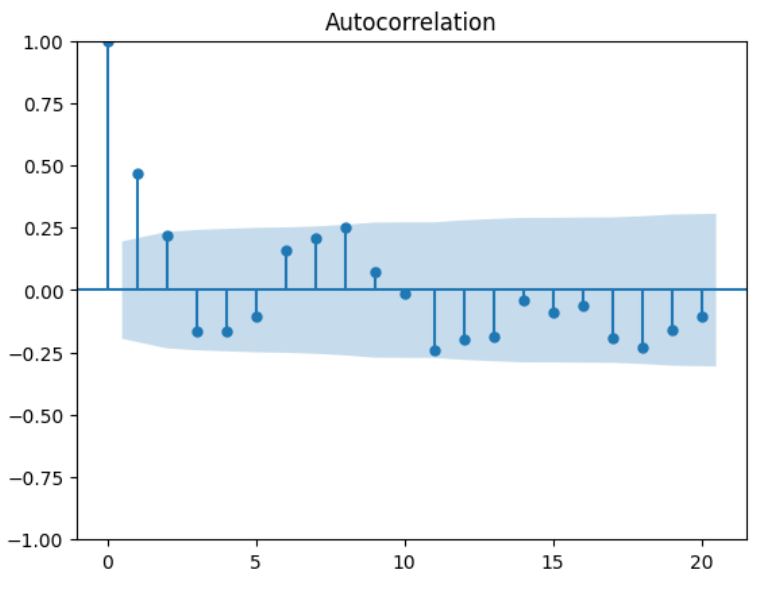
ライブラリstatsmodelsにも自己相関係数の計算及び可視化を行う関数が用意されている。

import statsmodels.api as sm

# 自己相関係数の計算
p_acf = sm.tsa.stattools.acf(y)
print(p_acf)

# 自己相関係数の可視化
sm.graphics.tsa.plot_acf(y, lags=20);

[ 1.          0.46564607  0.21845721 -0.16503196 -0.16470934 -0.10819501
  0.16045977  0.21029244  0.25334663  0.07294192 -0.01094577 -0.2431834
 -0.19864032 -0.18425037 -0.04240966 -0.09028844 -0.06073843 -0.19202027
 -0.23020201 -0.16109122 -0.10494409]

定常性

定常性とは、同時分布や基本統計量の時間不変性に関するものであり、何を不変とするかによって、弱定常性と強定常性の2つに分類される。

定義(弱定常性)
任意の$t$と$k$に対して
$$
\begin{align}
E(y_t)&=\mu\
Cov(y_t,y_{t-k})&=E[(y_t-\mu)(y_{t-k}-\mu)]=\gamma_k
\end{align}
$$
が成立する場合、過程は弱定常性といわれる。

定常過程においては、自己共分散は時点には依存せずに時間差$k$のみに依存することになる。
したがって、任意の$k$に対して、$\gamma_k=\gamma_{-k}$が成立する。
自己相関は
$$
Corr(y_t,y_{t-k})=\frac{\gamma_{kt}}{\sqrt{\gamma_{0t}\gamma_{0,t-k}}}=\frac{\gamma_k}{\gamma_0}=\rho_k
$$
となり、自己相関も時点に依存しなくなる。さらに、$\rho_k=\rho_{-k}$が成立する。
弱定常性は共分散定常性と呼ばれることもある。

定義(強定常性)
任意の$t$と$k$に対して$(y_t,y_{t+1},\cdots,y_{t+k})'$の同時分布が同一となる場合、過程は強定常といわれる。ここで、$\boldsymbol{y}'$はベクトル$\boldsymbol{y}$の転置を表す。

ホワイトノイズ

最も基礎的な強定常過程の例としては、次のiid系列がある。

定義(iid系列)
各時点のデータが互いに独立でかつ同一の分布に従う系列はiid系列と呼ばれる。

$y_t$が期待値$\mu$、分散$\sigma^2$のiid系列であることを$y_t\sim iid(\mu,\sigma^2)$と表記する。
期待値0のiid系列は時系列モデルの撹乱項として用いることができる。

定義(ホワイトノイズ)
すべての時点において

E(\varepsilon_t)=0\\
\gamma_k=E(\varepsilon_t\varepsilon_{t-k})=
\left\{\begin{array}{ll}
\sigma^2 & k=0\\
0 & k\neq 0
\end{array}\right.

が成立するとき、$\varepsilon_t$はホワイトノイズと呼ばれる。

$\varepsilon_t$が分散$\sigma^2$のホワイトノイズであることを$\varepsilon_t\sim W.N.(\sigma^2)$と表記する。
正規過程に従うホワイトノイズは正規ホワイトノイズと呼ばれ、$\varepsilon_t$が分散$\sigma^2$の正規ホワイトノイズに従うことを$\varepsilon_t\sim iid N(0,\sigma^2)$と表記する。
最も基礎的な(弱)定常過程は、ホワイトノイズを用いて
$$
y_t=\mu+\varepsilon_t,\ \varepsilon_t\sim W.N.(\sigma^2)
$$
とするものである。このモデルは、
$$
y_t=\mu+\sqrt{\sigma^2}\varepsilon_t,\ \varepsilon_t\sim W.N.(1)
$$
という表現をすることもできる。

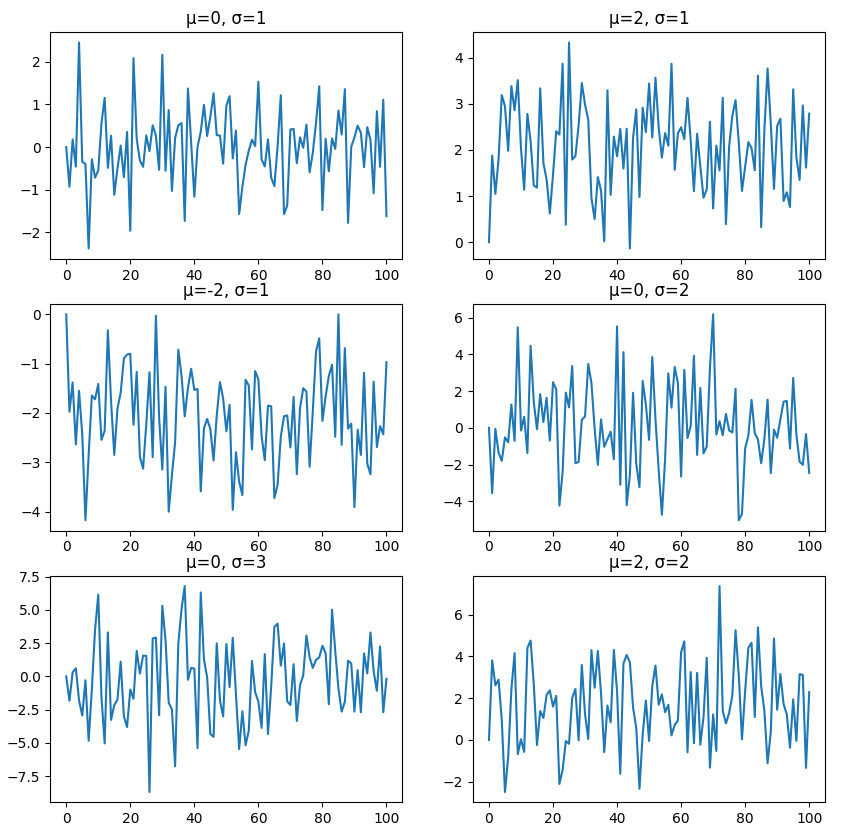
# 様々な条件
mus = [0, 2, -2, 0, 0, 2]
sigmas = [1, 1, 1, 2, 3, 2]

# 各条件における時系列データの生成・可視化
fig, ax = plt.subplots(3, 2, figsize=(10,10))
for i, (mu, sigma) in enumerate(zip(mus, sigmas)):
    y = [0]
    [y.append(mu+np.random.normal(scale=sigma)) for _ in range(100)]
    ax[i//2][i%2].plot(y)
    ax[i//2][i%2].set_title('μ='+str(mu)+', σ='+str(sigma))

自己相関の検定

自己相関の検定を行うためには、まず自己相関の推定値を計算する必要がある。
定常性の仮定の下では期待値や自己相関などの基本統計量は時点に依存しないので、データから対応する標本統計量を計算することで自然な推定量を得ることができる。
すなわち、期待値、自己共分散、自己相関の推定量は

\begin{align}
\bar{y}&=\frac{1}{T}\sum_{t=1}^Ty_t\\
\hat{\gamma}_k&=\sum_{t=k+1}^T(y_t-\bar{y})(y_{t-k}-\bar{y}),\ k=0,1,2,\cdots\\
\hat{\rho}_k&=\frac{\hat{\gamma}_k}{\hat{\gamma}_0},\ k=1,2,3,\cdots
\end{align}

で与えられ、それぞれ標本平均、標本自己共分散、標本自己相関係数と呼ばれる。

標本自己相関係数$\hat{\rho}_k$を用いて、$H_0:\rho_k=0$という帰無仮説を$H_1:\rho_k\neq0$という対立仮説に対して検定するためには、帰無仮説の下での$\hat{\rho}_k$の漸近分布を求める必要がある。
$y_t$がiid系列の場合には$\hat{\rho}_k$が漸近的に平均0、分散$1/T$の正規分布に従うことが知られている。
$|\hat{\rho}_k|$が$1.96/\sqrt{T}$より大きければ、$H_0:\rho_k=0$という帰無仮説は有意水準5%で棄却され、有意な$k$次自己相関を持つことになる。

# 系列長
T = 100

# 時系列データの生成
y = [0]
for _ in range(T):
    y.append(0.5*y[-1]+np.random.normal())

# 自己相関係数の計算
y_bar = np.mean(y)
gamma_bar = [np.sum((y-y_bar)**2)]
for i in range(1,T):
    gamma_bar.append(np.sum((y[:-i]-y_bar)*(y[i:]-y_bar)))
rho_bar = gamma_bar / gamma_bar[0]

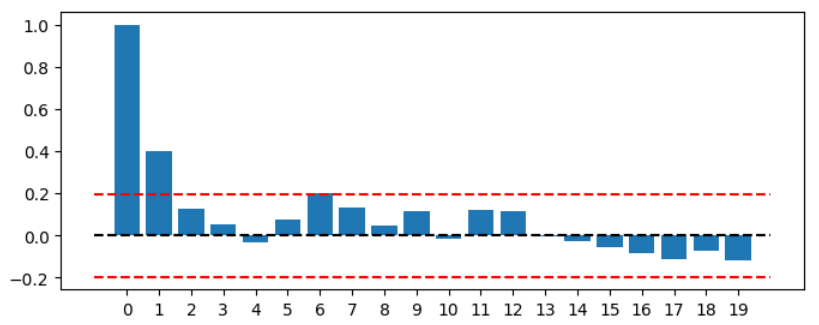
# 可視化・検定
plt.figure(figsize=(8,3))
plt.bar(np.arange(0,20), rho_bar[:20])
plt.hlines(0, -1, 20, linestyle='--', color='black')
plt.hlines([-1.96/np.sqrt(T),1.96/np.sqrt(T)], -1, 20, linestyle='--', color='red')
plt.xticks(np.arange(0,20));

# 自己相関係数の計算
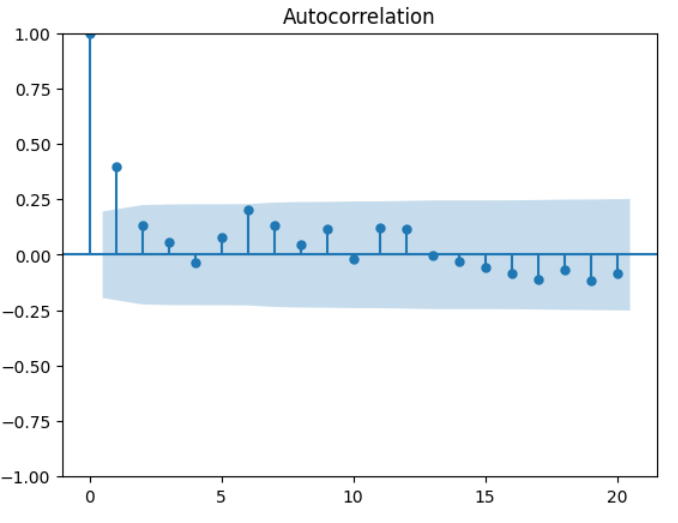
p_acf = sm.tsa.stattools.acf(y)
print(p_acf)

# 自己相関係数の可視化
sm.graphics.tsa.plot_acf(y, lags=20);

[ 1.          0.39950382  0.1300835   0.0557919  -0.03281945  0.07795338
  0.20015898  0.13303618  0.04781549  0.11700213 -0.01766644  0.12011396
  0.11593244 -0.00160565 -0.0291234  -0.05595282 -0.08543759 -0.11151328
 -0.07029338 -0.11563084 -0.08203962]

複数の自己相関係数がすべて0であるという帰無仮説を検定したいとき、つまり$H_0:\rho_1=\rho_2=\cdots=\rho_m=0$という帰無仮説を、$H_1:$少なくとも1つの$k\in [1,m]$において$\rho_k\neq 0$という対立仮説に対してする検定はかばん検定と呼ばれる。
よく使われる統計量としては、
$$
Q(m)=T(T+2)\sum_{k=1}^m\frac{\hat{\rho}_k^2}{T-k}\sim \chi^2(m)
$$
がある。ここで、$\chi^2(m)$は自由度$m$のカイ２乗分布を表す。

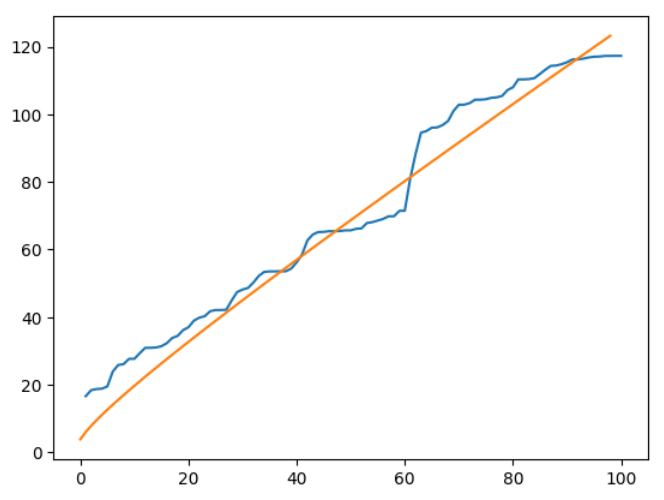
from scipy.stats import chi2

# かばん検定の統計量の計算
Q = T*(T+2)*np.cumsum(rho_bar[1:]**2/(T-np.arange(1,T)))

# カイ二乗分布の値
c2 = chi2.ppf(0.95, df=np.arange(1,100))

# 可視化・比較
plt.plot(Q)
plt.plot(c2)

95%点より大きな値を取ることが確認できる。

ライブラリstatsmodelsにかばん検定を行うacorr_ljungboxという関数が用意されている。

from statsmodels.stats.diagnostic import acorr_ljungbox

# かばん検定の統計量の計算
result = acorr_ljungbox(y, lags = 100)

# 結果の表示
display(result.head())

# 可視化
plt.plot(result['lb_stat'])
plt.plot(c2)

	lb_stat	lb_pvalue
1	16.603532	0.000046
2	18.381679	0.000102
3	18.712106	0.000314
4	18.827624	0.000850
5	19.486126	0.001560

同様の結果が得られていることが確認できた。
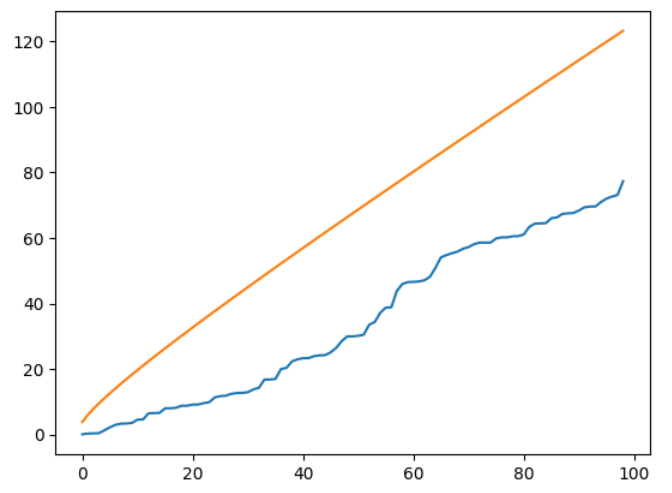
次に自己相関のない場合を確認する。

# 自己相関のない場合の時系列データの生成
y = [0]
for _ in range(T):
    y.append(np.random.normal())

# 自己相関係数の計算
y_bar = np.mean(y)
gamma_bar = [np.sum((y-y_bar)**2)]
for i in range(1,T):
    gamma_bar.append(np.sum((y[:-i]-y_bar)*(y[i:]-y_bar)))
rho_bar = gamma_bar / gamma_bar[0]

# かばん検定の統計量の計算
Q = T*(T+2)*np.cumsum(rho_bar[1:]**2/(T-np.arange(1,T)))

# カイ二乗分布の値
c2 = chi2.ppf(0.95, df=np.arange(1,100))

# 可視化・比較
plt.plot(Q)
plt.plot(c2)

# かばん検定の統計量の計算
result = acorr_ljungbox(y, lags = 100)

# 結果の表示
display(result.head())

# 可視化
plt.plot(result['lb_stat'])
plt.plot(c2)

	lb_stat	lb_pvalue
1	0.062688	0.802297
2	0.304728	0.858676
3	0.341048	0.952132
4	0.426034	0.980290
5	1.291123	0.935842

自己相関のない場合は95%点より小さな値を取ることが確認できた。

演習問題の一部に取り組む。
まずは、データ及び対数差分系列の計算を行い可視化する。

import pandas as pd

# 各種データの読み込み
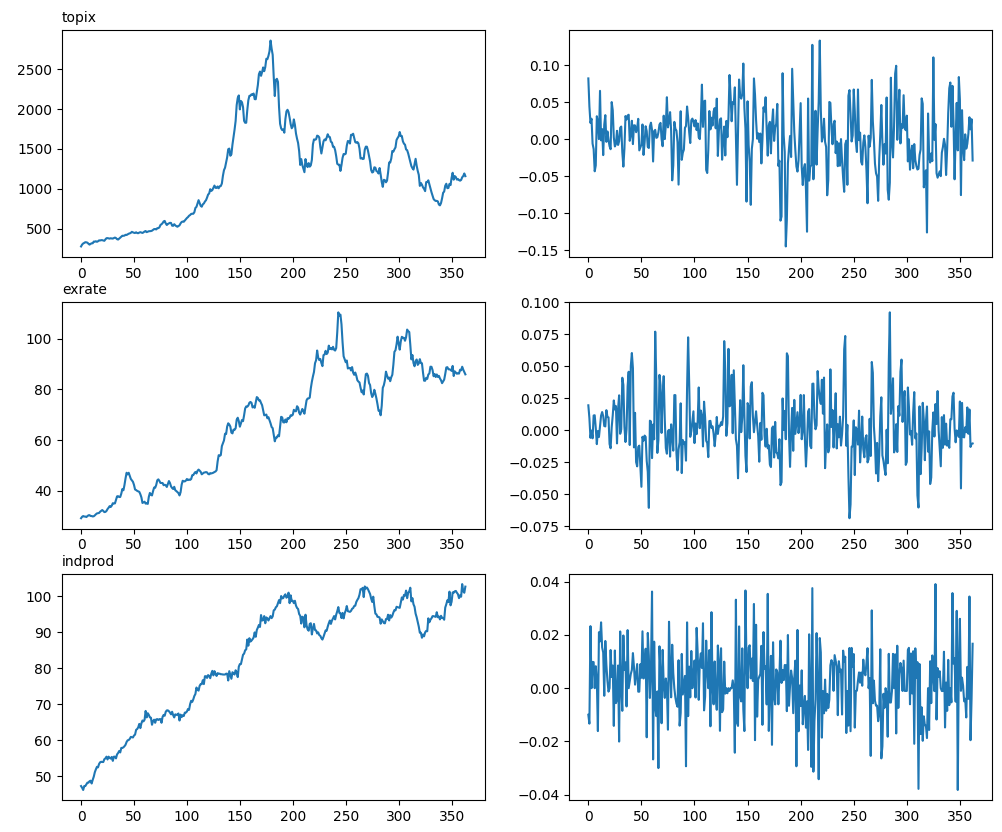
df = pd.read_excel('economicdata.xls')
y1 = df['topix'].values
y2 = df['exrate'].values
y3 = df['indprod'].values

# 対数差分系列の計算
y_rate1 = np.log(y1)[1:] - np.log(y1)[:-1]
y_rate2 = np.log(y2)[1:] - np.log(y2)[:-1]
y_rate3 = np.log(y3)[1:] - np.log(y3)[:-1]

# 各時系列データの可視化
fig, ax = plt.subplots(3,2,figsize=(12,10))
ax[0][0].plot(y1)
ax[0][1].plot(y_rate1)
ax[1][0].plot(y2)
ax[1][1].plot(y_rate2)
ax[2][0].plot(y3)
ax[2][1].plot(y_rate3)

ax[0][0].set_title('topix', loc='left',fontdict={'fontsize':10})
ax[1][0].set_title('exrate', loc='left',fontdict={'fontsize':10})
ax[2][0].set_title('indprod', loc='left',fontdict={'fontsize':10})

次に自己相関係数の計算及びかばん検定の統計慮の計算を行う。

# 系列長
T = len(y_rate1)

# カイ二乗分布の値
c2 = chi2.ppf(0.95, df=np.arange(1,T))

# 各データにおける自己相関係数の計算及びかばん検定
fig, ax = plt.subplots(3,2,figsize=(12,10))
for k, y in enumerate([y_rate1,y_rate2,y_rate3]):
    # 自己相関係数の計算
    y_bar = np.mean(y)
    gamma_bar = [np.sum((y-y_bar)**2)]
    for i in range(1,T):
        gamma_bar.append(np.sum((y[:-i]-y_bar)*(y[i:]-y_bar)))
        rho_bar = gamma_bar / gamma_bar[0]
    
    # かばん検定の統計量の計算
    Q = T*(T+2)*np.cumsum(rho_bar[1:]**2/(T-np.arange(1,T))) 
    
    # 可視化(自己相関係数)
    ax[k][0].bar(np.arange(1,20), rho_bar[1:20])
    ax[k][0].hlines(0, 0, 20, linestyle='--', color='black')
    ax[k][0].hlines([-1.96/np.sqrt(T),1.96/np.sqrt(T)], 0, 20, linestyle='--', color='red')
    
    # 可視化(かばん検定)
    ax[k][1].plot(Q)
    ax[k][1].plot(c2)

ax[0][0].set_title('topix', loc='left',fontdict={'fontsize':10})
ax[1][0].set_title('exrate', loc='left',fontdict={'fontsize':10})
ax[2][0].set_title('indprod', loc='left',fontdict={'fontsize':10})

かばん検定の統計量がいずれも95%点よりも大きいため、いずれも自己相関を持っているといえる。
これはライブラリstatsmodelsを使ってより簡単に求められる。

T = len(y_rate1)
c2 = chi2.ppf(0.95, df=np.arange(1,T))

fig, ax = plt.subplots(3,2,figsize=(12,10))
for k, y in enumerate([y_rate1,y_rate2,y_rate3]):
    # 自己相関係数の可視化
    sm.graphics.tsa.plot_acf(y, lags=np.arange(1,20), ax=ax[k][0], auto_ylims=True); 
    
    # かばん検定の統計量の計算
    Q = acorr_ljungbox(y, lags = T-1)
    
    # 可視化(かばん検定)
    ax[k][1].plot(Q['lb_stat'])
    ax[k][1].plot(c2)

ax[0][0].set_title('topix', loc='left',fontdict={'fontsize':10})
ax[1][0].set_title('exrate', loc='left',fontdict={'fontsize':10})
ax[2][0].set_title('indprod', loc='left',fontdict={'fontsize':10})

以上となります。

次回

ARMA過程