「異常検知と変化検知」は異常検知の本です。アルゴリズム部分をpythonで実装していきたいと思います。たくさんの方が同じ内容をより良い記事でとして投稿しています。
個人的な勉強のメモ書きとなります。
コードがかなり汚いです。申し訳ありません。
実装コードの安定性がありませんのでご了承ください。
まとめることが目的ではないので本文について参考書とほぼ同じ表現となっています。問題があればお教えください。
興味を持ったり、導出や詳細などを知りたい方は「異常検知と変化検知」を読んでいただければと思います。
参考
前回
近傍法による異常検知
混合分布モデルによる逐次更新型異常検知
混合分布モデルとその逐次更新
実データの解析においては、系がいくつかの異なる動作モードを持つ場合がある。
混合モデルとはこれらを確率分布として表現したもので、次のような形をとる。
$$
p(\boldsymbol{x}|\Theta)=\sum_{i=1}^K\pi_kp_k(\boldsymbol{x}|\boldsymbol{\theta}_k),\ \pi_1+\cdots+\pi_K=1
$$
ただし、$p_k(\boldsymbol{x}|\boldsymbol{\theta}_k)$は$\boldsymbol{x}$について規格化された確率分布である。
$\boldsymbol{\theta}_k$は第$k$番目の分布に含まれるパラメータ、$\Theta$は右辺に現れる未知パラメータの集まりを表す記号で、明示的に書くと
$$
\Theta={\pi_1,\cdots,\pi_K,\boldsymbol{\theta}_1,\cdots,\boldsymbol{\theta}_K }
$$
である。
和の中の第$k$項を第$k$要素(またはコンポーネント、クラスター)と呼ぶ。
また、$\pi_k$を第$k$クラスターの混合重みと呼ぶ。
データ$D$が${\boldsymbol{x}^{(1)},\boldsymbol{x}^{(2)},\cdots,\boldsymbol{x}^{(N)} }$のように与えられれば、混合分布のパラメータ$\Theta$は最尤推定で原理的には求められる。
$$
L(\Theta|D)=\sum_{n=1}^N\ln{\sum_{k=1}^K}\pi_kp_k(\boldsymbol{x}^{(n)}|\boldsymbol{\theta}_k)
$$
対数の中に総和が入っているために、各パラメータによる微分を0と置いても簡単な式にはならず、解析的に最適解を求めることはできない。
一般に混合分布のパラメータ推定のためには、EM法と呼ばれる手法が使われる。
混合分布モデルにおいて確率分布$p_l(\boldsymbol{x}|\boldsymbol{\theta}_k)$として正規分布$N(\boldsymbol{x}|\boldsymbol{\mu}_k,\Sigma_k)$を選んだものを混合正規分布と呼ぶ。
この場合$\boldsymbol{\theta}_k={\boldsymbol{\mu}_k ,\Sigma_k}$となる。
実用上「直近の観測値は重視するが古い観測値は徐々に忘れたい」という状況がある。
これは観測された標本に異なる重みを考えることで実現できる。
混合正規分布の対数尤度の式において、
$$
L(\Theta|D)=\sum_{n=1}^tw_t^{(n)}\ln{\sum_{k=1}^K}\pi_kN(\boldsymbol{x}^{(n)}|\boldsymbol{\mu}_k,\Sigma_k)
$$
のように標本番号$n$ごとに異なる重み$w_t^{(n)}$を導入する。
ここで、時刻$t$までに観測された標本集合を$D^{(t)}={\boldsymbol{x}^{(1)},\cdots,\boldsymbol{x}^{(t)} }$と書いた。
モデルの推定は、時刻$t$の時点までに得られたデータに基づいて行うことになる。
一般に、観測値を得るたびに重みを振りなおすので、重みは現在の時刻$t$にも依存する。
時刻$t-1$において、モデルのパラメータ
$$
\Theta={\pi_1,\cdots,\pi_K,\boldsymbol{\mu}_1,\cdots,\boldsymbol{\mu}_K,\Sigma_1,\cdots,\Sigma_K }
$$
の数値が得られていると仮定する。
時刻$t$において観測した標本$\boldsymbol{x}^{(t)}$だけを使い(それ以前のデータを参照することなしに)、
$L(\Theta|D^{(t)})$を最大化するように、パラメータ$\Theta$を更新する
手元にある訓練標本全部を使ってモデルを学習する方法を一括型学習(バッチ学習) と呼ぶ。
これに対して、標本を観測するたびにモデルを修正していくタイプの学習方法を逐次更新型学習(オンライン学習) と呼ぶ。
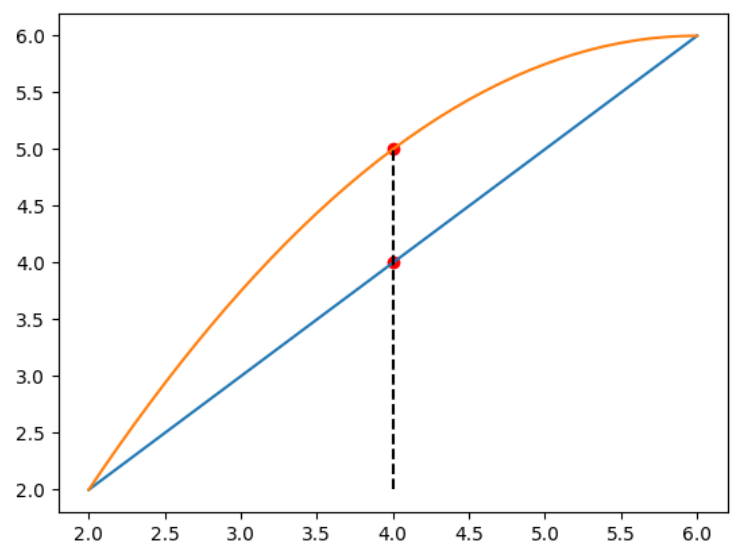
イエンセンの不等式による和と対数関数の順序交換
イエンセンの不等式は次のような関係式である。
$c_1+\cdots+c_K=1$を満たす非負の係数${c_i}$に対して、次式が成り立つ。
$$
\ln{\biggl(\sum_{k=1}^Kc_kX_k \biggr)}\geq \sum_{k=1}^Kc_k\ln{(X_k)}
$$
等号が成り立つのは$X_1=\cdots=X_K$のときに限られる。
連続変数の場合、任意の確率分布$q(\boldsymbol{x})$が可積分な関数$g(\boldsymbol{x})$に対して、次式が成り立つ。
$$
\ln{\int d\boldsymbol{x}q(\boldsymbol{x})g(\boldsymbol{x})}\geq\int d\boldsymbol{x}q(\boldsymbol{x})\ln{g(\boldsymbol{x})}
$$
EM法では、イエンセンの不等式で対数尤度の下限を求め、その下限を最大化することで本体を最大化する。
対数尤度にイエンセンの不等式を適用すると次のような下限の式が得られる。
$$
L_{下限}(\Theta|D^{(t)})=\sum_{n=1}^tw_t^{(n)}\sum_{k=1}^Kq_k^{(n)}\ln{\frac{\pi_kN(\boldsymbol{x}^{(n)}|\boldsymbol{\mu}_k),\Sigma_k}{q_k^{(n)}}}
$$
import numpy as np
import matplotlib.pyplot as plt
# イエンセンの不等式の説明の図
x = np.arange(2,6.1, 0.1)
y1 = x
y2 = -1/4*(x-6)**2+6
plt.plot(x, y1);
plt.plot(x, y2);
plt.vlines(4, 2, 5, linestyles='--', color='black');
plt.scatter(4, 4, color='red');
plt.scatter(4, 5, color='red');
EM法による重み付き対数尤度の最大化
導出された重み付き対数尤度の下限を使って、パラメータの最尤推定を行う。
下限には、もともとのパラメータ${\pi_k,\boldsymbol{\mu}_k,\Sigma_k}$と、イエンセンの不等式を使う際に導入した${q_k^{(t)}}$という2種類の未知量がある。
EM法では、片方を既知として片方を求める、という具合に両者を求めていく。
帰属度qk(n)についての最適化
推定値 ${\pi_k,\mu_k,\Sigma_k}$ が数値として手元に与えられているとする。
この前提だと$L_{下限}(\Theta|D^{(t)})$に含まれる未知量は${q_k^{(t)}}$だけであるので、これを最適に決める。
ラグランジュ法から解として、
q_k^{(n)}=\frac{\pi_kN(\boldsymbol{x}^{(n)}|\boldsymbol{\mu}_k,\Sigma_k)}{\sum_{l=1}^K\pi_lN(\boldsymbol{x}^{(n)}|\boldsymbol{\mu}_l,\Sigma_l)}
が得られる。
$q_k^{(n)}$は、標本$\boldsymbol{x}^{(n)}$が与えられときに、その標本が第$k$クラスターに所属する確率を表す。
これを特に、標本$\boldsymbol{x}^{(n)}$の第$k$クラスターへの**帰属度(もしくは負担率)**と呼ぶ。
混合重みの最適化
帰属度$q_k^{(n)}$が数値として求められている前提で、まず${\pi_k}$について考える。
ラグランジュ乗数を使って微分をすることで、
\hat{\pi}_k^{(t)}=\frac{1}{\sum_{n'=1}^tw_t^{(n')}}\sum_{n=1}^tw_t^{(n)}q_k^{(n)}
という解が求められる。
平均と共分散の最適化
残るパラメータ${\boldsymbol{\mu}_k,\Sigma_k}$についても混合重みと同様に、
${q_k^{(n)}}$が数値として求まっているという前提で、重み付き対数尤度の下限を最大化することでパラメータを求める。
今回は制約条件はないので簡単に計算できる。
解として、
\hat{\boldsymbol{\mu}}_k^{(t)}=\frac{1}{\sum_{n'=1}^tw_t^{(n')}q_k^{(n')}}\sum_{n=1}^tw_t^{(n)}q_k^{(n)}\boldsymbol{x}^{(n)}\\
\hat{\Sigma}_k^{(t)}=\frac{1}{\sum_{n'=1}^tw_t^{(n')}q_k^{(n')}}\sum_{n=1}^tw_t^{(n)}q_k^{(n)}-\hat{\boldsymbol{\mu}}_k^{(t)}\hat{\boldsymbol{\mu}}_k^{(t)T}
が得られる。
混合重みのスムージング
初期値の与え方が不適切だと、1個くらいの標本しか属さないようなクラスターが出てしまい、数値的に不安定になる現象が見られる。
これを防ぐために、${\pi_k}$にゲタを履かせておくのが有用である。
\tilde{\pi}_k^{(t)}=\sum_{n=1}^tw_t^{(n)}q_k^{(n)}\\
\hat{\pi}_k^{(t)}=\frac{\tilde{\pi}_k^{(t)}+\gamma}{K\gamma+\sum_{l=1}^K\tilde{\pi}_k^{(t)}}
重みの選択と逐次更新型異常検知モデル
最終目標は、今観測したデータ$\boldsymbol{x}^{(t)}$だけを使ってモデルのパラメータを更新する式を導くことである。
逐次更新モデルの導出のために、重み係数として、
$$
w_t^{(n)}=\beta(1-\beta)^{t-n}
$$
を考える。
ここで、$0<\beta<1$は忘却率(割引率) と呼ばれる定数である。
次のような更新式が導ける。
\tilde{\pi}_k^{(t)}=(1-\beta)\tilde{\pi}_k^{(t-1)}+\beta q_k^{(t)}\\
\tilde{\boldsymbol{\mu}}_k^{(t)}=(1-\beta)\tilde{\boldsymbol{\mu}}_k^{(t-1)}+\beta q_k^{(t)}\boldsymbol{x}^{(t)}\\
\tilde{\Sigma_k^{(t)}}=(1-\beta)\tilde{\Sigma_k^{(t-1)}}+\beta q_k^{(t)}\boldsymbol{x}^{(t)}\boldsymbol{x}^{(t)T}
混合正規分布の逐次更新型EM法による異常検知のアルゴリズムを示す。
- 初期化:混合正規分布のパラメータ
$$
\Theta={\tilde{\pi}_1,\cdots,\tilde{\pi}_K,\tilde{\boldsymbol{\mu}}_1,\cdots,\tilde{\boldsymbol{\mu}}_K,\tilde{\Sigma}_1,\cdots,\tilde{\Sigma}_K}
$$に適当な初期値を設定する。
また、$q_1=\cdots=q_K=1/K$と初期化しておく。
忘却率$\beta$、異常度の閾値$a_{th}$、スムージングの定数$\gamma$を与える。
- パラメータ推定:各時刻$t$において標本$\boldsymbol{x}$を観測するたびに次の計算を行う。
- ${\tilde{\pi}_k,\tilde{\boldsymbol{\mu}}_k,\tilde{\Sigma}_k}$を次式で更新する
\tilde{\pi}_k←(1-\beta)\tilde{\pi}_k+\beta q_k\\
\tilde{\boldsymbol{\mu}}_k←(1-\beta)\tilde{\boldsymbol{\mu}}_k+\beta q_k\boldsymbol{x}\\
\tilde{\Sigma}_k←(1-\beta)\tilde{\Sigma}_k+\beta q_k\boldsymbol{x}\boldsymbol{x}^T
- モデルのパラメータ${\pi_k,\boldsymbol{\mu}_k,\Sigma_k}$を次式で求める。
\pi_k=\frac{\tilde{\pi}}{K\gamma+\sum_{l=1}^K\tilde{\pi}_l}\\
\boldsymbol{\mu}_k=\frac{\tilde{\boldsymbol{\mu}}_k}{\tilde{\pi}_k}\\
\Sigma_k=\frac{\tilde{\Sigma}_k}{\tilde{\pi}_k}-\boldsymbol{\mu}_k\boldsymbol{\mu}_k^T
- 現在のパラメータ推定値を用いて$\boldsymbol{x}$の帰属度$q_k$を次式で求める。
q_k=\frac{\pi_kN(\boldsymbol{x}|\boldsymbol{\mu}_k,\Sigma_k)}{\sum_{l=1}^K\pi_lN(\boldsymbol{x}|\boldsymbol{\mu}_l,\Sigma_l)}
- 異常判定:時刻$t$における異常度を
$$
a(\boldsymbol{x})=-\ln{\sum_{k=1}^K}\pi_kN(\boldsymbol{x}|\boldsymbol{\mu}_k,\Sigma_k)
$$により計算し、$a(\boldsymbol{x})>a_{th}$なら警報を出す。
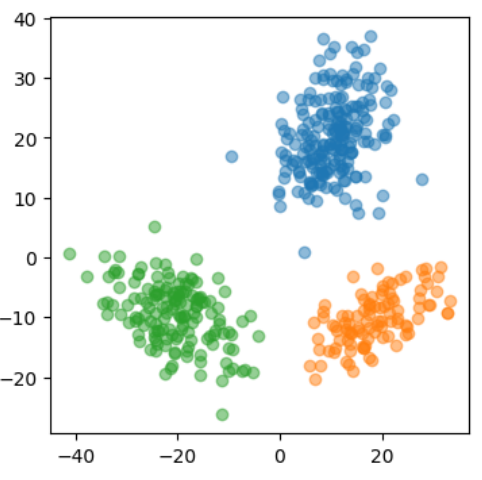
ここから実装に入る。まずはデータを準備する。
3つのガウス分布の重ね合わせを考える。
from scipy import linalg
def box_muller(n):
"""乱数の発生
"""
r1 = np.random.rand(n)
r2 = np.random.rand(n)
x = np.sqrt(-2*np.log(r1)) * np.sin(2*np.pi*r2)
return x
def sampling_gaus(n, sample, mu, sigma):
"""N次元ガウシアン分布からのサンプリング
"""
L = np.linalg.cholesky(sigma)
Y = np.array([np.dot(L, box_muller(n)) for _ in range(sample)]) + mu
return Y
# データの準備
data1 = sampling_gaus(2, 200, [10,20], [[30, 10], [10,40]])
data2 = sampling_gaus(2, 100, [20,-10], [[40, 15], [15,20]])
data3 = sampling_gaus(2, 150, [-20,-10], [[50, -20], [-20,30]])
x = np.concatenate([data1, data2, data3])
y = np.array([0]*200+[1]*100+[2]*150)
plt.figure(figsize=(4,4))
plt.scatter(data1[:,0], data1[:,1], alpha=.5);
plt.scatter(data2[:,0], data2[:,1], alpha=.5);
plt.scatter(data3[:,0], data3[:,1], alpha=.5);
#plt.xlim(-8, 8);
#plt.ylim(-8, 8);
ここで、各ステップに必要な計算を関数としてまとめる。
帰属度の計算では、multivariate_normal.pdfの共分散行列によるエラーが多発したためtry文で対処している。
あまり良い方法ではないと思われるので注意する。
from scipy.stats import multivariate_normal
def update_params(x, q, pi_tilde, mu_tilde, S_tilde, beta):
"""パラメータの更新
"""
x = x.reshape(-1,1)
pi_tilde = (1-beta)*pi_tilde + beta*q
mu_tilde = (1-beta)*mu_tilde + beta*q*np.tile(x, (K,1,1))
S_tilde = (1-beta)*S_tilde + beta*q*np.tile(x@x.T, (K,1,1))
return pi_tilde, mu_tilde, S_tilde
def calc_params(pi_tilde, mu_tilde, S_tilde, K, gamma):
"""モデルのパラメータの推定
"""
pi_new = (pi_tilde + gamma) / (K * gamma + np.sum(pi_tilde))
mu_new = mu_tilde / pi_tilde
S_new = S_tilde / pi_tilde-mu_new@mu_new.transpose(0,2,1)
return pi_new, mu_new, S_new
def calc_q(x, pi, mu, S):
"""帰属度qの計算
"""
p = np.ones((K,1,1))/K
g=1
for i in np.arange(K):
try :
g = multivariate_normal.pdf(x, mean=mu[i].ravel(), cov=S[i])
except ValueError:
# Sが半正定値でない場合
S[i,1,0] = S[i,0,1] = np.sqrt(S[i,1,1]*S[i,0,0]*1)
S[i,1,1] = np.sqrt(S[i,1,1])
S[i,0,0] = np.sqrt(S[i,0,0])
g = multivariate_normal.pdf(x, mean=mu[i].ravel(), cov=S[i])
p[i] = pi[i]*g
return p / np.sum(p)
実際に実行する。
パラメータに敏感で、上記のような対処をしてもエラーとなることが少なくない。
参考書で紹介されているアルゴリズムと違う箇所があり、帰属度を2度計算している。
$t-1$時点でのパラメータで$x_t$の帰属度$q_t$の計算を行い、最後に改めて$q_t$を計算しなおすものである。
これも計算がうまくいかなかったための対処であり、あまり参考にならないかもしれません。
K = 3 # クラスタ数
dim = 2 # 次元
T = len(x) # データ点数
arr = np.arange(T)
np.random.shuffle(arr)
# パラメータ
beta = .05
gamma = 1
# 各パラメータの初期化
# 各標本でのパラメータの値を格納できるようにしておく
q = np.ones([K, 1, 1])/K
# 初期値の設定
pi_tilde = np.ones_like(q)/K
mu_tilde = np.random.uniform(-1,1,size=(K,dim,1))
S_tilde = np.random.uniform(-3,3,size=(K,dim,dim))
S_tilde = np.triu(S_tilde)+np.triu(S_tilde).transpose(0,2,1)
S_tilde[:,0,0] = (S_tilde[:,0,0]*3)**2
S_tilde[:,1,1] = (S_tilde[:,1,1]*3)**2
pi, mu, S = calc_params(pi_tilde, mu_tilde, S_tilde, K, gamma)
# 実行
for t in np.arange(T):
xi = x[arr[t]]
q = calc_q(xi, pi, mu, S)
pi_tilde, mu_tilde, S_tilde = update_params(xi, q, pi_tilde, mu_tilde, S_tilde, beta)
pi, mu, S = calc_params(pi_tilde, mu_tilde, S_tilde, K, gamma)
q = calc_q(xi, pi, mu, S)
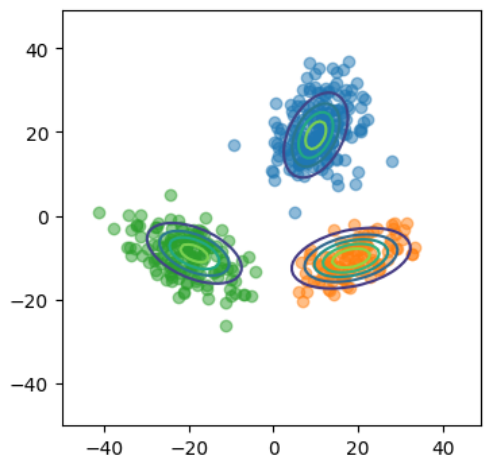
各クラスタについて別々に確率分布を見てみる。
def calc_q2(x, pi, mu, S):
"""各クラスタの確率分布
"""
p = np.zeros((K,len(x)))
for i in np.arange(K):
g = multivariate_normal.pdf(x, mean=mu[i].ravel(), cov=S[i])
p[i] = g
return p
# 可視化用のデータ
x1 = np.arange(-50,50,1)
x2 = np.arange(-50,50,1)
xx1, xx2 = np.meshgrid(x1, x2)
xx1=xx1.ravel()
xx2=xx2.ravel()
# 確率分布
P = calc_q2(np.concatenate([xx1.reshape(-1,1), xx2.reshape(-1,1)], axis=1), pi, mu, S)
# 可視化
plt.figure(figsize=(4,4))
for k in range(3):
plt.contour(xx1.reshape(len(x1),len(x1)),xx2.reshape(len(x1),len(x1)),P[k].reshape(len(x1),len(x1)),levels=5)
plt.scatter(data1[:,0], data1[:,1], alpha=.5);
plt.scatter(data2[:,0], data2[:,1], alpha=.5);
plt.scatter(data3[:,0], data3[:,1], alpha=.5);
#plt.xlim(-8, 8);
#plt.ylim(-8, 8);
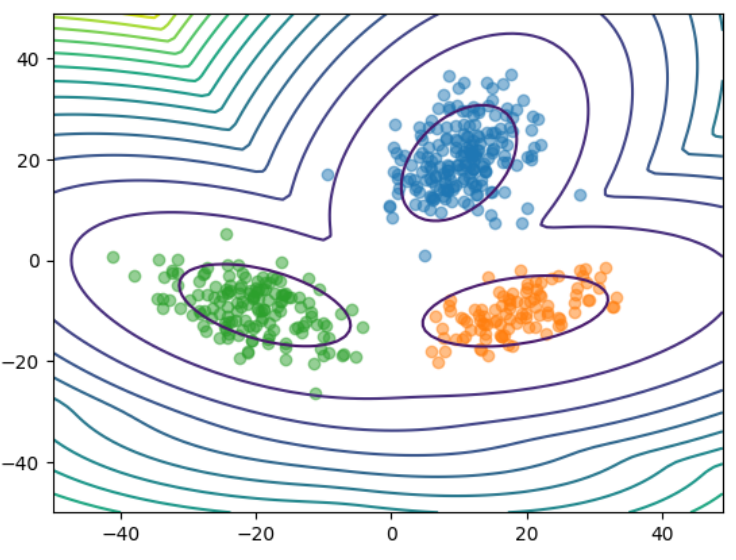
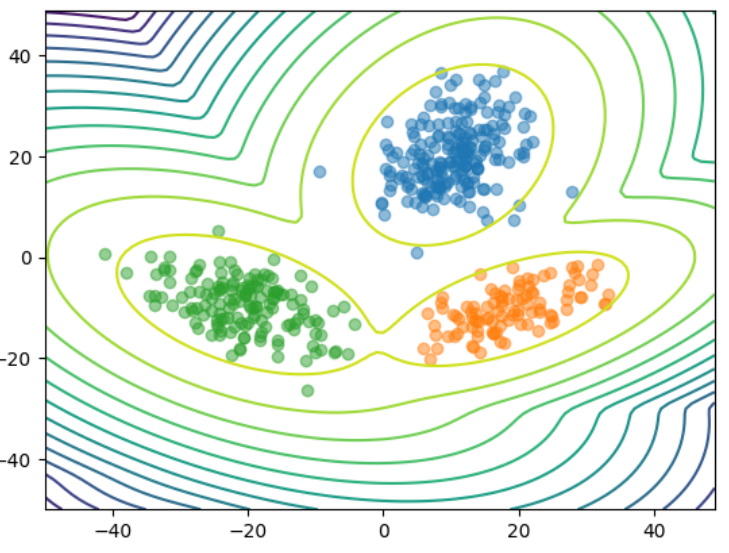
異常度の計算を行い、可視化する。
def calc_a(x, pi, mu, S):
"""異常度を計算
"""
p=0
for i in np.arange(K):
g = multivariate_normal.pdf(x, mean=mu[i].ravel(), cov=S[i])
p += g*pi[i]
a = -np.log(p)
return a
# 異常度
a = calc_a(np.concatenate([xx1.reshape(-1,1), xx2.reshape(-1,1)], axis=1), pi, mu, S)
# 可視化
plt.contour(xx1.reshape(len(x1),len(x1)),xx2.reshape(len(x1),len(x1)),a.reshape(len(x1),len(x1)), levels=15)
plt.scatter(data1[:,0], data1[:,1], alpha=.5);
plt.scatter(data2[:,0], data2[:,1], alpha=.5);
plt.scatter(data3[:,0], data3[:,1], alpha=.5);
#plt.xlim(-8, 8);
#plt.ylim(-8, 8);
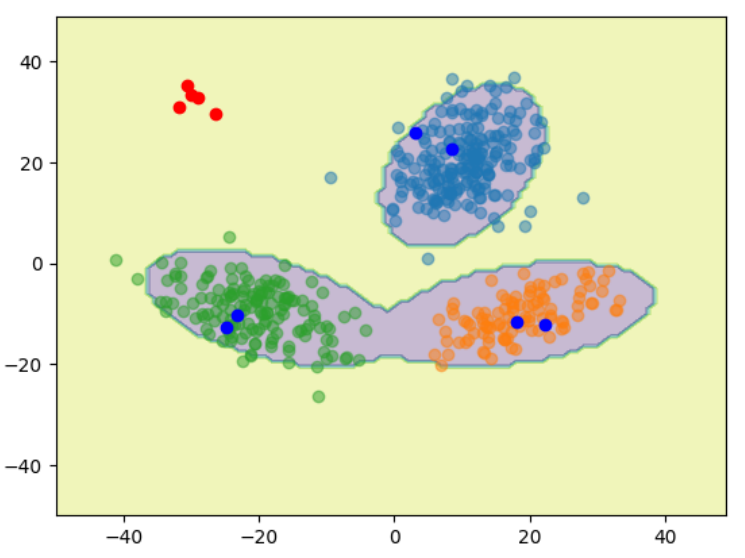
最後に異常判定の結果を可視化する。
テストデータとして元のガウス分布からサンプリングされた点と関係ない点をプロットしている。
# テストデータ
test_data1 = sampling_gaus(2, 2, [10,20], [[30, 10], [10,40]]) # 正常
test_data2 = sampling_gaus(2, 2, [20,-10], [[40, 15], [15,20]]) # 正常
test_data3 = sampling_gaus(2, 2, [-20,-10], [[50, -20], [-20,30]]) # 正常
test_data4 = sampling_gaus(2, 5, [-30,30], [[20, 1.5], [1.5,20]]) # 異常
x_test = np.concatenate([test_data1, test_data2, test_data3, test_data4])
# テストデータの異常度
a_test=calc_a(x_test, pi, mu, S)
# 異常判定
test_judge = (np.array(a_test)>10).astype(int)[0]
# 可視化用のデータ(グリッド)
a=calc_a(np.concatenate([xx1.reshape(-1,1), xx2.reshape(-1,1)], axis=1), pi, mu, S)
a_judge = (np.array(a)>10).astype(int)
# 異常判定の領域の可視化
plt.contourf(xx1.reshape(len(x1),len(x1)),xx2.reshape(len(x1),len(x1)),a_judge.reshape(len(x1), len(x1)), alpha=.3)
# テストデータのプロット
cols = ['blue', 'red']
for c in range(2):
plt.plot(x_test[test_judge==c,0],x_test[test_judge==c,1], 'o', color=cols[c])
# 訓練用データのプロット
plt.scatter(data1[:,0], data1[:,1], alpha=.5);
plt.scatter(data2[:,0], data2[:,1], alpha=.5);
plt.scatter(data3[:,0], data3[:,1], alpha=.5);
#plt.xlim(-8, 8);
#plt.ylim(-8, 8);
ガウス混合分布については、次のようにshikit-learnで実装されている。
from sklearn.mixture import GaussianMixture
gmm = GaussianMixture(
n_components=3,
).fit(x)
plt.contour(xx1.reshape(len(x1),len(x1)),xx2.reshape(len(x1),len(x1)),gmm.score_samples(np.array([xx1,xx2]).T).reshape(len(x1), len(x1)), levels=15)
plt.scatter(data1[:,0], data1[:,1], alpha=.5);
plt.scatter(data2[:,0], data2[:,1], alpha=.5);
plt.scatter(data3[:,0], data3[:,1], alpha=.5);
#plt.xlim(-8, 8);
#plt.ylim(-8, 8);
以上となります。
何か例とともに紹介しようと思いましたが、あまりにも動作が不安定なこととよい例が見つからなかったので今後の課題とします。
次回
サポートベクトルデータ記述法による異常検知