2021年3月から毎日問題が投稿されている「競プロ典型90問」も折り返し地点を越えました。
今回は53日目の問題として出題された問題に感銘を受けたので、解説記事を書こうと思います。と言っても、作問者ご自身が解説を書かれているので、本記事はその補足的な位置づけとなります。
当然のことながら問題のネタバレを含みますので、問題の挑戦を楽しみたい方は先にAtCoderの出題サイトでトライしてからお読みください(既に少なからずネタバレしているという説はありますが)
問題
一応、未挑戦者への配慮のため、問題をここに書いて行数を少し稼いでおきます。
$ $長さ$N$の非負整数列$A=(A_1,A_2,\dots,A_N)$と整数$k (1\le k\le N)$が隠されている。数列$A$は以下の条件を満たすことが分かっている。
$1\le i\le k−1$ のとき $A_i \lt A_{i+1}$
$k\le i\le N−1$ のとき $A_i \gt A_{i+1}$
整数$N$が与えられた後、あなたはクエリを何回か送ることができる。1回のクエリでは、$1\le i\le N$なる$i$を1つ指定して$A_i$の値を得ることができる。できるだけ少ない回数のクエリで数列$A$の最大値を求めよ。
$ $つまり、$k$番目が最大値で、その左右は(狭義)単調増加・(狭義)単調減少になっている数列について、なるべく少ない個数を見るだけで最大値を当てたい、という内容です。
※狭義と付けたのは、イコールなしで真に大きく(小さく)なっているという意味です。イコールがある場合は今回説明する方法は使用できませんのでご注意ください
三分探索
山型の関数や数列の探索なので、基本的には三分探索で最大値を求めることができます。
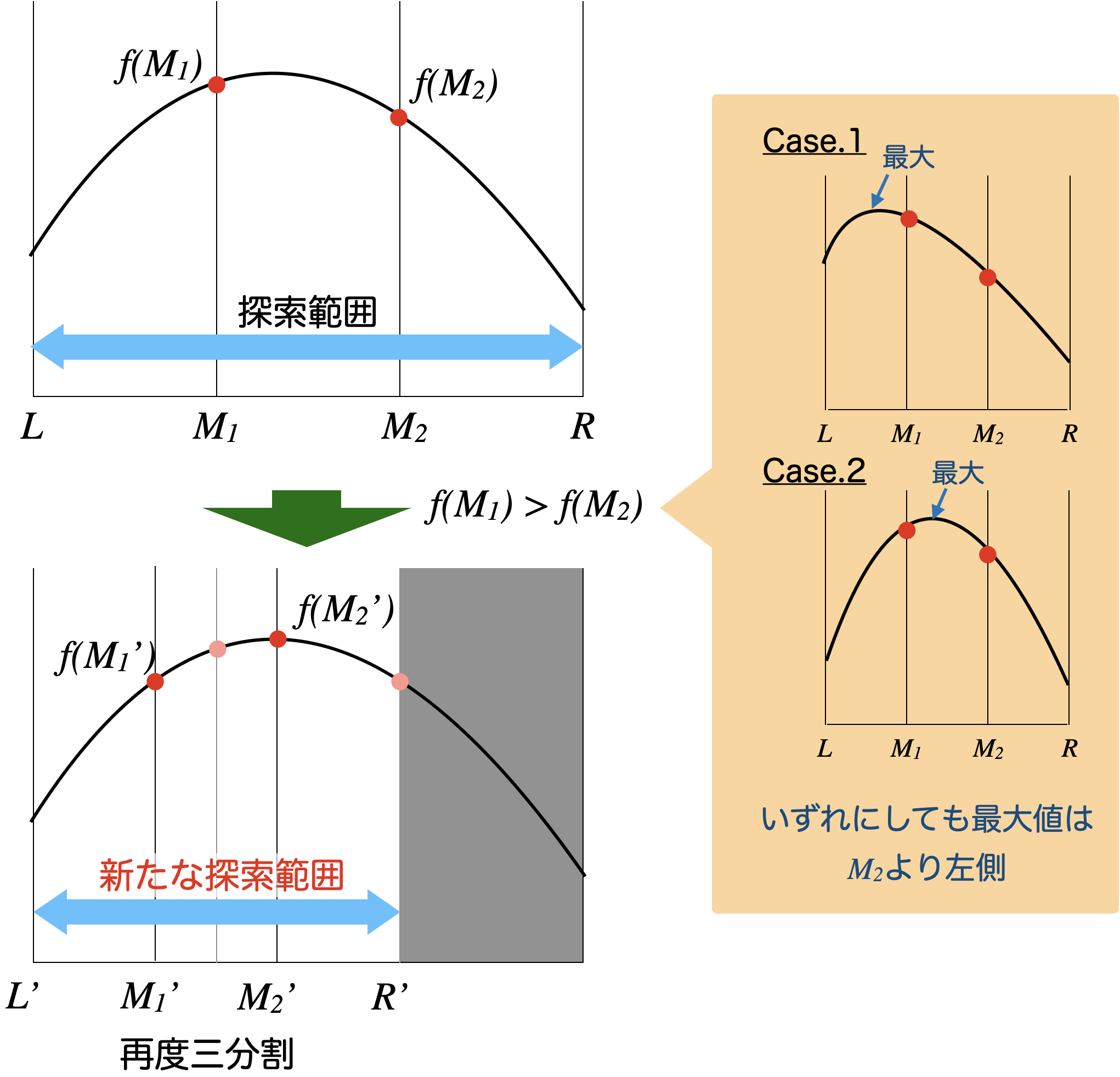
$ $下の図のように、$L$から$R$までの範囲で最大値となる点を求めたい場合、三等分点$M_1,M_2$での値を調べて、その大小を見ます。例えば$M_1$側の方が大きかった場合、右側のCase1とCase2のような状況が考えられますが、いずれにしても最大となる点は$M_2$よりは小さい側(左側)にあることがわかります。
$ $元々$M_2$だった点を$R$と取り直して、新しい探索範囲に対してまた三等分点を取って探索する、ということを繰り返していけば最大値の行き着きます。

$ $もちろん、途中で$M_1$の方が小さければ、$M_1$を$L$と取り直して新たな探索範囲を設定すれば良いです。いずれにしても1回ごとに区間が3分の2になっていきます。
ただし、「1回」と言っていますが、三等分点2箇所を調べる必要があるので、実際には2箇所調べるごとに範囲が3分の2に狭まるという挙動になります。
黄金分割探索
そこでもう少し効率の良い探索方法を考えましょう。先ほどの探索でもったいない感じがするのは、例えば1回目の探索で調べた大きい側は2回目の探索でも範囲内に残っているので、それなりの情報を持っているのに捨ててしまっている点です。
まず思いつくのは、さっき調べた点を次の三分割点の1つとして再利用する方法です。
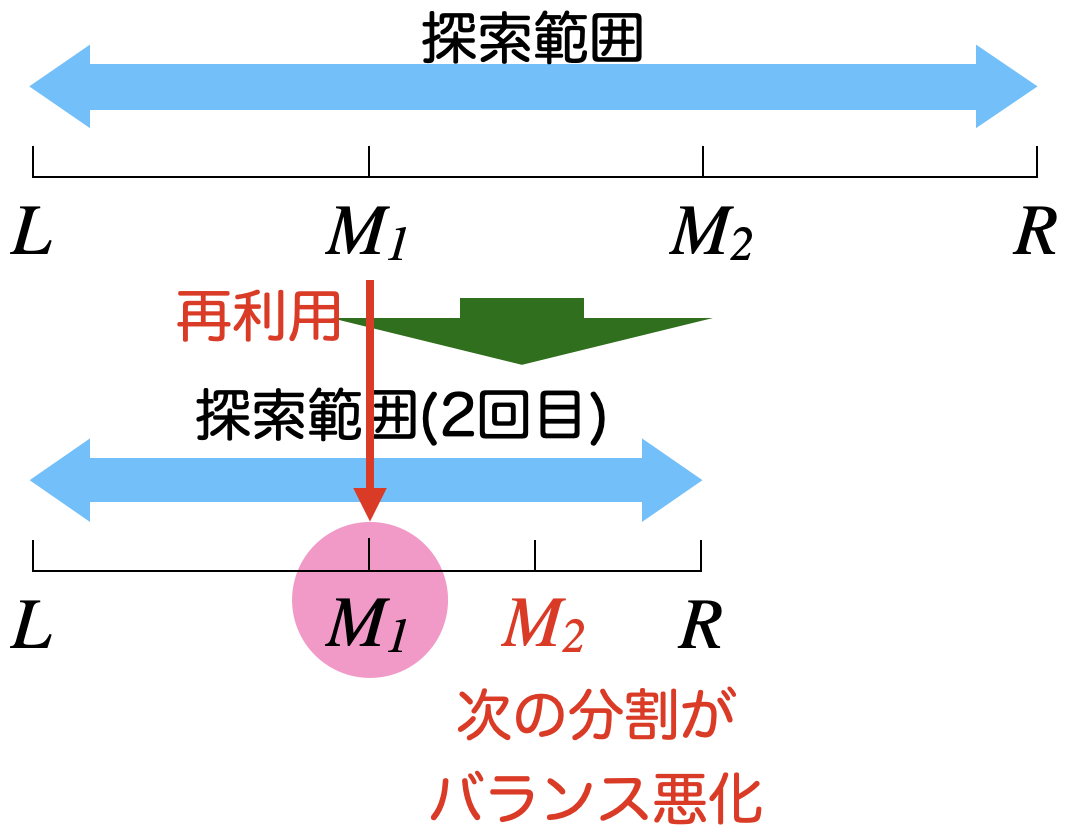
先ほどは三等分しながら探索していましたが、三分割であれば三等分ではなくても同じ理屈が成り立つので、区間が狭まった後は先ほどの点の1つは残して新たに点を1つ取れば良いのでは、と考えられます。
$ $ところが、図から見て分かる通り、$M_1$を残したとして$M_2$をどこに取ったとしても区間のバランスが悪くなってしまっています。この図の場合、次が$L$〜$M_1$側を捨てることになれば良いですが、$M_2$〜$R$側を捨てることになった場合もったいない感じです。
そこでもったいなくならないように、一定の比率を保ちながら三分割を進めて行くことを考えます。下の図のような感じです。

$ $このような点が取れれば、例えば次も$M_2$〜$R$側を捨てることになった場合、$L$〜$M_1$を同じ比率で区切ることで同じパターンを繰り返すことができそうです。
$ $比を求めたいだけなので、全体を長さ1として下の図のように置いた$x$を求めることにしましょう。
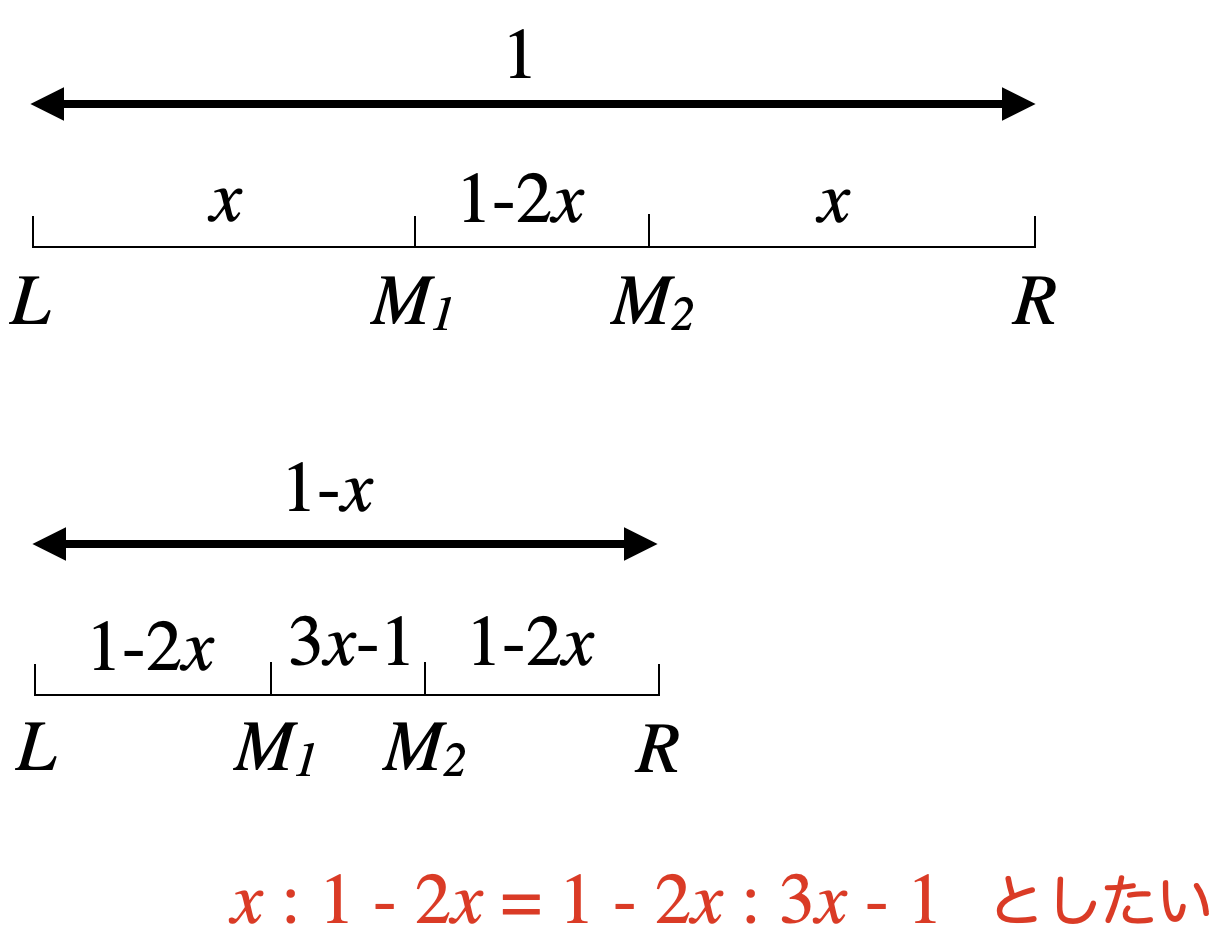
$x:1-2x=1-2x:3x-1$を解けば良いので、これは2次方程式で解くことができ、計算すると$x=(3-\sqrt{5})/2$が解となります($x=(3+\sqrt{5})/2$も式を満たしますが、長さ1の範囲に入っていません)
この比を保つように切って行くと、無限にこの操作を繰り返すことができることになります。
$ $このときの$x:1-2x$の値を計算すると$(1+\sqrt{5})/2$は黄金比となっています。これが黄金分割探索と言われる所以です。
フィボナッチ探索
さて、ここで気になるのは急に無理数が出てきてしまったことです。元々の問題では数列(つまり定義域は自然数)に対して最大値を求めようとしていました。定義域が連続である関数の最大値を調べるのであれば黄金分割探索で絞っていけそうですが、幅が整数の場合はどうすれば良いのでしょう。迂闊にやると丸め誤差が出ておかしなことになりそうです。
元々やりたかったことを落ち着いて振り返ってみましょう。

$ $幅が整数だとした場合、整数$x_i$でこんな感じに絞っていけば先ほどと同じ状況になります。この幅の関係性を見ると、$x_1=x_2+x_3$、$x_2=x_3+x_4$、…となっていて、順番は逆になっていますがフィボナッチ数列の様相を呈しています。
先ほどは何となく無限に同じことを繰り返すことを想定して比が等しくなるように分割方法を求めましたが、今我々が置かれている状況は、定義域が自然数の数列に対して実行したいので、無限に続けたいわけではありません。いつかは幅が1になって終わるはずです。
ただ初期状態の取り方がうまくないと、その状態に辿り着けずに変な形になって終わってしまいそうです。最後、どうなると我々は幸せになれるのでしょうか?
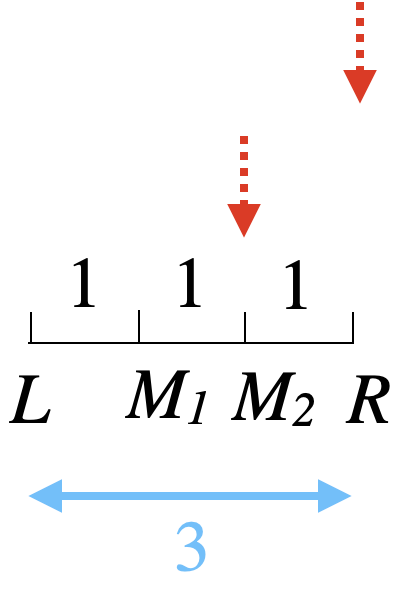
$ $最後、この形で終わることができれば、例えば$M_1\ge M_2$なら$L,M_1,M_2$のいずれかに対応する値が最大になり、いい感じです。なので、この状態に行き着くように区間の絞り方を逆算していってみましょう。

3,5,8,13,...と、まさにフィボナッチ数列が見えてきました。このようにフィボナッチ数を起点とすれば、前の項を分割点として三分探索を行っていくことで、最後は理想型で終えることができるようになります。
よく知られているように、フィボナッチ数列の隣接2項の比は黄金比に収束しますから、この探索方式も黄金分割探索とほぼ同じことをしていることになります。
さらに幸せになるために
ここで気になることが2つあります。初期状態がフィボナッチ数の幅だったら先ほどの方式でうまく行きますが、もし違ったらどうすれば良いでしょうか?
$ $もう1つ気になることとして、三分探索では$M_1$や$M_2$を調べて大小関係を比較し、小さい側のサイドを捨てるということを繰り返しています。最終形にたどり着いたとき、先ほどの図で最後に$M_1$を調べて終わりますが、このときに$L$や$R$は必ずしも調べているとは限りません。ここまで頑張って効率化してきたのに、最後に$L$や$R$の値を調べるのも何か野暮な感じがします。
$ $これらを一気に解消するのが両サイドにダミーの領域を置く方式です。元々調べたい領域が$1,2,\dots,N$だったとして、左側に$0$を、右側に最後がフィボナッチ数となるように1個以上のダミー領域を持たせた範囲に拡張します。今回の元々の問題の場合、数列の値は0以上であることが与えられていますから、$A_0=-1$、$A_{N+1}=-1,A_{N+2}=-2,\dots$のようにみなしておくことで、絶対に最大値になることはないように区間を拡張することが可能です。
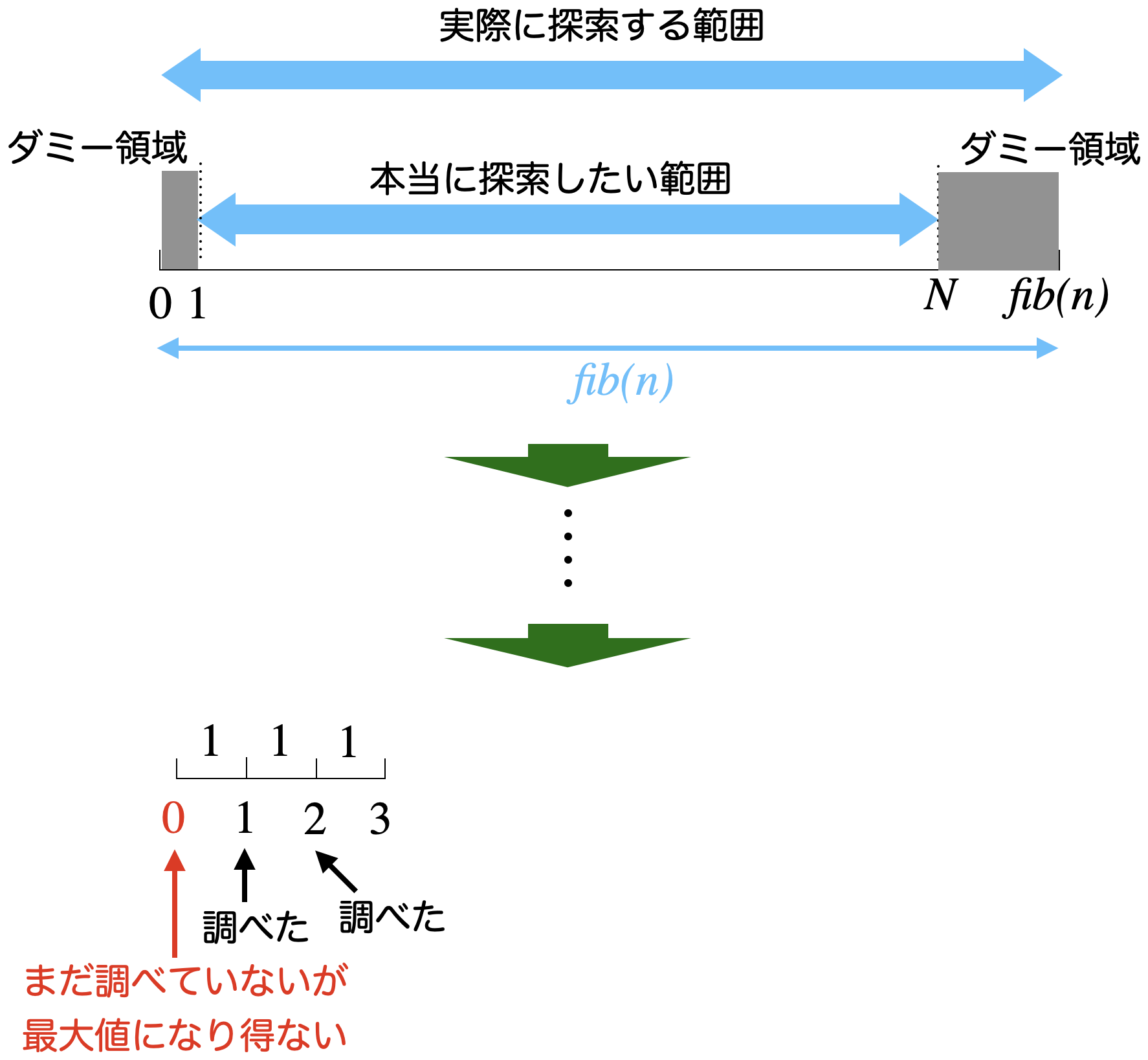
これでフィボナッチ探索を行うと(既に値を知っているダミー領域が分割点になった場合は調べなくて良い)、最終的に理想形に行き着いた上、最後に残る3点は既に調べている点であるかダミー領域であるかのどちらかなので、最後に値を調べることを余計にしなくて良くなり、更に幸せになれます。
以上、三分探索、黄金分割探索、フィボナッチ探索について説明してきました。何かのお役に立つと幸いです。