概要
本記事では、プログラミング言語で配列の生成・初期化コストを低減する方法について説明します。言語はJavaで説明しますが、他の言語でも考え方は通用すると思います。
タイトル詐欺的なところがあるかもしれないので予めお断りしておきますと、基本的には一度作った配列を使い回すという至極当たり前な方法なのですが、使い回す際の工夫によって、初期値を配列全体に設定するコストを低減することができる、という内容になります。
モチベーション
競技プログラミングなどで最短経路問題を解く時に、ダイクストラ法や01BFS等を使うために各頂点までの距離を保持する用の配列を用意することがあると思います。以下のようなコードでdistに当たる変数です。
int[] dist = new int[N];
Arrays.fill(dist, Integer.MAX_VALUE);
dist[0] = 0;
ArrayDeque<Integer> queue = new ArrayDeque<>();
queue.add(0);
while ( queue.size() > 0 ) {
// 省略
}
$N$が頂点数ですが、配列distの生成と初期値(ここではInteger.MAX_VALUE)を代入するのに$O(N)$の計算量がかかります。ただしこの場合は、全体の計算量がダイクストラだったら$O(M + N\log N)$、01BFSなら$O(M + N)$かかるので、配列の初期化は特にボトルネックになるようなものではありません。
ところが、ヒューリスティックコンテスト等では、探索する盤面全体としてはそれなりの広さがあるものの距離や経路を求めたい箇所はその中の一部の領域だけで、配列の生成・初期化の部分がボトルネックになってしまうというケースがあります。
例として、先日行われた第一回マスターズ選手権予選で、北村氏による解法では、現在地から最も近い「配置条件を満たしていないマス」およびそこまでの経路を求める必要が出てきます。盤面全体の広さとしては$N\times N$ですが、「配置条件を満たしていないマス」はすぐ近くにあることが期待できるので、毎回distに当たる変数の初期化を行うと、そこがボトルネックになってしまいます。
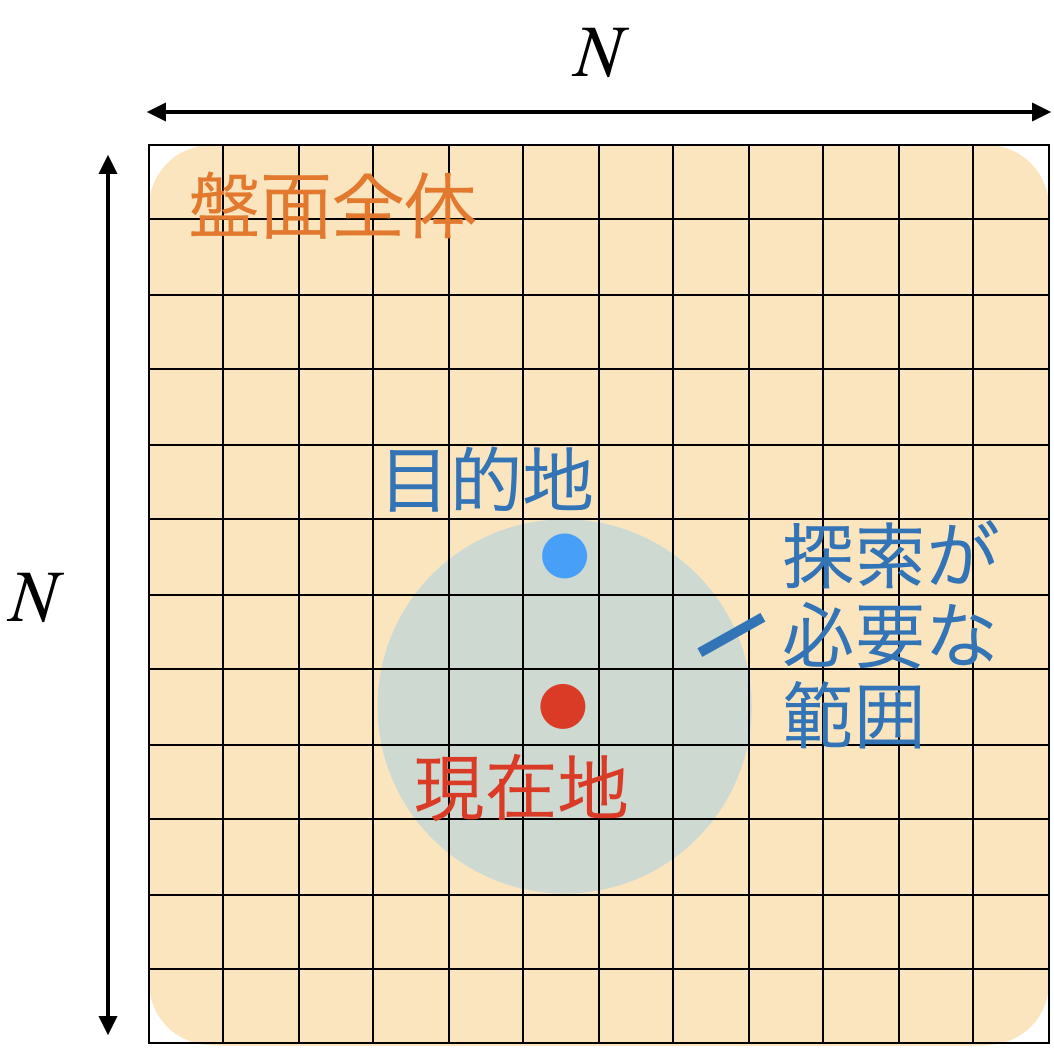
本記事では、このような状況で初期化を$O(1)$で実行するテクニックについて説明します。
もちろん、連想配列(JavaではHashMap)を使うことで解決する方法もありますが、Javaの場合だとオートボクシングが発生してパフォーマンスが劣化しがちなので、別の方法を考えてみました。
解決方法
以下のアプローチです。
- 値を保持する配列に加えて、世代番号を保持する配列を持つ。現在世代番号も管理する。
- 値を設定する場合は、値を保持する配列の更新に加えて、世代番号の配列も現在世代番号に更新する。
- 値を取得する場合は、世代番号が現在世代番号であれば値そのものを返し、違う場合は初期値を返す。
- 初期化を行う場合は、現在世代番号を1つ進める。
ソースコードにすると以下のようになります。
class MyArray {
int N = 0; // 配列サイズ
int[] val = null; // 値を保持する配列
int[] gen = null; // 世代番号を保持する配列
int curGen = 1; // 現在世代番号
int defaultVal = 0; // 初期値
MyArray(int N, int defaultVal) {
this.N = N;
this.val = new int[N];
this.gen = new int[N];
this.defaultVal = defaultVal;
}
// 初期化
void clear() {
curGen++; // 現在世代番号をインクリメント
}
// 値の取得
int get(int i) {
return gen[i] == curGen ? val[i] : defaultVal; // 世代番号が一致しない場合は初期値を返却
}
// 値の設定
void set(int i, int v) {
gen[i] = curGen; // 現在世代番号を設定
val[i] = v;
}
}
clear()を実行してもvalの中身はそのままですが、現在世代番号をインクリメントすることで$O(1)$で実質的に各要素を初期値扱いにしています。メリットはもちろん初期化が配列の長さに依存せずに実行できることですが、デメリットもあります。
- 値の設定時に2つの配列を更新する分パフォーマンスが落ちる
- 値の取得時に条件分岐が発生する分パフォーマンスが落ちる
したがって、「モチベーション」の項で述べたように、配列の一部だけを使って処理を行うような場合は高速化が図れますが、配列全体を使うようなケースの場合はかえって劣化することになります。
おわりに
競技プログラミングでもアルゴリズム系のコンテストでこのテクニックを使うことはほぼないと思いますが、ヒューリスティックコンテストでは全体の一部だけしか使わない判定を繰り返し実施することがあるので、これまでのコンテストで筆者は何度かこのテクニックを使用しています。
もっと良いやり方があるのか理由は不明ですが、あまりネット上で見かけないテクニックだったので、今回記事にしてみました。何かの参考になれば幸いです。
〜追記〜
Xで情報をいただきましたが、昔、コンピュータ将棋で置換表を初期化するのにもこの手法が使用されていたそうで「論理初期化」と呼ばれていたそうです。
(さらに追記)
追加情報をいただきました。PsyhoさんによるヒューリスティックコンテストのTips集によると、この手法は"Fast-Clearing Array"と呼ばれているようです。
- Psyhoさんによるヒューリスティック・ボットコンテストのための無料Tips (Tipsを翻訳された方の記事。#63,64参照)
また、上記記事からリンクされていますが、tomerunさんの記事でもこの手法の紹介がありました。こちらでは固有の名称では呼ばれておらず、以下記事タイトルの通りとなっています。