はじめに
オセロアドベントカレンダー2020も残り1週間となりました。
3日目の記事「【withコロナ】超リアルな対局サイトをビデオ通話付きで実現する」で斜めから盤を見たときの石の座標の計算が雑なままとなっていました。本記事では、この計算をきちんとやってみたいと思います。
なお、タイトルの元ネタはフレーズだけ聞いたことがあるものの何なのか全く知らなかったので、ググってみたところテレビドラマだったようですね。上から見たときについては特に書くべきことはないと思いますので、斜めから見たときの話だけをすることにします。
盤面を斜め上から見る
盤面を斜め上から見たいのですが、色々と計算が大変です。そこで少しでも計算の労力を減らすため、斜め上から見るのでなく、真上から見て盤面を傾けるというアプローチで計算したいと思います。
具体的には以下のような座標と盤で考えましょう。

xy平面上にあった盤面を、x軸を回転軸として角度$\theta$だけ傾けます。
すると、盤面上の点$(p,q,0)$は以下の点に移動することになります。
$$(p,q\cos\theta,-q\sin\theta)$$
視点を$(0,0,a)$、投影面をxy平面とすると、上記の点と視点を結んだ線分とxy平面の交点を求めれば良いことになります。下の図はyz平面です。

計算はちょっとややこしいですが、直線の方程式なので地道に計算すると、求める投影面上の点は以下のようになります。
$$\left(\displaystyle\frac{ap}{a+q\sin\theta},\frac{aq\cos\theta}{a+q\sin\theta},0\right)$$
pとqそれぞれ-4から4までが盤面上の格子点になります。これで「【withコロナ】超リアルな対局サイトをビデオ通話付きで実現する」の記事で懸案となっていた石の座標の求め方がわかりました。
描いてみる
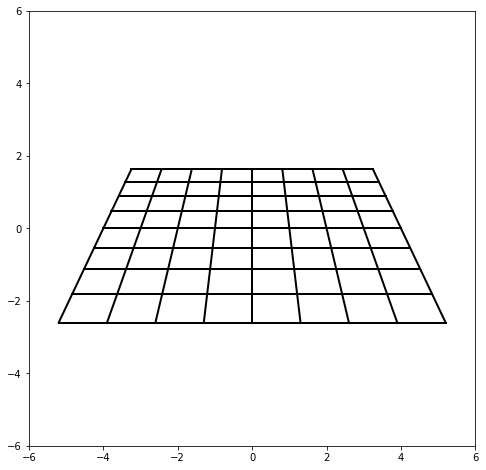
pとqを-4から4まで動かしてみると盤面を描くことができます。pythonのmatplotlibで描いてみました。aとth($\theta$)の値を変えると視点や角度を変えることができます。
import math
import matplotlib.pyplot as plt
a = 15
th = 60 / 360 * 2 * math.pi
# 元の点(p,q)に対応する投影面上の点を求める
def projection(p, q):
return a * p / (a + q * math.sin(th)), a * q * math.cos(th) / (a + q * math.sin(th))
plt.figure(figsize=(8, 8))
plt.xlim(-6, 6)
plt.ylim(-6, 6)
for i in range(-4, 5):
# 縦方向の線
x0, y0 = projection(i, -4)
x1, y1 = projection(i, 4)
plt.plot([x0, x1], [y0, y1], 'k-', lw = 2)
# 横方向の線
x2, y2 = projection(-4, i)
x3, y3 = projection(4, i)
plt.plot([x2, x3], [y2, y3], 'k-', lw = 2)
plt.show()
奥の方から手前にかけて段々線の間隔が広がっていることに注意してください。
石の問題
「【withコロナ】超リアルな対局サイトをビデオ通話付きで実現する」の記事では、石はPOV-Rayで作成した画像で用意したので特に問題なかったのですが、石の円が斜めからみるとどうなるかも気になります。
これについても計算してみようと思ったのですが、実はこれはかなり難しい問題であることがわかりました。結果的には楕円になるのですが、長軸と短軸が少し傾いていたりなど、一筋縄ではいきません。
円を投影したときの話については、パースフリークスというサイトに記事がありましたので、興味のある方は読んでみてください。
おわりに
今回の記事はこれで終わりです。一応pythonの描画用ソースコードを入れてそれっぽくはしてみましたが、ほぼ数学の記事になってしまいました。
今年のオセロアドベントカレンダーの私の記事はこれまでとなります。あと1週間、どんな記事が公開されるか楽しみですね。では良いお年を!