はじめに

HACK TO THE FUTURE 2023予選(AHC016))に参加し、最終テストで相対スコア1.1T点で28位を獲得しました。
終了後流れてくる情報を見ると、割と解き方のバリエーションが多かったようで、筆者も書き残しておこうと思います。

問題概要

今回はGraphoreanというグラフを送ることができるタイムマシンの問題です。概要としてはM種類のグラフがタイムマシンで送られて来るのですが、送信過程で辺の有無に一定のノイズが入るのと、頂点は識別できなくなってしまいます。送られてきたグラフが元々どのグラフだったかを当てる問題です。手順としては以下の通りです。

まず、コンテスタントは、送りたいグラフの種類数M(10〜100)と、エラー率ε(0.00〜0.40)が与えられる
コンテスタントは(都合が良いように)グラフの頂点数N(4〜100)と、M種類のN頂点無向グラフを決め、ジャッジに送る
ジャッジは、M種類のグラフのうち1つを選び、辺の有無を確率εで反転し、かつ頂点をシャッフルし、コンテスタントに送る
コンテスタントは送られてきたグラフが、元々どのグラフだったかを当てる
3.と4.を100回繰り返す

判定誤り数が少なく、Nが小さいほど高得点となります。
詳細はリンク先を参照してください。

解法

方針

Mとεで場合分けして解きました。4種類に場合分けしています。3個目は2個目の発展系なので、大まかには3種類の場合分けです。

一般的な場合
- 頂点を3グループに分けて、グループ内の頂点を全部結合し(クリーク)、各グループの頂点数の組で情報を伝達する
ε = 0の場合
- N=4,5,6のグラフで、頂点の入れ替えで重なるものは同一視した場合に、異なる種類のグラフを選んでおき、送られてきたグラフがどれかを判定する
ε ≠ 0だが、εが小さい場合
- N=6,7のグラフで、頂点の入れ替えで重なるものは同一視した場合に、多少辺の有無が変わっても復元できるように元のグラフを選んでおき、送られてきたグラフがどれかを判定する
εもMも大きい場合
- 当たらないので、諦めてN=4のグラフを送り、運を天に任せる

一般的な場合(クリークサイズで伝達)

伝達方法

伝達中に確率εで辺の有無が変わってしまうので、細かい情報は失われてしまうと考え、多少情報が失われても伝わりそうなものが何かないかと考えました。その結果、ある程度の規模の頂点をグループ化して相互に全結合しておけば、多少ノイズが入ってもサイズは分かるのではないかという発想となりました。

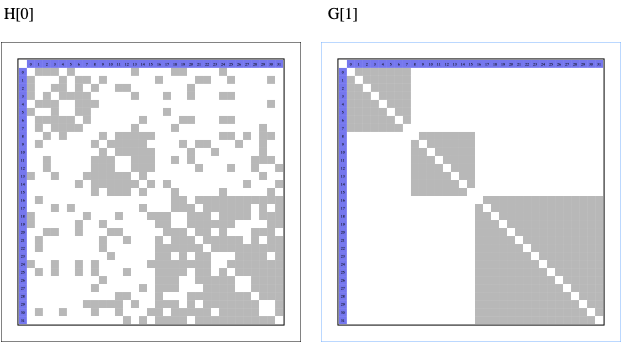
このように頂点を3グループに分けて、各グループは相互に全結合しておきます。このグループサイズの組み合わせ（この図の場合はN=32で、ブロックサイズは[8,8,16]）で伝達を試みます。
Nを決めると、2つのサイズを決めた時に残りのサイズは決まるので、サイズの種類数はおよそ2乗のオーダで増えていきます。Mが100種類程度であれば十分な量の組み合わせが作れます。

復元方法

どの頂点がどのグループに属するかをランダムで振り、そのグループが正しいとした場合のノイズが入った回数を評価値として、山登りをしました。状態遷移は1頂点を別のグループに移すという遷移で、局所解にたどり着いたら一部をランダムにシャッフルしてやり直し、最も評価値の良かったもの(ノイズが少ないもの)を採用しました。

これにより各グループに所属する頂点数がわかるので、元々のどのグラフだったかがわかることになります。

さて、ここまでを実装した結果、当然ではありますがεが大きくなったときに正解率が下がっていきました。ここでの疑問は、正解率が下がっているのは

山登りで実装している復元の精度の問題
ノイズ量の問題(サイズとノイズ率のバランスが悪く、復元が完璧だったとしてもサイズを取り違えてしまう)

のどちらなのかということです。前者であれば焼きなまし等のもう少し高度な推定をしようと思ったのですが、実験してみるとどうやら後者の要素の方が大きいことがわかりました。そこでここからノイズをどう扱っていくかが求められることになりました。

ノイズ対策

εが大きくなってくると、例えば[3,5,10]だったブロックが[4,4,10]に取り違えられてしまうというようなことは容易に発生します。直感的にはサイズの小さいブロックは取り違えられる確率が高い気がしたので、εに応じて最小ブロックサイズを一定以上にする、というのを取り入れました。最小ブロックサイズを大きくすることで必要なNの値は大きくなってしまいますが、誤答数が減ることでスコアアップにつながるだろうという考え方です。
これはある程度うまく行きました。

しかし、上位陣のスコアを見るにこれだけでは太刀打ちできませんでした。
必要と思われるのは、ブロックのサイズ組毎にどの程度ブレるかを見積もり、その幅程度が重ならないように使用するサイズ組を選定する、ということです。これがうまくできると、

サイズの大きいブロックがブレてもある程度吸収できる
サイズの小さいブロックを使っていない分の無駄を減らせる

ということで、二重の効果が見込めます。

ただ3つのサイズの組のブレ幅を直接見積もるのは難しかったので、2ブロックの場合のサイズ組がεやサイズによってどの程度変動するかを見積もり、3ブロックの場合は2ブロックの組み合わせ3パターンでブレの度合いが決まると仮定して見積もることにしました。
細かいところは到底記事に書ききれないほど大変なことになってしまいましたが、大まかには以下のようなことをしました。

2ブロックのサイズ組とε毎に、小さいブロックのサイズ差分(サイズがどれだけ増えたか)の平均と分散をシミュレーションで測定
合計サイズとεを固定すると、サイズ差分が2ブロックのサイズの差におおよそ比例していることがわかり、その係数を求める
その係数が合計サイズとεから導出できないか色々と頑張る

兎にも角にも、精度がどの程度かはともかくとして、2ブロック間でのサイズの変化を大まかに見積もることができ、これを利用してサイズのブレ幅の標準偏差に比例した幅を持たせながら、使用するサイズ組を決めることにしました。
これである程度改善することができました。

この他の工夫として、Mとε毎に最適なサイズNを実験により事前計算しようとしましたが、誤差幅の組み込みができたのが最終日前日で、計算が間に合わなそうだったので断念しました。
ただ1日余裕があったので、Mが10個間隔で実験し、間は適当に補完しました。

ε=0の場合(同型グラフで伝達)

ε=0の場合はノイズが入らないので、頂点が入れ替わることを除けば全ての情報が伝達されることになります。つまり、頂点の入れ替えで同じになるグラフを同一視し、その代表グラフを選定し、また任意に与えられたグラフがどの代表グラフかを判定できれば完全に解くことができます。

例えばN=4のグラフは頂点の入れ替えで重なるグラフを同一視すると以下の11種類になります。

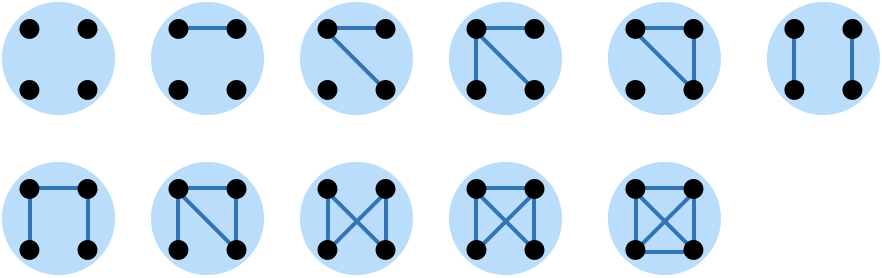
つまりM=10,11の場合はN=4で解くことができます。
これはABCで過去に出題された問題Graph Isomorphismの類題で、N!通り試せば判定することができます。

同様にNを大きくすると、N=5で34パターン、N=6で156パターンあることがわかり、ε=0の場合は、M=100でもN=6で足りることがわかります。

ε ≠ 0だが、εが小さい場合(余裕を持たせた同型グラフで伝達)

εが0ではないけれども十分小さい場合、ノイズで辺が入れ替わっても1本程度だろうという前提で幅を持たせて解くことができます。
先ほどのグラフ自体を頂点とみなし、辺1つの変化で移り変わるグラフ同士を線でつないでみます。

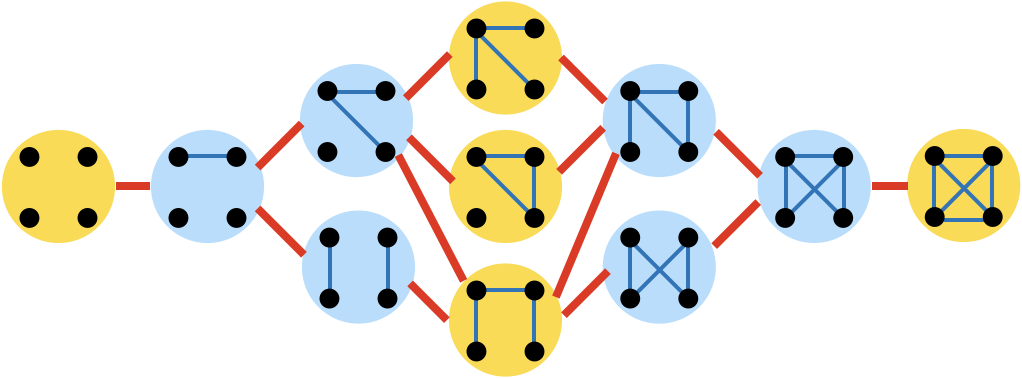
ここで、黄色いグラフを選ぶと、これらは相互に距離2以上離れているので、1つの辺の変化では移ることがありません。従って、黄色いグラフをあらかじめ選定し、水色のグラフが来た場合は隣接する黄色いグラフを回答するようにすれば、辺のノイズが1個までであれば復元できることになります。
N=4だと黄色いグラフは5個までしか選べませんでしたが、例えばN=7にすると、グラフ自体は1044種類ありますが、少なくとも73個のグラフを互いに距離2離すように選ぶことができます(もしかしたらもっと多く選べるかもしれません)

基本的にはεが小さい場合はこのようなやり方で解きましたが、以下補足です。

相互距離が奇数の場合でも、「水色」のグラフが与えられた場合に最も確率の高い「黄色」のグラフ(2個の辺の変化で到達するパターンの最も多いグラフ)にすることで、相互距離が1小さい偶数のグラフよりも正解精度を上げることができる
相互距離は統一されていなくても良いので、途中まで距離2、途中から距離1で構成する、というようなことで詰め込むこともできる
頑張れば効率の良い選定パターンを事前計算しておくこともできるかもしれないが、時間がなく手が回らず
N=8も頑張ればできたかもしれないが、時間がなく手が回らず
一般方式(クリークサイズ方式)とどちらを採用するかは、事前シミュレーションで期待スコアの高そうな方を選定
- ε=0.01は全Mでこの方式を採用
- ε=0.02〜0.04はMがある程度の大きさまではこの方式を採用。Mが大きい場合は一般方式を採用
- ε=0.05以上は全面的に一般方式を採用

εもMも大きい場合(運任せ方式)

今回のスコア計算式を見ると、N=100で頑張った結果正解率が30%にも満たないような場合は、N=4でランダムに回答した方がスコアが高くなることがわかります。
εもMも大きい場合は、この方法に頼ることにしました。ささやかな頑張りとして、N=4で辺が1本もないパターンをM/2個と全結合をM/2個の2パターンを作り、どちらっぽいかを多数決で判定した後にあとはその中の1つを回答する方式としました。

一般方式改善前は、ε=0.36以上は完全にこの方式でしたが、一般方式改善後はε=0.36は一般方式に、ε=0.37以上でもMが小さい場合は一般方式の方が良いことがわかり、結果この方式に頼ったのはεもMも大きい場合だけになりました。

おわりに

今回、これ以上のアイディアが思いつかなかったので、一般方式の誤差の評価に最も時間を注ぎ込みました。かなり苦労をしてそれなりに効果はあったのですが、改善効果に限界があり、上位陣との間には大きな壁を感じました。
上位の方の中には、クリーク自体を頂点として辺でつないで伝達するというようなやり方をやっていたようで、なるほどと思いました。

今回は順位の決定方式も相対スコア方式となり、絶対スコアが小さくなりがちなεが大きいケースについても頑張る価値があることになり、力を入れる場所も最終結果に影響を与えたのではないかと思っています。
頑張り甲斐のある楽しい問題で、問題制作者や運営の方々、どうもありがとうございました。参加された方々もおつかれさまでした！

HACK TO THE FUTURE2023予選(AHC016)解法