概要
$\hspace{1em}$ 配列要素を総和処理するときのアルゴリズムとして提案したピラミッド方式は、Google Apps Script（GAS）ではその効果が顕著に現れました。そこで、他の言語でもその効果はあるのかどうか、適応性について気になりましたのでGASの他にいくつか言語を選択して検証を行いました。結果として配列要素の総和処理に対してピラミッド方式はGAS以外にも効果が認められました。ただし、効果が認められるためには条件が必要であることが分かりました。スクリプト実行時に総和処理に対して最適化が行われる場合、ピラミッド方式の効果は認められず、従来法の方が処理速度が速くなることが分かりました。一方、最適化が行われない場合は明確な効果が現れました。これらの結果を用いてピラミッド方式が適応できるものとそうでないものを区別することができました。また、この結果を用いて最適化の視覚化についての可能性も議論しています。
データの取得方法
$\hspace{1em}$ 記事内で使用している$\Psi$, $\mu$, $\theta$, $\phi$, $\omega$は、それぞれスクリプト実行中の総データ量(byte)、配列の各要素のデータサイズ(byte)、配列の要素数、分割サイズ(byte)、段階数を意味します。詳細はこちらで確認することができます。データ取得で使用するサンプル配列は、2次元配列で各要素は2要素を持つ1次元配列です。[['0000000', 'a'], ['0000001', 'a'], ['0000002', 'a'], ,,,] のようになっています。文字列8バイトに区切りの','、改行コード'\n'を合わせて10バイトになります。$\omega$と$\phi$についてはそれぞれの$\theta$に対して最適な値（ $\omega=\log_{10} \theta - 1$, $\phi=10$）を使用しています。[1] GAS以外の言語として、下記表1にあるような6つの言語を選択しました。c++についてはg++でコンパイルし、コンパイル時は'-O2'のオプションを付けています。これらの中にはコンパイルされるものや総和処理に対して"+"オペレータ以外に専用のメソッドを持っている言語もあります。ピラミッド方式に対するリファレンスとして従来法を使用した結果も同時に掲載しています。測定に使用した計算機のスペックはCPU Core i5-3210M, Memory 8GB, OS Windows10 (x64) (v1607)です。
表 1: データ取得に使用した言語.
| Language | Version |
|---|---|
| c++ | Compiler g++ (6.1.0 on msys2) |
| Go | v1.7.1 windows/amd64 |
| Java | v8 (1.8.0_101) |
| Javascript on Node.js | v6.3.0 (v8 '5.0.71.52') |
| Python | v3.5.2 |
| Ruby | v2.3.1p112 |
ピラミッド方式のGAS以外への効果
Fig. 1: g++ using "+"
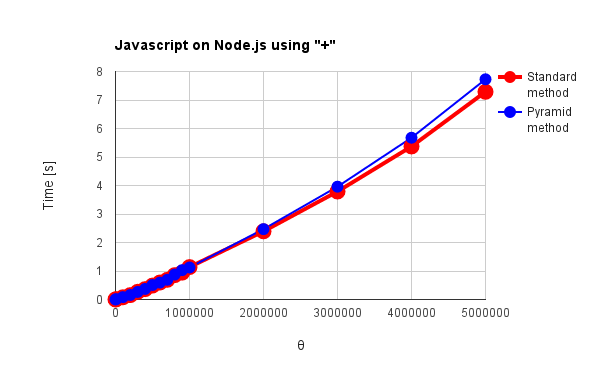
Fig. 2: Javascript on Node.js using "+"
Fig. 3: Python using "+"
Fig. 4(a): Go using "+"
Fig. 4(b): Go using "[]byte"
Fig. 4(c): Go using "[]byte"
Fig. 5(a): Java using "+"
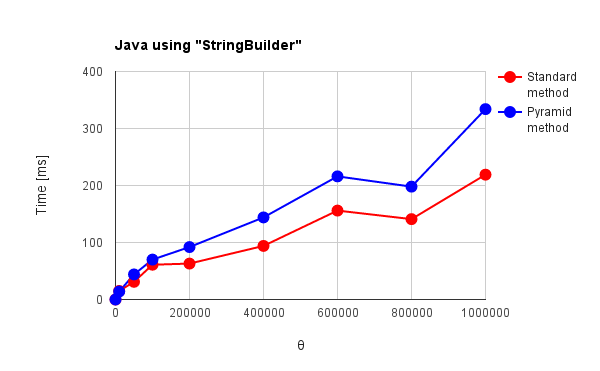
Fig. 5(b): Java using "StringBuilder"
Fig. 6(a): Ruby using "+"
Fig. 6(b): Ruby using "<<"
図1, 2, 3, 4(a), 5(a), 6(a)は"+"オペレータを使用した際の結果、図4(b)(c), 5(b), 6(b)は言語が独自に持っている総和処理専用のオペレータあるいはメソッドを使用した際の結果です。また、図1 - 図6は、赤色線がこれまでの手法（順次加算方式）、青色線がピラミッド方式による結果です。これらの結果から分かることは次の通りです。
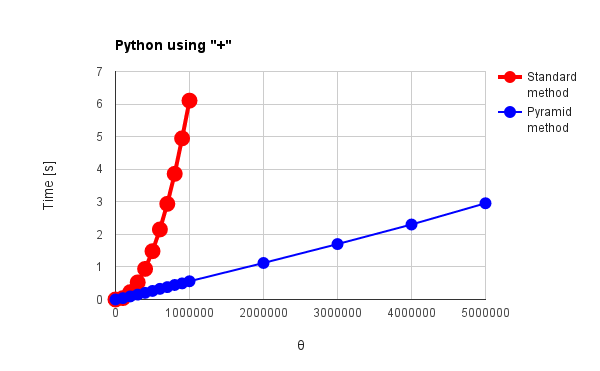
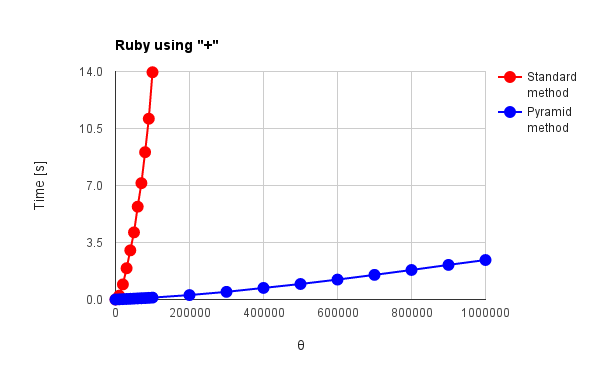
- "+"オペレータを使用して得た図3, 図6(a)のPython, Rubyの結果はピラミッド方式の効果が顕著に現れている。
→ 理論で得た結果（従来法では総和処理中に動く総データ量$\Psi$は$\theta$の2乗に比例して増加。ピラミッド方式では総和処理中に動く総データ量$\Psi$は$\theta$の線形比例で増加。）と傾向が同じ。
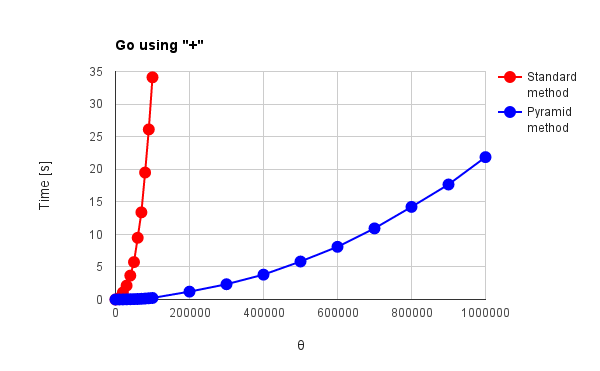
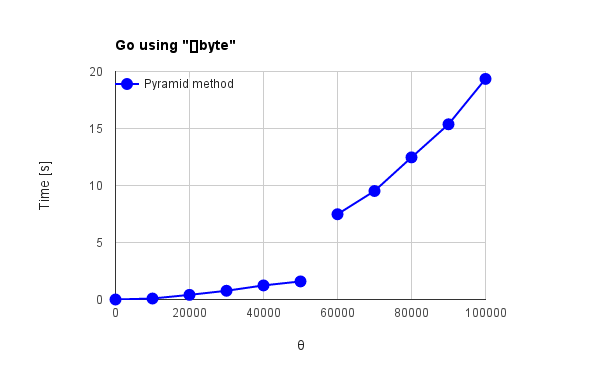
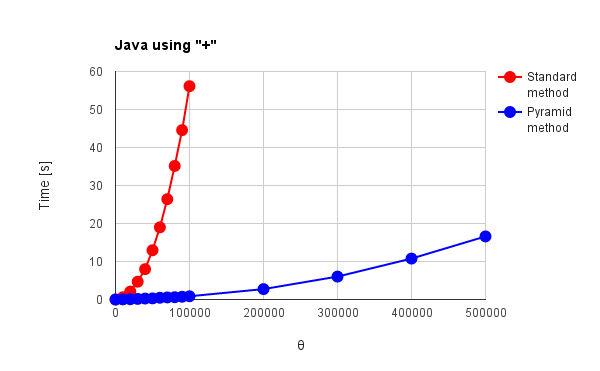
- "+"オペレータを使用して得た図4(a), 図5(a)のGo, Javaの結果は従来法、ピラミッド方式共に$\theta$の2乗に比例して処理時間が増加している。理論のピラミッド方式では$\theta$の線形比例で処理時間が増加することと異なる。
→ 最適化が影響している可能性。
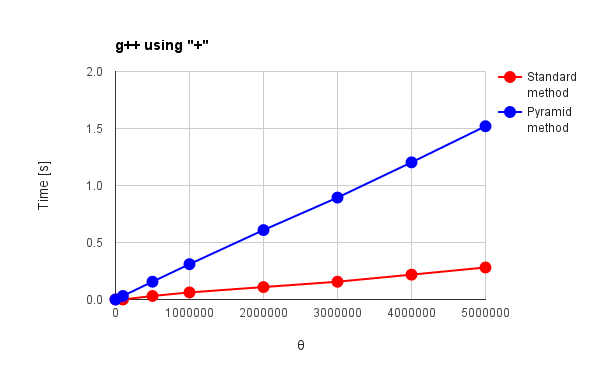
- "+"オペレータを使用して得た図1のg++の結果はピラミッド方式の方が従来法よりも処理時間が長くなっている。
→ 最適化が影響している可能性。ピラミッド方式の方が従来法よりも遅い理由についての検討は下に記載。
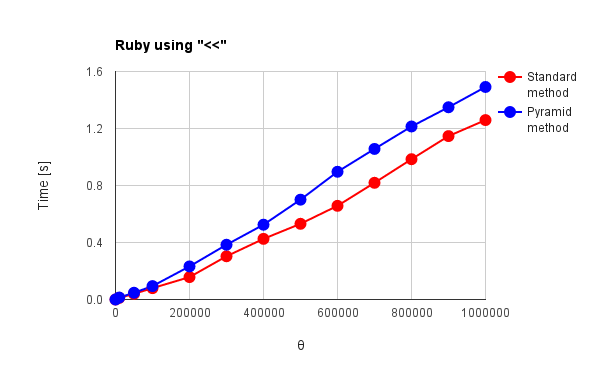
- "+"オペレータを使用して得た図2のNode.jsの結果と、"<<"オペレータを使用して得た図6(b)のRuby、"StringBuilder"を使用して得た図5(b)の結果は似た傾向がある。特に従来法の$\theta=1,000,000$でのNode.js, Rubyの処理時間は、それぞれ1.13秒、1.25秒と近い値になっている。
→ 最適化の手法が似ている可能性。
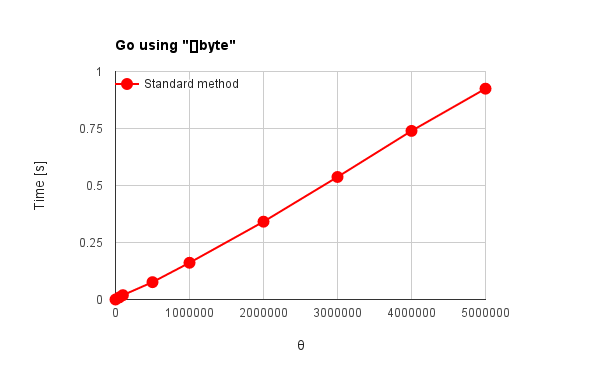
- "[]byte"メソッドを用いた図4(b), 図4(c)のGoの結果から、それぞれの処理時間に大きな差異が認められる。特に、図4(c)は図4(a)のピラミッド方式と同程度の結果になっている。
→ "[]byte"は従来法に特化した最適化が行われている。
上記の結果から最適化はピラミッド方式の効果を妨げることが分かりました。
ここでピラミッド方式の方が従来法よりも遅くなる現象について検討するため、総和処理中のループ数について考えます。
総和処理実行時のループ数$N_{l}$は、
N_{l} = \sum_{k=1}^{\omega - 1} \frac{\theta}{\phi^{k}} \tag{1}
のように表現できます。$\omega=0$のときは従来法で、$\omega \geqq 1$のときはピラミッド方式です。式(1)から$\omega$が大きくなると収束することが分かります。そのため、$\omega=0$のときの$N_{l0} = \theta$に対する$\omega=\infty$での$N_{li} = \theta(1 - \phi^{-1})^{-1}$の増加率$\varepsilon$は、
\varepsilon = 100 \times \frac{1}{(\phi - 1)} \tag{2}
になります。$\varepsilon$の単位は$%$です。使用可能な$\omega$は、$\omega=\log_{10} \theta - 1$になりますが、ループ数増加率が最大の$\omega$は1のときで、それ以上はマイナスのべき乗の等比数列になるため今回の測定で使用している$\phi=10$ではそれほど大きくはならず、定性的な検討には$\varepsilon$で問題ないと考えます。
さて、$\theta=1,000,000, \phi=10$のときの$\varepsilon$を計算すると11%になります。すなわち、この条件下での従来法から見たピラミッド方式でのループ数の増加は11%となり、これは100万要素に対して約11万程度のループ数増加を意味します。
図1 - 図6から総和処理が最適化されている言語では配列の要素を１つの文字列として加算するとき、加算場所である文字列のアドレスの最後尾に到達する速度が非常に速いのではないかと考えられます。このことと、上記のループ数の検討から、処理時間は総和処理スクリプト内で動く総データ量よりもむしろ1割程度増加するループ数に依存するようになり、結果としてピラミッド方式の方が従来法よりも処理時間が長くなるのではないかと考えています。g++では処理速度が速いため、これが顕著に現れているのではないかと考えられます。
様々な言語を同じ土俵の上（同じ計算機、同じアルゴリズム、同じ配列要素数）で複数の条件（従来法、ピラミッド方式、"+"オペレータ、加算専用メソッドあるいはオペレータ）を試すことができるということは、それらの結果を比較することでそれぞれの言語の特徴を知ることができると考えます。中でも最適化を可視化して比較ができる点は重要と考えます。
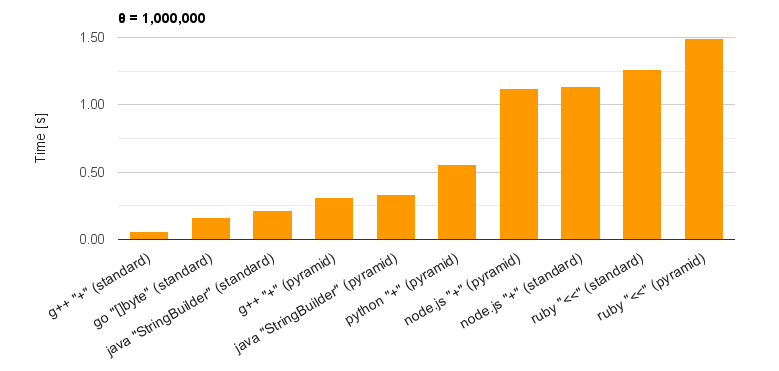
図 7: $\theta = 1,000,000$での各言語の処理時間トップ10.
図1 - 図6から$\theta=1,000,000$での各言語の処理時間をトップ10として並べてみました。（図7）ここで分かることは次の通りです。
-
実行時にコンパイルされる言語（g++, Go, Java）は処理速度が速い。
-
ピラミッド方式のPythonが従来法及びピラミッド方式でのNode.jsよりも速い。
→ ここだけを見ると、従来法では負けてしまいますが、ピラミッド方式ではPythonは、Node.jsのV8エンジンを上回ったと言えると思います。
-
Rubyの"<<"オペレータはNode.jsのV8エンジンに匹敵する能力がある。
-
ピラミッド方式ではPythonは、コンパイルされる言語とそうでない言語の中間に位置している。
→ ピラミッド方式の効果とも言える？
ピラミッド方式はGAS以外、今の場合Pythonでも効果が認められました。
結果
-
配列要素の総和処理について、ピラミッド方式はPythonに対しても効果があることが分かりました。さらにピラミッド方式のPythonは従来法、ピラミッド方式でのNode.jsよりも処理速度が速いことが分かりました。
-
"+"オペレータ、且つ、最適化されていない言語はピラミッド方式により効率化できることが分かりました。
-
言語に備わっている実行時の最適化はピラミッド方式の効果を低下させることが分かりました。これは、最適化が備わっている言語では配列要素の総和処理は従来法、且つ、専用のメソッドあるいはオペレータを使用して実行する方が好ましいことを意味します。
-
スクリプト実行時の最適化を可視化することができました。
もしも最適化の矛先を切り替える、あるいは最適化をオフにする手段があればピラミッド方式の恩恵を受けることができるかもしれません。実は、g++ではコンパイル時のオプションを'-O2'と'-O'で比較しましたが、全体の速度が変化するのみで$\theta$に対する処理時間の変化の振る舞いにはほとんど差は認められませんでした。他に最適化の切り替えのようなことは試したことがないためその手段がわかりません。これについては今後の課題ということで。
参考
Google Apps Scriptで配列要素の総和処理を高速で行いたい, 2016.10.14
付録
従来法
本記事で記載している従来法とは下記の疑似コードで示したアルゴリズムを指しています。
Declare a string variable arr, sum
Declare an integer variable loopcounter
Set arr to size n
for loopcounter = 0 to (size of arr) - 1
sum = sum + arr[loopcounter]
loopcounter = loopcounter + 1
endfor
実験で使用したスクリプト
測定で使用したスクリプトをこちらにまとめました。
最後に
-
改善点がありましたらご指摘下さいますと嬉しいです。
-
もしもすでにこのような内容をご存知の場合はお教え頂けますと幸いです。是非参考にさせていただきたいと思います。