この記事は九工大古川研 Advent Calendar 2020 15日目の記事です.
本記事は古川研究室の学生が学習の一環として書いたものです.
内容が曖昧であったり表現が多少異なったりする場合があります.
はじめに
研究室でよく使用・考察されている UKR (Unsupervised Kernel Regression) を
Pytorch という機械学習フレームワークを駆使して
ニューラルネットワーク風に組めないかという試みです.
UKR とは
UKR とは Unsupervised Kernel Regeression の略で,
その名の通り,教師なしのカーネル回帰アルゴリズムです.
観測されたデータに対して多様体でフィッティングし,
データの低次元表現を獲得します.
以下で軽く UKR の概要を説明します.
(物足りない感があるかもしれませんが,
本記事は UKR 自体の説明よりも
実装に重きを置いてますので悪しからず….)
問題設定
入力(観測変数)を $ \boldsymbol{X} = \{ \boldsymbol{x}_i \}_{i=1}^n, ,, \boldsymbol{x}_i \in \mathcal{X} $ として,
それを生成する元となった潜在空間中の変数(潜在変数) $\boldsymbol{Z} = \{ \boldsymbol{z}_i\}_{i=1}^n, ,, \boldsymbol{z}_i \in \mathcal{Z}$ と
潜在空間から観測空間への(滑らかな)写像 $f$ を
\forall i, \,\, \boldsymbol{x}_i \simeq f(\boldsymbol{z}_i),\,\, f: \mathcal{X} \rightarrow \mathcal{Z}
となるように推定します.
目的関数
$f$ と $\boldsymbol{Z}$ を具体的にどう推定するのかという話に移ります.
UKR のアルゴリズムでは,以下のように目的関数を定義します.
E(\boldsymbol{Z}) = \frac{1}{N} \sum_{i=1}^n \| \boldsymbol{x}_i - f(\boldsymbol{z}_i) \|^2 + \lambda \sum_{i=1}^n \| \boldsymbol{z}_i \|^2
ここで,写像 $f$ は以下の式で表現されるものとします.
f(\boldsymbol{z}) = \sum_i \frac{k(\boldsymbol{z}, \boldsymbol{z}_i) \boldsymbol{x}_i}{K(\boldsymbol{z})}
ただし,
\begin{align}
K(\boldsymbol{z}) &= \sum_{j} k(\boldsymbol{z}, \boldsymbol{z}_{j}) \\
k(\boldsymbol{z}, \boldsymbol{z^\prime}) &= \exp(- \frac{1}{2 \sigma^2} \| \boldsymbol{z} - \boldsymbol{z^\prime} \|^2)
\end{align}
この目的関数 $E$ を小さくするように学習します.
目的関数の第一項は「$i$ 番目の観測データの生成元となった潜在変数 $ \boldsymbol{z}_i $ を
写像 $f$ によって観測空間に写像した推定点 $ f( \boldsymbol{z}_i ) $ 」と
「実際に観測されたデータ $\boldsymbol{x}_i$ 」の二乗誤差です.
これをすべての $i$ について小さくすることで
$\forall i,,\boldsymbol{x}_i \simeq f(\boldsymbol{z}_i)$ となるように学習を進める働きを持ちます.
第二項は $\boldsymbol{z}_i$ の L2 ノルムで,学習を収束させる働きを持ちます.
$\lambda$ はその制約の強さを制御するハイパーパラメータです.
なぜこれが無いと収束しないのかと言いますと…(読み飛ばし可)
$f$ の定義より, $f(\boldsymbol{z}_i)$の値は$\boldsymbol{x}_i$だけでなく
$\boldsymbol{z}_i$近傍の潜在変数 $\boldsymbol{z}_j$ に対応する $\boldsymbol{x}_j$ の影響も受けます.
よって,目的関数の第一項$\left|\left|\boldsymbol{x}_i - f(\boldsymbol{z}_i)\right|\right|^2$を限りなく小さくするには,
$f(\boldsymbol{z}_i)$ が $\boldsymbol{x}_i$ 以外のデータから影響を一切受けない,
すなわち $\boldsymbol{z}_i$ が他の潜在変数から無限遠の場所にあればよいということになります.
つまり目的関数の第一項のみだと,潜在変数は永久に広がり続ける(= 収束しない)ということになります.
そのために,第二項によってある程度のところで収束させているというわけです.
また,仮に $\left|\left|\boldsymbol{x}_i - f(\boldsymbol{z}_i)\right|\right|^2 = 0$ となるまで学習をおこなったとして,
それは過学習に他ならなりません.
(目的関数について,ここでは直感的な説明をしていますが,
これは変分ベイズの観点からも理にかなっている目的関数です.
この辺りのお話は後日公開される
@ae14watanabe さんの記事で勉強させてもらいました.)
また,UKR においては($f$ の定義からもわかる通り),
写像 $f$ が潜在変数 $\boldsymbol{Z}$ によって一意に決まるため
実質的には $\boldsymbol{Z}$ の推定のみを行うことになります.
$\boldsymbol{Z}$ は勾配法で推定します.
実装
…の一部を以下で紹介します.
実装の全貌は Gist で公開しています.
UKR-Layer
PyTorch で言うカスタムレイヤーで UKR を実装します.
このレイヤーの入力は観測データ $\boldsymbol{X}$ で,
出力は $\boldsymbol{X}$ の推定点 $\boldsymbol{Y} = \{ f(\boldsymbol{z}_i) \}_{i=1}^n$ です.
内部に潜在変数 $ \boldsymbol{Z}$ をパラメータとして保持します.
class UKRLayer(nn.Module):
def __init__(self, data_num, latent_dim, sigma=1, random_seed=0):
super().__init__()
self.kernel = lambda Z1, Z2: torch.exp(-torch.cdist(Z1, Z2)**2 /
(2 * sigma**2))
torch.manual_seed(random_seed)
self.Z = nn.Parameter(torch.randn(data_num, latent_dim) / 10.)
def forward(self, X):
kernels = self.kernel(self.Z, self.Z)
R = kernels / torch.sum(kernels, axis=1, keepdims=True)
Y = R @ X
return Y
UKR-Net
UKR-Layer をただ一つ持つニューラルネットワークを構築します.
これの説明に関しては公式のチュートリアル にもあるような話ですので割愛します.
class UKRNet(nn.Module):
def __init__(self, N, latent_dim=2, sigma=2):
super(UKRNet, self).__init__()
self.layer = UKRLayer(N, latent_dim, sigma)
def forward(self, x):
return self.layer(x)
データセットの用意
主題とちょっと逸れるので読み飛ばしてもらっても大丈夫です.
双曲放物面状のデータ分布を生成する
gen_saddle_shape 関数を生成します.
式で書き表すと以下のようになります.
f(\boldsymbol{z}_1, \boldsymbol{z}_2) = \begin{pmatrix}
\boldsymbol{z}_1 \\
\boldsymbol{z}_2 \\
\boldsymbol{z}_1^2 - \boldsymbol{z}_2^2
\end{pmatrix}
学習スクリプト
そして学習時に回すスクリプトです.
これもいわゆる PyTorch の基本形以上のことはしていません.
変わっていることといえば
学習と描画を分けるために結果を pickle で保存していることくらいです.
また,目的関数の $\lambda$ (潜在変数のスケールに対する制約の強さ)は
optimizer の weight_decay で設定しています.
# プロセッサの設定
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
# データの準備
X = torch.from_numpy(gen_saddle_shape(N := 100).astype(np.float32)).to(device)
X_train = X.repeat(samples := 1000, 1, 1)
train = torch.utils.data.TensorDataset(X_train, X_train)
trainloader = torch.utils.data.DataLoader(train, batch_size=1, shuffle=True)
# モデル,学習の設定
model = UKRNet(N).to(device)
criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(),
lr=0.01,
momentum=0.9,
weight_decay=1e-4)
# 学習結果,loss 保存用の変数
num_epoch = 200
Z_history = np.zeros((num_epoch, N, 2))
losses = []
# 学習ループ
with tqdm(range(num_epoch)) as pbar:
for epoch in pbar:
running_loss = 0.0
for i, data in enumerate(trainloader):
inputs, targets = data
inputs, targets = Variable(inputs), Variable(targets)
optimizer.zero_grad()
outputs = model(inputs)
loss = criterion(outputs, targets)
loss.backward()
optimizer.step()
running_loss += loss.item()
# 潜在変数の保存
Z_history[epoch] = model.layer.Z.detach().cpu().numpy()
# loss の値の保存
losses.append(running_loss)
# プログレスバーの表示
pbar.set_postfix(
OrderedDict(epoch=f"{epoch + 1}", loss=f"{running_loss:.3f}"))
# Loss の推移の描画
plt.plot(np.arange(num_epoch), np.array(losses))
plt.xlabel("epoch")
plt.show()
# 学習結果を *.pickle で保存
with open("./X.pickle", 'wb') as f:
pickle.dump(X.detach().cpu().numpy(), f)
with open("./Z_history.pickle", 'wb') as f:
pickle.dump(Z_history, f)
結果
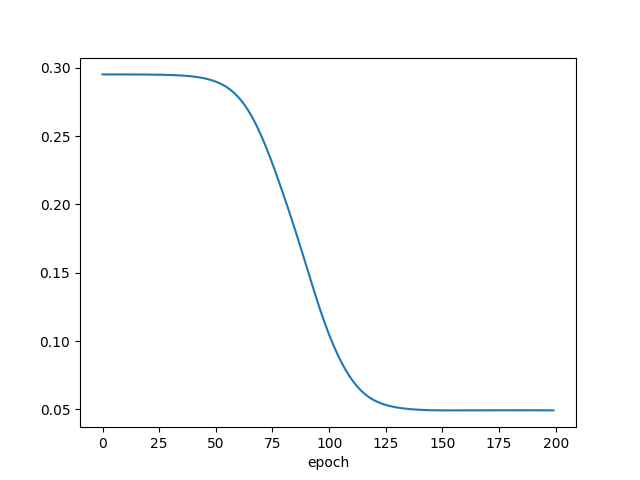
epoch ごとの目的関数の値の推移をプロットしました.
いい感じに学習できてそうですね.
次に,実際にデータに対して多様体でフィッティングできているかを
描画して確認します.
多様体推定もできていますね.
ちょっといつもの学習結果と違う感じもしますが,
これは勾配法のアルゴリズムに
Stochastic Gradient Descent (SGD)を使っているからと思われます.
所感
PyTorch の力を借りているので
numpy でフルスクラッチ実装するときと比べて
- 目的関数や勾配法のアルゴリズムを変えるなどのアレンジがしやすい
- GPU の力を容易に借りられる
などの点が良いなと思いました.
おわりに
本当は多層化してみた〜みたいなことがしたかったのですが,
アドカレに間に合わせるには時間が足りなかったです.
これが何かに応用できる日が来たら良いなあと思っています.
とりあえず勾配法のアルゴリズムをいろいろ変えて遊んでみるとします.