はじめに
素人同然である私が知識を付けるための記事です。間違いも多くあると思いますが、そこは生暖かい目で見て頂ければ幸いです。アドバイスやご指摘などございましたら助かります。
背景
前回、AutoEncoderがある程度の実感を持って理解できた気がします。AutoEncoderを書く際、VAE(Variational AutoEncoder:変分オートエンコーダー)の記述を見ました。VAEでは正規分布からサンプリングした潜在変数Zを元にデータを再構築すると知りました。確率分布からデータを生成する事は以前から知りたい事で、GANの様に確率分布を想定しないで経験から確率分布を作ってデータを生成する事は是非とも理解して応用したい所です。
前回の記事
AutoEncoderを理解する。(2020.4.12)
目的:VAEを通して生成モデルを理解したい。
確かに、AutoEncoderも生成モデルなのですが、統計との関係を明確にしたいです。VAEではサンプルから確率分布(正規分布)を推定し、その確率分布からサンプリングした物をデコードする事でデータを再構築します。特に、サンプルから確率分布を推定するとはどういうことかを中心に理解したいです。
AutoEncoderとの違い
簡単に言うと、潜在変数Zについて確率分布を考えるかどうかだと思います。正規分布を考えるらしいのですが、Encoderで平均ベクトル$\mu$と分散ベクトル$\sigma$を算出します。
詳しくはG検定のテキスト(参考2など)をご参照下さい。
実装:Yunjey Choi(2020.4)、pytorch-tutorial
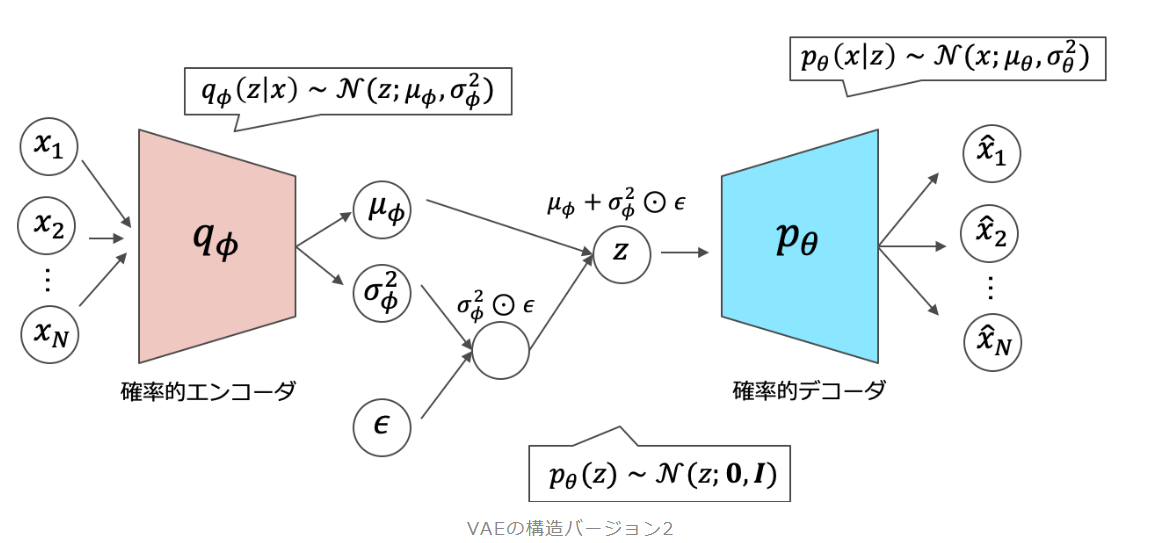
モデルの構造
大まかなモデルの構造は上の通りです。大きく、エンコーダー、潜在変数、デコーダーに分類すると分かり易いと考えています。次にそれぞれの役割を見ていきます。
- エンコーダー
入力を圧縮します。今回は784次元を20次元に圧縮します。圧縮された20次元のデータはそれぞれ、平均ベクトルmuと分散ベクトルの対数log_varとして処理されます。 - 潜在変数Z
実装的には、エンコーダーで求めた平均ベクトルmuと分散ベクトルの対数log_varを用いて潜在変数を算出します。理論的には正規分布$N(mu,$ log_var$)$よりサンプリングされます。 - デコーダー
潜在変数Zを復元して、文字を生成します。今回は20次元の潜在変数Zを784次元の文字を表すデータに復元します。
つまり、1文字ずつ正規分布を推定する事になってそうです。
ソースコード
1.Encoderのアウトプット
ここでは平均ベクトル$\mu$と分散ベクトル$\sigma$をどのように算出しているのかを見ていきます。コードは
x_reconst, mu, log_var = model(x)
に関して詳細に見ていきます。ここでのアウトプットmu、log_varがそれぞれ「平均ベクトル」と「分散ベクトルの対数」をとったものです。なぜ対数を取るかはその方が計算しやすいとしか理解していません。詳細は参考にある資料をご覧ください。
まずは、VAEのモデルのコードを確認します。ここで確認したいのは平均ベクトルと分散ベクトルが求められるまです。
class VAE(nn.Module):
def __init__(self, image_size=784, h_dim=400, z_dim=20):
super(VAE, self).__init__()
self.fc1 = nn.Linear(image_size, h_dim)
self.fc2 = nn.Linear(h_dim, z_dim)
self.fc3 = nn.Linear(h_dim, z_dim)
self.fc4 = nn.Linear(z_dim, h_dim)
self.fc5 = nn.Linear(h_dim, image_size)
def encode(self, x):
h = F.relu(self.fc1(x))
return self.fc2(h), self.fc3(h)
def forward(self, x):
mu, log_var = self.encode(x)
z = self.reparameterize(mu, log_var)
x_reconst = self.decode(z)
return x_reconst, mu, log_var
これはモデルだけですので、実行するコードも見てみます。
for epoch in range(num_epochs):
for i, (x, _) in enumerate(data_loader):
# Forward pass
x = x.to(device).view(-1, image_size)
x_reconst, mu, log_var = model(x)
恐らく、modelのforwardメソッドで平均ベクトルmuと分散ベクトルlog_varを出していそうです。その部分を再掲します。
mu, log_var = self.encode(x)
出力を見ると、mu, log_var共に20次元のデータが128個ずつあります。これらから正規分布$N(\mu,\sigma)$を推定しているのは間違いないのですが、今は理解を優先したいので割愛します。
実行部を見ると、model(x)で再構築したデータも出力しています。それがx_reconstだと思います。そのコードを再掲します。
x_reconst, mu, log_var = model(x)
このx_reconstを可視化すると次のようになりました。
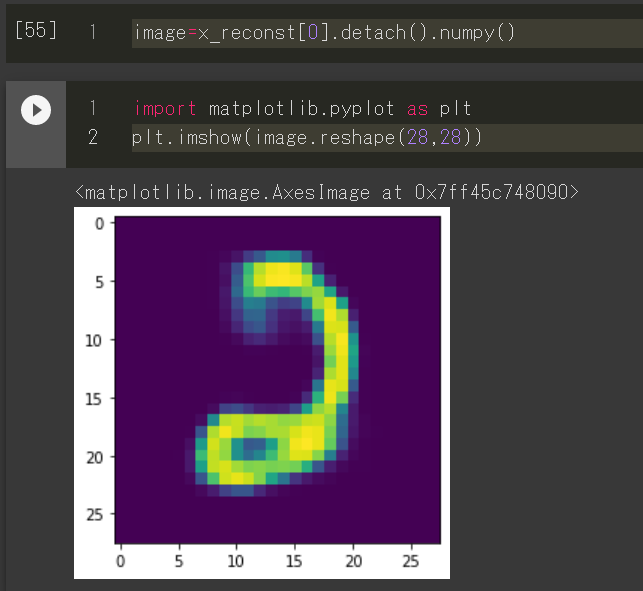
数字っぽい物が出来ている様です。
2.サンプリング
次に見るのは、推定した確率分布から潜在変数Zをサンプリングする所です。これもVAEクラスのforwardメソッドに入っているので、該当部分だけを再掲します。
z = self.reparameterize(mu, log_var)
このreparameterize関数はVAE特有の物です。Reparamatrization Trickというみたいで、誤差逆伝搬するための工夫との事です。詳細は「参考1.我妻」をご覧下さい。
このあと、デコードして先程の数字っぽい物を生成します。
サンプルの入力から潜在変数Zを求め、数字っぽい物を再構築するまでの一連の流れはVAEクラスに記述されていますので再掲します。
def forward(self, x):
mu, log_var = self.encode(x)
z = self.reparameterize(mu, log_var)
x_reconst = self.decode(z)
return x_reconst, mu, log_var
reparameterizeメソッドの説明は割愛しますが、平均ベクトルmuと分散ベクトルlog_varを使って潜在変数zを算出しているのが分かります。これがサンプリングのコードです。
感想
ここでの目的が「VAEを通して生成モデルを理解したい。」という事でした。簡単には
- サンプルを入力する
- 平均ベクトルと分散ベクトルを算出する
- 正規分布から潜在変数Zをサンプリングする
- 潜在変数Zより数字を生成する
の手順をコードを元に追っていけました。Reparametrization Trickより、近似的に正規分布からサンプリングする事も感覚的に理解できた気がしています。勘違いでも分かった気になる事が次に繋がると考えています。
課題
- 次はGANを見ていきたいです。また、StreamlitにGANで人物を生成するアプリのチュートリアルもあった気がしたので、次はアプリの実装と共に理解を深めたいです。
- サンプルを128個のバッチで分けていますが、平均ベクトルと分散ベクトルも128個ずつ算出されています。それが正規分布を128個ずつ作っているのか、128個の平均を取っているのか分かっていません。その辺も理解を深めていきたいと思います。=>コードを見直すと、
参考
- 我妻幸長(2020.4)、【3-2: VAEの仕組み】AIによる画像生成を学ぼう! 【VAE、GAN】、YouTube
- 猪狩宇司(2021.4.27)、深層学習教科書 ディープラーニング G検定(ジェネラリスト)公式テキスト 第2版、翔泳社
- Yunjey Choi(2020.4)、variational_autoencoder.main.py、GitHub
- aidiary(2020.4)、人工知能に関する断創録、PyTorch (11) Variational Autoencoder、HatenaBlog