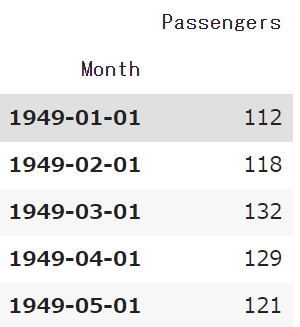背景
統計検定2級の範囲である統計的推定・検定、一元配置分散分析を終えたので準1級の学習を始めました。私の学習の手順として自分が学びたい所から始めるというのがあります。今回は前から適当な理解しか出来てなかったので、これを機にきちんと学びたいと思いました。
データの読み込み
今回は「航空会社の国際線での乗客数」のデータを使います。いつもの様にpandasで読み込みます。
# データセットの読み込み
import pandas as pd
url='https://www.salesanalytics.co.jp/591h' #データセットのあるURL
df=pd.read_csv(url, #読み込むデータのURL
index_col='Month', #変数「Month」をインデックスに設定
parse_dates=True) #インデックスを日付型に設定
df.head() #確認
成分分解
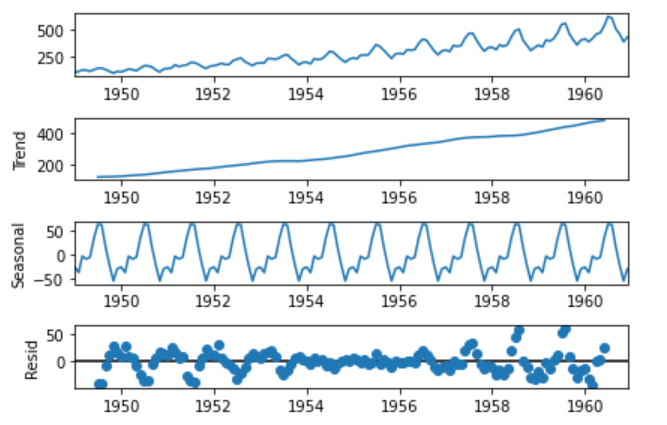
まずは、データを可視化します。元のデータを原系列と言うそうです。トレンドと季節性変動、ノイズも自動で表示出来ます。
res = sm.tsa.seasonal_decompose(df)
fig = res.plot()
自己相関
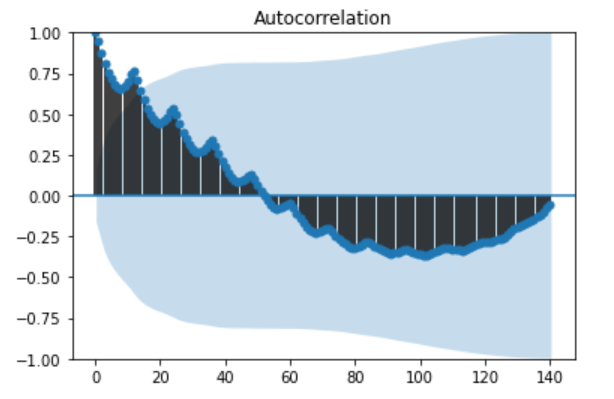
自己相関を140個先のデータまで見ていきます。一番最初のデータをt=0として、始めはt=0同士を比べて自己相関は1となります。次はt=1と比べる、その月はt=1と、、、という感じでt=140まで見ていきます。
acf=sm.graphics.tsa.plot_acf(df, lags=140)
偏自己相関
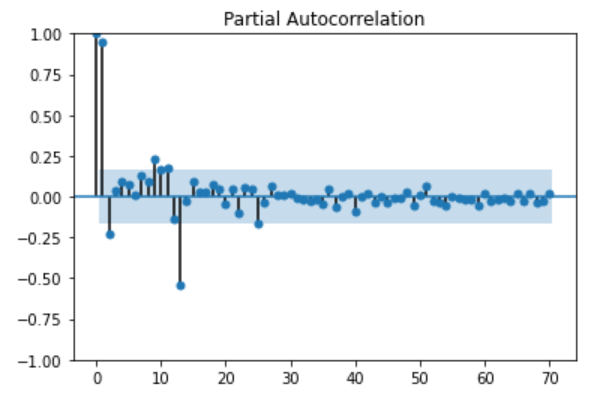
自己相関がt=0の時とt=0,t=1,t=2と見比べていくのに対し、偏自己相関ではt=0とt=0、t=0とt=n(任意の自然数)、t=0とt=2n、、、のように任意のn個先を見ていくという認識です。ただ、この認識ではPythonで図示したものとずれがありました。そもそもPythonでの書き方も分かっていないのですが、もしお分かりの方がいらっしゃいましたら教えて頂けると助かります。ご意見やアドバイス等ありましたら是非ともよろしくお願いします。
pacf=sm.tsa.graphics.plot_pacf(df, method='ywm', lags=70)
ADF検定(弱定常性の確認)
拡張ディッキーフラー検定という、弱定常性を求める手法の様です。これは小さいほど良いそうです。これを原系列から順にみていきます。
#原系列
df.plot()
sm.tsa.adfuller(df['Passengers'])[1]
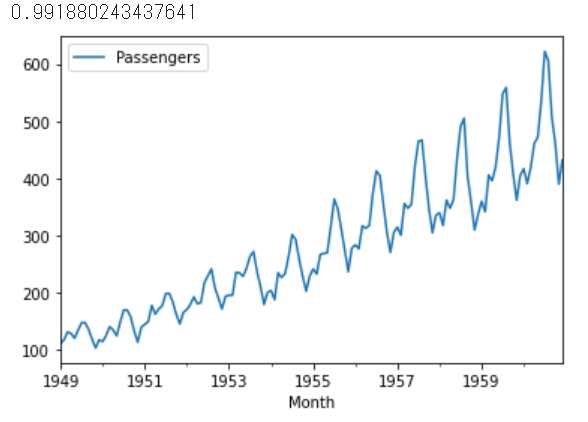
原系列は0.99...となりました。
次に差分を見ていきます。
#原系列の差分を取ることでトレンドの分散が残っている気がする
df.diff().plot()
sm.tsa.adfuller(df.diff().dropna()['Passengers'])[1]
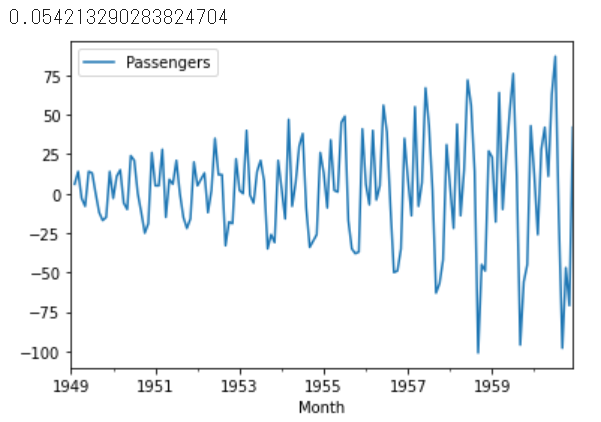
0.054...となりました。波形を見ると、0を中心に振幅が大きくなっている様に見えます。これは1月前の値との差が年を経る毎に大きくなっていると考えています。つまり、トレンドは消えているのに、トレンドの分散は残っているというイメージです。
次に対数化したものを見ていきます。
#対数化(トレンドの分散が取り除かれてる気がする。要するにtrendとseasonalが残る)
ldf=np.log(df)
ldf.plot()
sm.tsa.adfuller(ldf['Passengers'])[1]
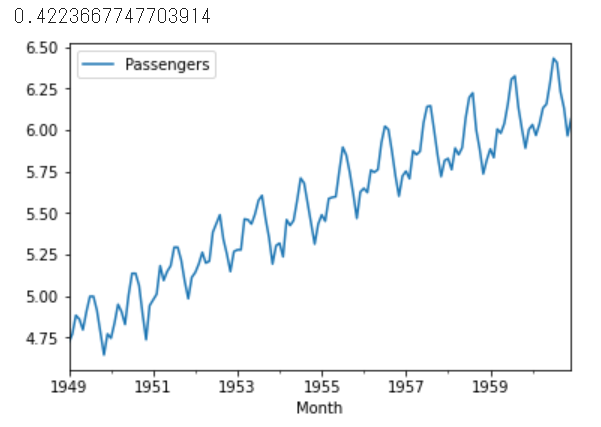
原系列に比べるとシンプルになりました。同じ大きさの波が一定の上昇を見せながら上がっていっています。原系列では時を経る毎に波が大きくなっていましたが、対数を取るとそれが無くなっている様に見えます。ADFは0.42,,,となりました。差分を取った時より定常性はなくなっている様です。
次に、対数を取った物の差分を見ていきます。また、ここでは差分と階差を同じものとして使っていますが、詳細は分かっていません。ご意見・アドバイスなど大歓迎です。非難・批判はやさしめにして頂けると幸いです。
#対数化+階差
ldf.diff().plot()
sm.tsa.adfuller(ldf['Passengers'].diff().dropna())[1]
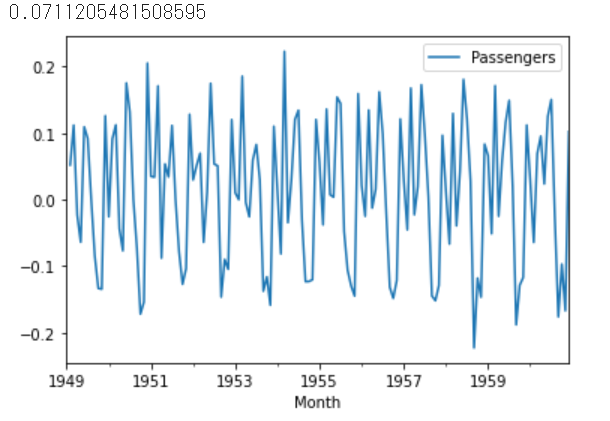
原系列の差分を取った時は、波の形が徐々に大きくなっていましたが、対数化した物の差分を取ると、波の大きさは一定に近い様です。ただ、0.071,,,と定常性からは離れています。
次に、対数化した物から季節性を除いた物を見ます。
#対数化+季節性の除去
#トレンドとノイズが残っている気がする
res=sm.tsa.seasonal_decompose(ldf)
seasonal_adjust=(ldf.Passengers-res.seasonal)#ldf.Passengers
seasonal_adjust.plot(legend=False)
sm.tsa.adfuller(seasonal_adjust)[1]
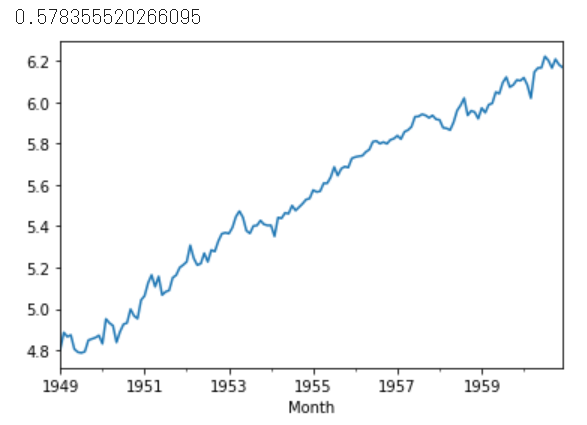
対数化した物を図示すると、同じ大きさの波が昇っていくような感じでしたが、季節性を取り除くと、波がほぼなくなり、y=xの様に(は言い過ぎですが)なりました。ADFは0.57,,,となりました。トレンドが入ると定常性は失われるようです。
最後に、先ほどの波形の差分を取った物を見ます。
#対数化+季節の除去+差分(トレンドの除去)
res=sm.tsa.seasonal_decompose(ldf)#対数化
seasonal_adjust=(ldf.Passengers-res.seasonal)#ldf.Passengers#季節性の除去
seasonal_adjust.diff().plot(legend=False)#差分
sm.tsa.adfuller(seasonal_adjust.diff().dropna())[1]
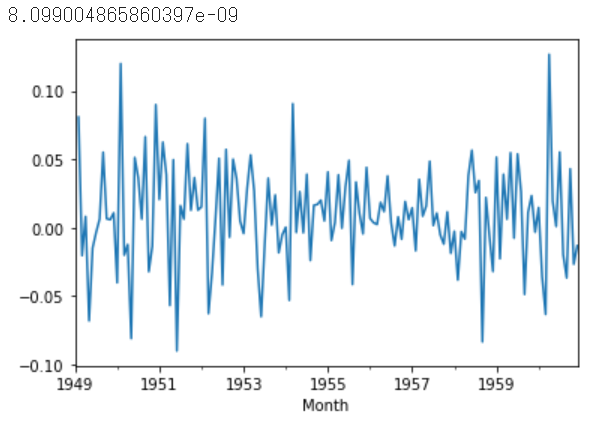
トレンドもなくなり、0を中心とした不安定そう波が出来ました。ただ、ADFの値は$8.09\times10^{-9}$となり、定常と言えそうな気がします。
統計モデルの作成
定常性を確認できたので、いよいよ統計モデルの作成に進みます。ここではSARIMAXを使っていますが、説明変数を設定していないのでSARIMAモデルと同意のはずです。引数のパラメータはメソッドを使って決めています。これは後日追記するか、新しい記事を作るかもしれません。
mod_seasonal = sm.tsa.SARIMAX(ldf, trend='c', order=(1,1,1),
seasonal_order=(0,1,2,12))#order=(AR,MR,R) seasonal_order=S
res_seasonal = mod_seasonal.fit()
res_seasonal.summary()
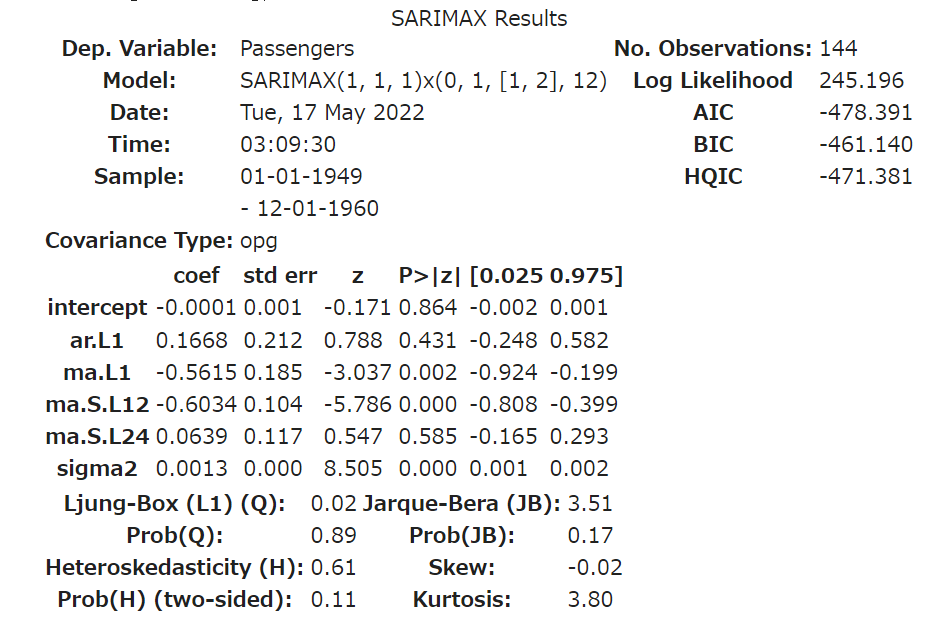
結果についていろいろ解説したい所ですが、理解が追い付いておらず出来ません。申し訳ありませんが、後日、追記もしくは新しい記事のリンクを貼らせて頂きたいと思います。
推定と統計的推測
いよいよ予測になります。モデルを作って予測する辺りは機械学習と同じですね。今回は1961年1月から36ヶ月の予測をしています。36ヶ月はモデル名.forecast(36)の様に期間を指定するだけの様です。モデルの中に自分が保有しているデータの日時は入っている様に思えます。上で定常性を確認する時、差分や対数化、季節性の除去などを行いましたが、モデルの内部でも同じような事が行われ、forecastで原系列の状態に戻しているのかと考えています。と言った所で気付きましたが、今回は対数化については自分でやっているようです。最後の図についても結果は対数化した状態になっていますね。
pred = res_seasonal.forecast(36)
ax = ldf.plot()
pred.plot(ax=ax)
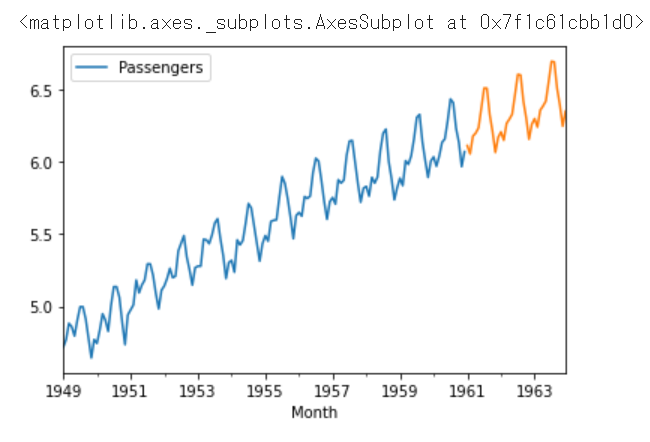
青が元のデータ、オレンジが予測です。それっぽい予測が出来ている様に思えます。これはそれっぽいじゃなくて、理論的にこうなっているんでしょうが、それを説明できる程に理解できていません。こちらについても追記もしくは新しい記事のリンクを貼らせて頂きたいと思います。
感想
今回は時系列解析について実装をメインに書かせて頂きました。今まで適当に実装・予測はしていたのですが、統計検定の学習を兼ねて理論を学ばせてもらおうと思いました。ただ、これが予想以上に難航し、状態空間モデルの理解に行く前に、一旦、投稿させて頂いております。中途半端な投稿になっておりますので、理解の間違えや入れるべき項目が無かったりと不備が目立つと思います。ご意見・アドバイスなどありましたら助かります。非難・批判はやさしめにお願いします。