背景
前回、谷合棋士の本を参考に統計的仮説検定を行いました。今回は、たまたま見つけたts0818さんのブログ(ts0818(2020.4)、Pythonでt検定するには、Scipyを使うのが便利らしい)を参考に記事にさせてもらっています。
前回の記事
統計的仮説検定(2020.4.22)
目的
統計的仮説検定に慣れる事とPythonで解ける様になることを目的にしています。
問題
解答
どういう問題か(問題の分類)
今回は、母平均の検定です。確率分布としてはt分布を想定します。標本分布とt分布を比べる様なイメージをしています。求めたいのは母平均$\mu$が50.2かどうかです。
どのように解けるか(Python)
まずはライブラリをインポートします
import numpy as np
import scipy as sp
import scipy.stats as stats
from matplotlib import pyplot as plt
データを読み込みます。
height = np.array([
51.0, 45.9, 48.8, 54.0, 53.5,
48.0, 44.5, 46.0, 50.3, 48.0
])
標本から検定統計量を算出します。これはt値を求める際、必要になります。
# 検定統計量
n = len(height) # サンプル数
k = n -1 # 自由度
u_var = np.var(height, ddof=1) # 不偏分散
statistical_sample_mean = np.mean(height) # 標本平均
さきほど求めた検定統計量からt値とp値を算出します。
# 仮説
statistical_population_mean = 50.2 # 母平均
t, p = stats.ttest_1samp(height, popmean=statistical_population_mean)
print(f"母平均が{statistical_population_mean}のt値:{t}")
print(f"母平均が{statistical_population_mean}である確率(p値):{p}")
t値は-1.19、p値は0.27、
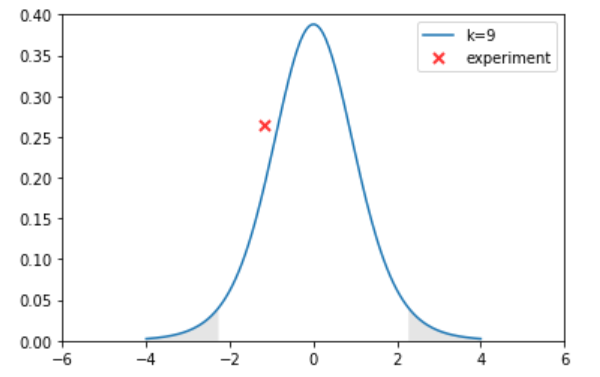
自由度9のt分布の両側5%点(棄却域)は2.26$\leq |t|$だから、帰無仮説を有意水準5%で棄却できません。最後に、図示します。
# グラフ描画
x = np.linspace(-4, 4, 200)
flg, ax = plt.subplots(1, 1)
# t分布を描画
ax.plot(x, stats.t.pdf(x, k), linestyle="-", label="k="+str(k))
# t分布に今回の確率分布を表示させる
ax.plot(t, p, "x", color="red", markersize=7, markeredgewidth=2, alpha=0.8, label="experiment")
# t分布の95%信頼区間から外れた領域を描画する
bottom, up = stats.t.interval(alpha=0.95, loc=0, scale=1, df=9)
plt.fill_between(x, stats.t.pdf(x, k), 0, where=(x>=up)|(x<=bottom), facecolor="black", alpha=0.1)
plt.xlim(-6, 6)
plt.ylim(0, 0.4)
plt.legend()
plt.show()
どのように解けるか(解法)
有意水準5%が基準になります。今回は両側検定なので、棄却域が半分ずつに分かれます。これはt分布表に従い、臨界値はPythonではscipy.stats.t.interval(0.95, df)で求められます。今回は自由度dfが9です。臨界値は上側と下側が出ますが、それぞれ-2.26,2.26になります。
次にt値を求めます。stats.ttest_1samp(height,popmean)でt値とp値がそれぞれ算出されます。今回は-1.18でした。
さきほどの臨界値とt値を比べて、結論を出します。-2.26<t(-1.18)なので棄却できません。
参考
感想
今回は1標本の平均の検定を行いました。今回は標本分布とt分布を比べているという認識です。仮説検定には母平均を使っています。まだまだ慣れないためか記事に書こうとすると全く進みません。今は質より量で雑な記事を量産して後で修正出来ればと思います。