背景
前回は2標本の平均の差の検定、筋トレ前後のテストの差の確率分布を作って、それが正規分布かどうかを検定値を用いて判断するのでした。これは母分散がわからない場合の正規分布の母平均の検定、すなわち1標本のt検定と同意です。今回は対応のないt検定に取り組みたいと思います。今回は統計WEBから問題をピックさせて頂きたいと思います。
前回の記事
統計的推定と検定をPythonで解く「統計的仮説検定(2標本の平均の差の検定、対応のあるt検定」(2020.4.25)」
問題
ある学校の1組と2組の算数のテストの平均点を比較します。1組の生徒30人の平均点は75点、標準偏差は5点、2組の生徒32人の平均点は70点、標準偏差は8点でした。この結果から、1組と2組の算数のテストの平均点に差はあると言えるでしょうか。
解答
どういう問題か(問題の分類)
対応の無い2標本の平均値の差の検定です。これは2つの対応のない標本(別々の母集団から抽出したと考えられる標本)が本当に別々の母集団から抽出されたかどうかを知りたいです。これを知るには2つの標本分布の差が正規分布に従うかどうかを見れば良さそうです。
どのように解けるか(概要)
2つの標本に差があるかどうかは、2つの標本の平均点を比較すれば良さそうです。そのため、$\mu_{1}$を1組のテストの平均点、$\mu_{2}$を2組のテストの平均点として、次のような仮説検定を行う事を考えます。
*帰無仮説:$\mu_{1}$-$\mu_{2}=0$
*対立仮説:$\mu_{1}$-$\mu_{2}≠0$
どのように解けるか(Python)
今回はデータが無く代表値だけです。ですが、それではPythonの練習になりませんので、1組のデータがx1に、2組のデータがx2に入っているとします。 それっぽいデータを生成します。この方法は@WolfMoonさんに教えてもらいました。いつもありがとうございます。
まずは、平均と標準偏差を確認します。これは問題文にあるので、そのまま変数に入れます。
n1, mean1, std1 = 30, 75, 5
n2, mean2, std2 = 32, 70, 8
次に、以下の順番で上記の「データ数、平均、標準偏差」に従ったデータを生成できます。
- まずは何でも良いので乱数でデータを生成します。
- 次にこのデータが平均値0、標準偏差1になるように標準化します。
- 標準化したデータを、始めに確認した平均値$mean_x$と標準偏差$std_x$($x$は1か2)になるように線形変換します。
- 最後に、偏差値と標準偏差を確かめます。
これをまとめてプログラムにします。
x1 = np.random.randn(n1)
x1 = (x1 - np.mean(x1)) / np.std(x1, ddof=1)
x1 = x1 * std1 + mean1
len(x1), np.mean(x1), np.std(x1, ddof=1)
これを1組のデータとします。2組のデータはx1をx2に入れ替えて作ります。
このデータを使ってt値を算出します。2標本のt検定はscipy.statsのttest_ind関数で計算出来ます。equal_value=Trueにすることでウェルチの方法を使わずに計算します。
t, p = st.ttest_ind(x1, x2, equal_var=True)
今回はデータが無いので計算できませんが、下で計算する様に t値は約2.93となり、p値は棄却域に入ると想定されます。これより、「有意水準5%の両側検定において、帰無仮説は棄却され、対立仮説が採択される」という結果になります。つまり、「1組と2組の算数のテストの平均点には差がある」と結論づけられます。
どのように解けるか(解法)
2つの標本に差があるかどうかを統計的に知りたいです。2つの標本に差があったら、1組と2組でテストの点数が違うはずです。つまり、1組と2組のテストの点数の確率分布が異なる事を統計的に求めたいです。これは1組と2組のテストの点数の差がない、つまり、$\mu_1-\mu_2=0$を棄却することで求めます。
この時、自由度60に従うt分布の有意水準5%で帰無仮説が棄却されます。1組と2組の算数のテストの平均点に差があるかどうかを調べることが目的なので、両側検定を行います。統計数値表から$t_{0.025}(60)$の値を読み取ると「2.000」となっています。次にt値を求めます。
$$
t=\frac{\bar{x}_1-\bar{x}_2}{\sqrt{s^2(\frac{1}{n_1}+\frac{1}{n_2})}}=\frac{\bar{x}_1-\bar{x}_2}{s\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}
$$
今回の標本では2つの標本の不偏分散を用いて算出した「プールした分散$s^2$」を使います。「プールした分散$s^2$」は次の様に求められます。
$$
s^2=\frac{(n_1-1)\times s_1^2+(n_2-1)\times s_2^2}{n_1+n_2-2}=45.15
$$
これより
$$
t\fallingdotseq2.93
$$
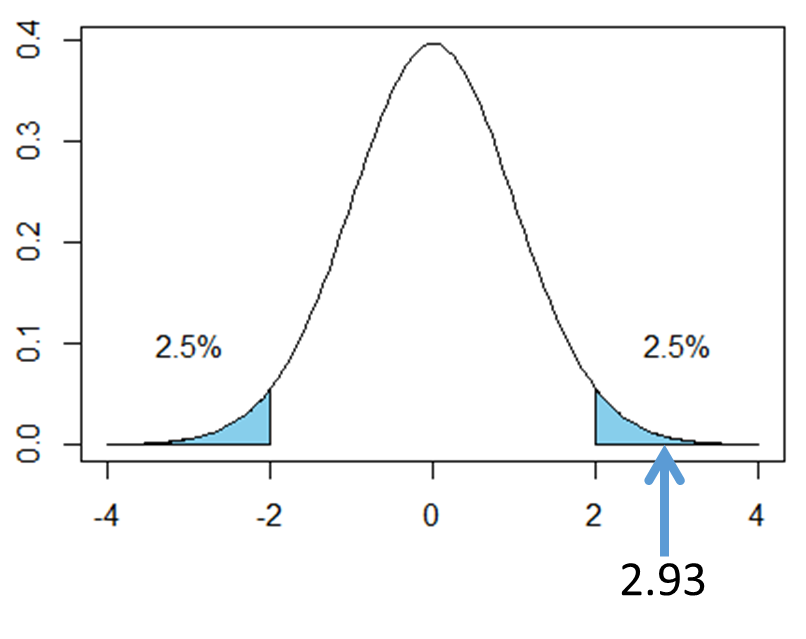
次の図は自由度60のt分布を表したものです。t=2.93は図の矢印の部分に該当します。矢印は棄却域に入っていることから、「有意水準5%の両側検定において、帰無仮説は棄却され、対立仮説が採択される」という結果になります。つまり、「1組と2組の算数のテストの平均点には差がある」と結論づけられます。
参考
感想
先日、対応のあるt検定が分かったつもりなり、勢い余って対応のないt検定をしました。ここで、ウェルチの方法とそうでない方法がある事を知り、まずは基本っぽいウェルチの方法を使わない方を行いました。2標本の検定統計量は初めて出てきたと思います。また、プールした分散$s^2$という言葉も計算方法も初めて知りました。これで2標本についての検定が出来るのがまだ不思議ですが、そのうち理解できればと思います。
#次の記事
統計的推定と検定をPythonで解く「統計的仮説検定(2標本の平均の差の検定、対応のないt検定、ウェルチの方法)」(2020.4.28)