背景
「ウェルチの方法を使った対応のない2標本の平均の差のt検定」をしたので、次は「単回帰分析」かと思っていました。いろんな資料を見ていくと「分散分析」があったり、統計検定2級に沿っていくと「一元配置分散分析」があったりで、いつの間にか「単回帰分析」と「一元配置分散分析」をごっちゃにして考えていました。とりあえず、一番シンプルっぽい「一元配置分散分析」を解いて次に進みたいと思います。いろんな物を見ていく内に「対応のあるない」の記述がありましたが、前回までの私の認識としては母集団が同じかです。それにより、差の分布で判断するか、それぞれの分布の差で判断するのかの違いがあると思っています。
今回は「とけたろう(2022.5)、一元配置分散分析【中学の数学からはじめる統計検定2級講座第16回】、Youtube」を使わせて頂いています。
前回の記事
統計的推定と検定をPythonで解く「統計的仮説検定(2標本の平均の差の検定、対応のないt検定、ウェルチの方法)」(2020.4.28)
目的:分散分析表を作れる
まずは、分散分析表を作れる事を目指します。
問題
解答
どういう問題か(問題の分類)
どのように解けるか(概要)
*帰無仮説:$\mu_{1}=\mu_{2}=\mu_{3}$
*対立仮説:少なくとも一つの群の平均が異なる
どのように解けるか(Python)
今回は、分散分析表を一つ一つ出していきます。最後のF値を出す時はscipyのstats.f_oneway関数を使いますが、それ以外はプログラミングの恩恵を受けている感じがしません。もし、ご存じの方がいらっしゃったらコメントで教えて頂けると嬉しいです。
まずはライブラリのインポートです。
from scipy import stats
import pandas as pd
import numpy as np
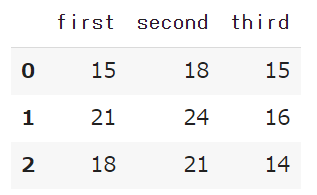
データを読み込みます。問題に沿って手打ちです。
first = np.array([15, 21, 18])
second = np.array([18, 24, 21])
third = np.array([15, 16, 14])
data = pd.DataFrame({'first':first, 'second':second,'third':third})
a=data.shape[1] #水準間の自由度
n=data.shape[0]*data.shape[1] #全データ数
data
水準内平均、全体の平均、水準間平方和、残差平方和をそれぞれ算出します。ここがプログラミングの恩恵に預かれないポイントです。今後、新しい情報が入りましたら追記します。
#水準内平均
level_means=data.mean()
level_means
#全体の平均
all_mean=data.mean().mean()
all_mean
#水準間平方和
Sa = 0
for name in data.columns:
Sa += data[name].shape[0]*((level_means[name]-all_mean)**2)
Sa
#残差平方和
Ra = 0
for name in data.columns:
for i in range(a):
#print((data[name]-level_means[n])**2)
Ra += ((data[name][i]-level_means[name])**2)
Ra
最後にF値とp値を求めます。ここだけはscipyのstats.f_oneway関数を使わせてもらいます。
#F値、P値
f, p = stats.f_oneway(first,second,third)
print(f"F={f:.2f}, p-value = {p:.2f}")
最後に分散分析表を作ります。
#分散分析表の作成
ANOVA=pd.DataFrame(columns=['平方和', '自由度', '平均平方和'], index=['水準間','残差'])
ANOVA.loc['水準間']['平方和']=Sa
ANOVA.loc['残差']['平方和']=Ra
ANOVA.loc['水準間']['自由度']=a-1
ANOVA.loc['残差']['自由度']=n-a
ANOVA.loc['水準間']['平均平方和']=Sa/(a-1)
ANOVA.loc['残差']['平均平方和']=Ra/(n-a)
ANOVA['F値']=f
水準間の自由度は水準の数から1を引いて2、残差の自由度はデータの数から水準の数を引いて6となります。F分布表より、$F_{0.05}(2,6)=5.14$となり、F値は棄却域に入りません。よって、帰無仮説を採択する事になり、「1段目、2段目、3段目の売上に差があるとは言えない」となります。
どのように解けるか(解法)
今回は、ほぼ通常の分散分析の解法に従って解いたため、流れを沿う事にします。つまり、データから分散分析表の数値を埋める作業を挙げる事になります。まずは一般的な分散分析表の求め方の表を載せます。
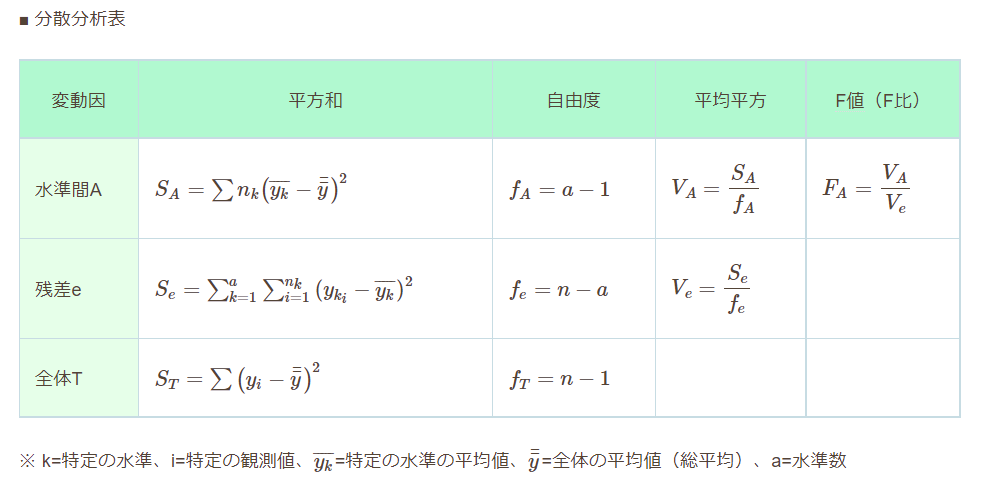
上記Pythonで行った手順
- 水準の自由度を求める(水準数-1)
- 残差の自由度を求める(全データ数-水準数)
- 水準間平均
- 全体の平均
- 水準間平方和
- 残差平方和
- 水準間の平均平方
- 残差の平均平方
- F値
これらを求めたら、水準の自由度と残差の自由度を用いてF分布表より臨界値を求めます。今回は臨界値より小さく、帰無仮説が採択されました。
参考
- とけたろう(2022.5)、一元配置分散分析【中学の数学からはじめる統計検定2級講座第16回】、Youtube
- @TaigaU121(2022.5)、Pythonで分散分析(対応なし・一元配置)、Qiita
- 自然科学の統計学、東京大学出版会
- Hidetosi SIRAI(2022.5)、Pythonで統計学を学ぶ(6)
- こちいにぃる(2022.5)、こちいにぃるの日記、【一元配置分散分析(One-way ANOVA)】、HatenaBlog:分散分析表の図
感想
今回、分散分析を始めて、いろいろ調べるのに時間をかけてしまいました。若い頃のツケが回ってきている事は百も承知ですが、社会にそれだけ浸透してない概念だとも言える気がします。統計検定2級の範囲をPythonで解ける様にするのが、まずの目的ではありますが、その実、パーリンノイズを理解して使いたいというのがあります。そのためにガウス分布を理解する必要があると思っていますが、丁度、統計検定2級が職場でトピックスになっていたのでそれと絡めました。パーリンノイズを理解して使える様にしつつ、統計から機械学習への繋がりも理解していきたいと考えています。
#次の記事
次回は、二元配置分散分析の予定です。