「近さ」をDeepLearningで表現して活用する研究があります。
画像などの高次元のデータから低次元のベクトルに落とし込んで、「距離を使って」人物の照合や類似画像検索などを行う方法です。代表的な論文として、ラベル情報無しで人の顔画像を精度良く分類するFacenetの論文と類似画像検索の論文を紹介します。
Reference
-
FaceNet: A Unified Embedding for Face Recognition and Clustering
- CVPR2015
-
Learning Fine-grained Image Similarity with Deep Ranking
- CVPR2014
文中の図表は論文より引用しています。
この記事は、Wantedlyの勉強会で取り上げられた論文・技術をまとめたものです。
2018年に読んだ機械学習系論文・技術まとめ at Wantedly Advent Calendar 2018 - Qiita
モチベーション
画像のクラス分類は、DeepLearningによって高精度で行うことができますが、「クラスに依らず同じものが写っているかどうか」を判定することは分類タスクにはできないことです。
この問題を解くために、画像を低次元(1000次元とか)ベクトルに変換し(Embedding)、そのベクトルの距離が近いものは「同じもの」だと学習するという方法があります。
この方法の面白いところは、明示的なクラスのラベルを必要としない点です。以下で見るように、同じペアか違うペアの画像を大量に用意することができれば学習が可能なところが魅力的な点です。
Facenet
顔の同一性判定は様々な用途があります。例えば、セキュリティーカメラや入退室管理、照合などがあげられます。選挙での重複投票を避けるために顔認識技術を使った国もあるそうです。
Facenetは、人間の顔を大量に集めて、「同じ人が写っている画像は照明や角度が変わっても距離が近い」ようなモデルを学習します。
モデルの構造は、画像をインプットにして比較的低次元(1000次元とか)の実数値ベクトルを出力します。二つの画像から得られた実数値ベクトルの距離が学習の対象です。
下の図が学習された画像間の距離の例です。ピクセルレベルでは上下の画像のほうが近いように見えます(どちらも横向き)が、実際は左右に同じ人の2枚が表示されています。
数値は学習された距離を表しており、同じ人同士の画像では向きが違くても相対的に近い距離になっています。この例では1.0付近を閾値にしたら同じ人・違う人が分けられそうです。(論文では1.1と言っています)

Triplet Loss
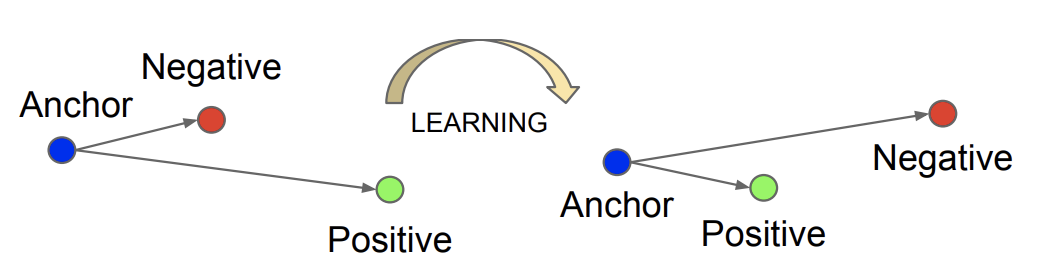
これを実現するための、損失関数がTriplet Lossです。
Triplet Lossでは、3枚の画像を必要とします。
- a: ランダムに選ばれた画像(anchor, 青)
- n: aと違う人物の画像 (negative, 赤)
- p: aと同じ人物の画像 (positive, 緑)
$f(x)$は画像xをネットワークに通したときに得られるベクトルで(絶対値が1になるように正規化されている)、二つの画像の距離は以下で与えられます。
$$
dist(x,y) = ||f(x) - f(y)||^2_2
$$
Triplet Lossの意図を意訳すると、「同じ人のペアより、違う人のペアの方が距離が小さいと言ったらペナルティ。しかもマージン$\alpha$だけちょっと厳しい」というものです。
$$
Loss = \sum^N_i [ dist(a, p) - dist(a, n) + \alpha ]_+
$$
逆に言うと、人のラベルはわからなくても同じか違うかのペアだけがあればこのロス関数は計算できます。
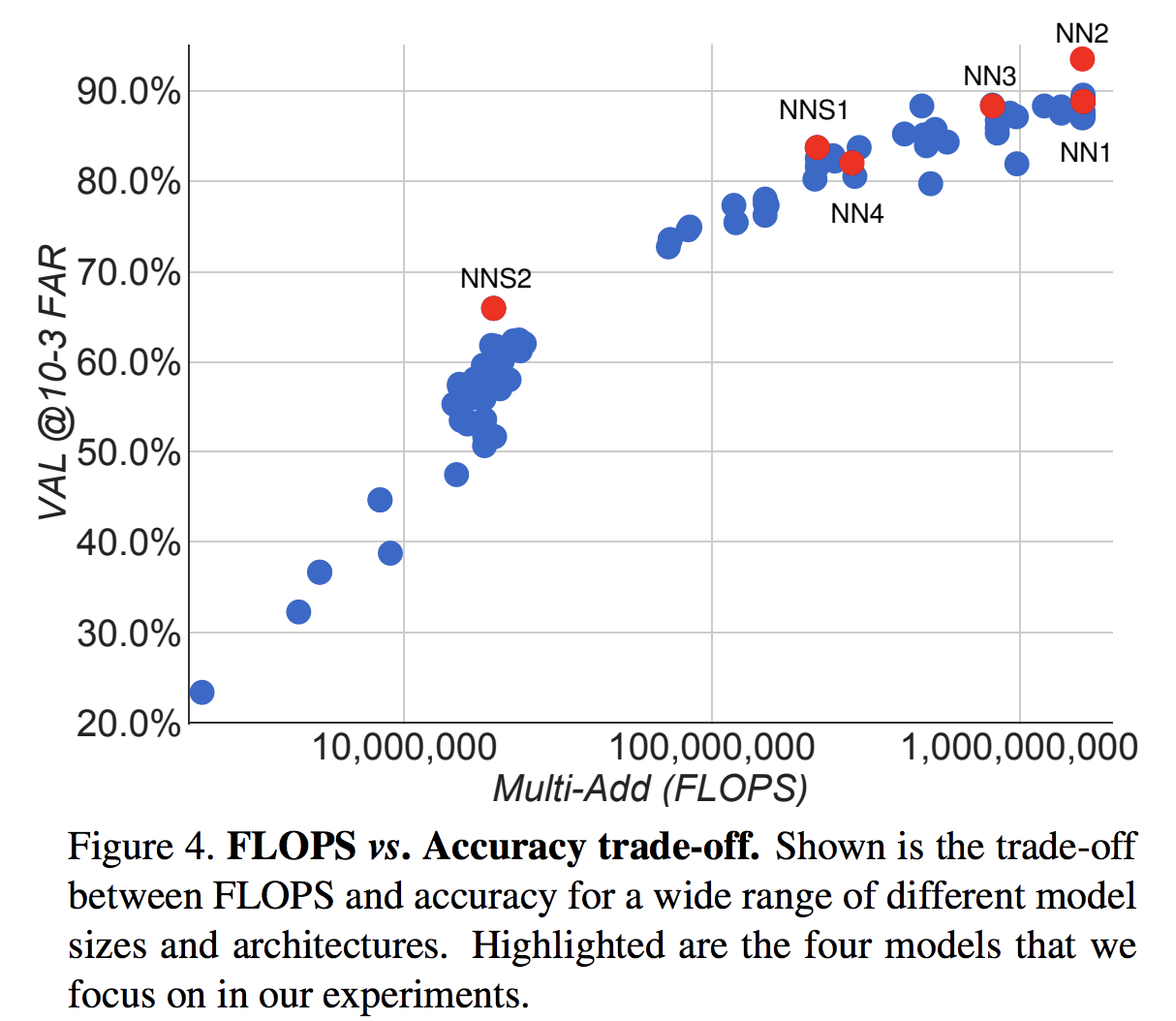
またベースとして使うネットワークは何でもいいので、精度と計算量のトレードオフを選択することが可能です。ネットワークの計算量(横軸)と綺麗な相関があるようです。
古典的な画像処理手法との比較
顔照合の問題とは離れますが、古典的な画像処理の特徴量ベースの画像類似度と比較していた例として Learning Fine-grained Image Similarity with Deep Ranking があります。
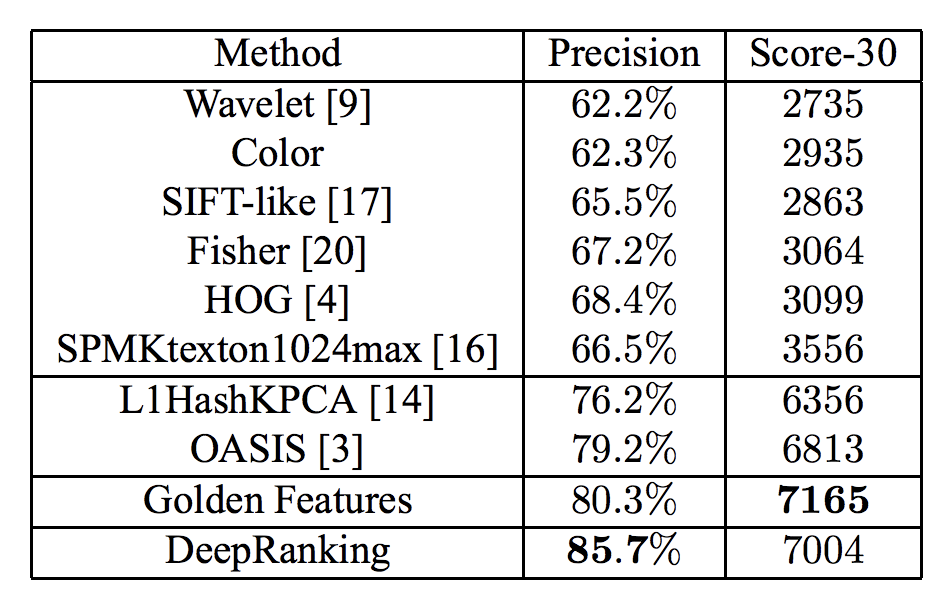
ここでは、古典的な画像処理の特徴量(SIFTとかHOGとか)ベースと比べて、画像の類似度の精度を評価しています。
人手の特徴量SIFT-likeとかHOGとか:70%前後に対して、DeepRankingでは精度が大きく向上しています。
まとめ
「似た画像を探す」や「同一の人物が写っているかどうかを判定する」という問題を、「画像からベクトルを出す」+「現実問題の関係とベクトル間の距離を近づける」という問題にすりかえたところがこれらの研究の好きなところです。
また、枠組みは画像だけでなく音声や言語にも使えるため応用が数多く考えられます。