概要
- Jupyter Notebook: https://github.com/tamuhey/python_1d_dft
- 第一原理計算の勉強がてら Python コードを書いた
- 1 次元調和振動子の Kohn-Sham 方程式を解くことを目指す
何を計算するか
- 1 次元調和振動子について,下のハミルトニアンの固有値問題を解く
$$\hat{H}=-\frac{1}{2}\frac{d^2}{dx^2}+v(x)$$
$$v(x)=v_{Ha}(x)+v_{LDA}(x)+x^2$$
微分作用素の行列表現
- まずは運動項$\frac{d^2}{dx^2}$の行列表現を求める
1階微分
$$(\frac{dy}{dx})_{i}=\frac{y _{i+1}-{y _{i}}}{h}$$
とするなら
$$D_{ij}=\frac{\delta_{i+1,j}-\delta_{i,j}}{h}$$
とすれば
$$(\frac{dy}{dx}) _ {i}=D_{ij} y _{j}$$
と書ける.(ただし端は定義できない)
$\delta_{ij}$はクロネッカーのデルタで,第 3 式はアインシュタイン縮約を用いている
実装
n_grid = 200
x = np.linspace(-5, 5, n_grid)
h = x[1] - x[0]
D = -np.eye(n_grid) + np.diagflat(np.ones(n_grid-1), 1)
D /= h
2 階微分
上と同じようにして
$$D^2_{ij}=\frac{\delta_{i+1,j}-2\delta_{i,j}+\delta_{i-1,j}}{h^2}$$
これは 1 階微分演算子を用いて下のように書ける(転置に注意).
$$D^2_{ij}=-D_{ik}D_{jk}$$
(ただし端を適当に処理する必要がある)
実装
- 2 行で書ける(!)
D2 = D.dot(-D.T)
D2[-1, -1] = D2[0, 0] # 端を処理
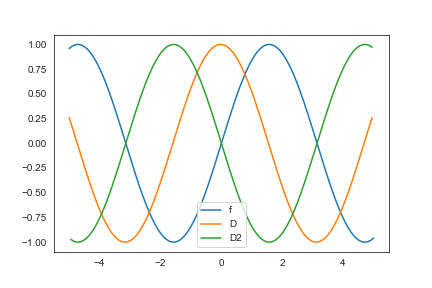
- 以下のように適当に sin カーブを微分してみると面白いかもしれません
y = np.sin(x)
plt.plot(x, y, label="f")
# 微分して端を落とす
plt.plot(x[:-1], D.dot(y)[:-1], label="D")
plt.plot(x[1:-1], D2.dot(y)[1:-1], label="D2")
plt.legend()
調和振動子のポテンシャル項
- 調和振動子のポテンシャル項$v_{ext}=x^2$を導入する:
$$\hat{H} = \hat{T} = - \frac{1}{2} \frac{d^2}{dx^2} + x^2$$
$v_{ext}(x)$の行列表現を$X$とする.
これは対角行列とすればよい.(1 行で書ける!)
X = np.diagflat(x**2)
解を求めてみる
- 上の2つの項を合わせれば,相互作用のない 1 次元調和振動子の波動関数を求める事ができる
eig_harm, psi_harm = np.linalg.eigh(-D2/2+X)
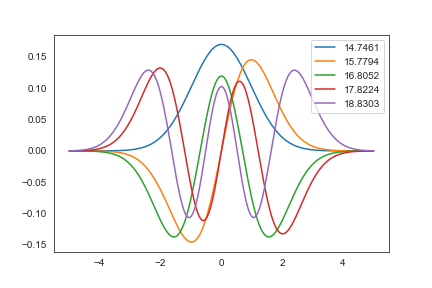
- 試しにエネルギーの低い方から 5 つプロット
for i in range(5):
plt.plot(x, psi_harm[:, i], label=f"{eig_harm[i]:.4f}")
plt.legend(loc=1)
電子密度
-
クーロン,ハートリー相互作用や LDA 交換項を入れたいが,これらは密度の汎関数
-
なのでまずは density を考える
-
このとき,波動関数の規格化条件を考える必要がある:
$$\int \lvert \psi \rvert ^2 dx = 1$$ -
occupation numbers を$f_n$とおけば,density $n(x)$は:
$$n(x)=\sum_n f_n \lvert \psi(x) \rvert ^2$$ -
電子は各状態につき 2 つまで入ることができる(スピン)
実装
def integral(x, y, axis=0):
dx = x[1] - x[0]
return np.sum(y*dx, axis=axis)
def get_nx(num_electron, psi, x):
# 規格化
I = integral(x, psi**2, axis=0)
normed_psi = psi / np.sqrt(I)[None, :]
# occupation num
fn = [2 for _ in range(num_electron // 2)]
if num_electron % 2:
fn.append(1)
# density
res = np.zeros_like(normed_psi[:, 0])
for ne, psi in zip(fn, normed_psi.T):
res += ne*(psi**2)
return res
Exchange energy
- 交換相互作用について考える (電子相関は面倒なので今回はパス)
- local density approximation (LDA) を用いると,以下のような汎関数となる:
$$E_X^{LDA}[n] = -\frac{3}{4} \left(\frac{3}{\pi}\right)^{1/3} \int n^{4/3} dx$$
- potential はこれを n によって微分することで求まる:
$$v_X^{LDA}[n] = \frac{\partial E_X^{LDA}}{\partial n} = - \left(\frac{3}{\pi}\right)^{1/3} n^{1/3}$$
実装
def get_exchange(nx, x):
energy = -3./ 4 * (3./np.pi) ** (1./3) * integral(x, nx**(4./3))
potential = -(3./np.pi) ** (1./3) * nx**(1./3)
return energy, potential
coulomb potential
-
1 次元の場合,3 次元の表式をそのまま用いると発散してしまうので,ちょっとずるして以下のように定義する
$$E_{Ha}=\frac{1}{2}\iint \frac{n(x)n(x')}{\sqrt{(x-x')^2+\varepsilon}}dxdx'$$- ただし$\varepsilon$は正の適当に小さい定数 -
ポテンシャルは n で微分して:
$$v_{Ha}=\int \frac{n(x')}{\sqrt{(x-x')^2+\varepsilon}}dx'$$
実装
def get_hatree(nx, x, eps=1e-1):
h = x[1] - x[0]
energy = np.sum(nx[None, :] * nx[:,None] * h**2 / np.sqrt((x[None, :]-x[:, None])**2 + eps) / 2)
potential = np.sum(nx[None, :] * h / np.sqrt((x[None, :]-x[:, None])**2 + eps), axis=-1)
return energy, potential
- 以上で今回欲しいハミルトニアンは定義できた
Kohn-Sham 方程式を解く:Self-consistency loop
- KS 方程式をときたいが,相互作用のない場合のように一発では解けない
- なぜなら,波動関数を求めたいが,ハミルトニアンの中に入っている電子密度は波動関数から導かれているから(循環参照!)
- なので self-consistency loop で解く:
- density を適当に初期化
- 交換項,クーロン項を求める
- ハミルトニアンを求める
- 波動関数と固有値を求める
- 収束判定を満たしていない場合,density を計算して 2. へ
- つまり入力と出力が等しくなるまで(self-consistent になるまで)ループを回し続ける
# max_iter回計算しても収束していなければ失敗
max_iter = 1000
# エネルギーの変化がenergy_tolerance以下ならば収束とする
energy_tolerance = 1e-8
# 電子密度初期化
nx = np.zeros(n_grid)
for i in range(max_iter):
# ポテンシャルを求める
ex_energy, ex_potential = get_exchange(nx, x)
ha_energy, ha_potential = get_hatree(nx, x)
# Hamiltonian
H = -D2 / 2 + np.diagflat(ex_potential+ha_potential+x**2)
# 波動関数を求める
energy, psi = np.linalg.eigh(H)
# 収束判定 -> もし収束していればおわり
if abs(energy_diff) < energy_tolerance:
print("converged!")
break
# 電子密度を更新する
nx = get_nx(num_electron, psi, x)
else:
print("not converged")
- 収束したら,
psiやnxをプロットすると面白いかも
Jupyter Notebook
動機
- DFTの勉強をしたくてこのdocumentを見つけたのですが,コードが書かれていなかったので書いてみました.