10 のメジャーな組合せ最適化問題における QUBO 行列生成コードの実装

概要

• メジャーな組合せ最適化問題（Set Partitioning, Graph Coloring 等）の QUBO 行列生成コードを実装した
• 参考：A Tutorial on Formulating and Using QUBO Models(本文中の引用はすべてこの資料から)
• この記事の JupyterNotebook はこちら -> GitHub

準備

• requirements
  • python>=3.7
  • dwave_qbsolv
  • networkx

from __future__ import annotations
from itertools import combinations
from dwave_qbsolv import QBSolv
from typing import Set, Tuple, Container, Dict, Sequence
from dataclasses import dataclass
import networkx as nx

• qubo 行列はnp.ndarrayで表すことにする
• しかし dwave_qbsolv に渡すにはdictにする必要があるので，helper function を用意しておく

def to_dict(q: np.ndarray) -> Dict[Tuple[int, int], float]:
    """Returns q matrix in the form of dict from np.ndarray

    The dict can be directly passed to dwave_qbsolv.QBSolv
    """
    assert len(q.shape) == 2 and  q.shape[0] == q.shape[1]
    return dict(zip(zip(*np.nonzero(q)), q[q!=0]))

• test code

def test_to_dict():
    q = np.array([[1,2],
                  [2,4]])
    assert to_dict(q) == {(0,0):1, (0,1):2, (1,0):2, (1,1):4}
test_to_dict()

• np.ndarrayの QUBO 行列から解を得る function も用意しておく

def qbsolv_from_ndarray(q: np.ndarray) -> Tuple[np.ndarray, np.ndarray]:
    """Returns lowest energy samples from dwave qbsolv.(for test util)"""
    res = QBSolv().sample_qubo(to_dict(q)).record
    i = res.energy == res.energy.min()
    return res.sample[i], res.energy[i]

The Number Partitioning Problem

• Partition problem - Wikipedia
• 数の集合を 2 つに分割したとき，それぞれの和が一致するような分け方はあるか？
• 集合の要素に qubit を$x_{i}$を割り当てる
  • 分割後の集合 k に入る場合は$x_{i}=k$

def qubo_number_partition(number_set: Container[float]) -> np.ndarray:
    """Return Q matrix of number partitioning problem

    Math:
        q_{ii} = s_{i}(s_{i}-c) \\
        q_{ij} = q_{ji} = s_{i}s_{j} \\
        c = \sum_i{s_{i}}
    """
    number_set = np.array(list(number_set))
    c = number_set.sum()
    q = np.outer(number_set, number_set)
    np.fill_diagonal(q, number_set*(number_set-c))
    return q

• test

def test_qubo_number_partition():
    s = np.array([3,1,1,2,2,1])
    sample, _ = qbsolv_from_ndarray(qubo_number_partition(s))
    assert s[sample[0] == 1].sum() == 5
    assert s[sample[0] == 0].sum() == 5
test_qubo_number_partition()

The Max-Cut Problem

• https://en.wikipedia.org/wiki/Maximum_cut
• 先程と同じく，各ノードに対して qubit を割り当て，2 つの集合に分けることを考える
• エッジ(i,j)に対して，$(x_{i}-x_{j})^2=1$のとき，$(i,j)$がカットに含まれることを利用する
• 後々グラフを扱う問題がいくつか出てくるので，Graph Class を用意する
  • データ形式のチェックなどはこれに任せる．（とりあえずは最低限のチェックのみ実装する）
  • networkx とのやり取り機能をつけておく

@dataclass
class Graph:
    edges: Collection[Collection[int]] # edge is represented as (i, j)
    n_nodes: int
    init_value: Mapping[int, int] = None # init_value[i] indicates init value of node i
    nodes: Sequence[float] = None # value of nodes. len(nodes) must be n_nodes

    def __post_init__(self):
        if self.nodes is not None: assert len(self.nodes) == self.n_nodes
        if self.edges is None: return
        if len(self.edges) == 0:
            self.edges = None
            return
        self.edges = np.array(list(self.edges))
        assert self.edges.max() < self.n_nodes
        assert self.edges.shape[1] == 2
        if self.init_value is not None:
            assert all(np.array(list(self.init_value)) < self.n_nodes)

    @classmethod
    def from_networkx(cls, graph: nx.Graph) -> Graph:
        return cls(edges = graph.edges, n_nodes = graph.number_of_nodes())

    def to_networkx_graph(self) -> nx.Graph:
        nxg = nx.Graph()
        nxg.add_nodes_from(range(self.n_nodes))
        nxg.add_edges_from(self.edges)
        return nxg

• test

def test_graph():
    edges = {(1,2), (3,4)}
    graph = Graph(edges, 5)
    assert graph.edges.shape == (2,2)
    nxg = graph.to_networkx_graph()
    _graph = Graph.from_networkx(nxg)
    assert np.array_equal(graph.edges, _graph.edges)
    assert graph.n_nodes == _graph.n_nodes
test_graph()

• max-cut 実装

def qubo_max_cut(g: Graph) -> np.ndarray:
    n_nodes = g.n_nodes
    q = np.zeros((n_nodes, n_nodes))
    i, j = g.edges.T
    np.add.at(q, (i,i), -1)
    np.add.at(q, (j,j), -1)
    q[i,j] += 1
    q[j,i] += 1
    return q

• test
  • test 用の helper function を用意しておく

def is_contain(x: np.ndarray, y: np.ndarray) -> bool:
    """If y \in x"""
    assert len(x.shape) -1 == len(y.shape)
    return any(np.array_equal(xi, y) for xi in x)

def test_qubo_max_cut():
    edges = [(0,1), (0,2), (1,3), (2,3), (2, 4), (3, 4)]
    g = Graph(edges=edges, n_nodes=5)
    q = qubo_max_cut(g)
    assert q.tolist() == [[-2,1,1,0,0],
                          [1,-2,0,1,0],
                          [1,0,-3,1,1],
                          [0,1,1,-3,1],
                          [0,0,1,1,-2]]
    sample, _ = qbsolv_from_ndarray(q)
    assert is_contain(sample, np.array([0,1,1,0,0]))
test_qubo_max_cut()

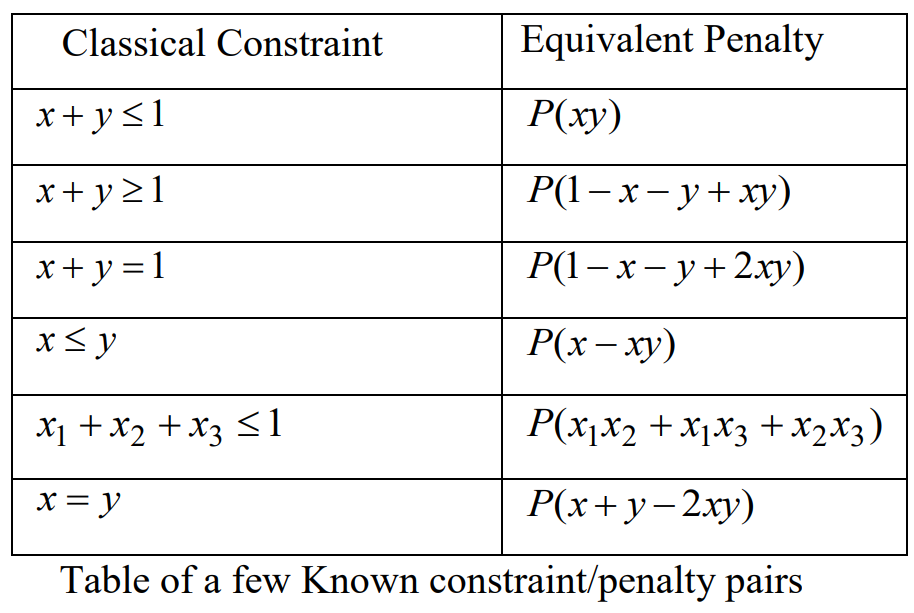
known penalties

• 上の 2 つのモデルは，制約式がなかったため非常に簡単に QUBO モデルにできた
• しかし制約がある場合はどうしたらよいか？一般的に下の表が役に立つ （引用：A Tutorial on Formulating and Using QUBO Models

The Minimum Vertex Cover Problem (MVC)

• Vertex cover - Wikipedia
• グラフのすべての枝について，端点の少なくとも一方が属するような頂点の部分集合を求める問題

def qubo_mvc(g: Graph, penalty: float = 10.):
    """The Minimum Vertex Cover Problem (MVC)

    Math:
        y = \sum_{j \in V}x_{j} + P\left(\sum_{(i,j) \in E}\left(1-x_{i}-x_{j}+x_{i}x_{j}\right)\right)
    """
    q = np.diagflat(np.ones(g.n_nodes))
    i, j = g.edges.T
    np.add.at(q, (i,i), -penalty)
    np.add.at(q, (j,j), -penalty)
    q[i,j] += penalty/2.
    q[j,i] += penalty/2.
    return q

• test

def test_qubo_mvc():
    edges = [(0,1), (0,2), (1,3), (2,3), (2, 4), (3, 4)]
    g = Graph(edges=edges, n_nodes=5)
    q = qubo_mvc(g, penalty=8.)
    sample,_ = qbsolv_from_ndarray(q)
    assert is_contain(sample, np.array([0,1,1,0,1]))
test_qubo_mvc()

The Weighted Minimum Vertex Cover Problem (W-MVC)

• MVC の重み付きバージョン

def qubo_wmvc(g: Graph, penalty: float = 10.):
    """The Minimum Vertex Cover Problem (MVC)

    Math:
        y = \sum_{j \in V}w_{j}x_{j} + P\left(\sum_{(i,j) \in E}\left(1-x_{i}-x_{j}+x_{i}x_{j}\right)\right)
    """
    q = np.diagflat(np.ones(g.n_nodes)*g.nodes)
    i, j = g.edges.T
    np.add.at(q, (i,i), - penalty*g.nodes[i])
    np.add.at(q, (j,j), - penalty*g.nodes[j])
    q[i,j] += penalty/2.
    q[j,i] += penalty/2.
    return q

• test
  • めんどいので重みは全部 1 にする

def test_qubo_wmvc():
    edges = [(0,1), (0,2), (1,3), (2,3), (2, 4), (3, 4)]
    g = Graph(edges=edges, n_nodes=5, nodes=np.ones(5))
    q = qubo_wmvc(g, penalty=8.)
    sample, _ = qbsolv_from_ndarray(q)
    assert is_contain(sample, np.array([0,1,1,0,1]))
test_qubo_wmvc()

Remarks about the scalar penalty P

Generally, there is a ‘Goldilocks region’ of considerable size that contains penalty values that work well. A little preliminary thought about the model can yield a ballpark estimate of the original objective function value. Taking P to be some percentage (75% to 150%) of this estimate is often a good place to start.

The Set Packing Problem

• Set packing - Wikipedia

def qubo_set_pack(a: np.ndarray, weight: np.ndarray, penalty=8.) -> np.ndarray:
    """Set Packing Problem

    Math:
        min\ \sum_{j=1}^n w_{j}x_{j} \\
        st \\
        \sum_{j=1}^n a_{ij}x_{j} \le 1
    """
    assert len(a.shape) == 2
    assert a.shape[-1] == len(weight)
    q = -np.diagflat(weight)
    c = np.einsum("ij,ik->ijk",a,a).astype(np.float) / 2. # constraint
    c *= (1 - np.eye(a.shape[-1]))[None,...] # zeros diag
    q += penalty*c.sum(0)
    return q

• test

def test_qubo_set_pack():
    a = np.array([[1,0,1,1],
                  [1,1,0,0]])
    w = np.ones(4)
    q = qubo_set_pack(a, w, penalty=6.)
    assert q.tolist() == [[-1,3,3,3],
                         [3,-1,0,0],
                         [3,0,-1,3],
                         [3,0,3,-1]]
    assert is_contain(qbsolv_from_ndarray(q)[0], np.array([0,1,1,0]))
test_qubo_set_pack()

The Max 2-Sat Problem

• Boolean satisfiability problem - Wikipedia
• 面白いことに，Clause の数によらないモデルとなる
• Clause のデータ型を定義しておく
  • リテラルが否定なら sign = False

@dataclass
class Clauses:
    literals: np.ndarray[int]
    signs: np.ndarray[bool]
    def __post_init__(self):
        assert len(self.literals) == len(self.signs)

• 実装

def qubo_max2sat(c: Clauses):
    n = c.literals.max()+1
    q = np.zeros((n,n))
    i,j=c.literals.T
    si,sj=c.signs.T
    np.add.at(q, (i[sj], i[sj]), ((-1)**si)[sj])
    np.add.at(q, (j[si], j[si]), ((-1)**sj)[si])

    offdiag=np.zeros_like(q)
    np.add.at(offdiag, (i,j), (-1)**(si^sj) / 2.)
    return offdiag + offdiag.T + q

• test

def test_qubo_max2sat():
    l = np.array([[0,1],[0,1],[0,1],[0,1],[0,2],
                  [0,2],[1,2],[1,3],[1,2],[1,2],
                  [2,3],[2,3]])
    s = np.array([[True,True],[True,False],[False,True],[False,False],
                  [False,True],[False,False],[True,False],[True,True],
                  [False,True],[False,False],[True,True],[False,False]])
    q = qubo_max2sat(Clauses(l,s))
    assert q.tolist() == [[1,0,0,0],
                          [0,0,-0.5,0.5],
                          [0,-0.5,0,1],
                          [0,0.5,1,-2]]
    sample, _ = qbsolv_from_ndarray(q)
    assert is_contain(sample, np.array([0,0,0,1]))
test_qubo_max2sat()

The Set Partitioning Problem (SPP)

• Partition of a set - Wikipedia
• この問題では qubit は集合の要素ではなく，部分集合を表す
• SPP はクラスタリングともみなすことができ，機械学習との関連が資料の中で紹介されている

def qubo_spp(cost: np.ndarray, set_flag: np.ndarray, p=10.):
    """The Set Partitioning Problem (SPP)

    Args:
        set_flag: 2-rank array. (i,j) = 1 if element i in set j.
    """
    assert cost.shape[0] == set_flag.shape[1]
    b = np.ones(set_flag.shape[0])
    return np.diagflat(cost - p*2*b.dot(set_flag))  + p*np.einsum("ij,ik->jk",set_flag,set_flag)

• test

def test_qubo_spp():
    c = np.array([3,2,1,1,3,2])
    a = np.array([[1,0,1,0,0,1],
                  [0,1,1,0,1,1],
                  [0,0,1,1,1,0],
                  [1,1,0,1,0,1]])

    q=qubo_spp(c, a)
    assert q.tolist() == [[-17,10,10,10,0,20],
                        [10,-18,10,10,10,20],
                        [10,10,-29,10,20,20],
                        [10,10,10,-19,10,10],
                        [0,10,20,10,-17,10],
                        [20,20,20,10,10,-28]]
    sample, _ = qbsolv_from_ndarray(q)
    assert is_contain(sample, np.array([1,0,0,0,1,0]))
test_qubo_spp()

Graph Coloring

• Graph coloring - Wikipedia
• 応用範囲が広い
  • スケジューリング，基板デザイン，レジスタ割付
  • 以前数独の実装をした
• ノード i が色 j で塗られるとき，qubit を 1 とする
  • つまり見通しを良くするために，qubit は行列で，qubo 行列は 4 階の ndarray で表現する

def qubo_graph_coloring(g: Graph, n_color, penalty=10.) -> np.ndarray:
    """Graph Coloring"""
    n = g.n_nodes
    q=np.zeros((n,n_color,n,n_color))

    # each nodes are colored by one color
    i=range(n)
    q[i, :, i, :] = penalty*(np.ones((n_color,n_color)) - 2*np.eye(n_color))

    # adjacent nodes are not colored with same color
    i, j = g.edges.T[...,None]
    k=range(n_color)
    q[i,k,j,k]+=penalty/2.
    q[j,k,i,k]+=penalty/2.

    return q.reshape(n*n_color,n*n_color)

def test_qubo_graph_coloring():
    edges = [[0,1],[0,4],[1,2],[1,3],[1,4],[2,3],[3,4]]
    n_nodes, n_color=5, 3
    g = Graph(edges=edges, n_nodes=n_nodes)
    ans=np.zeros(n_nodes*n_color)
    ans[[1,3,8,10,14]]=1
    q=qubo_graph_coloring(g, n_color, penalty=4.)
    assert is_contain(qbsolv_from_ndarray(q)[0],ans)
test_qubo_graph_coloring()

ちなみに

This approach to coloring problems has proven to be very effective for a wide variety of coloring instances with hundreds of nodes.

らしい.n_color 色に対して n_color qubit を用意しているが，log_2(n_color)ですむような構成法はないか？

General 0/1 Programming

Many important problems in industry and government can be modeled as 0/1 linear programs with a mixture of constraint types.

• 不等式制約を slack 変数の導入によって QUBO に入れている点が面白い

def qubo_general01(cost, a, b, sign, penalty=10.):
    """General 0/1 Programming

    Args:
        a, b: constraint (ax=b)
        sign: 0 is equality, 1 is >=, -1 is <=
    """
    slack = - sign * b
    slack[sign==0] = 1.
    slack[sign == 1] += a[sign==1,:].sum()
    slack = np.ceil(np.log2(slack)).astype(np.int)

    ni = a.shape[0]
    for i, ns in enumerate(slack):
        if ns:
            t = np.zeros((ni,ns))
            t[i] = -sign[i]*2**np.arange(ns)
            a=np.concatenate([a,t],-1)

    return - np.diagflat(np.concatenate([cost, np.zeros(sum(slack))])+2*penalty*b.dot(a)) + penalty*np.einsum("ij,ik->jk",a,a)

• test

def test_qubo_general01():
    c = np.array([6,4,8,5,5])
    a = np.array([[2,2,4,3,2],
                  [1,2,2,1,2],
                  [3,3,2,4,4]])
    b = np.array([7,4,5])
    s = np.array([-1,0,1])
    q=qubo_general01(c,a,b,s)
    sample, _=qbsolv_from_ndarray(q)
    assert is_contain(sample[:,:5], np.array([1,0,0,1,1]))
test_qubo_general01()

Quadratic Assignment Problem (QAP)

• Quadratic assignment problem - Wikipediak
• 工場の配置などに応用できる

def qubo_qap(flow:np.ndarray, distance: np.ndarray, penalty=10.):
    """Quadratic Assignment Problem (QAP)"""
    n = len(flow)
    q = np.einsum("ij,kl->ikjl",flow, distance).astype(np.float)

    i = range(len(q))
    q[i,:,i,:] += penalty
    q[:,i,:,i] += penalty
    q[i,i,i,i] -= 4*penalty
    return q.reshape(n**2,n**2)

def test_qubo_qap():
    flow = [[0,5,2],
            [5,0,3],
            [2,3,0]]
    distance = [[0,8,15],
                [8,0,13],
                [15,13,0]]
    q = qubo_qap(flow, distance, penalty=200.)
    sample, _ = qbsolv_from_ndarray(q)
    assert is_contain(sample, np.array([1,0,0,0,1,0,0,0,1]))
test_qubo_qap()

Quadratic Knapsack Problem (QKP)

• 2 次のナップサック問題
• 以下で見るように，コスト制約のもと遂行するプロジェクトを決定するなどの応用ができる

widespread application in such areas as project selection and capital budgeting.

In such settings, a set of attractive potential projects is identified and the goal is to identify a subset of maximum value (or profit) that satisfies the budget limitations.
The quadratic version of this problem arises when there is an interaction between pairs of projects affecting the value obtained.

def qubo_qkp(value:np.ndarray, a:np.ndarray, b:float, penalty=10.) -> np.ndarray:
    """Quadratic Knapsack Problem (QKP)"""
    n = len(value)
    nslack = np.ceil(np.log2(b))
    slack = 2 ** (np.arange(nslack))
    a = np.concatenate([a,slack])
    q = penalty*(np.outer(a,a) - 2*b*np.diag(a))
    q[:n,:n] -= value
    return q

def test_qubo_qkp():
    value = np.array([[2,4,3,5],
                      [4,5,1,3],
                      [3,1,2,2],
                      [5,3,2,4]])
    a = np.array([8,6,5,3])
    b = 16
    q = qubo_qkp(value, a, b, penalty=10.)
    sample, _ = qbsolv_from_ndarray(q)
    n = len(a)
    assert is_contain(sample[:,:n], np.array([1,0,1,1]))
test_qubo_qkp()

The QUBO approach to QKP has proven to be successful on problems with several hundred variables and as many as five knapsack constraints.

おわりに

• 参考：A Tutorial on Formulating and Using QUBO Models(本文中の引用はすべてこの資料から)
• この記事の JupyterNotebook はこちら -> GitHub
  • ライブラリ化したのでpipで入れられます