PythonでNFA（非決定性オートマトン）を実装し、例の曲を判定する

これは ZOZO Advent Calendar 2022 カレンダー Vol.5 の 10 日目の記事です。
昨日の投稿は @rayuron さんの「AIが音楽に変える！「text2music」でツイートから音楽を作ってみよう」でした。

ZOZO Advent Calendar 2022 をご覧のみなさん、こんにちは。
ZOZO ML・データ部所属の @tama_Ud です。

前回はPythonでDFAを実装しましたが、今回はNFAのシミュレータを実装したいと思います。

NFAとは

まずは有限オートマトン (finite automaton) についておさらいです。

有限オートマトンは有限個の状態と遷移と動作の組み合わせからなる数学的に抽象化された「ふるまいのモデル」- Wikipedia

構文解析、アプリケーションの動作のモデリング、自然言語のモデル化などによく利用されます。
馴染みがないように聞こえるかもしれませんが、設計書などでUMLによる状態遷移図を見たことがある方はいらっしゃるのではないでしょうか。
正規表現エンジン実装にも使われる計算機モデルなので、知らずとみなさん (grepコマンド等で) お世話になっているはず。

NFAの「非決定性」

有限オートマトンの分類法はいくつかありますが、この記事では前回に引き続き「決定性」に注目します。
有限オートマトンは、「決定性」の性質の有無によって以下の2つに分類できます。

1. 決定性有限オートマトン (DFA) : 状態と入力によって次に遷移すべき状態が一意に定まる
2. 非決定性有限オートマトン (NFA) : ある状態と入力があったとき、次の遷移先が一意に決定しないことがある

NFAの5つ組

定義自体はシンプルなので、形式的な説明から書いておきます。
非決定性有限オートマトン（以下NFA）も、決定性有限オートマトン（以下DFA）と同様、以下の５つ組で定義されます。

• $\varrho : 状態集合$　
• $\sum : 入力アルファベット$
• $\delta : \varrho \times \sum_\varepsilon からP(\varrho)への遷移関数 (状態と入力を受け取り、状態を返す) $
• $q_0 : 開始状態 (q_0 \in \varrho)$
• $F : 受理状態の集合 (F \subseteq \varrho)$
  $集合\varrho, \sum, Fはいずれも有限集合$
  $\sum_\varepsilonは\sum \cup \{\varepsilon\}$
  $P(\varrho)は\varrho$の冪集合（すべての部分集合の集まり、空集合を含む）

DFAとほとんど同じですが、入力に文字列または空列を受け取ります。
また、$\delta$の遷移先は$P(\varrho)$となります。

受理状態の定義

$M = (\varrho, \sum, \delta, q_0, F)$ をNFA
$y_i \in \sum_\varepsilon$
$\omega = y_1y_2...y_m$ を$\sum$ 上の長さ $n$ の文字列とする ($\omega \in \sum^n$)
$M$が$\omega$を受理するとは、状態の列$r_1,r_2...,r_m \in \varrho$ が存在する場合、次を満たすことです。

1. $r_0 = q_0$
2. $i = 0, ..., m-1$の時, $r_{i+1} \in \delta(r_i,y_{i+1})$（）
3. $r_m \in F$

NFAとDFAの等価性

NFAとDFAは同じ言語のクラスを認識します（等価）。
また、NFAはDFAよりも簡潔に書けることがあります。これは実際に状態遷移図を書いてみるとわかりやすいと思います。

有限オートマトンと正規表現

今回の実装では有限オートマトンを正規表現で記述しますので、最初になぜ記述できるのかを説明しておきます。
コードを読んでから戻ってきた方がわかりやすいかもしれませんね。

正規表現とは、文字列の集合を一つの文字列で表現する方法の一つです。 (Wikipedia)
そして、「有限オートマトンで受理可能な言語」は「正規言語」と定義されます。
「正規表現」と「有限オートマトン」は記述能力において等価 (相互変換可能、同一の正規言語を記述可能) なので、マッチングパターンを正規表現で記述できるんですね。

等価性やFAと正規表現の相互変換方法についてはこちらのスライドを参考にしました。
参考: Note3 正規表現 - 形式言語とオートマトン

正規表現と演算

定理: 正規言語は、3つの演算、(1)和集合、(2)連接、(3)閉包について閉じている (閉性がある)。
よって、任意の正規言語にこの3つの演算を行なっても正規言語のままである。

こちらの定理も、コードを読んでから読むと恩恵をめちゃくちゃ感じられると思います。

有限オートマトンは他の演算にも閉性を持っていますが、この記事では割愛します。
閉性の証明はこちらのスライドがまとまっています。
参考: 6. 正規⾔語の閉性 - 形式言語理論

こちらの書籍も参考にしました。
図とコンセプトの理解を中心とした証明が豊富で、概要の理解に最適でした。
参考: 計算理論の基礎

GNFA

さらにGNFAについても (形式的な説明にとどめますが)、触れておきます。

GNFA (拡張非決定性有限オートマトン) とは、たは拡張非決定性有限状態機械とは、各状態遷移が任意の正規表現に対応する NFA である。GNFA は入力からまとめて複数の文字を読み込むが、その文字列は遷移（エッジ）に付記された正規表現に対応するものである。 - Wikipedia
Generalized nondeterministic finite automaton - Wikipedia (英語)

有限オートマトンでは、入力文字一文字に対して一つの遷移しか行えませんが、GNFAはこの制限を緩和 (拡張) したものです。
GNFAは正規表現に簡単に変換できます。

NFA ⇄ GNFA ⇄ 正規表現の変換

正規表現をNFAに変換するために、今回はよく知られた手法であるThompson法を使います。
状態数が正規表現文字列の長さに等しいのが特徴です。

参考: Regular Expression Search Algorithm

実装

0. 実装方針

今回もPythonで実装していきます。
Thompson法で正規表現からNFAを構築し、Wu-Manberのビットパラレル手法を利用してシミュレートしてみます。

1. NFAの定義

今回は5つ組でなく、正規表現でNFAを定義します。

nfa.py

# NFAシミュレータの定義
T = "cccccababababccccc" # 検索対象文字列
P = "abababab|ababab|abab"  # [pattern (キーワード) -> 正規表現 -> 構文木] -> Thompson-NFA
subpattern = re.split("[・|*]", P) # サブパターンを演算子で分割する
s = len(subpattern)  # サプパターンの個数
n = len(T)  # 検索対象文字列の長さ
S = frozenset(("a", "b", "c"))  # 入力文字の集合
M = [{s_alpha: 0 for s_alpha in S} for _ in subpattern] # マスクビット初期化　{ 各入力文字 : 0で初期化=0b000000.. }

abababab,ababab,ababの3つをキーワードとし、正規表現で記述したものが変数Pです。

P = "abababab|ababab|abab"

本来の表記とは異なるのですが、簡単のため "|" のみを用いて記述しました。
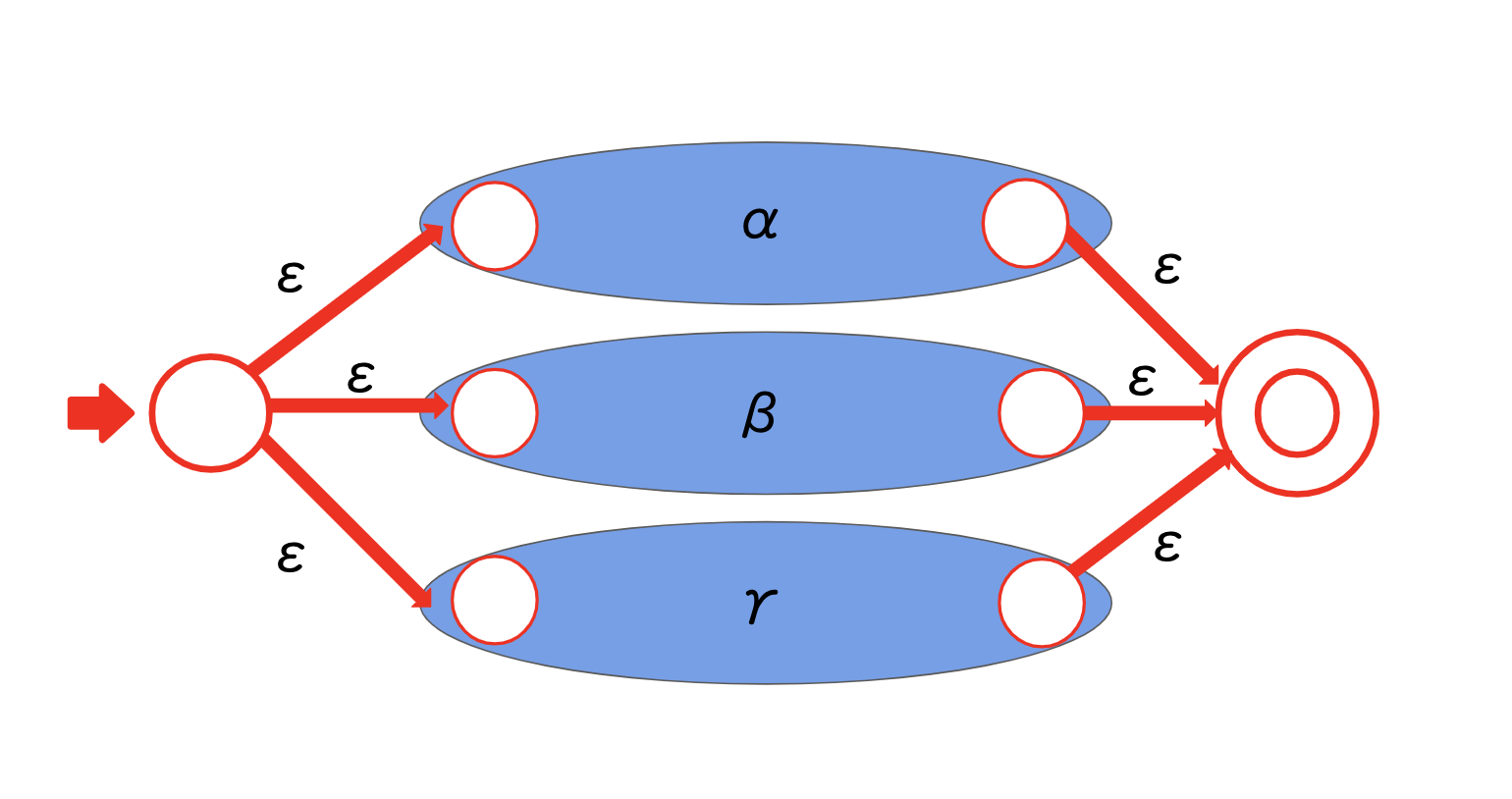
Thompson-NFAの構築法を参考に、正規表現からNFAを構築します。

ε遷移で選択を表現しています。("・","*" も表現できます。前述のスライドをご参考にしてください。)
"|"(選択)はOR演算(和集合)として表現できます。
前述の閉包性から、正規言語の和集合も正規言語になるんでしたね。

2. 実行部分の定義

今回は遷移関数の定義はありません。
Shift-And法 (ビット演算) でNFAシミュレーションを行います。
Wu-Manberのビットパラレル手法を参考にしました。

bit-parallel-nfa-simulator.py

# ビットパラレル化によるNFAシミュレーション (Shift-And法) 
def bitparallelThompsonNfa():
    #### マスクビット作成 ####
    for i in range(s):
        temp = 1  # bitを立てた状態で初期化
        for sub_a in subpattern[i]:
            M[i][sub_a] |= temp
            temp <<= 1

    #### マッチング ####

    # 0b100000のように左端のビットを立てる(受理状態).
    accept = [1 << len(sub)-1 for sub in subpattern]
    for i in range(s): # range(s)=サブパターンの個数
        R = 0
        for t_alpha in T: # T=対象検索文字列
            # << & (Shif,And) を使ったビット演算によるNFAのシミュレーション
            R = (((R << 1) | 1) & M[i][t_alpha])
            if (R & accept[i]) != 0:
                print(f'*** マッチしました {subpattern[i]} ***')
                return

エラー処理等は適宜追加してください。
コードはこちらです : GitHub

3. 実行

$ python3 bit-parallel-nfa-simulator.py
>> *** マッチしました abababab ***

(おまけ) NFAで例の曲を識別してみる

上記のスクリプトを使って、この3種類の文字列をマッチングしてみてください。

ドンドン -> ドンブラザーズ
ドンドンドン -> ドン・キホーテ
ドンドンドンドン -> ドン・グリス
※曲は適宜検索してください

終わりに

明日は @YasuhiroKimesawa さんの「バス係数とは？」です。
お楽しみに！

追記について追記

2023/04/09 内容を大幅に加筆修正しました。
オートマトンといえばCSの基礎の基礎というところですが、その広い応用範囲から汎用性の高さが窺えますね。
非常にシンプルな定義から始まり、コンセプトも明瞭なため初学者にも面白かったのですが、どこまで学んでも「本質から理解した感 (腹落ちした感?)」がなく、この短い記事を加筆するのに3ヶ月もかかってしましました。
加筆版を書き上げた今も空を掴んでいるような心持ちです。
他の領域を概観してから戻ってくるとまた新たな気づきがありそうな分野なので、今後も行きつ戻りつ学んでいこうと思います。

参考文献

論文

• Sun Wu, Udi Manber - Fast text searching: allowing errors
• Ken Thompson - Regular Expression Search Algorithm

書籍

• 新屋良磨，鈴木勇介，高田謙 - 正規表現技術入門
• Michael Sipser - 計算理論の基礎

講義スライド

• 情報知識ネットワーク特論「情報検索とパターン照合」
• Note3 正規表現 - 形式言語とオートマトン
• 6. 正規⾔語の閉性 - 形式言語理論