目的
ここでは、熱力学における熱平衡状態(単に平衡状態とも言います)のお話をします。
これを読むと熱力学という学問がどういった枠組みの中での理論なのかがわかっていただけると思います。
熱力学はある熱平衡状態から別の熱平衡状態への変化を示す学問
熱力学には、平衡系の熱力学と、非平衡系の熱力学があります。
非平衡系の熱力学は、まだ限られた状況でしか成り立たないので、まだ未完成の分野であります。
一般的に熱力学というと、前者の平衡系の熱力学のことを指します。
熱平衡状態や平衡状態という言い方をします。
ところで平衡系とはなんでしょうか。
雑な言い方をすれば、落ち着いた状態を平衡状態と言います。
例えば、下記のように中央に敷居がある箱を用意し、左側に多数の粒子を閉じ込めておきます。
右側は真空状態としておきます。
※この時に、箱は断熱材で熱の注入や逃げがないものとします。
敷居を取ると、当然左側にいた粒子が右側へ流れ込むでしょう。

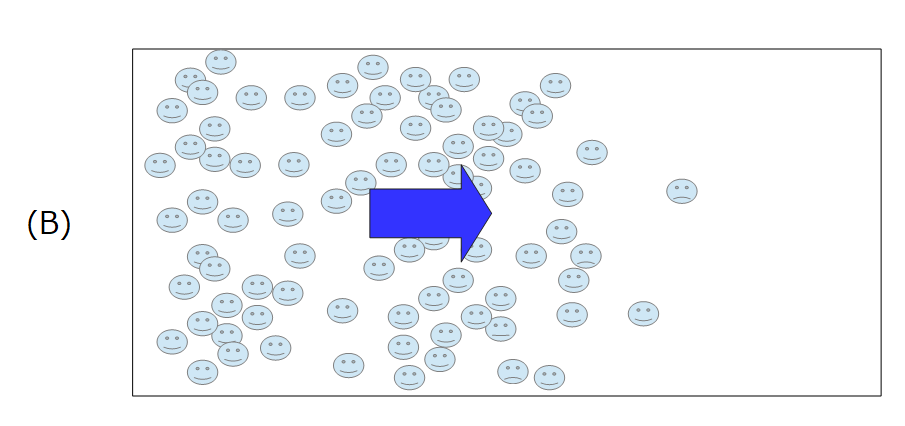
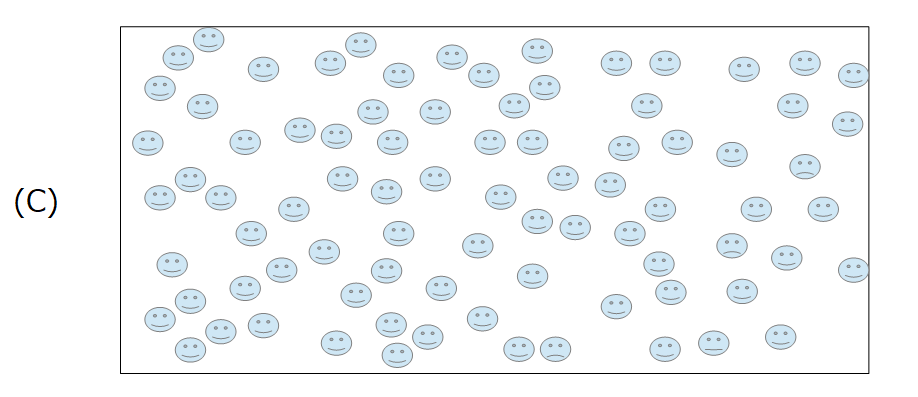
このように、初期状態を(A)として、(B)のような流れを生み、やがて(C)のようになり、状態としてはこれ以上動かなくなるでしょう。
大多数の粒子はある時間をかけて左から右側へ移動を起こして、やがておちついた状態へ行きます。
これがある平衡状態から別の平衡状態へ変わったという意味になります。
しかし、誤解をしてはいけません。
これは粒子が全く移動しなくなったという意味ではありません。
あくまでマクロな視点で見た時、マクロな変数である温度や圧力の変化が無くなったというだけで、個々の粒子は相変わらずあちこち飛び回っているのです。
つまり、平衡状態とは「マクロ変数が時間的に変化しない状態」、言い換えると**「マクロ状態が時間的に変化しない状態」**のことを言いますので、個々の粒子のがどの位置にいてどれだけの速度で運動しているかは問題にはしていません。
(もちろん気体分子運動論などではそれらの運動の平均として、マクロな状態を形成しているのですが)
熱力学では、上記のような(B)の表現をすっ飛ばして、(A)から(C)の変化がけを追って議論することになります。
なので、下記のような**平衡状態(A)から、別の平衡状態(C)についての変化について考えるのが、「熱力学という学問」**です。
(B)のような状態の変化は考慮しなくても良いのか
本当は、(B)のような詳細な変化があるのですから、忠実に(B)も考慮した議論というのもした方が良いのではないかという疑問が残ります。
しかし、(B)のような別の平衡状態へ向かう過程を考慮するかどうかは、その時間スケールが見たい時間スケールに比べて考慮しなければならないかどうかによると考えられます。
例えば、(A)から(C)へ向かう過程の時間が$\Delta \tau$であったとします。
そして、見たい時間刻みのスケールが$\Delta t$であるとすると、
$\frac{\Delta \tau}{\Delta t}$の大きさが大きいか小さいかが重要になります。
(1)$\frac{\Delta \tau}{\Delta t}→0$のとき
これは見たい時間スケール$\Delta t$に対して、(A)から(C)へ向かう過程の時間が$\Delta \tau$がとても小さいということを意味しています。
つまり、(A)から(C)への変化は一瞬で起こるのですから、(B)のような仮定を考慮する必要は全くないということになります。
数値計算で考えればわかりやすいでしょうか。
数値計算では、有限のタイムステップをプログラム作成者が決めます。そのタイムステップを$\Delta t$とすると、当然それ以下の時間刻みは見ることができないので、(B)のような仮定は数値計算では表現することができない(見ることができない)ことから想像できると思います。
(2)$\frac{\Delta \tau}{\Delta t}\gt 1$のとき
このような場合は、平衡状態(A)から別の平衡状態(C)へ向かう過程である(B)がはっきりとわかる流れとなります。
しかし、この場合もやはり、(B)を見たいかどうかに依ります。
もし見たいのであれば、その流れを表現するためには、流れを表現する流体力学や熱の伝わり方を表現する伝熱工学や、その他**非平衡の熱力学(統計力学)**などを用いる必要があります。
(2)のような状態を熱力学では考えることができないのです。
誤解をしないでほしいですが、
熱力学は確かに、流体や伝熱のような流れの状態を表現していませんが、だからと言って流体や伝熱で熱力学の状態変数温度や圧力が使えないという意味ではないです。
つまり、逆も成り立たないと思ってはいけないということです。
例えば、流体もマクロな流体粒子として温度や圧力を扱うのですが、それは熱力学での温度や圧力と同じであるかという議論もあるのですが、それが同じであるという立場で流体現象を扱っているはずです。
そういう意味で、流体は流れを解析するだけではなく、熱現象をも取り扱っているので**「熱流体」**という言い方もします。
感想:熱力学の成功
(2)のような詳細を表現できない熱力学がここまで発展するのはとても驚きであります。
個々の粒子の詳細な振る舞いに対しては、量子力学の力を借りなければなりませんが、それだけ膨大な数の粒子に対する連立方程式を解こうと思うと途方もない数になります。
それこそ、そんなのを解いているだけで人生が終わってしまいます(笑)
しかし、それだけ膨大な数の粒子がいるおかげで逆にそれらが相互作用と及ぼし合って平衡状態へと向かって行ってくれるおかげで、少数の変数だけで現象を理解することができるのは、すごい理論体系であると感じます。
補足
ところで、ちらっと**「それだけ膨大な数の粒子に対する連立方程式を解こうと思うと途方もない数になります。」**と触れましたが、本質的には相互作用しているおかげであるので、ここの粒子の振る舞いは、ある物理量(粒子の運動量(運動エネルギーや速度))は平均値まわりで分布を持ちながら統計的な振る舞いに従って運動しているということが後々わかるのですが、
相互作用がないなら、**理想気体はどうやって平衡状態に向かうのか?**ということが疑問になるかと思います。
※「理想気体」は分子間力を考えていないので・・・・
それに対しては、もちろん分子には相互作用が働いています。
しかし、その相互作用をいつも考える必要があるかどうかです。
理想気体の場合は、ある平湖状態から別の平衡状態へ向かうとき、その過程では分子間力があるので平衡状態に向かうと解釈し、一旦平衡状態になればその状態では分子間力を無視した理想状態と解釈してよいでしょう。