はじめに
こんにちは。takumikanです。
今回はbit全探索について個人的に学習したことをメモがてらまとめます。
問題や内容は逐次修正していきたいと思っています!!
目次
bit全探索とは
bit全探索とは、一言でいえば、全探索を行う実装の一つである。(そのまま)
といってもよくわからないので、具体例をみていきます。
例えば、以下のような問題を考えます。
10円,50円,100円を1枚ずつ用いて払える金額を求めよ。
このとき、単純な解法として、
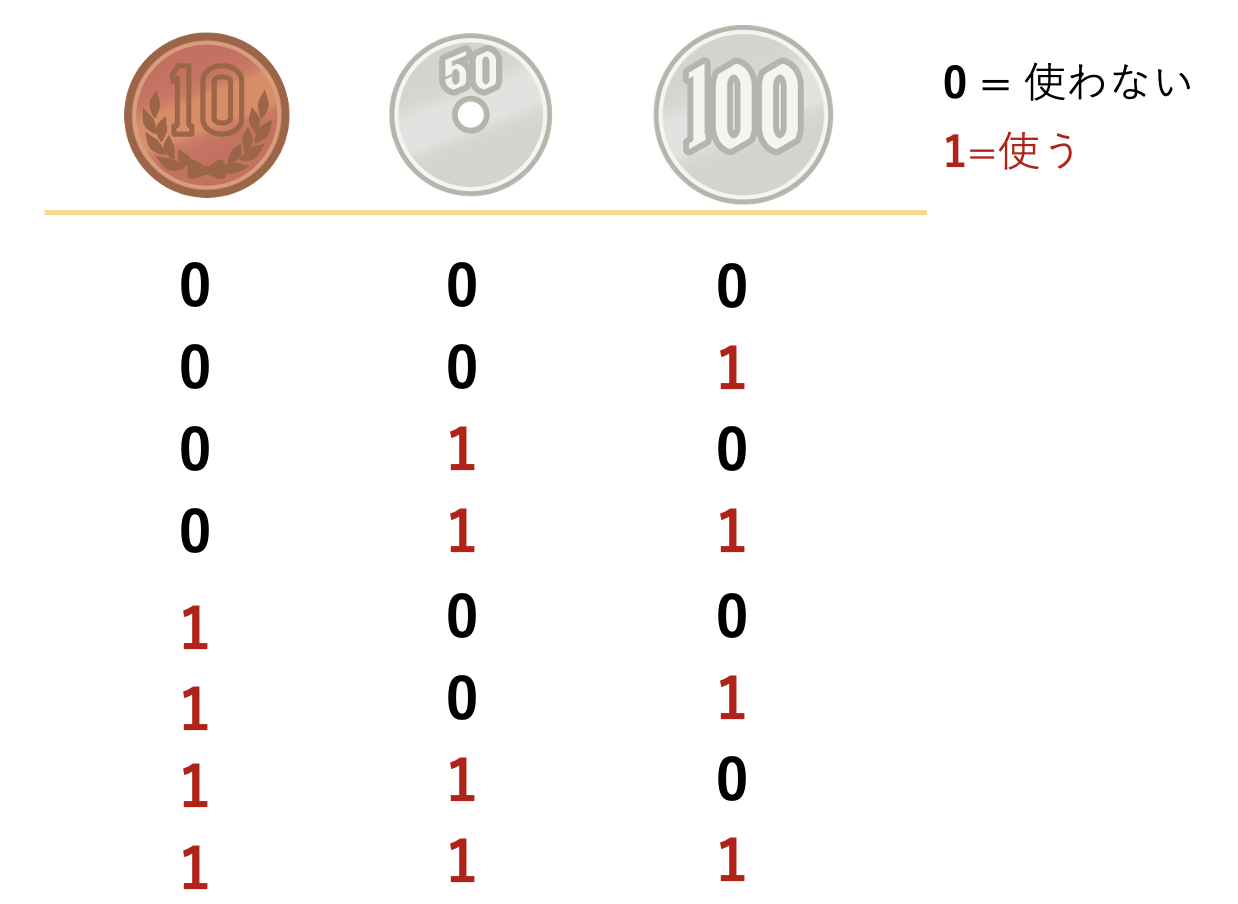
それぞれ「使う」「使わない」の2通りずつ、計$2^3 = 8$通り考えられる(以下の図参照)

一番上の行は、全て×なので、1枚も硬貨を使用しない = 0円
二番目の行は、100円のみ使用する = 100円
三番目の行は、50円と100円を使用数 = 50 + 100 = 150円
ということを表しています。
つまり、"10円,50円,100円を1枚ずつ用いて払える金額を求める"には、
"使うか使わないかの全組み合わせ(各行に対応)を求める"ことが出来れば良いことがわかります
(写真の全ての○×の組み合わせを求められればあとは1行ずつ金額を求めるだけ)
ちなみに、プログラム上では、"◯と×"は
"1と0"または"trueとfalse"で表します。
今回は0と1の組み合わせで求めることにします(下図参照)

それでは、この0と1の組み合わせをどのようにして求めれば良いのか。
この"0と1の全組み合わせ(各行)を求める"方法の一つがまさにbit全探索となります。
さらに
この0と1の列を眺めていると、2進数として見ることができますね(できない)
つまり、この各行を2進数と見れば、以下のようになります
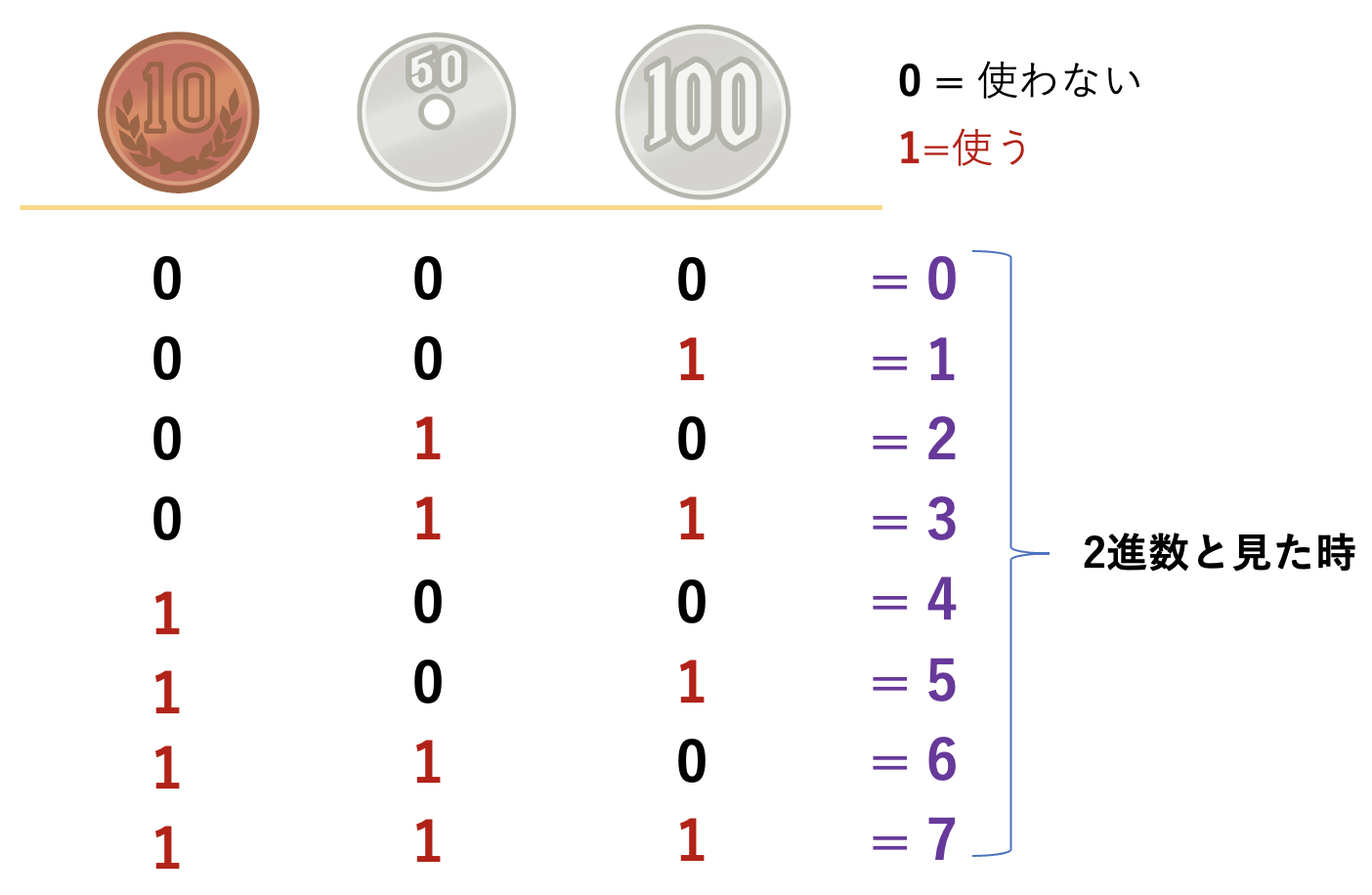
ここまでをまとめると、
- 要素がN個(この例では10,50,100円の3個)の場合は$2^{N}$の組み合わせがある。
- それぞれを使う使わないで0と1に分けると、各行が$0$ ~ $2^{N}-1$に対応する。
- 0が最初にあるため、$2^N$にならないことに注意(硬貨の例では最後は8ではなくて7)
実装
それでは、早速実装の方を見ていきましょう。
はじめに、実装の全体図を示します。
for (int bit=0; bit<(1<<N); bit++){
vector<int> use(N, 0);
for (int j=0; j<N; j++){
if (bit & (1<<j)) use[j]=1;
}
// useは[0, 0, 1]のような(各行のどれか)が作成できる
// useを使った何らかの処理
}
たったこれだけです。(笑)
※ Nは要素の数(最初の例では硬貨の数=3)を表しています
色々見慣れない(自分だけか)実装が出てきたので、1行ずつまとめます。
-
1<<Nについて
詳しく知りたい方は、"シフト演算"で調べてみてください。今回は簡単に紹介します
一言でまとめると、「1をN個だけ右にずらすこと」を表しています。
具体例の方がわかりやすいので、具体例を示します。
1<<0 : $1_{(2)}$ = 1
1<<1 : $10_{(2)}$ = 2
1<<2 : $100_{(2)}$ = 4
1<<3 : $1000_{(2)}$ = 8
1<<N : $100.....00_{(2)}$ = $2^{N}$
例えば、N=3の場合は1<<3=$100_{(2)}$$=8$を表します。(2進数で"=X"を求めていることに注意) -
1行目:
for (int bit=0; bit<(1<<N); bit++)
このfor文が示しているのは、bit$=0$ ~ $2^{N}-1$までのループ
すなわち、各行を2進数としてみたときの数字(紫の数字)を1つずつbitに代入しています。

-
2行目:
vector<int> use(N,0);
単純に、使うか使わないか(1か0か)を格納するvectorを作成しています。
つまり、各ループ(各行)ごとにuseを作成しています。
最初は全要素(硬貨の例では3要素)は0で初期化しています。
最終的な目標はこのuseの要素のうち使用する部分を1にすることになります
(下の画像の場合はuseの最後の要素を1に変更することになります)
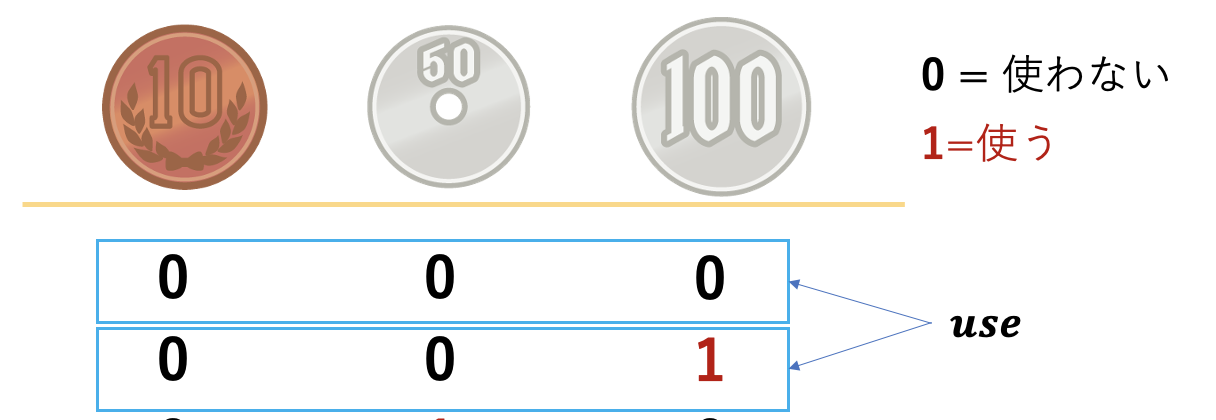
-
3行目:
for (int j=0; j<N; j++)
単純にjに0からN-1(=要素数-1)を代入しています。
硬貨の例では、N=3なので、0~2を代入します。 -
&について
シフト演算と同様に詳しく知りたい方は「ビット演算」で検索してみてください。
ここでは、X&YはXとYを2進数としてみて、andをとった結果を表す。と留めておきます
具体的には、以下の図に示します。

-
4行目:
if (bit & (1<<j)) use[j]=1;
確認です。useの目的はなんだったでしょうか。
useの最終的な目的は、1と0の組み合わせ(各行)の1の部分の要素を1にすることでした。
(例: 2行目の場合 [0,0,0] (初期化時) -> [0,0,1]にする)
つまり、結論から言うと、最後のこの部分で行っているのは、
初期化したuse=[0,0,0]のうち、使用する部分を1に変えることですそれでは具体的にみていきます。まずは2行目(以下)を例とします

bitが表しているのは、各行を2進数と見た時の数字(紫の数字)。つまり1でした。
従って、useの最後の要素を1に変換することが目標となりますjは3行目より0~Nの繰り返し、今回の例では0~2です。
つまり、1<<jは1を左に1ずつずらしていくことを表します。(1, 10, 100, ...)
従って、(bit & (1<<j))が表しているのは、
bitの各桁が1かどうかの確認を行っているだけです。
具体的に、j=0,1,2の時の挙動を以下に示します。
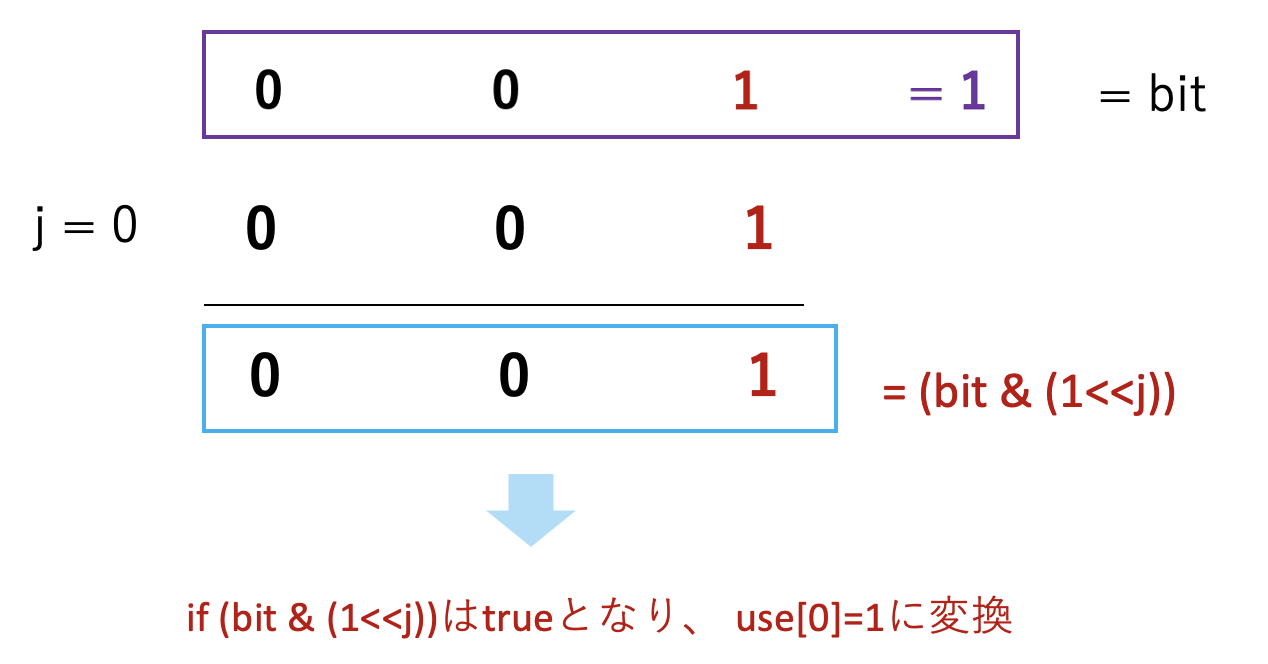
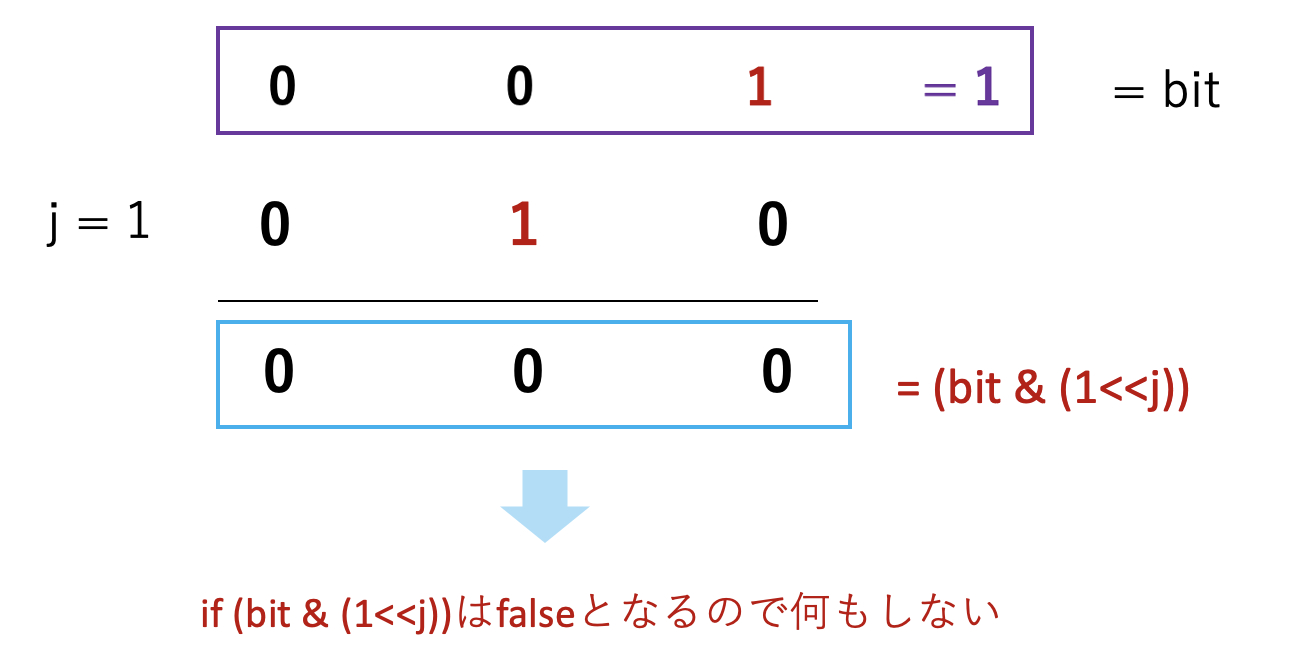

流れをまとめると以下のようになります。
- bit=0~$2^N-1$のそれぞれに対して、
j=0~N-1で1<<jとbitでand演算を行うことにより、bitの1の部分を取り出す - useが各ループごとに、各行に対応する1と0の組み合わせとなる。
従って、あとは、作成したuseに対して、何らかの処理を行うことによって、
当初の○と×の全組み合わせを調べることが可能になります。 - bit=0~$2^N-1$のそれぞれに対して、
再度硬貨の例の場合の実装コードを示しておきます。
// N = 3
// bit = 0, ..., 7
for (int bit=0; bit<(1<<N); bit++){
// use = [0, 0, 0]で初期化
vector<int> use(N,0);
// 使用する部分を1に変更
for (int j=0; j<N; j++){
if (bit & (1<<j)) use[j]=1;
}
// ここまででuseが作成される
// bit=0 : use=[0,0,0]
// bit=1 : use=[0,0,1]
// bit=2 : use=[0,1,0]
// ...
// bit=7 : use=[1,1,1]
}
例題
それではbit全探索を用いて実際に問題を解いてみようと思います。
今回はAtcoderの問題を利用させていただきたいと思います。
※ bit全探索の処理の流れをわかりやすくするため、全てをmain関数の中に書いたので、汚いのは悪しからず...(と思っていたけど1問目しかできてない。。)
※ マクロ等を極力使わずベタ書きするようにしましたが、使っていたらすみません。。
例題1(ABC167 C問題)
問題はこちらから
問題の要約
学びたいアルゴリズムがM個ある。N冊の参考書があり、i番目の参考書の値段は$C_i$円、各i番目の参考書を読むことで、j番目のアルゴリズムの能力が$A_{ij}$だけ向上する。全てのアルゴリズムの能力をX以上にすることは可能か。また、可能なら必要な金額の最小値を求めよ。
<方針>
Nは12以下なので、全探索を行っても計算量は問題なさそう。従って、全探索で求める。
この時、N冊の参考書をそれぞれ使うか使わないかをbit全探索で求めてみる。
#include <iostream>
#include <vector>
using namespace std;
constexpr long long INF = 1LL << 60;
int main(){
int N, M, X; cin >> N >> M >> X;
vector<int> C(N, 0);
vector<vector<int>> A(N, vector<int>(M, 0));
// input
for(int i=0; i<N; i++){
cin >> C[i];
for (int j=0; j<M; j++){
cin >> A[i][j];
}
}
// 最小値を求める問題なので、十分大きい値で初期化
long long ans = INF;
// bit全探索
for (int bit=0; bit<(1<<N); bit++){
vector<int> use(N, 0);
for (int j=0; j<N; j++){
if (bit & (1<<j)) use[j] = 1;
}
// 使用する参考書の全能力と金額の和を求める
vector<int> wa(M, 0);
long long price = 0;
for (int i=0; i<N; i++){
// 使用しない場合飛ばす
if (use[i] == 0) continue;
// 使用する場合
price += C[i];
for (int j=0; j<M; j++){
wa[j] += A[i][j];
}
}
// 全てがX以上か確認
bool flag = true;
for (int j=0; j<M; j++){
if (wa[j] < X) flag = false;
}
// 全てX以上ならpriceを比較して更新
if (flag) ans = min(price, ans);
}
// ansがINFのまま == X以上になるものがない
if (ans == INF) cout << -1 << endl;
else cout << ans << endl;
}
例題2(ABC147 C問題)
問題はこちらから
問題の要約
N人の人がいる。N人はそれぞれ、必ず正しいことを言う「正直者」または真偽不明のことを言う「不親切な人」のいずれかです。人iは$A_i$個の発言をします。人iのj個目の発言は$x_{ij}, y_{ij}$で表され、$y_{ij}=1$の時は人$x_{ij}$は正直者という証言であり、$y_{ij}=0$の時は人$x_{ij}$は不親切な人という証言である。このN人の中に正直者は最大何人いるか。
<方針>
Nは15以下なので、正直者(1)or不親切な人(0)で全探索を行えば良い。
この時、bit全探索を用いて求めてみる
#include <iostream>
#include <vector>
#include <map>
#include <algorithm>
#include <numeric>
using namespace std;
int N;
int solve(vector<map<int, int>> mp, vector<int> use){
// 正直者: 1 不親切: 0
for (int i=0; i<N; i++){
if (use[i] == 0) continue;
for (auto [xi, yi]: mp[i]){
if (yi==1 && use[xi] == 0) return 0;
if (yi==0 && use[xi] == 1) return 0;
}
}
return accumulate(use.begin(), use.end(), 0);
}
int main(){
cin >> N;
vector<map<int, int>> mp(N);
for (int i=0; i<N; i++){
int Ai; cin >> Ai;
for (int ai=0; ai<Ai; ai++){
int xi, yi;
cin >> xi >> yi;
mp[ai][xi] = yi;
}
}
int ans = 0;
for (int bit=0; bit<(1<<N); bit++){
vector<int> use(N,0); // 正直者
for (int j=0; j<N; j++){
if (bit & (1<<j)) use[j] = 1;
}
ans = max(ans, solve(mp, use));
}
cout << ans << endl;
}
参考文献
色々な本や動画を参考にしていますが、主に使用しているものを以下に載せておきます