これは「imtakalab Advent Calendar 2024」の22日目の記事です。
概要
著者は理系大学院の修士1年生で、主に機械学習について研究・学習しています。
先日「12 Days of OpenAI」にて、「o1」や「Sora」の正式リリース、新たなモデル「o3」が発表されました。その中でも「o1」は、強化学習における「chain-of-thought(思考の連鎖)」によって、これまでの言語モデルより遥かに高い性能を示しました。(下図)
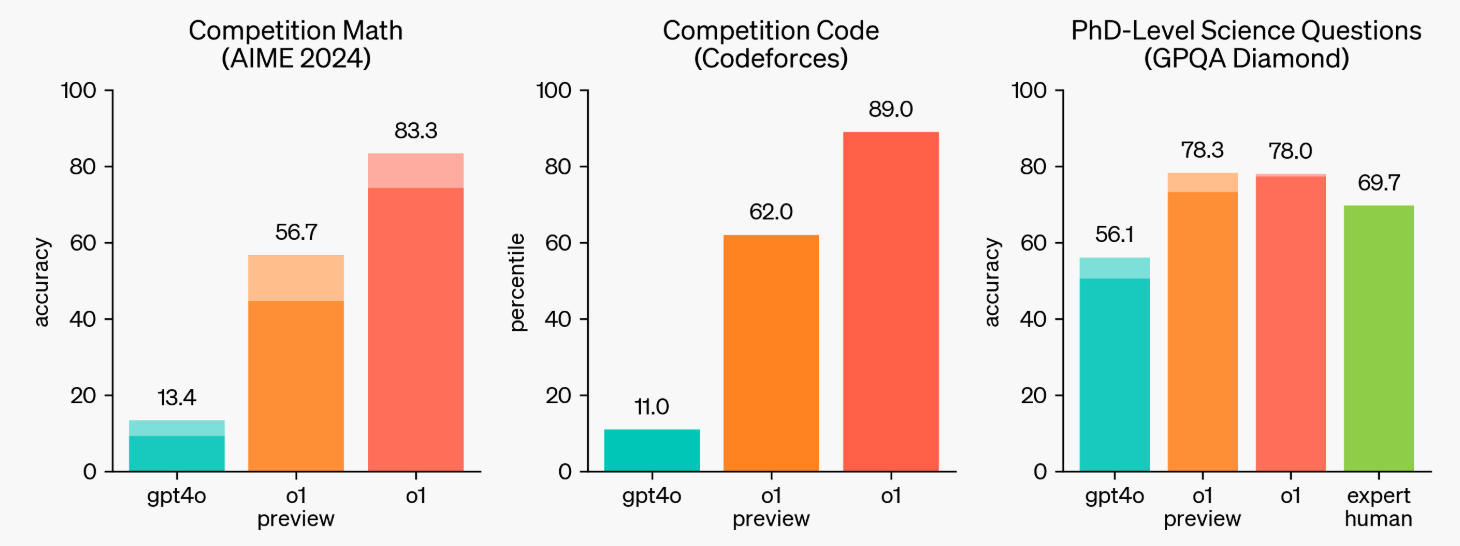
(https://openai.com/index/learning-to-reason-with-llms/ より参照)
この記事では、「o1」の「chain-of-thought(思考の連鎖)」の元になったと言われている以下の論文を紹介したいと思います。
STaR の背景
最近のLLM研究では、最終的な答えを出す前に、中間的な推論(rationales:根拠)を生成することが、性能を向上させることがわかっています。根拠を生成する方法としては以下の方法があります。
- 根拠を記したデータセットを構築し、ファインチューニングする
- 言語モデルのプロンプトに根拠の例を数個含める(few-shot Learning?)
しかし、それぞれの方法には以下の欠点があります。
根拠を記したデータセットを構築し、ファインチューニングする
→ データを作るのが大変
- 手作業でデータ作るにはコストが高い
- テンプレートを使用してデータ作成を自動化するには、一般的な説明がされている場合や合理的な理由が考えられる場合のみにしか適応できない
言語モデルのプロンプトに根拠の例を数個含める(few-shot Learning?)
→ 性能劣化
- 大規模なデータセットを使用して、答えを直接予測するようにファインチューニングさせたモデルと比べると性能は大幅に劣る手法です
以上の欠点を解決するために、この研究ではモデルが自ら根拠を生成し、その根拠に基づいてファインチューニングする手法 STaR (Self-Taught Reasoner:自己学習推論者)を提案しています。
提案モデルは学習済みのLLMをファインチューニングする手法であり、事前学習の工夫ではありません。
STaR の中身
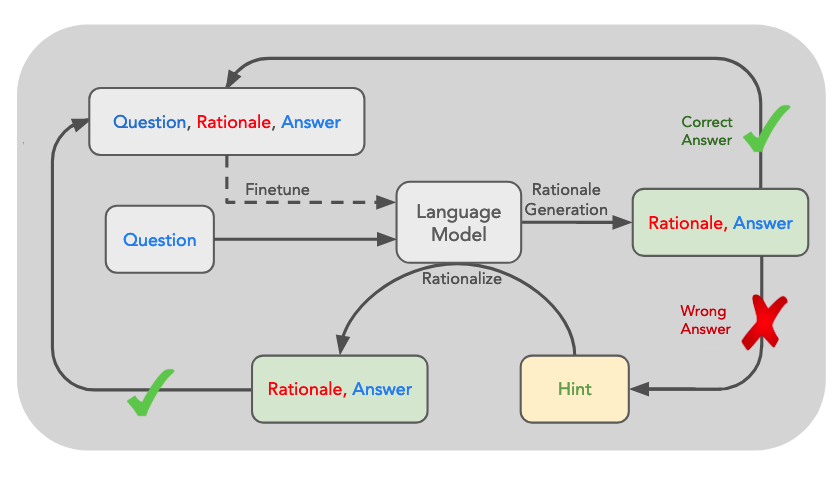
以下が概略図です。これからの説明はこの図と合わせた表記になっています。
中身は至ってシンプルで、Questionに対して言語モデル (Language Model) が、Answerと一緒にRationale(根拠)を生成します。
生成したAnswerが正しければそのRationale(根拠)で言語モデルをファインチューニングし、Answerが正しくなければ、Hintを与え、正しいAnswerとRationale(根拠)を得て、そのデータでファインチューニングします。(青字のQuestionとAnswerは与えられているものです)
アルゴリズムで書くと以下のようになります。難しい数式を使っているわけではないので、慣れている人はこっちの方がわかりやすいかもです。
STaR は、このような流れで、質問に対して根拠を推論するようになり、性能向上へとつながりました
具体的にどうやって学習するのか
ここからは、どのような目的関数を使って学習していくのかを記していきます。結論から言うと、STaR の目的関数は、強化学習における方策勾配法の目的関数の近似と見なすことができ、学習されます。
具体的には、モデル $M$ を離散潜在変数モデルと見なし、以下のように表現します。$x$ は質問文、$y$ は回答、$r$ は根拠を示します。
p_M(y|x) = \sum_r p(r|x)p(y|x,r)
つまり、モデル $M$ は質問 $x$ をされたら、潜在的な根拠 $r$ を元に、回答 $y$ を予測するということです。
このときデータセット $D={((x_i, y_i))}^{D}_{i=1}$ の全体の期待報酬は以下のように表されます。^は推定値を指し、$\mathbb{1}(\hat{y_i} = y_i)$は推定された回答 $\hat{y}$ が正解なら $1$ 間違っているなら $0$ を返す関数を指します。
J(M, X, Y) = \sum_i \mathbb{E}_{\hat{r_i}, \hat{y_i}\sim p_M (\cdot|x_i)} \mathbb{1}(\hat{y_i} = y_i)
ごちゃごちゃしていますが、こちらは正しく回答したデータ数を表しているだけなので比較的にわかりやすいと思います。要は、推定値 $\hat{y}$ が正解 $y$ となるデータを増やしたいので、この報酬期待値を最大化するように学習すればいいことになります。
この式が強化学習の方策勾配法の報酬期待値 $J(\theta)=\mathbb{E}_{\tau\sim \pi _\theta} G(\tau)$ の最大化と近似できるため、この方法で学習できます。
方策勾配法の$J(\theta)$がよくわからない人や、勾配計算でどういう式展開になるかわからない人は以下の ▶︎ で軽く解説しています
勾配計算の展開と補足解説
方策勾配法
方策勾配法とは強化学習手法の中でも勾配を使って方策 $\pi$ を更新する手法の総称で以下の目的関数で表されます。
J(\theta)=\mathbb{E}_{\tau\sim \pi _\theta} G(\tau)
ここで $\theta$ は学習されるパラメータ、$\tau$ は方策 $\pi$ の元で得られた試行錯誤の結果を表し、目的関数 $J(\theta)$ は試行錯誤 $\tau$ における報酬和 $G(\tau)$ の期待値を取っています。つまり報酬和を最大化するような $\pi$ となるように学習するということです。
この目的関数の勾配は以下のように表されます。(この計算過程は調べれば出てくると思います。研究室の学生はゼロつく4の付録Dに記載があります。)
\begin{align}
\partial_{\theta} J(\theta) &= \partial_{\theta} \mathbb{E}_{\tau\sim \pi _\theta} G(\tau) \\
&= \mathbb{E}_{\tau\sim \pi _\theta}\lbrack \sum_{t=0}^T G(\tau) \partial_{\theta} \log \pi_{\theta}(A_t|S_t) \rbrack
\end{align}
つまり、勾配の計算自体は、$\partial_{\theta} \log \pi_{\theta}(A_t|S_t)$でおこなわれ、その勾配を元にパラメータ $\theta$ を更新していくことになります。
STaR における勾配計算
STaR の目的関数 $J(M, X, Y)$ の勾配も、方策勾配法の導出過程と同様に求めることができます。
\partial J(M, X, Y) = \sum_i \mathbb{E}_{\hat{r_i}, \hat{y_i}\sim p_M (\cdot|x_i)} [ \mathbb{1}(\hat{y_i} = y_i) \cdot \partial \log p_M(\hat{y_i}, \hat{r_i} | x_i)]
結果
結果をちゃんと見たい人は、論文読むと思うので、ここでは軽くピックアップして紹介します。
結論:最終的な答えを予測するようにファインチューニングしたモデルと比較してパフォーマンスを大幅に向上させることができた。30倍大きい最先端の言語モデル(GPT-3)をファインチューニングした場合と同等のパフォーマンスを発揮した。
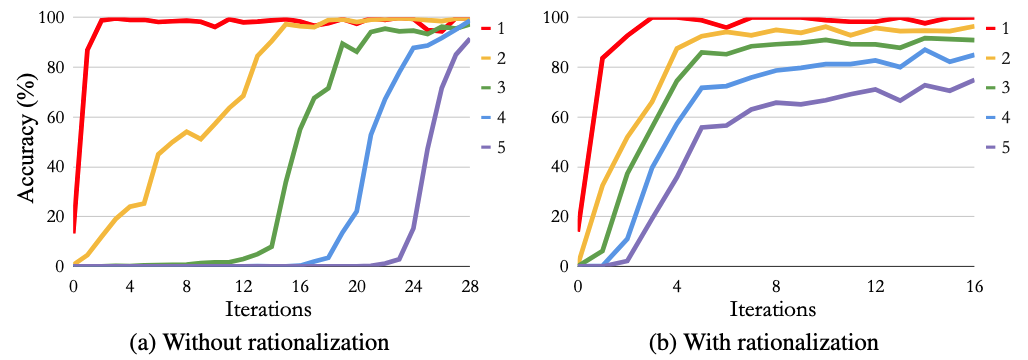
Arithmetic(足し算の計算)
n桁同士の足し算の計算ができるどうかの結果。1~5桁の結果で、根拠を生成した(b)のグラフの方が正解率が高い。
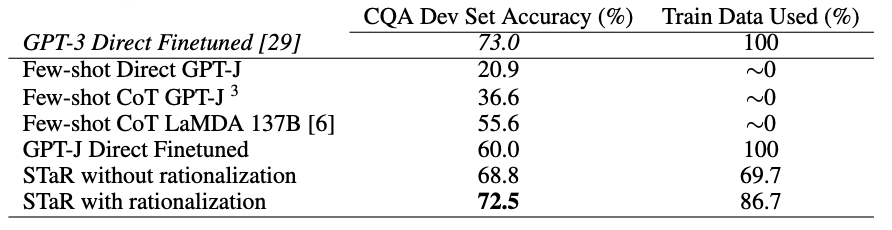
他の手法との比較
事前学習モデルGPT-J を元にしたファインチューニングだけでGPT-3と同等の性能を示した。
補足
課題として、初期モデルがある程度の推論能力を持つだけの大きさでなければいけない(根拠を推論できるだけのモデルでないといけない)制約や、変な推論をしてしまうこともあります。STaRを一般化した手法として、Quiet-STaRがあるので興味がある人は見てみてください。(今度survey勉強会で紹介するかもです)
おわりに
ここまで読んでいただきありがとうございました!!
LLMの「chain-of-thought」なんとなく掴めたら嬉しいです。
個人的には、方策勾配法の目的関数が出てきてテンション上がりました笑
ただ、LLMに関する事前知識ありきの記事だったので、わからなかった人は申し訳ないです!
途中、鎖系のネタを挟もうと思ってたのに、全然思いつかなかった...⛓️⛓️