「相関関係は因果関係を包含しない」
人口に膾炙した表現であり、統計を学んだことのあるものであればその実例(本屋と銀行であったり、教会と犯罪者であったり)もいくつか知っている者が多いと思う。
ではどのような場合に、相関関係が有意であるのにもかかわらず因果関係が存在しない場合にはどのような場合があるのか、整理して論じたい。
なお、本記事はタイトルのキャッチーさから有名な用語である「疑似相関」という用語を用いたが、「相関」レベルより深く「従属」レベルで同様の議論が成立する。着目している因子感が本来は独立であるにも関わらず従属であるという結果が得られる場合はにはどのような原因が存在するのかについて論じていくつもりである。
また、具体例の題材は分野を問わず様々採用しているが、筆者が生物系研究者である都合、生物系の例が多く登場する。
1. 偶然
データを統計的に扱う以上、偶然によって偽陽性が生じる可能性を排除することはできない。
例えば、相関係数を仮説検定することで相関の判定を有意水準を5%のもとで行うとすると、そもそも相関関係自体がなかったとしても5%の確率で有意であると判定されることになる。
回避方法
このリスクを下げるためには有意水準を引き下げるしかない。「有意水準を引き下げると有意差が出ない!でも偶然の可能性は減らしたい!」となった場合はサンプルサイズを増やして検出力を高めた上で有意水準を引き下げることになる。
2. 共通の原因を固定していない
おそらく最も有名な例であろう。着目している2つの因子に共通の原因が存在する場合に、仮に因子間に直接関係はなかったとしても相関関係が生じてしまう。Fig. 1のような場合に相当し、共通原因であるZの条件を揃えずにX, Yの相関を解析することが疑似相関の原因となるのである。「本屋が多い街は銀行も多い」などが該当する。ちなみにこのような場合、Zをtail to tailな因子であるという。Zの矢印が両方ともarrowtailを向けているためである。
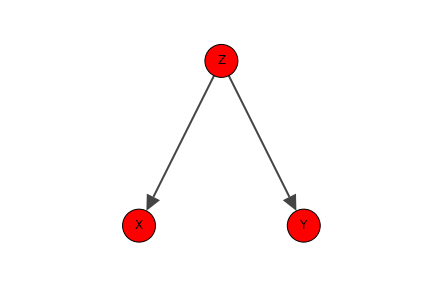
Fig.1 着目している2因子(X, Y)に共通の原因Zが存在する。Zはtail to tailである。
よくある共通の原因
人口、時代の違い、経済規模、年齢構成、科学技術水準、環境汚染度合い、年齢、、細胞数、細胞周期
回避方法
共通の原因となっている因子の条件を固定することによって解決できる。条件を固定する方法もいくつか存在している。
・原因の条件が同じになるように操作する、同等なもの同士で比較する。
条件を揃えて比較できるのであればそうするのが良い。問題点は共通原因因子を人為的にコントロールできず、値も対象ごとにバラバラである場合には適用できないことである。
・共通の原因の値で割って補正する
「人口あたり」や「GDPあたり」などの値同士で比較する。人口あたりの本屋数と人口あたりの銀行数の相関を見ることで人口の影響を排除するなど。しかしこの方法は着目している2因子が、共通原因因子に対してそれぞれ比例関係にあるときは上手くいくがそれ以外の場合は共通原因因子の影響が残ってしまったり、補正のための割り算が却って偽の相関性を生み出したりする恐れがある。
・偏相関を取る
ZでXとYをそれぞれ回帰分析を行ったのちに、その回帰残差どうしで相関をとることに相当する。Zで説明できなかった部分同士の相関となるのでZの影響を排除できる。線形回帰によってZの寄与を求めるために、共通原因因子のX, Yに対する作用が線形的にである場合に影響を除くことができることになる。割り算による補正との違いは切片を許容するか否かである。
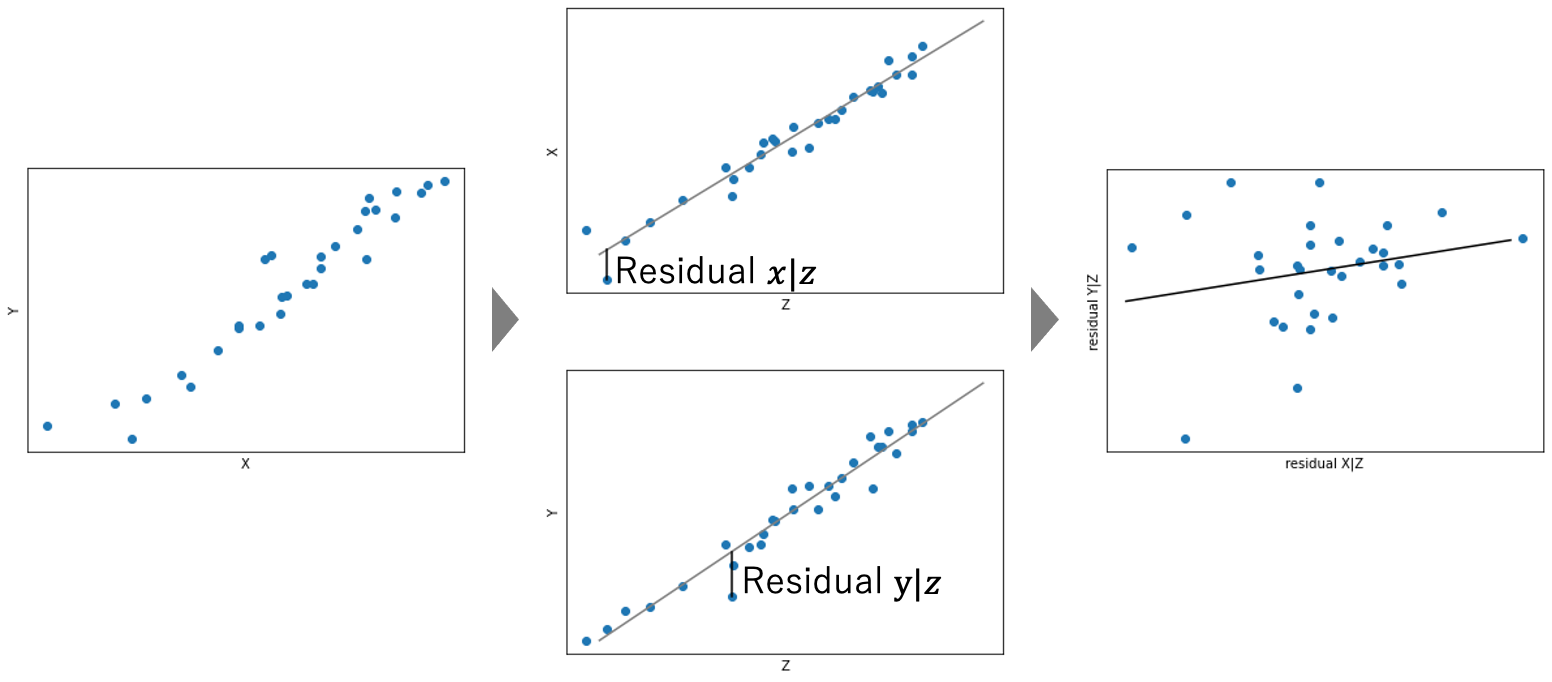
Fig.2 偏相関概念図。X, YについてそれぞれZで回帰して残差を求め、その残差どうしで相関を求める。X, Yが相関していそうなデータであったがZでの残差どうしはあまり相関していない。X, Y間の相関は主にZを介して作用しており、Zを固定すると関係は強くないことがわかる。
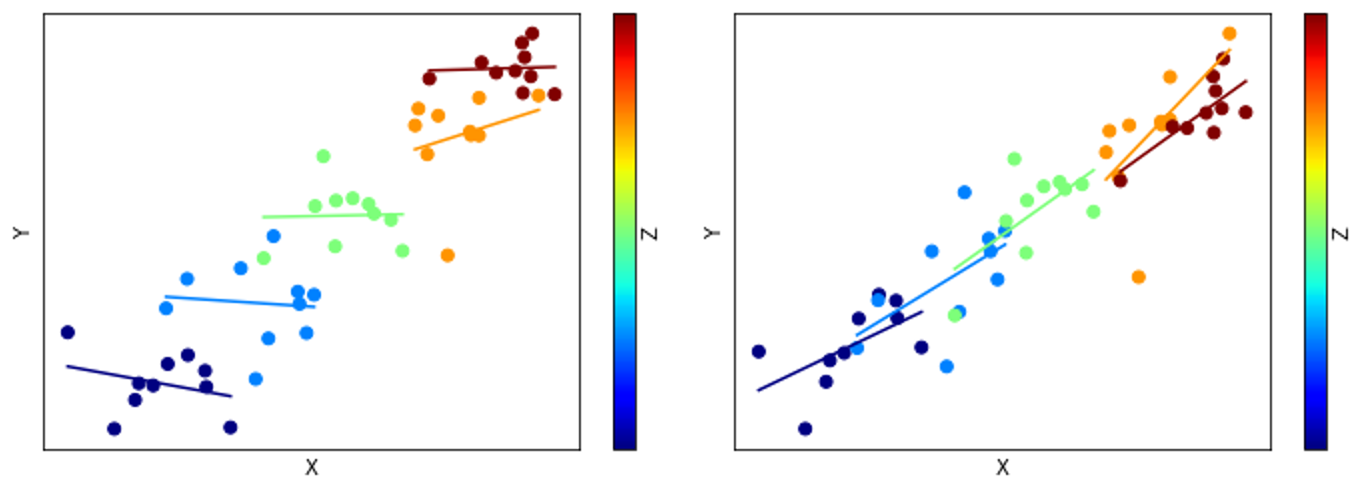
Fig.3 偏相関が低いデータと高いデータ。左: Zを固定したX,Y間の偏相関が低いデータ。X, Y全体として相関していてもZの値が同等のもので固定するとあまり相関しない。Zを介して作用していることがわかる。右:Zを固定したX,Y間の偏相関が高いデータ。Zの値が同等のもので固定してもその中で相関する。Zを介さずとも相関していることがわかる。
・条件付き確率を見る
X,Yが従属であるかどうかは$p(X)=p(X|Y)$が成り立つか否かなどで判定できる(相互情報量などを用いても等価である)。この際にZを固定した上でX, Yが独立かを判定したければ$p(X|Z)=p(X|Y,Z)$が成り立つかを検証すれば良い。
線形関係などを一切仮定せず一般的に成り立つが、確率分布を推定もしくは仮定する必要が生じてしまう。
特に$p(X|Y,Z)$を推定するには3次元データの分布を推定する必要があり、確率モデル(正規分布など)を仮定しない場合はサンプルサイズが大きくないと推定誤差が問題になる可能性がある。
*共通原因の特殊な例:2つの時系列データの相関
Fig.4 のように2つの時系列データを用いて相関解析を行うと、疑似相関が生じる危険性が極めて高い。これは「時代の変化、時間の経過」というものが共通の原因となってしまうからである。その理由として「同時並行」と「時間蓄積」の2つの要因が挙げられる。
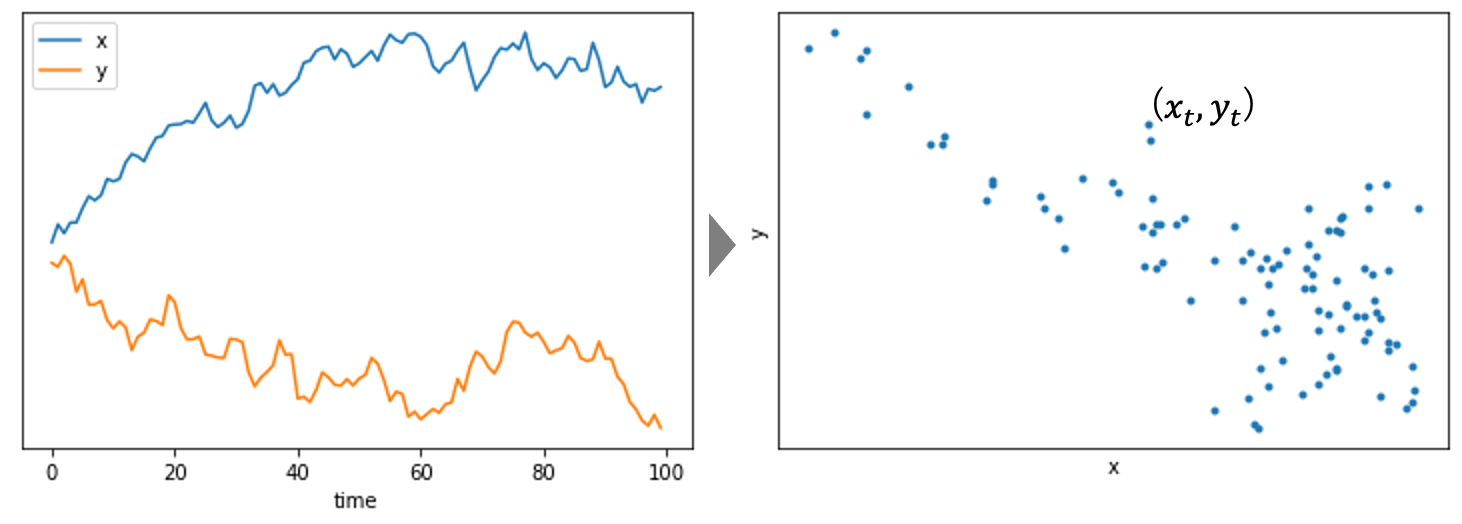
Fig.4 時系列データの相関解析の概念図
同じ時間の変化の中で様々なことが同時並行に起こるため
1つの時間軸の中で様々な同時に起きているために、ある出来事の進行が、別のある出来事の進行の時期と一致しているからといってそこから何かを論じることは難しい。
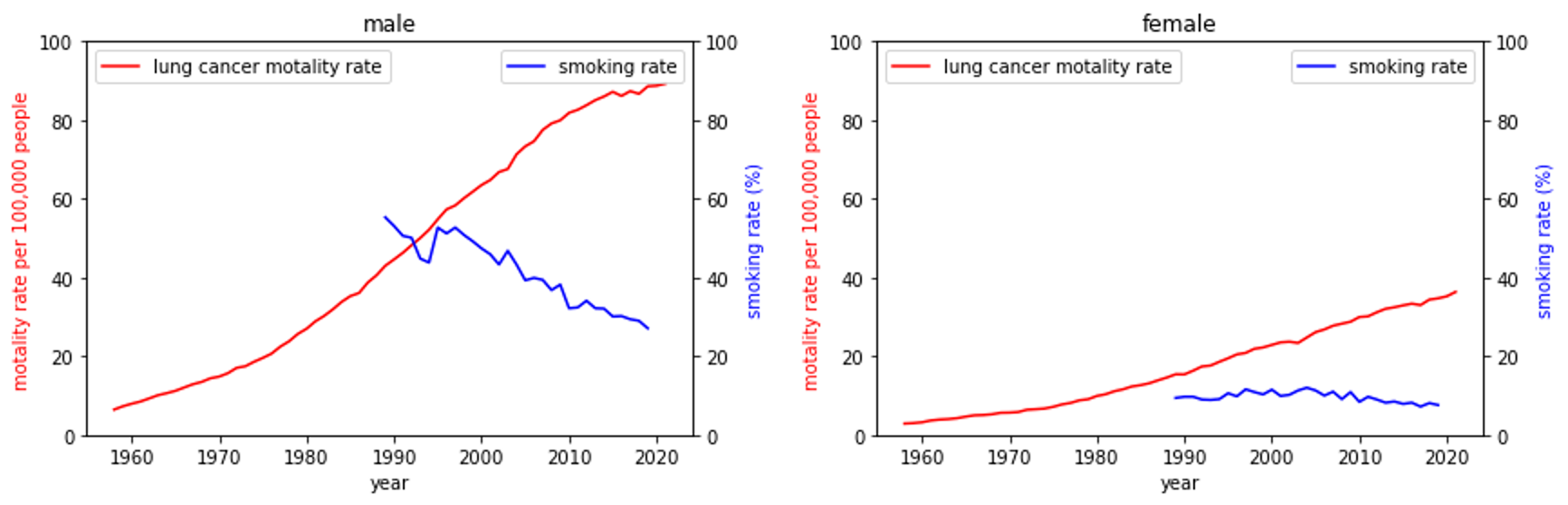
有名な例として「喫煙率が下がると肺がん死亡者率が上昇する」というものがある。
Fig.5 喫煙率と肺がん死亡率の推移。
特に男性で喫煙率が減少し続けている一方で、肺がん死亡率は増加し続けているのがわかる。(女性は喫煙率はほぼ横ばいだが、2000年手前まで増加したのち2010年手前頃から減少に転じている)
しかし多くの調査で喫煙は肺がんリスクを高めることは繰り返し示されている。この一見矛盾したデータを解釈する鍵は「高齢化の進行」にある。
時代の進行と伴に高齢者比率が高くなるために過去と現在で肺がん死亡者率をそのまま比較すると、過去のデータについては「若者が比較的多い集団の肺がん死亡者比率」、現在のデータについては「年寄りが比較的多い集団の肺がん死亡者比率」を比較していることになる。
肺がんリスクは加齢ともに増加するため単純に高齢者比率が高い現在のほうが肺がん死亡者率が高いという結果となってしまう。
これを回避する方法は簡単で、年齢の条件を揃えば良い。方法は2つあって、「同じ年齢帯同士で肺がん死亡者率を比較する」か「集団の年齢比率を年齢構成がおなじになるように補正する」のいずれかになる。
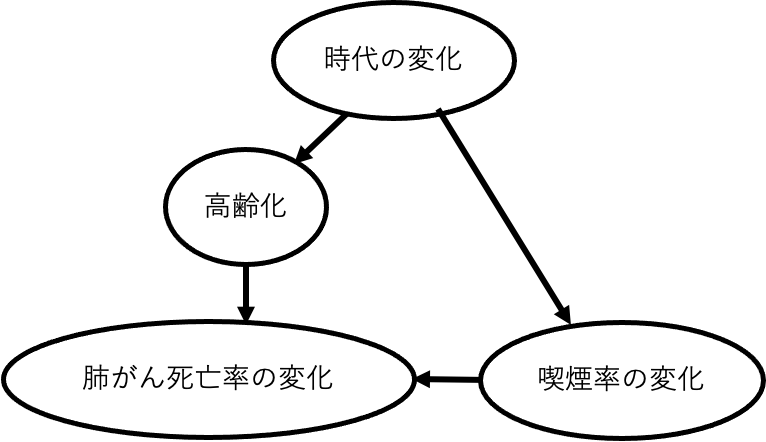
Fig.6 時代の変化が喫煙率の減少と高齢化の進行を同時に引き起こしている。時代を固定して解析できればそれで良いが、時代変化で肺がん死亡率増加が生じた要因として高齢化を考えれば、年齢を固定することで喫煙率と肺がん死亡率の関係を解析できるはずである。
同じ年齢帯同士での推移を見たのがFig.7 である。男性データについて喫煙率の低下の後、タイムラグがあるものの同じ年齢帯内であれば肺がん死亡率は低下していることがわかる。男性データで肺がん死亡率減少に転じるまでにタイムラグがあったことを考えると、女性データについては、まだ喫煙率が減少に転じて10年ちょっとしか経っていないうえ、そもそも喫煙率が男性ほど高くないため今後減少に転じる可能性はあるが男性ほどの劇的な変化はしないかもしれない。
Fig.7 年齢帯ごとの喫煙率と肺がん死亡率の推移。同じ年齢帯内で比較すると男性の肺がん死亡率は減少に転じていることがわかる。
年齢構成を補正するというのは、集団全体における死亡数は各年齢帯における死亡率と人口比率を用いて
$\sum$(各年齢帯における死亡率)(各年齢帯の人口比率)
と表現できるが、各年齢帯の人口比率を(各年のものではなく)基準年のものに統一して使用することで、年齢構成が基準年のもので一定であったと仮定した場合において死亡率がどのように推移するのかを検証できる。年齢構成変化によるものではなく、年齢帯ごとの死亡率変化がどのように影響するのかを確認するために使用され、疫学分野では年齢調整死亡率などと呼ばれる。Fig.8 が(1990年を基準年にした)年齢調整死亡率の推移を示した結果であり、年齢構成の変化を無視すれば肺がん死亡率も減少に転じているがわかる。
当然ではあるが喫煙による肺がんリスクは、コホート解析(喫煙していた人とそうでない人を追跡調査して肺がん発症率や死亡率に差が出るかを調べる)などのより詳細な調査で確かめられており(Sobue et al.)、今回示したような社会全体の喫煙率と肺がん死亡率推移を比較するような大雑把な解析のみで示されていることではない。
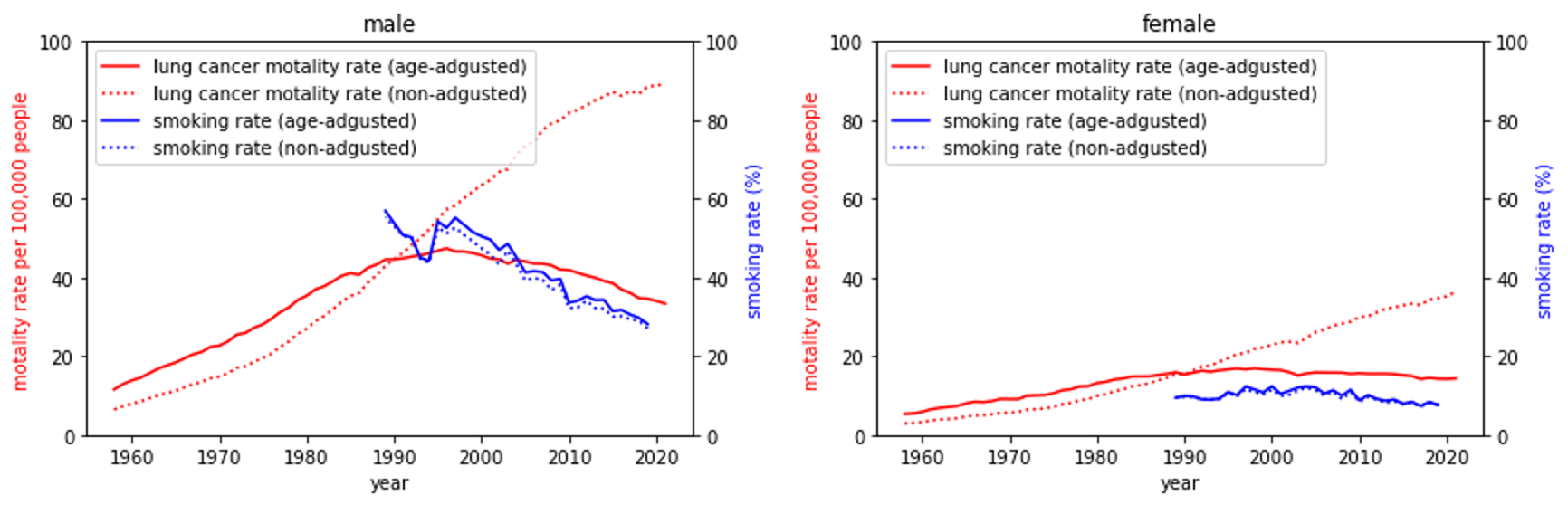
Fig.8 喫煙率と年齢調整肺がん死亡率の推移。実線は年齢調整あり、点線は年齢調整なし。年齢調整は1990年を基準に行った。
より一般的には、年齢調整のように構成割合を一定に揃えた上での加重平均比較法をラスパイレス方式といい、こうして計算される値をラスパイレス指数という。物価比較(消費性向が一定だと考えたときの生活物価の変化。)であったり、人件費比較(職位・階位構成が同じだと仮定したときの平均人件費。同じ役職なら同程度の報酬となっているかを検討する。)などに用いられることが多く、特に国家公務員と地方公務員の人件費比較などでよく用いられる。
時系列データにおいて
社会全体規模:人口の増加、経済成長、グローバリズムの進行、高齢化の進行、科学技術の発展、環境汚染の進行、教育の普及(識字率の上昇、大学進学率の増加)、IT化の進行など
集団規模:構成メンバーの増加、構成メンバーの高齢化・世代交代、社会的認知度や影響度の変化、売上や株価の変化、
個人規模:身体の成長と老化、社会経験の蓄積、社会的地位の確立など
もちろん、もっと大きな規模では天文学的規模や地質学的規模、進化論的規模、小さな規模では細胞規模(細胞周期や増殖、分化の進行など)などいくらでも存在する。
例としてはいくらでも考えられるが、以下のものを挙げておく。
・高齢化が進むと年平均気温が上昇する?
-> 先進国で高齢化が進行した時代と地球温暖化が進行した時代が概ね一致している。
・身長が高いほど数学的思考力が高い?
-> 異なる年齢の子供がごちゃまぜの集団に対する調査結果であれば、年齢が高い子ほど背が高くなり、より高度な数学にも慣れている傾向にある。
「時間的な蓄積の結果である」ということ自体が共通原因となっている
時系列データというものはその多くが「現在の値は、過去の蓄積の結果」となっている。
例えば体重は日々増減するが前日に細身だった人は次の日も細身である可能性が高い。それは「前日からの増分」は日々独立に変動していると仮定できるような場合であったとしても、その蓄積結果である「現在の体重」は容易にリセットしないためである。昨日までの自分はなかったことにはならない。
このために、時系列データ同士を比較した場合両方ともに「時間的な蓄積」という要因が共通の原因として乗ってくることになり疑似相関の原因となりうる。 実際、ランダムウォーク(長さ50)で独立に生成した人口時系列データどうしで回帰分析を行うというのを100回繰り返したところ、互いに独立過程であるに関わらず100回中76回で有意水準5%で有意であるという結果が得られている(Granger and Newbold)。ちなみに単回帰分析で回帰係数(傾き)が有意であるかという検定と、相関係数が0であるかという検定は数学的に等価であり、この結果は独立なランダムウォークどうしが無相関ではないではないということを意味している。
ランダムウォークは、各ステップに定常、独立な乱数が生じ、その累積和として現在の値が決まる過程である(単位根過程という)。つまり、「独立なランダムウォーク」というのはあくまで「各ステップで増加するか、減少するか」というのが試行ごとに独立なのであって、「現在の値がこれまで変化の蓄積である」という点で共通してしまう。したがって、独立なランダムウォークであるかを検討したければ各ステップの差分列(階差数列)どうしを比較するなどを行う必要がある。
ランダムウォークであると仮定できるのであれば階差をとることで解決できるが、世の中の(人間が注目したいと思うような)時系列データの多くは「時間的な蓄積の結果」ではあるが、「定常、独立な変化の蓄積」とまで言えるかは怪しい(対象データごとに性質が異なるし、研究分野ごとに傾向は異なるだろう)。万能の解析手法は存在しないが、複雑な事象になると非定常過程を含む数理モデルを構築し、X, Y間の作用を意味するパラメータの感度を解析したり、X, Y間作用がないと仮定したモデルと比較したりして根拠を固めていくなどが必要になるかもしれない。
相関解析を行う標本は同一時系列から抽出するのではなく反復実験を行う、もしくはX, Yのうち原因と思われる方(ここではXが原因とする)に対して実験的に介入できるならXを変化させXが「過去の変化の累積値」でないように制御する(実験的はXへの介入強度の順番を無作為化させ、反復的に変化させるなどを行い、Xの設定値とYのピークやAUC、終端値などの相関を見る)などが対処として考えられるが、研究分野や材料などによってはこのような対処は不可能であることも多い。だからこそ、時系列解析手法は実験的介入や反復計測に限界のある社会科学や金融工学などの分野で応用が発展しているといえる。
逆は真ならず
以上のように共通の原因を固定すれば、その影響を排除した上での相関性を解析することができる。つまり、「Zが共通の原因である」ならば、「Zを固定することで(X, YにZを介さない作用がないなら)X, Yの相関はなくなる」は正しい。
しかしながら、「X,Y間に相関があったが、因子Zを固定するとX, Y間の相関がなくなった」からといって、「Zは共通の原因であるということはできない」。Fig.9のようにZがX, Y間を媒介する因子である場合でも同様の結果が得られることになる。このようなZはhead to tailであるという。
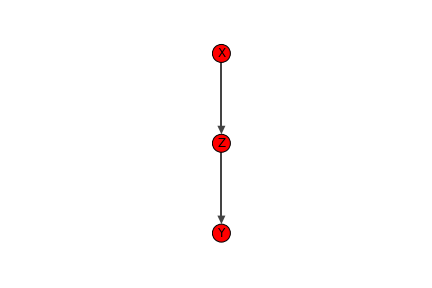
Fig.9 着目している2因子(X, Y)間を媒介するZが存在する。Zはhead to tailである。
このような場合にX, Y間に因果関係があるというか否かは少々哲学の問題になる。「直接的な結びつきがなければ因果関係があるとはいえない」と言った立場もありそのような立場で論じると、この場合は因果関係がないことになる。したがって、「因子Zを固定するとX, Y間が独立であるならばX, Y間に因果関係はない」といえる。しかしながら、この立場は突き詰めると量子力学、素粒子物理学などのレベルまで分解しないと因果関係が存在しないことになり実用上無意味になる。日常的に遭遇するすべての事柄はよりミクロな事象を媒介して生じているからである。
よって一般的には媒介する因子が存在していても原因と結果の鎖でつながっているならば因果関係があるとみなすことも多いと思う。こちらの立場であるならば「固定することで独立になったからと言って因果関係がないと言えない」。
3. 共通の結果を固定している
共通の原因を固定しなければ疑似相関が生じることを論じてきたが、逆に「共通の"結果"を"固定する"ことで」疑似相関性が生まれてしまう場合がある。Fig.10 でいうところのZはX,Yの共通の結果となっているが、このときにZを固定してしまうとX, Y間に相関などの従属性がもたらされることになる。このときのZはhead to headであるという。
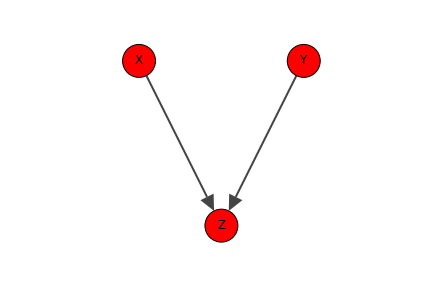
Fig.10 着目している2因子(X, Y)に共通の結果Zが存在する。Zはhead to headである。
初学者を混乱させやすいのはこの場合であり、後述するように有名なモンティ・ホール問題もカテゴリに属する。
まずはモンティ・ホール問題よりも簡単で理解しやすい例題から入ろう。
美大生問題
この問題は実データによるものではなく仮想的なものである。別に美大でも芸大でも音大でもなんでもよい。
美術の才能と勉学の成績に相関があるのかを検証するために美大生を対象に、実技の成績と学科の成績を調査したところ負の相関があることがわかった。このことをもって「勉強が苦手な人ほど美術の才能に恵まれている可能性が高い」などと論じることは可能か。ただし、その美大の入試は実技と学科の合計点によって決まっているとする。
このような問題を出している段階で、答えは「論じることはできない」に決まっているのだが、なぜその様になるかわかるのだろうか。
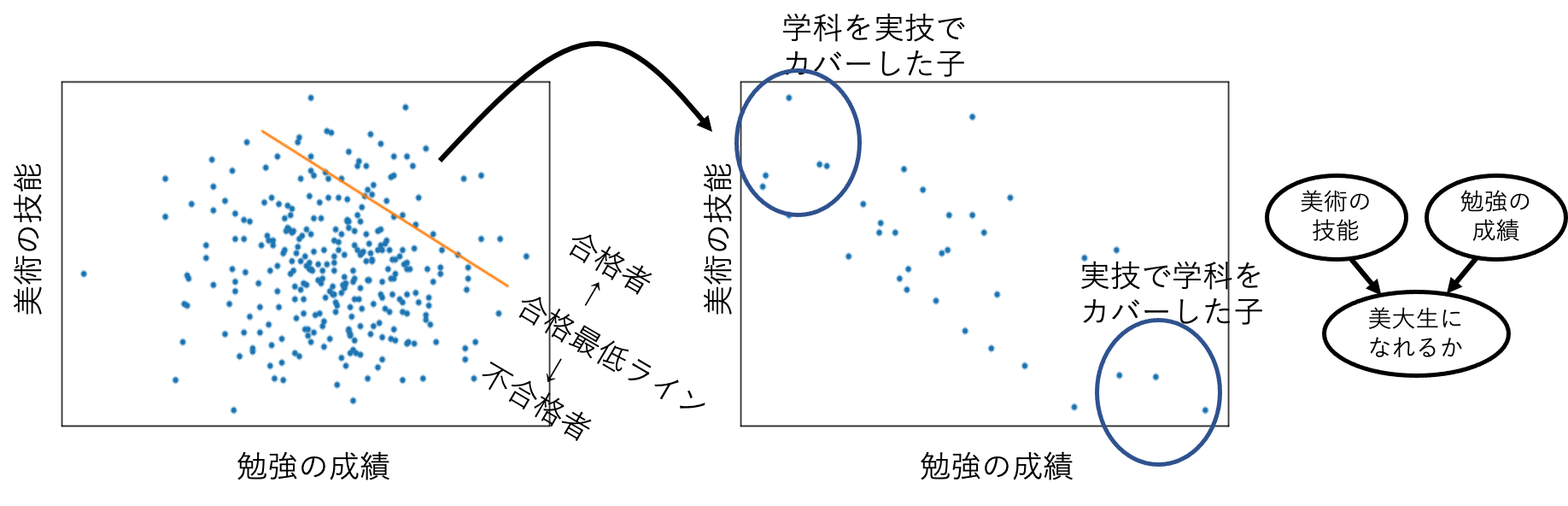
理由は調査対象者を美大生に限定したことに由来する。もし仮に世間一般で勉強と美術の実力に何の関連もないと仮定したとしても、実技・学科合計点が合格最低点以上のものが美大生になれることを考えると、Fig.11 のように斜めに切った境界線で調査対象者を選定していることになってしまう。
Fig.11 美大生問題概要。調査対象者を美大生に固定したことで、偽物の相関が生み出されている。美大生になれるかは美術の技能と勉強の成績の共通の結果であり、調査対象者設定によって母集団から斜めに集団を切り出してしまっている。美術の技能に特に秀でた子だけが勉強が他の受験生より苦手でも合格でき、また勉強に秀でた子だけが少し実技で失敗しても合格できるため負の相関を示しているが、これは対象者選定方法によって生じた相関である。
したがって、負の相関はもともとの集団に内在していたものではなく、調査対象者の選定方法によって生じたものである可能性が発生してしまう。実技の成績が良かったおかげで苦手な勉強がカバーできた子や勉強が得意だったおかげで実技が多少奮わなくても合格できた子というのが現れる(両方悪いと不合格である)ために負の相関が生じているのであって、元の集団の性質そのものではない。
合格者を垂直もしくは水辺な線で切っていれば(元の集団の一部分だけかもしれないが)切り方によって相関が生じることはない。これは実技のみ、あるいは学科のみで入試を行った場合である。問題は斜めの境界線で切り出した場合である。
調査対象者の選定など条件の固定を、着目している因子の「共通の結果」となっている場合に斜めの境界線が生じることになる。
兄弟のプリン問題
2人兄弟の子供のためにプリンを2つ買ってきて冷蔵庫に入れておき1人1つ食べて良いと書き置いたとする。少し経って冷蔵庫を見ると残り1つになっていた。兄に尋ねるともうプリンは食べたと答えた。弟はプリンを食べただろうか。
答えは非常に簡単であり、まだ食べていない。しかしながら、兄と弟が独立にプリンを食べると仮定すると兄が食べたかを尋ねても本来は弟がプリンを食べたかはわからないはずである。なぜ本問ではそれがわかるのか。
それは残りのプリンの数を観測していることに由来する。「残りの数」は「兄がプリンを食べたか」と「弟はプリンを食べたか」の共通の結果である。したがって「残りのプリンの数」と「兄がプリンを食べたか」を観察することで逆算して「弟がプリンを食べたか」を推測できるようになっている。
兄弟のプリン問題は美大生問題よりも遥かに単純で答えは簡単に当てられる。しかし、重要なポイントは実は共通であり共通の結果の固定による斜めの境界線の設定なのである。
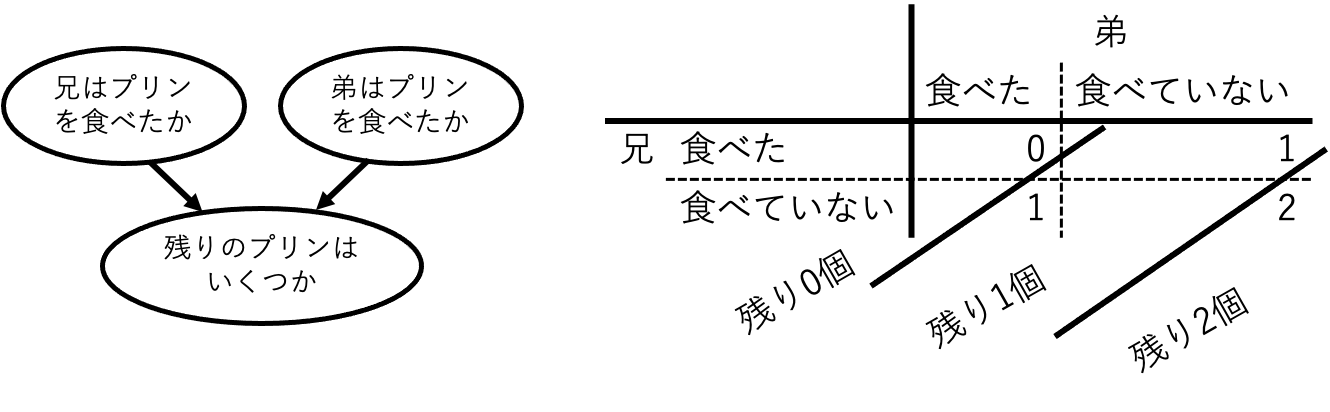
Fig.12 兄弟のプリン問題。残りのプリンの数は「兄がプリンを食べたか」と「弟はプリンを食べたか」の共通の結果であり、観察することで斜めの境界線を引くことになる。
モンティ・ホール問題
モンティ・ホール問題は有名な問題であるので、この場で説明しなくても知らなければ検索してくれという気もするが一応、解説しておく。クイズ番組において3つの扉から1つの扉を選択するという、問題が課される。正解の扉が1つありそれを開くと車が停めてあり、その車がプレゼントされる。残り2つの、不正解の扉を選ぶとやぎがいる(やぎ自体は別にどうでも良い)。
まず挑戦者が1つの扉を選ぶ。すると、その扉を実際に開く前に、司会者が残る2つの扉から1つを開いて見せる。中身はやぎである。そのうえで挑戦者には最初に選んだ扉をそのまま開くか最後の1つの扉に変更するか選ぶことができる。変更するのとそのまま開くのどちらが有利かという、問題である。
この問題はあまりに有名なので、なぜそのような結末になるのか全く理解できない方でも、答えは「変更したほうが有利である」なんなら「変更した場合2/3, そのままなら1/3で当たり」であるということまでご存知の方も多いのではないだろうか。その理屈を解説する。
この問題の肝は「司会者が2つの扉から無作為に開いておらず、やぎの扉を選んで開いている」という(問題文には書いていない)クイズ番組のお約束である。もともと挑戦者が車の扉を選んでいたら、残る2つの扉(どちらもやぎ)からランダムで開く。一方で、もともとやぎの扉を選んでいたら、(車の扉の方ではなく)やぎの扉の方を選んで司会者は開ける。司会者が車の扉を開けてしまって、挑戦者に変更するかどうか聞く前に企画終了!なんてどっちらけの展開にはならない。Erdösなどの数学者がモンティ・ホール問題を間違えたことは有名であるが、それはこの暗黙のお約束を考慮に入れて解いていなかったことに由来する。
こう考えれば「変更したあとに車の扉になる確率は、最初の選択の時点でやぎを引いていた確率(=2/3)に等しい」ことが容易にわかるし、「変更せずに車の扉を選ぶ確率は、最初から車の扉を選んでいた確率(=1/3)に等しい」ことも当然だと思う。「最初にやぎを選んでいて、かつ司会者が車の扉を開けてしまう」という事態がないためである。「開いた先にやぎがいる」ことに情報があるのではなく(それは開く前からわかっている)、残る扉から「やぎの扉はどれであるか」を教えてくれているのである。
変な話に感じるかもしれないが同じように「司会者が開けた扉がやぎだった」という結果を観察したとしても、「司会者はやぎの方を選んで開けた」と考えるか「無作為に開けた結果、たまたまやぎだった」と考えるかで変更することに意味があるかどうかが変わるのである。
これも実は共通の結果を観察することによって従属性が生じることとして説明が可能である。本来は「挑戦者がどの扉を選ぶか」と「どれが車の扉であるか」は独立である。「挑戦者が最初に選んだか」で正解の扉であるか否かの確率が変わることはありえない。しかしながら司会者は「挑戦者が選んでいない扉であってかつ、やぎの扉」を選んで開いている。したがって「司会者がどの扉を開くか」を観察することで「挑戦者が最初に選んだ扉はどれか」と「どれが車の扉であるか」が従属の関係となってしまい確率が変わるのである。これは扉選択問題にもともと内在していた性質ではなく、共通の結果(司会者の開いた扉がどれか)を観察したことの帰結である。
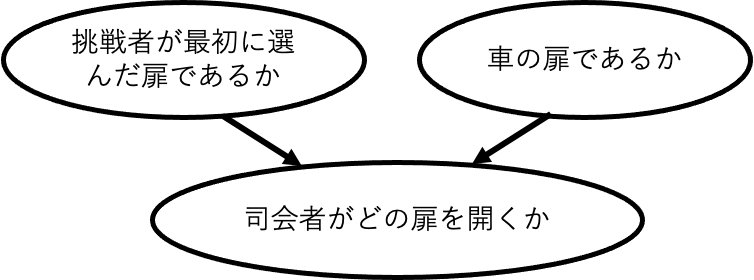
Fig.13 モンティ・ホール問題。司会者は「挑戦者が選んでいない扉であってかつ、やぎの扉」を選んで開けているならこの図の通り、司会者が開く扉は「挑戦者がどの扉を選ぶか」と「どれが車の扉であるか」の共通の結果になる。
もし、司会者がやぎの扉を選ばずに、残る2つの扉から無作為に開けているとFig. のようになる。この場合だと司会者がどの扉を開けたかは共通の結果にならない(車の扉であるかに依存しない)ために、司会者が開いた扉がやぎの扉でも、変更することは何の意味も持たないのである。
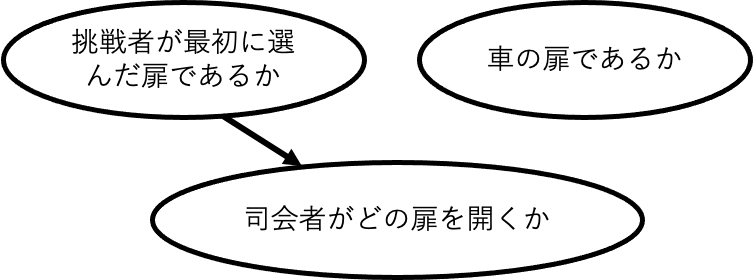
Fig.14 司会者が無作為に開けていると仮定した場合。司会者の開ける扉は共通の結果ではないので観察しても、それによって「挑戦者がどの扉を選ぶか」と「どれが車の扉であるか」の間に従属性が生じることはない。
最後に
偽物の相関に悩まされたくなければ、共通の"原因"であるならば固定する必要がある一方で共通の"結果"は固定してはならない。このことは概念的には理解できるが実務上の問題を生み出してしまう。多くの場合、何が原因であり何が結果であるかなど容易にはわからないからである。Grenger因果性検定やtransfer entropyなどの因果推定法(ある値が別のある値の先行指標となるかを判定する)を使用して解決できる場合もあるかもしれないが、検証したい因子とともに条件付を行う因子も時系列データとして取得できること、それらが非循環変動をしていること、定量的に測定したり客観的に判定することができることなどが要件となってくる。
たとえば、細胞生物学的な実験(ライブセルイメージングなど)を行って複数のシグナル因子の活性を解析したとする。その際、観察対象の細胞を選定するにあたって「元気の良さそうな細胞」を選んでいたりする。これは再現性などの観点から「死にかけなどの怪しい状態の細胞は使わない」という配慮から行っており多くの場合妥当である(と現在のところみなされている)。
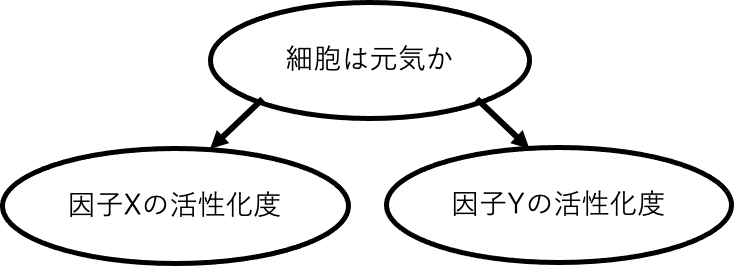
Fig.15 「細胞が元気か」がシグナル因子X, Yの正常な応答性の原因となっている場合。元気な細胞を選ぶことで、細胞が元気か否かの違いによって生じる偽物の従属性(元気な細胞はどちらの応答も強いなど)を排除して、X,Y間に制御関係がありそうかなどの解析を行うことができる。
「元気が良い状態か否かでシグナル応答性が変わる」となっているなら(複数のシグナル因子活性の)共通の原因であるために固定するのが正しい。一方で「各シグナル因子の発現量によって細胞が元気かどうかが変わる」という条件なら細胞が元気そうであるという条件付けによってシグナル間の従属性が生じてしまう場合があるを意味している。
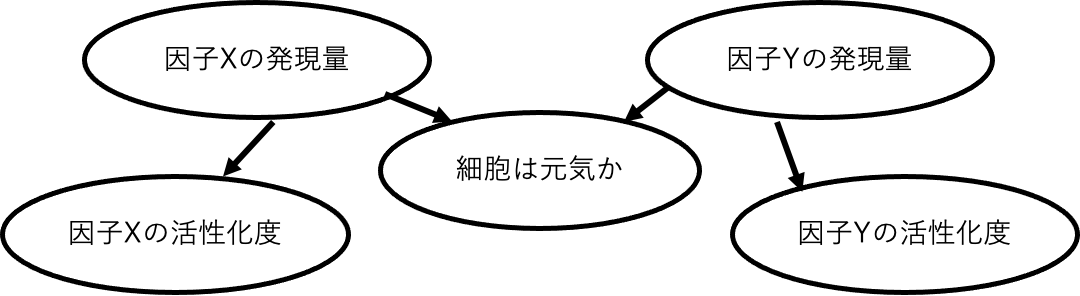
Fig.16 「細胞が元気か」がシグナル因子X, Yの発現量の結果になっている場合。シグナル因子の活性化度は発現量に依存するため元気な細胞を選ぶと、X, Y間の制御関係だけでなく、細胞が元気であるための要件による従属性を調べていることになりどちらの寄与がどれだけあるか分からない。
これは「シグナル因子X, Y間に制御関係がある可能性を示唆している」のか、「その相関パターンに従わない細胞も普通に現れるが、そういう細胞は元気がない(死ぬ、増殖が遅いなど)」のかという両方の可能性が生じることになる。この問題は結局様々な実験方法や細胞選定方法、多様な視点でのアプローチによって知見を蓄積させることによってしか、解決することはできないのかもしれない。ただ、条件を固定することにも固定しないことにもリスクが存在しているということ、そのリスクはどのようなものなのかは知っておくことに損はないだろう。
Reference
喫煙と肺がんリスク コホート研究 論文
Tomotaka Sobue, Seiichiro Yamamoto, Megumi Hara, Shizuka Sasazuki, Satoshi Sasaki, Shoichiro Tsugane; JPHC Study Group. Japanese Public Health Center, Cigarette smoking and subsequent risk of lung cancer by histologic type in middle-aged Japanese men and women: the JPHC study, Int J Cancer. 2002 May 10;99(2):245-51.
肺がん死亡率データ
データ出典
国立がん研究センターがん情報サービス「がん登録・統計」
国民生活基礎調査(厚生労働省大臣官房統計情報部) 国民生活基礎調査について
集計表ダウンロード
全国がん死亡データ(1958年~2021年)
喫煙率
データ出典
厚生労働省 国民健康・栄養調査
集計表
公益財団法人 健康・体力づくり事業財団
健康ネット 最新たばこ情報 成人喫煙率
ランダムウォーク 見せかけの回帰 論文
C.W.J. Granger and P. Newbold, Spurious regressions in econometrics, Journal of Econometrics Volume 2, Issue 2, July 1974, Pages 111-120
その他
当記事は「Kyoto.bioinfo Advent Calendar 2022」の記事として執筆しております。内容はbioinfoに限りませんが。