ビジネスでよく使われるA/Bテストの結果を正しく判断する（統計的手法とベイズ推定による検証方法の比較）

はじめに

• A/Bテストを実施した際に、結果が明らかに大きな差が出ればいいのですが、大抵の場合は数%の差で「これは意味がある差なのか？偶然なのか、、、」という場面をよく見かけます。
• そこで本稿ではA/Bテストの結果を解釈する際に有用な方法を紹介します。
• 検証方法としては古典的な統計的仮説検討を利用した方法（カイ二乗検定とt検定）と比較的新しいベイズ推定を利用した方法を紹介します。
• それぞれの理論的な説明はWEB上でたくさんあるので、実装・活用にフォーカスした事例を紹介します。

サンプルデータの作成

• バリデーション群（施策や改善等の介入をしているグループ）とコントロール群（比較対象として何もしてないグループ）のサンプルデータを作成する
• 検証したい対象は「バリデーション群とコントロール群の結果に差があるのか」となる
• 単純な平均値の比較だと0.311(バリデーション群)と0.267(コントロール群)であり差が微妙である　（考え方によっては差は顕著です。その場合はそれぞれのpをよりシビアにしてテストしてみてください）

# 必要パッケージのインストール
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import pymc3 as pm
import scipy as sp

# サンプルデータの生成（バリデーション群とコントロール群）
val = np.random.binomial(n=1, p=0.3, size=1000)# Validation group
ctrl = np.random.binomial(n=1, p=0.26, size=1000)# Control group

# コンバージョンレート
cvr_val = val.sum() / len(val)
cvr_ctrl = ctrl.sum() / len(ctrl)
print("Control CV rate: :", cvr_ctrl,"Validation CV rate: :",  cvr_val)

Control CV rate: : 0.267 Validation CV rate: : 0.311

A/Bテスト結果の検証

統計的仮説検定（カイ二乗検定）

• カイ二乗検定は下記のような表形式をインプットに検定結果を返す

- p-valueが0.03なので統計的な優位差があると言える（有意水準5%とした場合）

# カイ二乗検定
cross_table = pd.DataFrame([pd.Series(val).value_counts(), pd.Series(ctrl).value_counts()], index=['Validation', 'Control'])

x2, p, dof, expected = sp.stats.chi2_contingency(cross_table)
print('P-value is ', p)

P-value is 0.03390985744

統計的仮説検定（t検定）

• t検定はarray型をインプットにできるので、それぞれの結果をそのままインプットとする
• 厳密にはF検定で等分散性を検証する必要があるのですが、同一環境でA/Bテストをしている為、分散は等しいと仮定する
• p-valueが0.029なので統計的な優位差があると言える（有意水準5%とした場合）

# t検定 (等分散を仮定)
res_t = sp.stats.ttest_ind(val, ctrl, equal_var = True)

P-value is 0.0299770927112

統計的仮説検定（ベイス推定）

• pyMCを利用してベイズ推定を活用したA/Bテストの結果を判断する
• with構文内で推定するモデルを指定し、30,000回のシミュレーションを実施する
• 推定したい分布に関して今回は事前知識がなかった場面を推定して、一様分布を設定している

with pm.Model() as model:
    # 推定する分布の指定（事前分布が分かっている場合はここで指定）
    theta_val = pm.Uniform("theta_val", lower=0, upper=1)
    theta_ctrl = pm.Uniform("theta_ctrl",lower=0, upper=1)
    # 介入効果(コントロール群とバリデーション群の差）
    diff = pm.Deterministic("diff", theta_val - theta_ctrl)
    # 観測値の分布の指定（今回はベルヌーイ分布）
    observed_val = pm.Bernoulli("obs_c", theta_val, observed=val)
    observed_ctrl = pm.Bernoulli("obs_t", theta_ctrl, observed=ctrl)
    # サンプリング実行
    step = pm.Metropolis()
    trace = pm.sample(30000, step=step, njobs=2)

• 上記を実行すると、推定変数であるtheta_valとtheta_ctrl、またその差分であるdiffの結果がtraceに格納されている
• それぞれを可視化して分布を視覚的に理解する

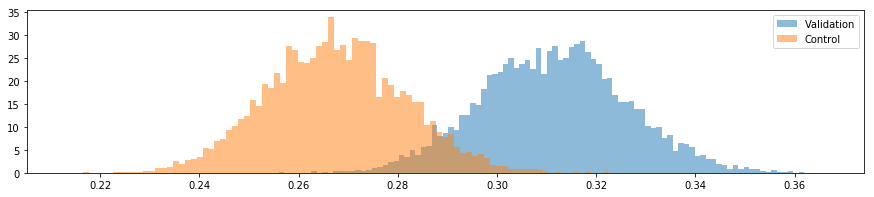
plt.figure(figsize=(15, 3))
plt.hist(trace['theta_val'], bins=100, density=True, alpha=0.5, label='Validation')
plt.hist(trace['theta_ctrl'], bins=100, density=True, alpha=0.5, label='Control')
plt.legend()
plt.show()

• サンプルデータを作成した際にバリデーション群はp=0.3、コントロール群はp=0.26としてので、中々良い推定結果となっている
• 次に介入効果（バリデーション群 - コントロール群）の結果も可視化する

plt.figure(figsize=(15, 3))
plt.hist(trace['diff'], bins=100, density=True, alpha=0.5, color='green')
plt.show()

• 分布は0以上の値をとっているので、介入効果はありと視覚的に判断できる
• またどの程度の介入効果があるのか、確率も算出することができる

threshhold = 0.05
prob = np.sum(trace['diff'] > threshhold) / len(trace['diff'])
print('介入によりCV rateが', threshhold, '以上の差がでる確率は', round(prob, 2)*100, '%となる')

介入によりCV rateが 0.05 以上の差がでる確率は 38.0 %となる

さいごに

• A/Bテストの効果検証に有効な方法論を紹介しました。
• 上記のサンプルケースは比較的大きな差があったので、統計的有意差もでましたが、現実のA/Bテストのデータではp値が綺麗に5%以下になることは稀です。
• その場合の結論は「統計的な有意差はない」であり、「介入効果はない」とまでは断言できない点がビジネス上の意思決定をする際に困ります。
• ベイズ推定を使うことで統計が分からないビジネスユーザーでも視覚的に介入効果が把握できたり、期待される介入効果と確率も推定できます。
• 明らかに差があるA/Bテストでは統計検定で結果を保証し、差が微妙な際はベイズ推定を活用して、リスクを把握したうえでビジネス上の意思決定をしていく、というのが実務上は効果的な使い分けだと思います
  。