#Section1:入力層~中間層
『
ディープラーニングは、結局何をやろうとしているか2行以内で述べよ。
また、次の中でどの値の最適化が最終目的か。
全て選べ。(1分)
①入力値[X] ②出力値[Y] ③重み[W] ④バイアス[b] ⑤総入力[u] ⑥中間層入力[z] ⑦学習率[ρ]
』
→
#####回答例:
誤差を最小化するパラメータを発見する事。
選択問題回答:③④
#####【考察】
最終的には出力値[Y]の値を正解の値に近づけていく事が目標だが、それを出力するために、重み[W]、バイアス[b]の最適化が目標になる。
ある入力[x]に対して、何らかの結果[y]を出力するタスクがあった場合、内部処理をfとした時に、y=f(x)と書ける。ディープラーニングは、この内部処理fと解釈する事も出来、重みとバイアスの最適化とは、内部処理fの最適化とも考える事が出来る。
『
次のネットワークを紙にかけ。
入力層:2ノード1層
中間層:3ノード2層
出力層:1ノード1層
(5分)
』
→
#####回答例:
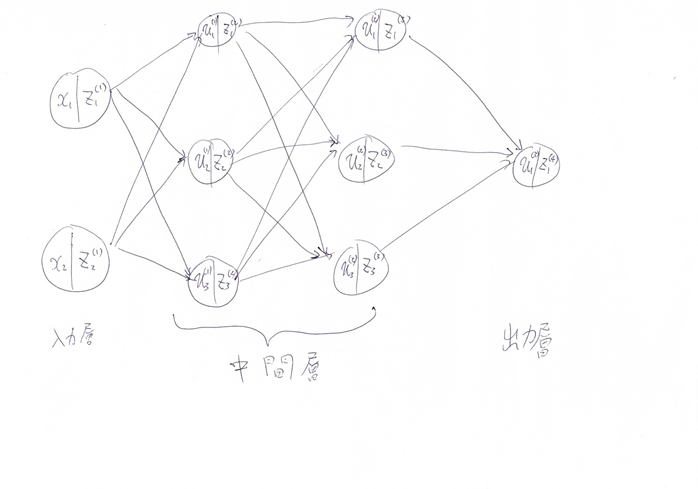
#####【考察】
ノードから次のノードに値を渡すときに、重みとバイアスが使われる。この重みとバイアスの最適化が学習の目標。
同一ノードでの、u→zについては、入力をuとした活性化関数fの出力がzになる。
『
この図式に動物分類の実例を入れてみよう。
(3分)
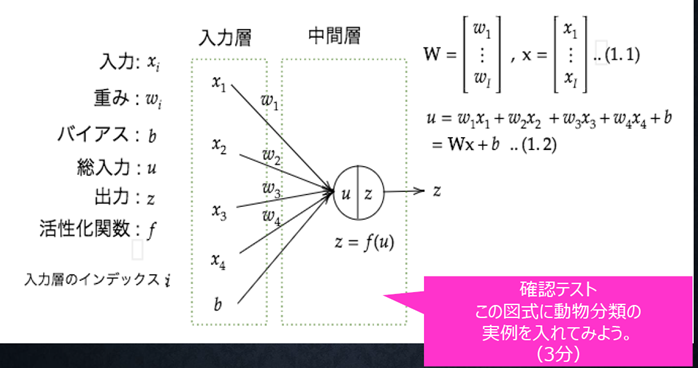
』
→
#####回答例:
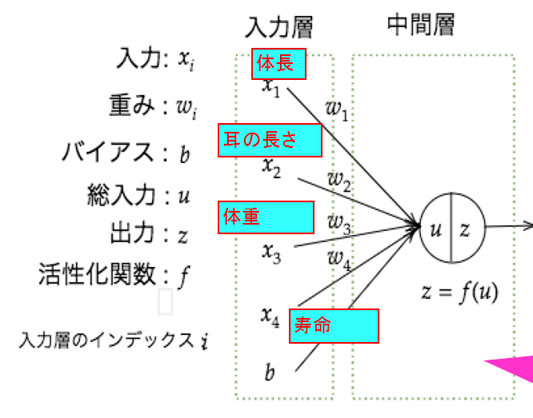
#####【考察】
入力値のxについては、何を与えるかについては、人間が判断する必要がある。
『
この数式をPythonで書け。
(3分)
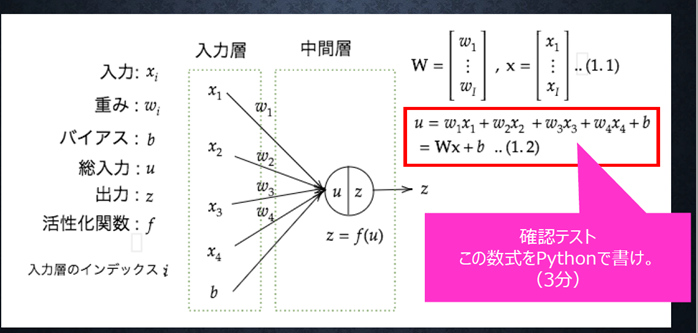
』
→
#####回答例:
import numpy as np
x1 = 1.0
x2 = 2.0
x3 = 3.0
x4 = 4.0
x = np.array([x1, x2, x3, x4])
w1 = 0.1
w2 = 0.2
w3 = 0.3
w4 = 0.4
W = np.array([w1, w2, w3, w4])
b = 0.1
u = np.dot(x, W.T) + b
print(u)
出力結果:3.1
#####【考察】
ベクトル同士の掛け算の和(Wx)を計算する時は、内積関数dotを利用する。
『
1-1のファイルから
中間層の出力を定義しているソースを抜き出せ。(3分)
』
→
#####回答例:
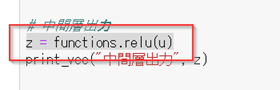
#####【考察】
総和uに対して、活性化関数はReLUを使って、zを出力している。
#Section2:活性化関数
『
線形と非線形の違いを図にかいて
簡易に説明せよ。
(6分)
』
→
#####回答例:
分類問題で考えると分かりやすい。
例えば、2つの特徴量から、2つのクラスを分類する場合、直線で分類する時に線形、
非直線で分類する時に非線形となる。
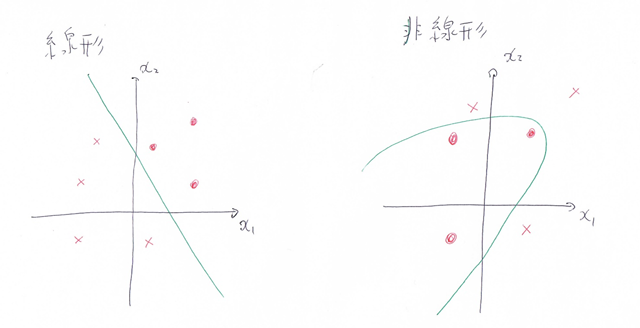
#####【考察】
・線形は、どちらかというと単純な分類(超平面で分割出来るもの)に使われる。
・非線形は、色々な種類が考えられるが、線形に比べて計算が難しくなる。
『
配布されたソースコードより
該当する箇所を抜き出せ。(3分)
』
→
#####回答例:
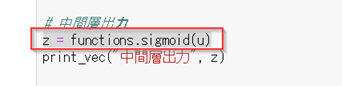
#####【考察】
複数ノードになって、単数ノードの時と、処理している事は変わらない。
各入力に対して、重みを掛けて、足し合わせて、バイアスを加えて、活性化関数に与える。
という一連の流れを、全てのノードに対して行っているだけ。
出力される値は、ノード数の数分、出力される。
#Section3:出力層(3-1 誤差関数)
『
・なぜ、引き算ではなく二乗するか述べよ。
・下式の1/2はどういう意味を持つか述べよ。
(2分)
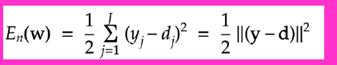
』
→
#####回答例および考察:
・引き算の場合、プラスの誤差とマイナスの誤差の両方が考えられる。例えば+1の誤差の結果と-1の誤差の結果があった場合、お互い打ち消しあって、誤差ゼロとなってしまう。そういった事を防ぐために二乗を行っている。
・1/2がある事で、E(w)を微分した時に、二乗の2と打ち消しあって、式がきれいになって、計算がしやすくなる。
#Section3:出力層(3-2 出力層の活性化関数)
『
①~③の数式に該当するソースコードを示し、一行づつ処理の説明をせよ。
(5分)

』
→
#####回答例:
def softmax(x): #ソフトマックス関数の宣言。①に該当する。引数のxは、uをリストとして受け取っている
if x.ndim == 2: #xの次元数が2の時
x = x.T #xを転置させる
x = x - np.max(x, axis=0) #各値についてXの最大値を引く
y = np.exp(x) / np.sum(np.exp(x), axis=0) # np.exp(x)が②、np.sum(np.exp(x), axis=0)が③に該当する
return y.T #yを転置させたものを返す
x = x - np.max(x) # オーバーフロー対策 各値についてXの最大値を引く
return np.exp(x) / np.sum(np.exp(x)) # np.exp(x)が②、np.sum(np.exp(x))が③に該当する
#####【考察】
数学の式をそのままではなく、実装時にはオーバーフロー対策などが必要になる。
引数についても、数式のそのまま渡すのではなく、リスト化して渡す事で、コードが見やすくなる(数式通り、引数をi,uで記述を行うと、呼び出し側でループしたりする必要が出てきて、コードが冗長になってしまう)。
『
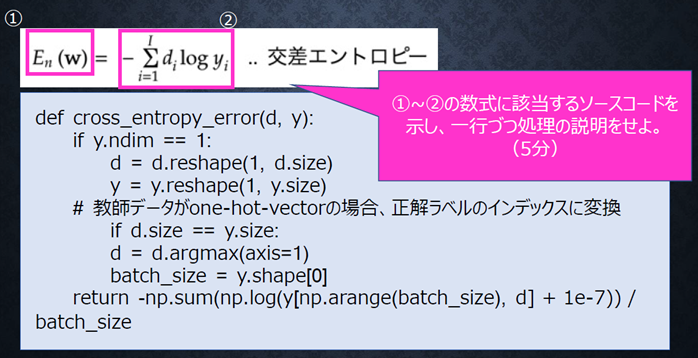
①~②の数式に該当するソースコードを示し、一行づつ処理を説明せよ。
(5分)
』
→
#####回答例:
def cross_entropy_error(d, y): #dを正解値、yを出力値として受け取っている。 ①に該当する
if y.ndim == 1: #yの次元が1の時
d = d.reshape(1, d.size) #dを1行のリストに変換
y = y.reshape(1, y.size) #yを1行のリストに変換
# 教師データがone-hot-vectorの場合、正解ラベルのインデックスに変換
if d.size == y.size: #dとyのサイズが同じ場合
d = d.argmax(axis=1) #正解値のインデックスに変換
batch_size = y.shape[0] #データ数を取得
return -np.sum(np.log(y[np.arange(batch_size), d] + 1e-7)) / batch_size #-np.sum(np.log(y[np.arange(batch_size), d] + 1e-7))の部分が②に該当する。
#####【考察】
実装時には、logの引数がゼロにならないように、1e-7のように、非常に小さい値を加えるなどの工夫が必要(ゼロの時に、-∞になってしまうため)。
#Section4:勾配降下法
『
該当するソースコードを探してみよう。
(1分)

』
→
#####回答例:
左側の式:
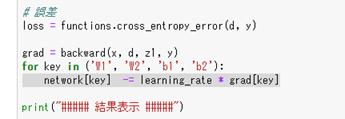
#####【考察】
∇を求めたりする細かい微分については、backward()関数の内部処理になるが、やっている事は、
今の値を勾配方向(誤差が少なくなる方向)に対して、パラメータWを更新している処理をしている。
『
オンライン学習とは何か
2行でまとめよ。(2分)
』
→
#####回答例:
新しくやってくる学習データに対して、
継続的に学習を続けていく学習方法。
#####【考察】
オンライン学習を行う事が出来れば、サービスとして、既に訓練されたパッケージを提供するだけではなく、提供した後も、継続して学習を続ける事が出来る。
『

この数式の意味を図に書いて説明せよ。
(5分)
』
→
#####回答例:
この式はミニバッチ勾配降下法のパラメータ更新の式になる。
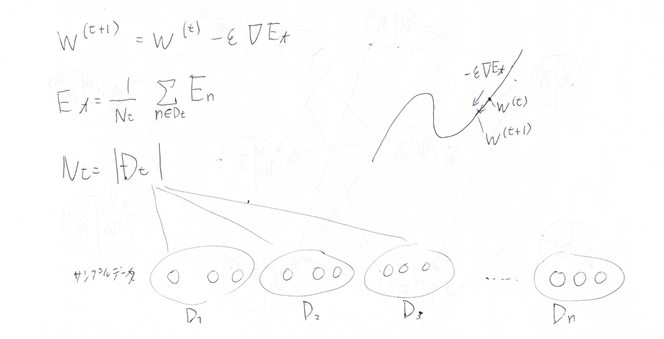
#####【考察】
全部の訓練データを、10~100個づつなどに分けて(ミニバッチ)、そのミニバッチごとにパラメータの更新を行う。
#Section5:誤差逆伝播法
『
誤差逆伝播法では不要な再帰的処理を避ける事が出来る。
既に行った計算結果を保持しいてるソースコードを抽出せよ。
(3分)
』
→1_2_back_propagation.py
#####回答例:
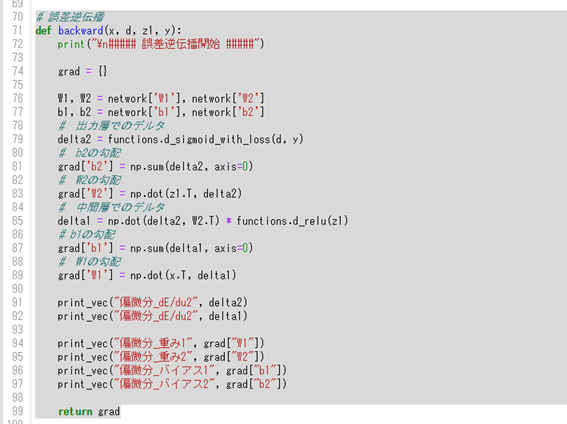
#####【考察】
delta2は1x2の行列になっているが、次に計算する時にベクトルにする必要があるので、
np.sum(delta2, axis=0)を使って、行列をベクトルに変換している。
実装時には、shapeをなど使って、形を確認しながら行うと整理される。
『
2つの空欄に該当するソースコードを探せ。
(3分)
1_3_stochastic_gradient_descent

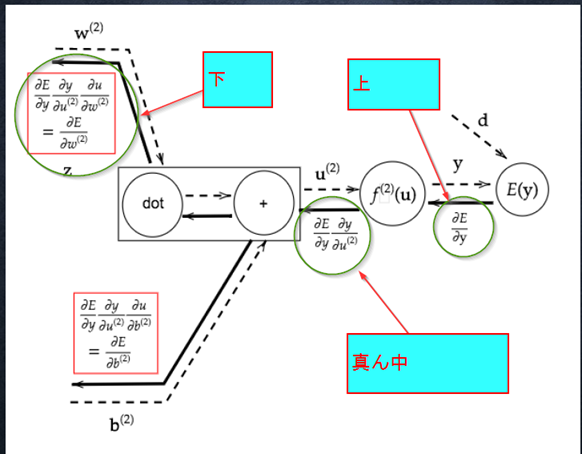
』
→
#####回答例:
上側:

#####【考察】
出力層側から入力層側に向かって、順番に勾配が求められているのが、コードから確認出来る。

