【線形回帰モデル】
1) 要点
| 学習種類 | 教師あり |
| タスク | 予測 |
| パラメータの推定 | 最小二乗法(最尤法) |
| モデル選択・評価 | ホールドアウト法 / 交差検証法 |
回帰問題:ある入力(数値)から出力(連続値)を予測する問題
線形回帰:データを直線で近似したもの。
線形回帰モデル:入力とm次元パラメータwの線形結合を出力するモデル。即ち
m次元パラメータ $w=(w_{1}, w_{2}, w_{3},…,w_{m})^{T}\in \mathbb{R}^{m}$ とした時に、
$\widehat{y}=w^{T}x+b= \sum_{j=0}^n w_j x_j + b$ ($\widehat{y}$:予測値)
であらわされるモデル。
ここで実際の正しい値yについては、下記の式であらわされる
y=Wx+ε
即ち、εは、実際の値yと、予測値$\widehat{y}$との誤差と考える事が出来る。
この誤差εを小さければ小さいほど、良いモデル という事が言える。
このm次元の学習パラメータwは、最小二乗法により推定を行う。
このwの事を、重みとも言う(深層学習でも、学習により更新されるパラメータの事を重みという言葉で表現する)。
最小二乗法:学習データの平均二乗誤差を最小とするパラメータを検索する方法
ここで、平均二乗誤差とは、
平均二乗誤差(MSE):予測値と実際の値との誤差の二乗したもの。つまり値が小さいほど、誤差が少ないと言える。数式は次のように定義する:
$MSE=\dfrac {1}{n} \sum_{i=0}^n (\widehat{y_i} - y_i)^2$ (n:データ数)
式を見ると、2次関数になっているので、MSEの最小化とは、勾配が0(ゼロ)になる点を求める事になる。
2) ハンズオン
線形回帰を用いて、ボストン住宅の価格データを予測するモデルを作る。
データセット:boston house-price
https://archive.ics.uci.edu/ml/machine-learning-databases/housing/
レコード数:506
カラム数:14
カラムには、犯罪発生率、部屋数、1教師あたりの生徒の数、などの特徴と、今回正解データとなる、住宅価格がある。
以下、実行結果
データの読み込みを行い、読み込んだデータを確認します。
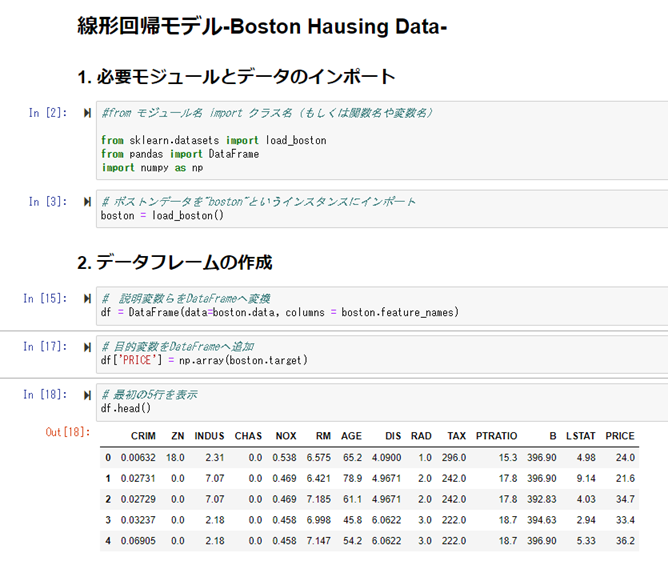
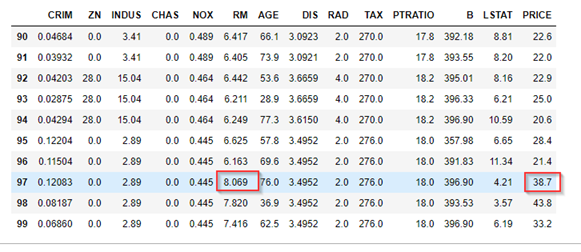
最後のカラム「PRICE」が予測したい住宅価格になる。
まずは、パラメータのRM(部屋数)のみから住宅価格を予測するモデルを作って、実際に予測してみる。
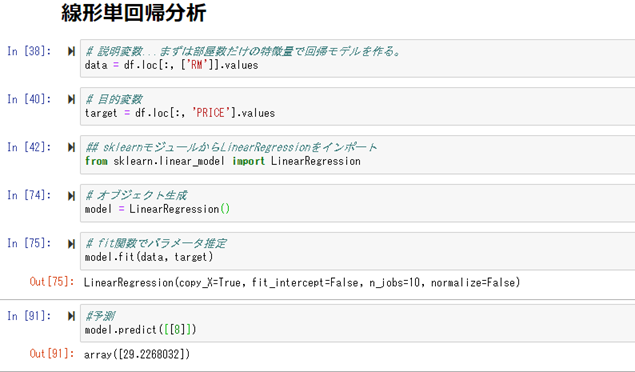
部屋数「8」にすると、「29.2」という数値が予測された。
実際のサンプルで部屋数「8.069」があるが、住宅価格「38.7」になっているので、「9.5」の差が大ある。
次に、部屋数(RM)に加えて、犯罪発生率(CRIM)も加えて予測を行ってみる。
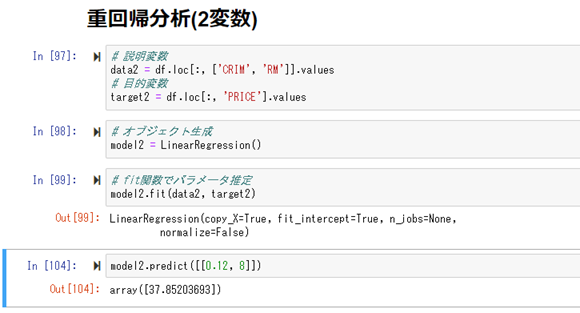
犯罪発生率「0.12」、部屋数「8」にすると、「37.8」という数値が予測された。
今度は実際の値38.7との差が、「0.9」となり、これは先ほどの、「9.5」よりも予測精度が高くなったと判断出来る。

最後に、学習後のモデルのパラメータを確認してみる。

【非線形回帰モデル】
1) 要点
| 学習種類 | 教師あり |
| タスク | 予測 |
| パラメータの推定 | 最小二乗法(最尤法) |
| モデル選択・評価 | ホールドアウト法 / 交差検証法 |
回帰問題:ある入力(数値)から出力(連続値)を予測する問題
非線形回帰:データを曲線で近似したもの。
非線形回帰モデル:入力とm次元パラメータwの線形結合を出力するモデル。
yについては、下記の式であらわされる:
$y_{i}= w_{0} + \sum_{i=1}^m w_j \phi_{j}(x_{i}) + \epsilon_i$
ここで、φ(x)は、基底関数と呼ばれる、既知の非線形関数。これから分かるように、線形回帰モデルとの違いが、この既定関数にある(それ以外は同じ意味になる)。
m次元の学習パラメータwは、回帰モデルと同様に、最小二乗法や最尤法により推定を行う。
φ(x)の例としては、
$\phi_{j}(x)=x^j$ 多項式
$\phi_{j}(x)=( - \dfrac{(x-\mu_j)^T(x-\mu_j)}{2h_j})$ ガウス型基底
などがある。
未学習/過学習について
未学習:学習データに対して、十分小さな誤差が得られない
過学習:小さな誤差は得られたが、テスト集合との誤差が大きい(学習データにフィットし過ぎた状態)。
というものが起きる。
過学習に対しては、正則化法で回避する方法がある(正則化し過ぎると未学習になる)。
正則化法:誤差関数MSEに対して、最小化を目指すところは同じだが、MSEの右辺に、ペナルティ項(正則化項)と呼ばれる項を加える。
非線形回帰の多項式の自由度が高ければ高いほど、テストデータにフィットし過ぎて、過学習を起こす可能性が高くなる。そこで、学習時に、学習パラメータの自由度を制約する。という意味がある。
モデル選択 ホールドアウト法/交差検証法(クロスバリデーション)について
ホールドアウト法:データを、学習用データと検証用データの2つに分割して、一度だけ学習を行う。
デメリットとしては、学習データが十分に多くない場合に、多くのデータで学習が行えない。
交差検証法:データを、学習用データと検証用データの2つに分けて、学習を行うところまでは、ホールド法と考え方は同じ。
一度目の学習後、再度データを学習用データと検証用データの2つに分割する。この時、一度目の時とは、異なる分割を行う。そして二度目の学習を行う。
二度目の学習後、再度データを学習用データと検証用データの2つに分割する。以下、このような事を何度か繰り返して学習を繰り返す。
つまり、交差検証法とは、データの水増しを行っている、と捉える事も出来る。これにより、学習データが十分に多くない場合でも、一見多くのデータを使って、学習を行う事が出来、より正確なモデルが出来上がる事になる。
2) ハンズオン
線形回帰モデルの時と同じものを使う。
同じ条件で部屋数のみの場合に住宅価格の予測がどうなるかを確認する。
線形回帰では、部屋数「8」にすると予測値が「29.2」となり、実際の値「38.7」から「9.5」の誤差があった。
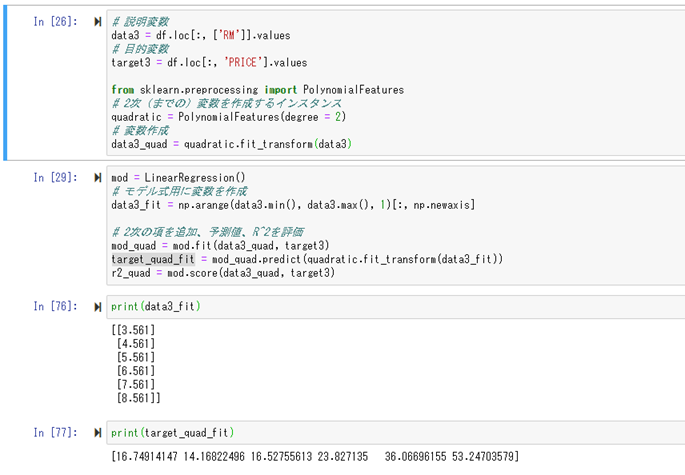
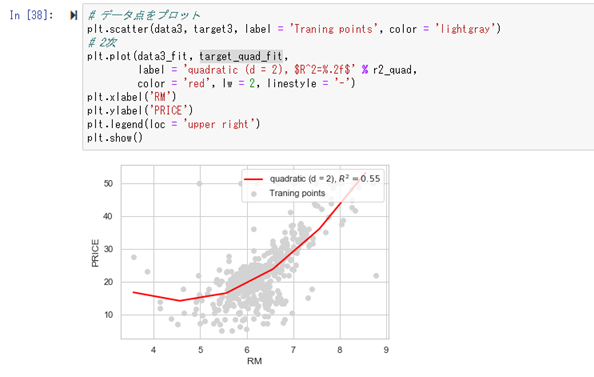
実際に部屋数「8」で計算した場合に、住宅価格「43.6」となり、正解「38.7」に対して「4.9」の誤差になる。
この値は、線形回帰モデルの時の誤差「9.5」に比べて良いと判断出来る。
【ロジスティクス回帰モデル】
1) 要点
| 学習種類 | 教師あり |
| タスク | 分類 |
| パラメータの推定 | 最尤法+確率的勾配降下法 |
| モデル選択・評価 | ホールドアウト法 / 交差検証法 |
上記の線形回帰モデル、非線形回帰モデルの連続数値の予測とは違い、
ロジスティクス回帰のタスクは、クラス分類になる。
クラス分類とは、入力データから予測する予測値が、連続値(スカラー)ではなく、どのカテゴリ(ラベル)に属するのかを判定するタスク。
ロジスティクス回帰モデルは、入力値と学習パラメータwの線形結合を取るのは、線形回帰の場合と同じ。即ち、
$\widehat{y}=w^{T}x+b= \sum_{j=1}^m w_j x_j + b$
とするところまでは同じ。ロジスティクス回帰モデルは、この後、シグモイド関数(ロジスティクス関数)と呼ばれる関数に、この出力 \hat{y} を入力とし与え、その結果、[0, 1]の範囲の値で、結果が出力される。シグモイド関数は、下記の式であらわされる:
$\sigma(x)=\dfrac{1}{1+e^{-ax}}$
つまり関数の定義から、シグモイド関数の出力は、$\sigma(x)\in \left[ 0,1\right]$の範囲になるので、この出力値をその分類に属する確率と考える事が出来る。
学習する時は、ある正解の分類に対して、σ(x)の値が「1」(確率1)になるように、学習パラメータを調整する事になる。
また、シグモイド関数の微分は、下記のようになっていて、自身で表現出来るという特徴がある:
$\dfrac{\partial \sigma(x)}{\partial x} = a \sigma(x)(1- \sigma (x))$
ロジスティクス回帰では、パラメータの推定に、上で説明した線形回帰モデルで使った最小二乗法とは異なる方法、最尤法または確率的勾配降下法を使う。
最尤法
尤度:あるデータを得た時に、分布のパラメータが特定の値である事がどれほどありえそうかを表現したもの。
確率は、パラメータを固定して入力データが変化しますが、尤度は、入力データを固定して、パラメータが変化する。
尤度関数は、Y=1となる確率をpとした時に、$P(Y=t|x) = p^t (1-p)^{1-t}$とすると、
Y=1になるn個のデータについて、結果を掛け合わせたものになる。即ち、
$L(w_0, w_1, w_2, … , w_m) = \prod_{i=1}^{n} p_{i}^{y_i}(1-p_i)^{1-y_i}$
となる。式の定義から、この値が最大になるように、学習パラメータwを推定する事が目的になる。
但し、この式を直接的に最大にする事が難しいため、次の式E(w)を定義する:
$E(w_0, w_1, w_2, … , w_m)=-logL(w_0, w_1, w_2, … , w_m)=- \sum_{i=1}^{n} \left\{ t_n log(p_i) + (1-t_i) log(1-p_i) \right\} $
このE(w)の式にすると、L(w)に比べて計算しやすくなる。
またE(w)の定義から、L(w)のlogをとったものに、マイナスを掛けているので、
L(w)を最大化する事と、E(w)を最小化する事は、同じ意味として考える事が出来る。
確率的勾配降下法(SGD)
勾配降下法:反復学習により学習パラメータを、逐次的に更新するアプローチ。
学習パラメータwとバイアスbは、以下の式で更新
される:
$w^{(k+1)} = w^{(k)} - \eta \dfrac{\partial E(w, b)}{\partial w}$
$b^{(k+1)} = b^{(k)} - \eta \dfrac{\partial E(w, b)}{\partial b}$
ここで、η:学習率 と呼ばれる、ハイパーパラメータ。
また、各式の右辺は、次のように計算する事が出来る:
$\dfrac{\partial E(w, b)}{\partial w} = - \sum_{i=1}^{n} (t_i - y_i)x_i$
$\dfrac{\partial E(w, b)}{\partial b} = - \sum_{i=1}^{n} (t_i - p_i)$
このように、学習パラメータを逐次的に更新する事が出来る。
但し、学習パラメータを更新するのに,n個全てのデータに対する和を求める必要があるため、nが巨大になった場合、データをメモリに載せる要領が足りなくなったり、計算時間が膨大に掛かるなどの問題がある。
そこで、確率的勾配降下法というものを利用して、この問題を解決する。
確率的勾配降下法:考え方は勾配降下法と同じだが、
n個全てのデータではなく、1つずつランダムに選択して、学習パラメータを更新する。
勾配降下法で学習パラメータを1回更新するのと同じ計算量で、パラメータをn回更新させる事が出来る。
類似の方法で、ミニバッチ勾配降下法と呼ばれるものもある。
こちらは、n個のデータをm個(m<n)の、小さなかたまりに分けて学習を行う方法。
ロジスティクス回帰では、タスクが分類になるので、線形回帰モデルや非線形回帰モデルとは異なる評価を行う必要がある。評価方法については、いくつかあるので以下に説明する。
正解率
モデルが正解した数と、データ数の割合で評価をする。即ち、
$(正解率) = \dfrac{(正解数)}{(データ数)}$
つまり、正解した確率という事になる。
全問正解した場合は、「1」になり、全問不正解だった場合は、「0」になる。
ただし、この正解率の評価方法については、分類したいクラスに大きな偏りがある場合は、偏りのあるデータに対して、単純な正解率は余り意味をなさない事が多いので、注意する必要がある。
以下、説明のため、次の言葉を定義する:
「TP」(True Positive) :モデルが正と予測して、実際に正だった数
「FP」(False Positive) :モデルが誤と予測して、実際は正だった数
「FN」(False Negative) :モデルが正と予測して、実際は誤だった数
「TN」(True Negative) :モデルが誤と予測して、実際は誤だった数
定義より、TPとTNが正解数の合計という事になる。
この定義より、正解率は、次の式で表す事も出来る:
$(正解率)= \dfrac{TP+TN}{TP+FN+FP+TN}$
正解率に変わる分類の評価方法がいくつかある。それら値は以下の通りになる:
$(適合率[Precision])= \dfrac{TP}{TP+FP}$
$(再現率[Recall])= \dfrac{TP}{TP+FN}$
$(F値[F-measure])= 2 \times \dfrac{(Precision) \times (Recall)}{(Precision) + (Recall)}$
それぞれ以下の特徴がある。
適合率:見逃しが多くても、より正確な予測をしたい時に有効(例:メールのスパム判定など)。
再現率:誤りが多くても、抜け漏れを少なくしたい時に有効(例:病気の診断など)。
F値:適合率と再現率の調和平均をとったもの。
2) ハンズオン
ロジスティクス回帰を用いて、タイタニックの生存者を予測するモデルを作る。
データセット:Titanic
https://www.kaggle.com/c/titanic
レコード数:891(training)+417(test)
カラム数:11
カラムには、性別、年齢、運賃、などの特徴と、今回正解データとなる、生存可否がある。
以下、実行結果
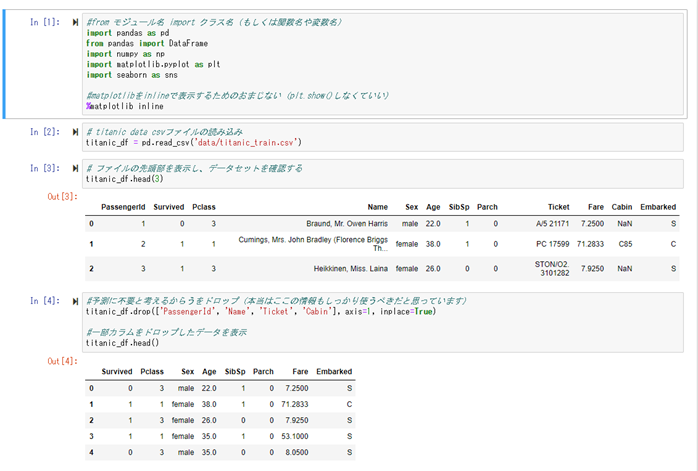
データの読み込みを行い、読み込んだデータを確認します。
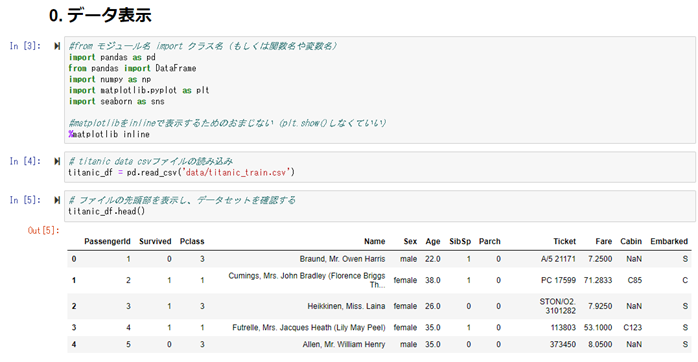
次に、カラムの中で、不要と思われるID、名前などの情報を除外します。
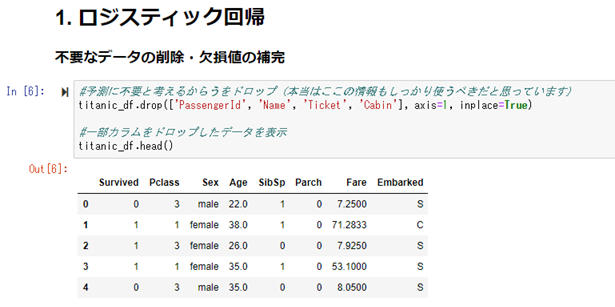
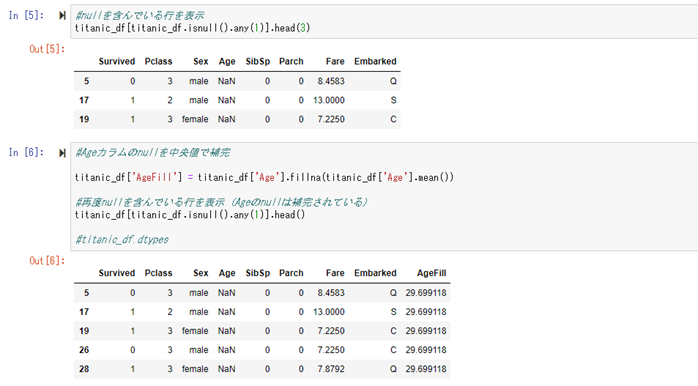
残っている特徴の中で、年齢(Age)にデータの欠損があるものを確認。
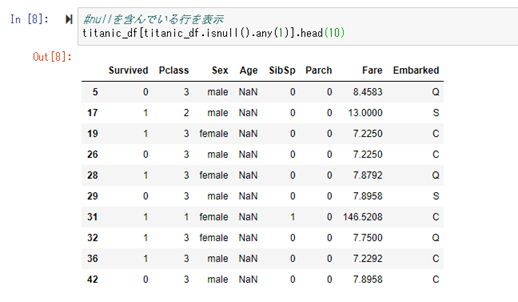
欠損している年齢を補完。補完した値は、新たに「AgeFill」のカラムに追加する。
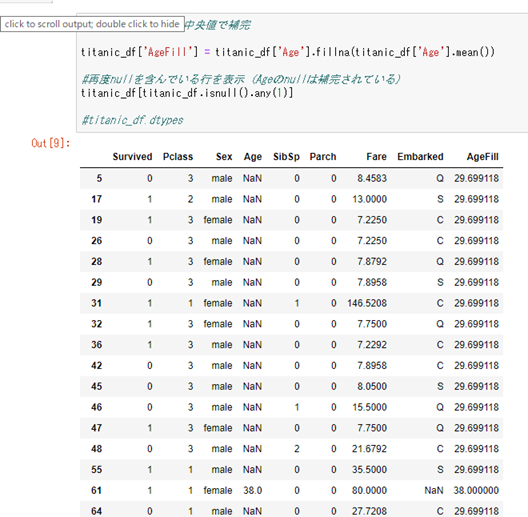
まずは、特徴を運賃(Fare)だけに絞って、ロジスティクス回帰モデルを作る。
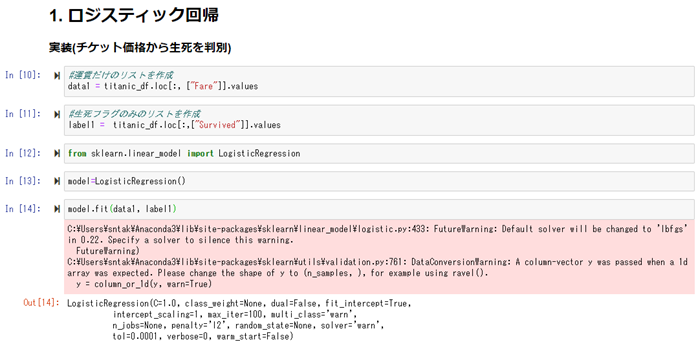
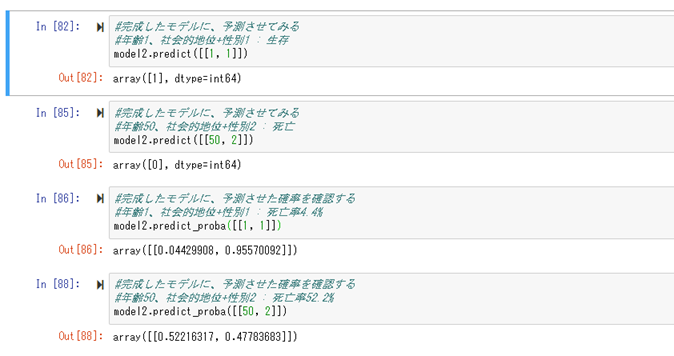
出来上がったモデルに対して予測を行ってみる。
運賃60ドルの人は、死亡。運賃70ドルの人は、生存。という予測モデルになっている事が確認出来る。

また死亡/生存の確率も確認する事が出来る。

今度は、2変数で予測モデルを作成してみます。
年齢と(社会的地位+性別)の2変数を使います。
年齢は、先ほど補完を行った「AgeFill」を使います。
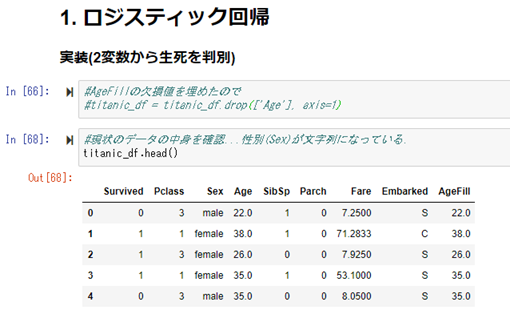
次に、性別(Sex)が文字列となっているので、[男性(male)]=1, [女性(female)]=0を割り当て、
その値を、新たに作成するカラムGenderに割り当てます。
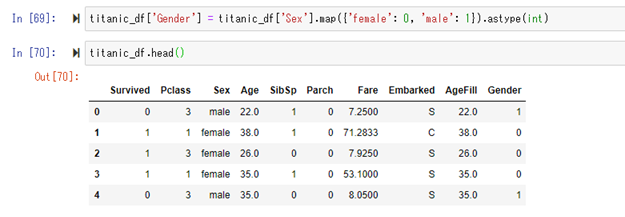
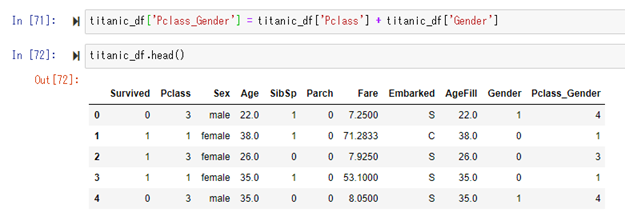
続いて、社会的地位(Pclass)に、先ほど割り当てたGenderの値を足します。
足した値は、新たに作成するカラムPclass_Genderに割り当てます。
この2つの特徴を足す行為については、男性よりも女性の方が生き残りやすい、
社会的地位は、高い方が、低い方よりも生き残りやすい(Pclassは小さい値の方が、社会的地位が高い)。
という事前の予測(人間が行う)から来ている行為です。
つまり、Pclass_Genderの値が小さければ小さい方が、生き残る可能性が高くなるだろう、という事になります。
データから、不要になったカラムを取り除きます。
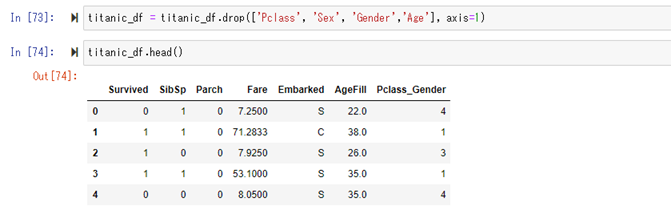
モデル作成前ですが、
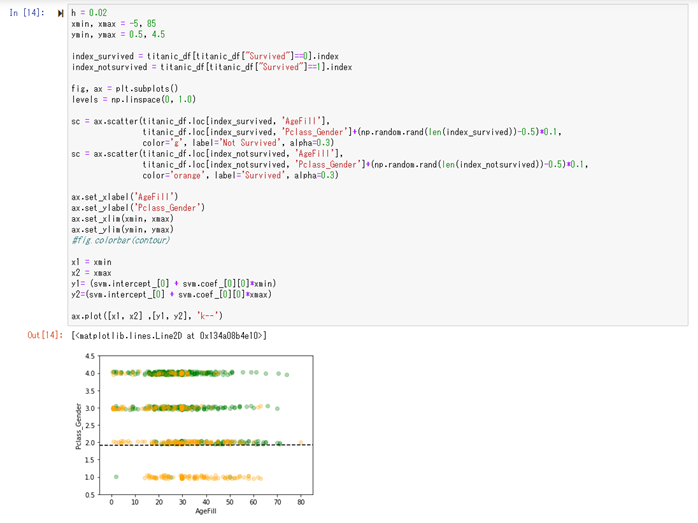
この状態で、データを一度プロットしてみます。
横軸が年齢(AgeFill)、縦軸が社会的地位+性別
青色のプロットが生存、赤色のプロットが死亡
を表しています。
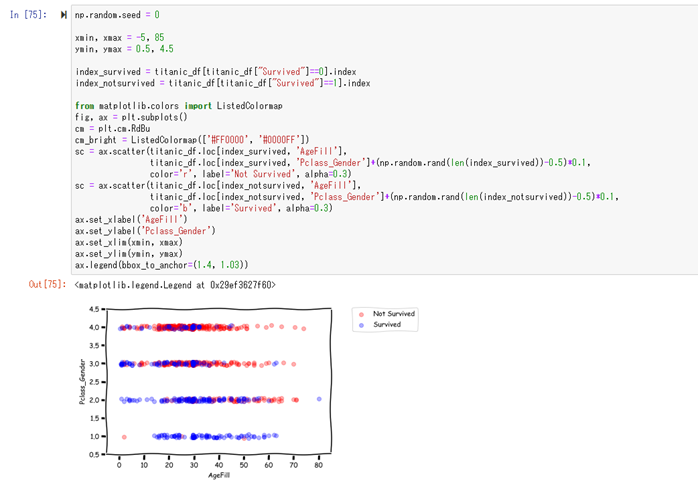
プロットされたものを見て見ると、縦軸(Pclass_Gender)の値が低いほど、生存率が高くなり、
横軸(AgeFill)の値が低いほど、生存率が高くなっているのが視覚的に確認する事が出来ます。
右下から右上に行くに従って、生存率が低くなっているのが確認出来ます。
続いて、これら2変数のロジスティクス回帰モデルを作成します。
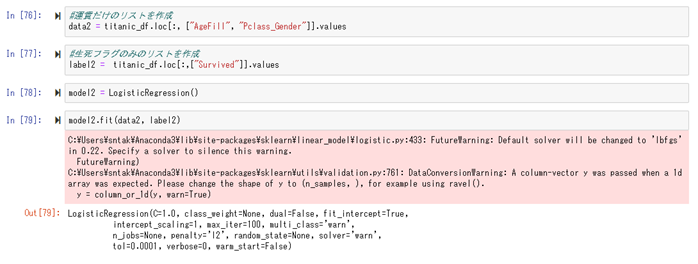
出来上がったモデルに対して、先ほどと同じように、死亡/生存の予測と、確率を確認する事が出来ます。
次に、出来上がったモデルを可視化してみる。
左上から右下に向かって、黒い点線が、予測モデルの生存/死亡の境界値を示している。
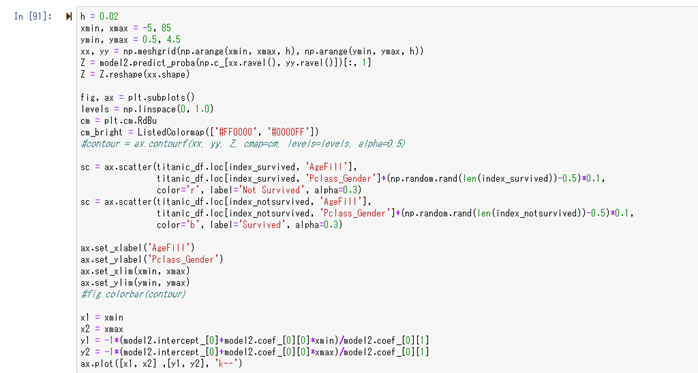
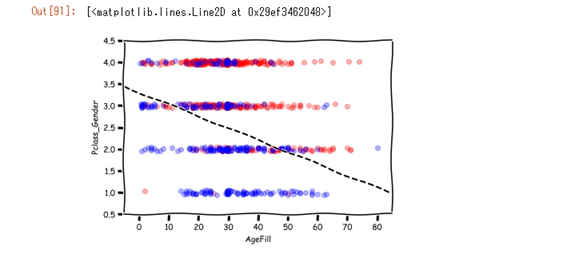
最後にモデルの評価を行う。
1変数の場合と、2変数の場合、の2パターンの評価を行う。
まずは、トレーニングデータとテストデータに分割を行う。
今回はトレーニングデータ80%、テストデータ20%にする。
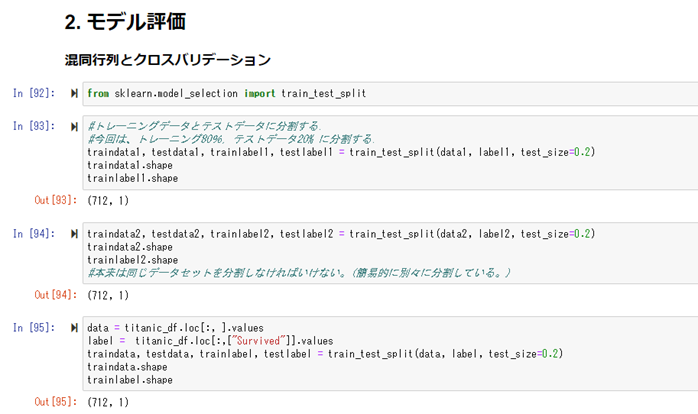
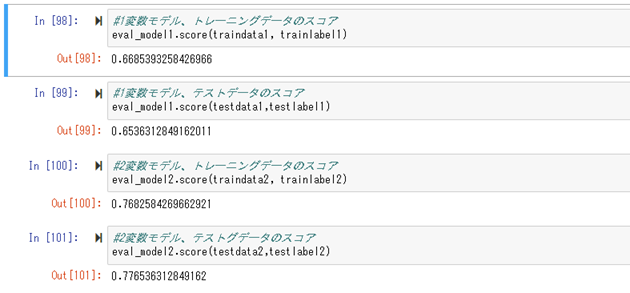
モデルを作成し、トレーニングデータデータで学習させ、テストデータで予測を行う。
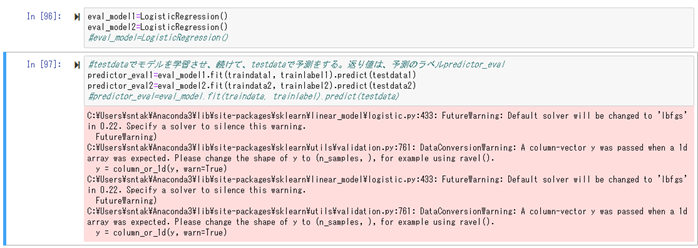
学習したモデルの、スコアを確認する。
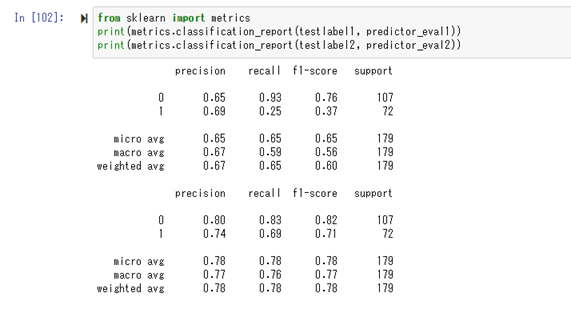
適合率、再現率、F値などを確認。
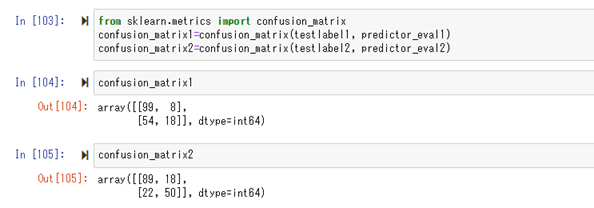
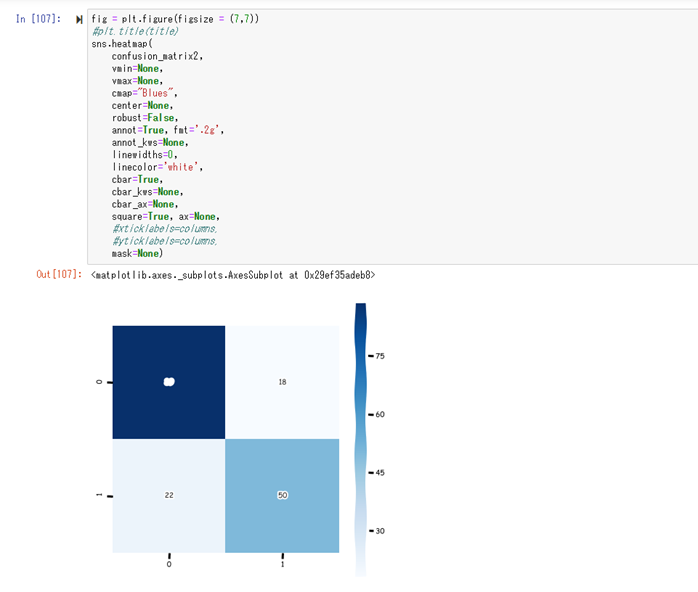
混同行列(Confusion Matrix)形式で、結果を確認する。
行列は$\begin{pmatrix} TP & FP \\ FN & TN \end{pmatrix}$ になっている。2変数の方が、正解数が多い事が分かる(1変数に比べて、死亡した人を多く正解している)。
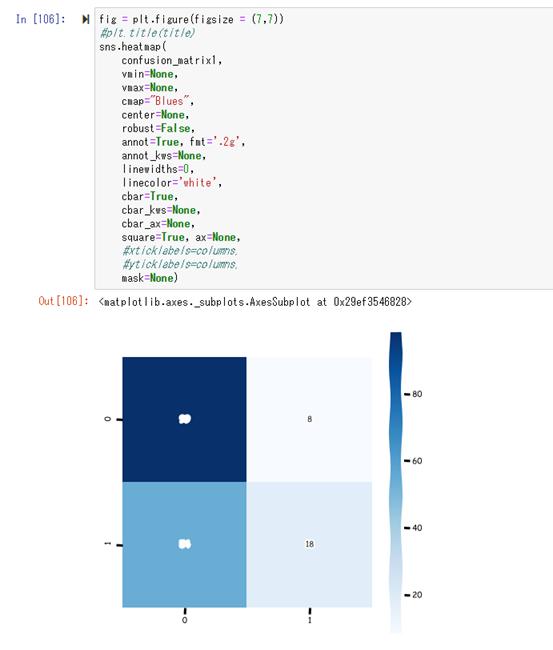
このままだと分かりづらいので、可視化を行う。
色が濃い方が、分布が多い。
つまり左上、右下の領域の色が濃く、左下、右上の色が薄い結果が望ましい。
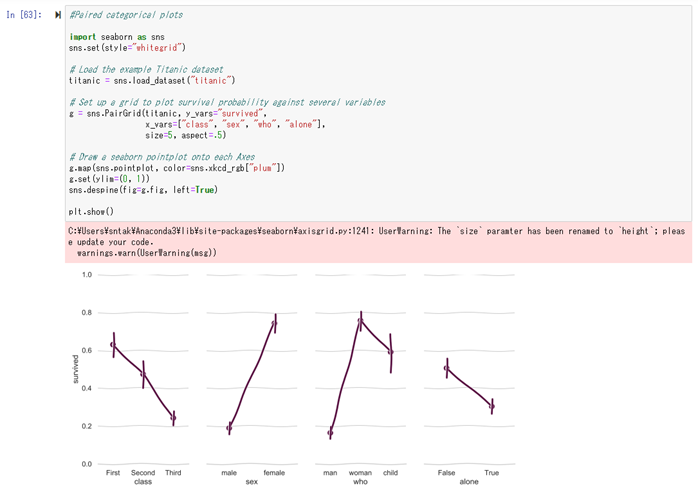
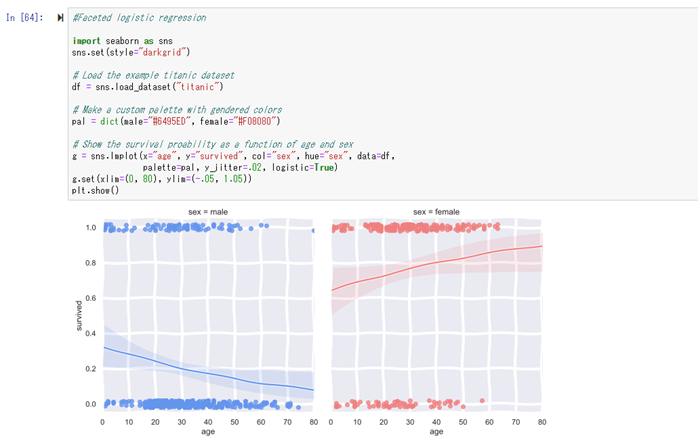
【主成分分析(PCA)】
1) 要点
| 学習種類 | 教師なし |
| タスク | クラスタリング |
| パラメータの推定 | 固有値分解 |
| モデル選択・評価 | 無し |
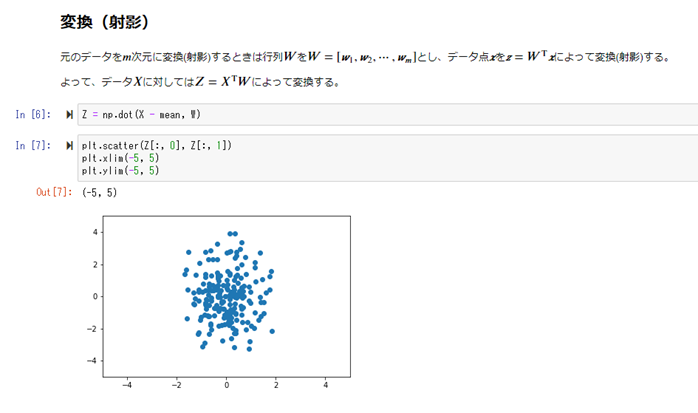
主成分分析(PCA)とは、多種類の入力パラメータを持つデータを、少数個の指標のまとめる方法(入力パラメータの次元を削減させる)。
相関が高い入力パラメータを複数含むような冗長な高次元空間を、冗長性の少ない低次元空間に落とす事を行う。
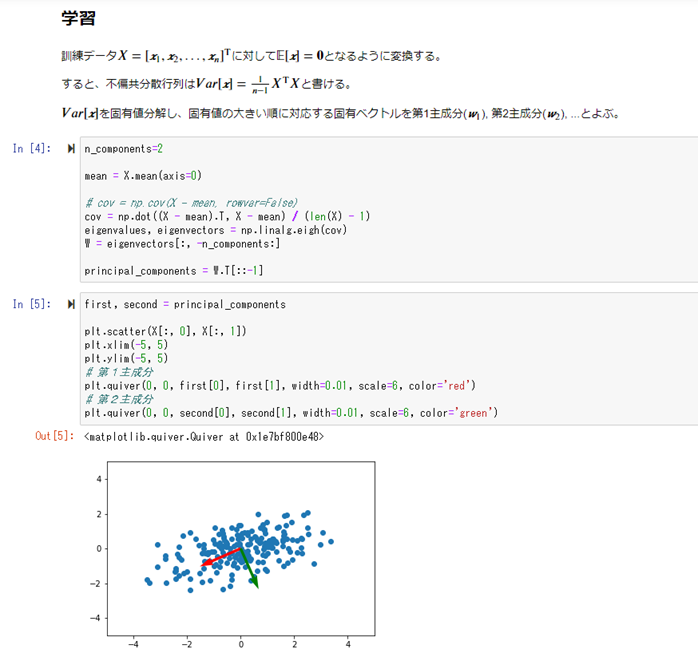
学習データの分散が最大になる方向への線形変換を求める方法。
次元を減らす事で、視覚的に人間の目にも理解出来るように可視化する事が可能になる。
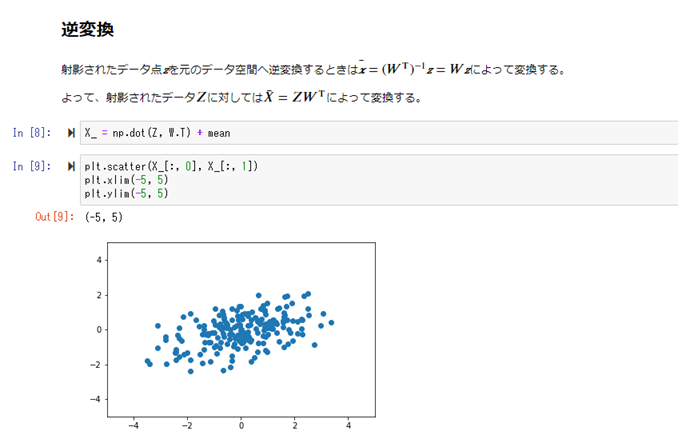
2) ハンズオン
【アルゴリズム】
1) 要点
| K近傍法 | |
|---|---|
| 学習種類 | 教師あり |
| タスク | 分類 |
| パラメータの推定 | k-近傍法) |
| モデル選択・評価 | ホールドアウト法 / 交差検証法 |
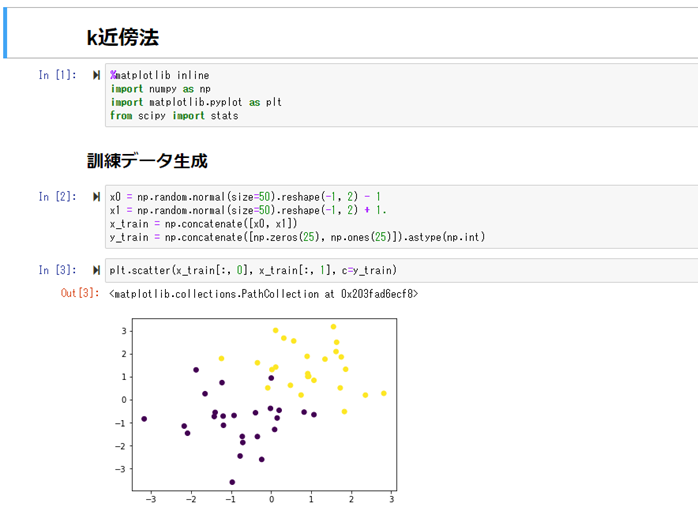
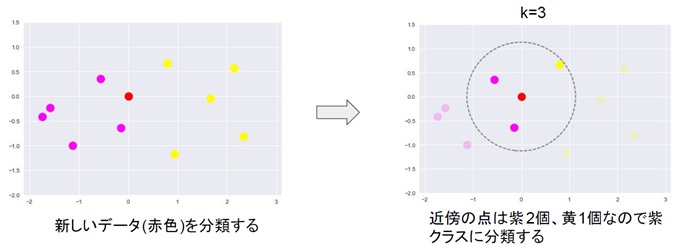
k近傍法(kNN)
k近傍法(kNN):
タスクはクラス分類。非常に単純なアルゴリズム。
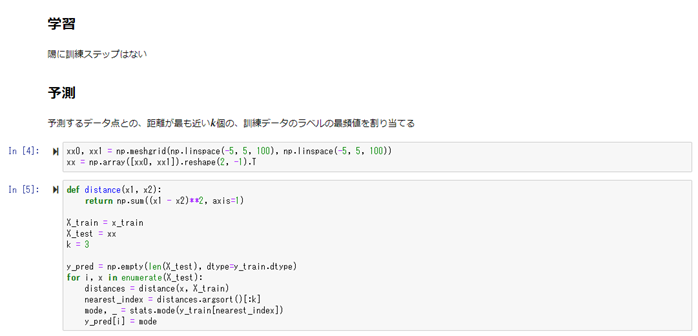
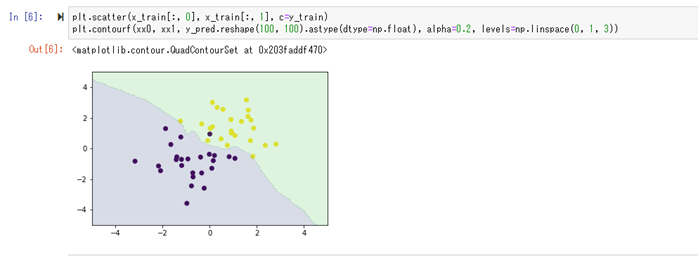
新しく得られたデータを中心にして、最も距離の近い、既存の座標の点k個を選び出し、そのk個の点の中で最も多かったクラスに分類する。
kの値については、事前に決める必要がある。
| K平均法 | |
|---|---|
| 学習種類 | 教師なし |
| タスク | クラスタリング |
| パラメータの推定 | k-平均クラスタリング |
| モデル選択・評価 | 無し |
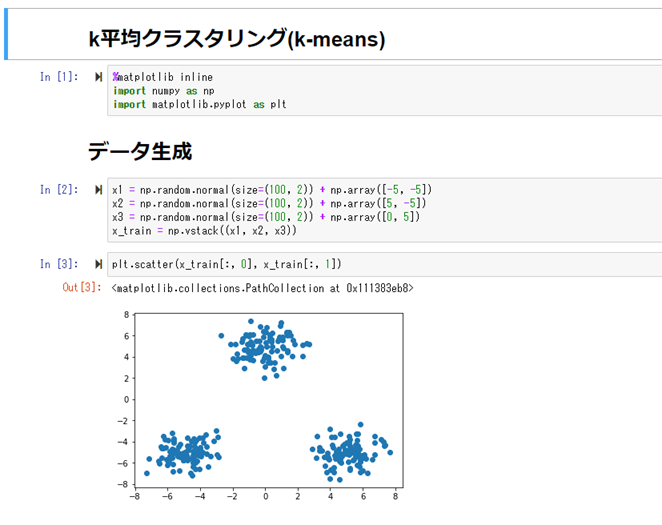
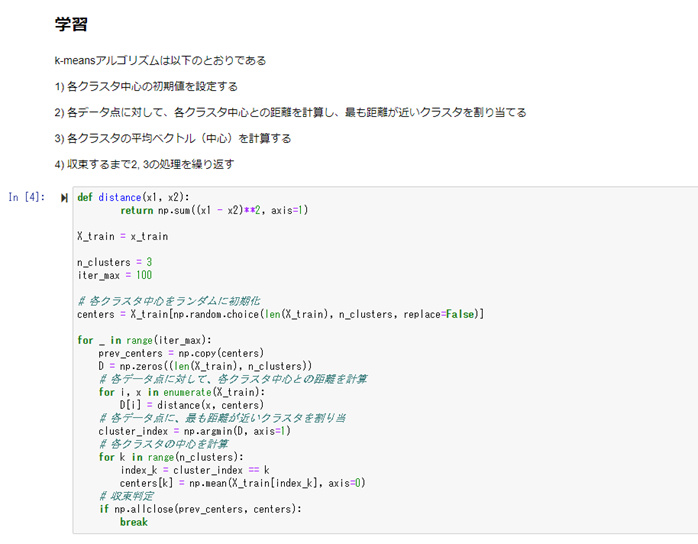
k平均法(k-means)
タスクは、クラスタリング。教師なし学習。
事前に結果のクラスがある訳ではなく、学習によって、データをk個のクラスに分類する。
kは事前に人間が決める必要がある(学習によって決まる訳ではない)。
初期値で、各クラスタの中心座標(k個)をランダムで決め、各クラスタの中心座標を、学習によって更新していく手法。
初期値がランダムで選ばれる事で、学習の結果が変わってくる事が知られている。
従って、異なった初期値で学習を複数回行い、評価関数の最も良いものを結果として採用する。
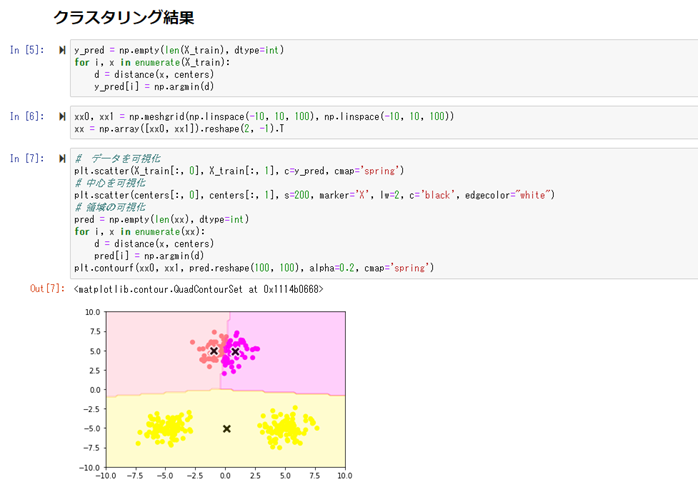
2) ハンズオン
【サポートベクターマシーン(SVM)】
1) 要点
| 学習種類 | 教師あり |
| タスク | 分類 |
| パラメータの推定 | マージン最大化 |
| モデル選択・評価 | ホールドアウト法 / 交差検証法 |
2クラス分類のための機械学習の手法(回帰に使われる事もある)。
線形モデルを使って、2クラスを分類する識別面を求める方法(マージンを最大化する識別面)。
出力は、正負で2クラスを分類する。
$y=w^Tx+b$
とした時に、yを入力とする次の関数の正負で分類を決定する:
$sign(y) = \begin{cases}+1 (y>0) \\ -1 (otherwise) \end{cases}$
このwを学習していく事がSVMの目標となる。
線形的な超平面と、学習データ(点)との距離を求める事になるので、最適かは下記を満たすwを求める事に帰着される:
$min_{w,b} \dfrac{1}{2} \left|| w \right|| ^{2}$
条件:$t_i(w^T x_i +b) \geq 1, (i=1, 2, …,n)$
但し、線形的に分類するため、分類出来ないクラスが出て来る。その場合は、ペナルティを課す事で対応する方法や、学習データを高次元にマッピングして超平面で分類するなどの対処方法がある。
ソフトマージンSVM(ペナルティ)
誤差を許容して、誤差に対してペナルティを与える。
最大マージン内に入るデータや、誤分類されたデータに対して、次の誤差変数ξを導入する:
$\xi_i = 1 - t_i(w^T x + b) > 0$
ここでξは、条件を満たさない程度を表しているので、小さい方が望ましい事になる。
この値を、上記SVMマージン最大化の式に加えます。即ち、
$min_{w,b} \dfrac{1}{2} \left|| w \right|| ^{2} + C \sum_{i=1}^{n} \xi_i$
条件:$t_i(w^T x_i +b) \geq 1 - \xi_i, (i=1, 2, …,n), (\xi_i \geq 0)$
ここでCは、トレードオフを制御するパラメータで、Cが大きければ影響が大きく、Cが小さければ影響が少なくなる。
カーネル関数(高次元に写像)
そのままの学習データでは、線形分離出来ない場合に、高次元の特徴空間にマッピングして、線形分離を行う手法。
学習時は、カーネルトリックと呼ばれる方法を使い、複雑な非線形変換を求める事を避ける事が出来る。