はじめに
前回、線形回帰とカーネル回帰について書いた記事 の続きのような感じで、主成分分析とカーネル主成分分析を取り上げます。
PRMLやその他の本を読んでいて難しく感じたカーネル主成分分析の導出について、普通の書き方とは別の視点でまとめてみます。
自分なりに考えた結果、特異値分解の知識を背景にすれば、主成分分析とカーネル主成分分析の関係がすっきり理解できると思うのですが、本やネットで言及しているものが見当たらないので、記事にしました。
まとめると、以下のようなことです。
- 主成分分析は共分散行列の固有値問題に帰着する
- カーネル主成分分析はグラム行列の固有値問題に帰着する
- これらはどちらも計画行列の特異値分解を(それぞれ別の方面から)解いていることに相当する。
主成分分析
データベクトル $x$ が $N$ サンプルあるとします。データをそのまま使ってもよいのですが、カーネル法のことも考えると、より一般的に、$M$ 個の基底関数 $\phi_i(x)$ で特徴量ベクトル $\phi(x)$ に直します。
$$\phi(x) := \begin{pmatrix}
\phi_1(x) \
\vdots \
\phi_M(x)
\end{pmatrix}
$$
計画行列 $\Phi$ を $N$ サンプル分の特徴量ベクトルを並べたものとして定義します。
$$\Phi := \begin{pmatrix}
\phi(x_1)^T \
\vdots \
\phi(x_N)^T \
\end{pmatrix}
=\begin{pmatrix}
\phi_1(x_1) &\cdots & \phi_M(x_1) \
\vdots & & \vdots \
\phi_1(x_N) &\cdots & \phi_M(x_N) \
\end{pmatrix}$$
$N$ サンプルの特徴量ベクトルを $M$ 次元特徴量空間上にプロットしたものを考えます。このとき分散が大きくなるような方向を求めるのが主成分分析です。
説明は省きますが、これは、共分散行列の固有値問題になります。固有値の大きさが、その固有ベクトル方向の分散に相当します。
あらかじめ平均が0となるようにデータを中心化しておくものとすると、共分散行列は $Φ^TΦ /N$ と書けるので、結局、主成分分析は $M$ 次正方かつ対称な行列 $Φ^TΦ$ の固有値問題に帰着します。
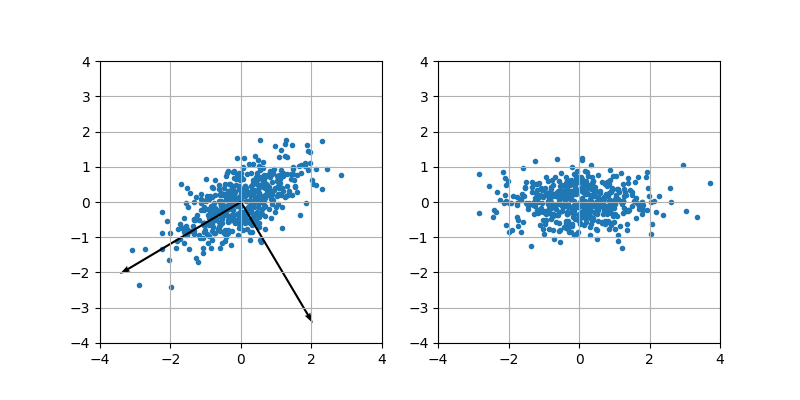
2次元正規分布でデータを生成して主成分を計算した例を示します。最初のグラフに固有ベクトルの方向を書き入れました。2番目のグラフが主成分表示で、次元削減する場合はこれのx軸成分のみをとれば良いことになります。
class Pca:
# データを入力して主成分ベクトルを計算する
# データは平均0を前提とする
# shape(X)=(N,M)
def fit(self, X):
# 共分散行列
Sigma = np.dot(X.T, X)
vals, vecs = np.linalg.eigh(Sigma)
# eighは固有値の昇順で出力される
vals = vals[::-1]
vecs = vecs[:, ::-1]
# v[:,i] : 第i主成分の固有ベクトル
self.v = np.array(vecs) # (M,M)
# x を主成分表示にして返す
# shape(x)=(n_samples, M)
# n: 抽出する主成分の数
def transform(self, x, n):
return np.dot(x, self.v[:, :n]) # (n_samples,M)x(M,n)=(n_samples,n)
(数学的準備) 固有値分解
特異値分解に入る前に、対称行列の固有値分解について天下り的にまとめておきます。
固有値分解
対称行列 $A$ は対角行列 $Λ$, 直交行列 $P$ を使って
$$A=PΛP^T$$
と書けます。これを対称行列 $A$ の固有値分解と呼びます。
固有値と固有ベクトル
上式の両辺に右から $P$ を掛けると、$AP=PΛ$ となります。
これは、$Λ$ の対角成分を $λ_i$, $P$ の列ベクトルを $p_i$ とすると、
$$Ap_i=λ_ip_i$$
と書けます。$λ_i$ を固有値、$p_i$ を固有ベクトルと呼びます。
(数学的準備) 特異値分解
固有値分解は正方行列に対してしか適用できません。
一般の長方行列に対しては、特異値分解という方法があります。
ここでも天下りですが、先ほどの固有値分解の場合と対応するように、まとめてみます。
特異値分解
行列 $Φ$ ($N\times M$, 階数 $r$)は対角行列 $Σ$ と 直交行列 $U, V$ を使って、
$$Φ=UΣV^T$$
- $U$ : $N\times r$ 直交行列
- $Σ$ : $r \times r$ 対角行列
- $V$ : $M\times r$ 直交行列
と書けます。1
特異値と特異ベクトル
$Σ$ の対角成分を $σ_i$ とし、$V, U$ の列ベクトルを $v_i, u_i$ とします。
上式の両辺に右から $V$ を掛けると、$ΦV=UΣ$ となります。
また、転置をとった後、右から $U$ を掛けると $Φ^TU=VΣ$ となります。
これらをまとめて書くと、
$$\begin{cases}
Φv_i=σ_iu_i \
Φ^Tu_i=σ_iv_i
\end{cases}
$$
となります2。$σ_i$ を特異値、$v_i$ を右特異ベクトル、$u_i$ を左特異ベクトルと呼びます。
右特異ベクトルが入力側の空間、左特異ベクトルが出力側の空間にあることを意識することが重要です。
特異値分解を行うには、2通りの解き方があります。
(解き方1) $Φ^TΦ$ の固有値問題を解く
$Φ^TΦ = (VΣ^TU^T) (UΣV^T) = VΣ^2V^T$ なので、$Φ^TΦ$ は固有値 $σ_i^2$ で右特異ベクトル $v_i$ が固有ベクトルとなることが分かります。
$$Φ^TΦv_i=σ_i^2v_i$$
したがって、$Φ^TΦ$ の固有値問題を解けば、特異値 $σ_i$ と右特異ベクトル $v_i$ が得られます。あとは、$Φv_i=σ_iu_i$ にこれらを代入して、$u_i$ について解けば左特異ベクトルが得られます。
(解き方2) $ΦΦ^T$ の固有値問題を解く
$ΦΦ^T = (UΣV^T) (VΣ^TU^T) = UΣ^2U^T$ なので、$ΦΦ^T$ は固有値 $σ_i^2$ で左特異ベクトル $u_i$ が固有ベクトルとなることが分かります。
$$ΦΦ^Tu_i=σ_i^2u_i$$
先ほどとは逆に、左特異ベクトル $u_i$ が先に得られます。あとは、$Φ^Tu_i=σ_iv_i$ にこれらを代入して、$v_i$ について解けば右特異ベクトルが得られます。
カーネル主成分分析
主成分分析は $Φ^TΦ$ の固有値問題でした。
これは $Φ$ の特異値問題の解き方1(の前半部分)でもあります。
カーネル主成分分析では特異値問題の解き方2を使い、$ΦΦ^T$ の固有値問題を解きます。
$ΦΦ^T$ は以下のように、特徴量ベクトルの内積を成分とする行列で、グラム行列と呼ばれます。
$$K_{ij}:=(ΦΦ^T)_{ij} = \phi(x_i)^T\phi(x_j)$$
カーネル主成分分析では、グラム行列 $K$ の固有値 $σ_i^2$, 固有ベクトル $a_i$ を計算します3。$a_i$ は 行列 $Φ$ の左特異ベクトル(この節では文字を $a$ にします)であり、対応する右特異ベクトルを $v_i$ として、特異ベクトル間の関係
$$\begin{cases}
Φv_i=σ_ia_i \
Φ^Ta_i=σ_iv_i
\end{cases}
$$
が成り立ちます。4
データ $x$ の特徴量ベクトル $\phi(x)$ の主成分は、右特異ベクトル $v_i$ 方向成分なので、$v_i$ への射影成分(内積)をとって
$$ \phi_{\mathrm{PCA}i}(x) = \phi(x)^Tv_i$$
ですが、特異ベクトル間の関係を使って左特異ベクトルで書き直すと、
$$\phi_{\mathrm{PCA}i}(x) = \frac{1}{σ_i}\phi(x)^TΦ^Ta_i$$
となります。これを計算するとカーネル関数が使える形になることが分かります。
$$\phi_{\mathrm{PCA}i}(x) = \frac{1}{σ_i}{\phi}(x)^TΦ^Ta_i
= \frac{1}{σ_i}\sum_{n=1}^N a_{i,n} \phi(x)^T\phi(x_n) = \frac{1}{σ_i}\sum_{n=1}^N a_{i, n} k(x, x_n )
$$
元データ $\phi(x_n)$ についてはより簡単に、
$$\phi_{\mathrm{PCA}i}(x_n) = \phi(x_n)^Tv_i = (Φv_i)_n = (σ_ia_i)_n$$
のようにベクトル $σ_ia_i$ の 第 $n$ 成分として得られます。
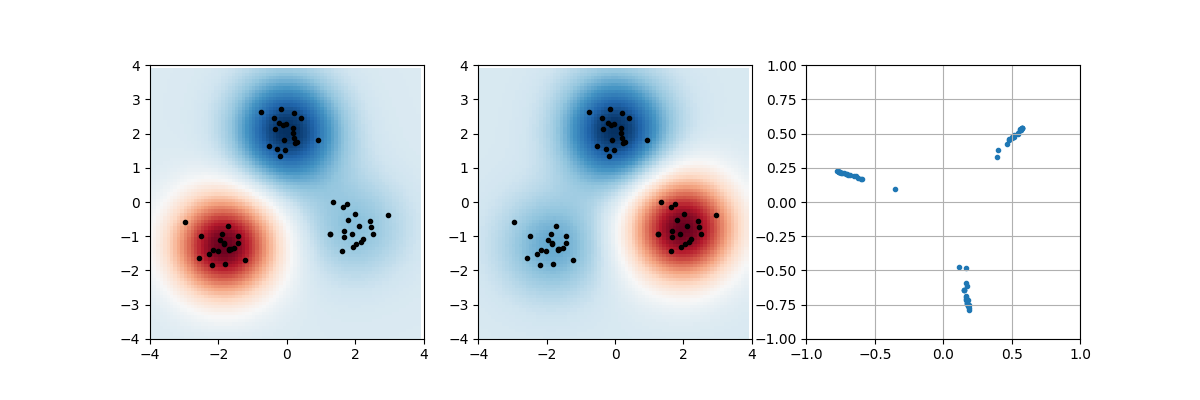
3種類の2次元正規分布でデータを生成し、カーネル主成分分析を行った例を示します。カーネル関数としてガウスカーネルを使いました。コードでは、グラム行列の中心化だけscikit-learnのライブラリ関数を使いました。
1つ目の図は元の特徴量空間でデータをプロットするとともに、第1主成分を色で表示しています。2つ目の図は第2主成分です。3つ目の図は主成分をxy軸にとってプロットしています。
from sklearn.preprocessing import KernelCenterer
class KernelPca:
# beta: ガウスカーネルパラメータ
def __init__(self, beta):
self.beta = beta
self.centerer = KernelCenterer()
# gauss kernel
def __kernel(self, x1, x2):
return np.exp(-self.beta * np.linalg.norm(x1 - x2)**2)
# データを入力して主成分ベクトルを計算する
# shape(X) = (N, M)
# n: 抽出する主成分の数
def fit_transform(self, X, n):
self.X = X
# グラム行列
N = X.shape[0]
K = np.array(
[[self.__kernel(X[i], X[j]) for j in range(N)] for i in range(N)])
# 中心化
K = self.centerer.fit_transform(K)
# eighは固有値の昇順で出力される
vals, vecs = np.linalg.eigh(K)
vals = vals[::-1]
vecs = vecs[:, ::-1]
# 特異値と左特異ベクトル、上位n個
self.sigma = np.sqrt(vals[:n]) # (n)
self.a = np.array(vecs[:, :n]) # (N,n)
return self.sigma * self.a # (N,n)
# xの主成分表示を返す
# shape(x)=(Nx, M)
def transform(self, x):
# グラム行列
N = self.X.shape[0]
Nx = x.shape[0]
K = np.array(
[[self.__kernel(x[i], self.X[j]) for j in range(N)] for i in range(Nx)]
) # (Nx,N)
# 中心化
K = self.centerer.transform(K)
# 主成分を計算
return K.dot(self.a) / self.sigma # (Nx,n)
まとめ
主成分分析とカーネル主成分分析を対比的に書くと以下のようになります。
- 主成分分析 : 共分散行列 $Φ^TΦ$, $M$ 次元の特徴量空間の固有値問題
- カーネル主成分分析 : グラム行列 $ΦΦ^T$, $N$ 次元のデータ空間の固有値問題
長方行列 $Φ$ を扱う問題で、$Φ^TΦ$, $ΦΦ^T$ という2種類の正方行列が鍵となるのは、一般逆行列の問題でも同じです。
そして、どちらの行列を使うかといえば、基本的に次数が小さくなる方を選べばよいのです。つまり、縦長なら $Φ^TΦ$, 横長なら $ΦΦ^T$ を選ぶということです。なぜかといえば、行列 $Φ$ の階数がそれより大きくなることはないからです。
参考文献
- C. M. ビショップ『パターン認識と機械学習 下』 : §12.1 に主成分分析、§12.3 にカーネル主成分分析が記載。定式化の仕方は基本的にこれに合わせています。
- 金谷健一『これなら分かる応用数学教室』 : §6.2~§6.3に、題材は画像ですが、この記事で書いた話と数学的に全く同じ構造の話が載っています。
- ストラング『線形代数イントロダクション』: 線形代数の教科書ですが、工学系への応用が意識されています。特異値分解についても解説があります。
注意点として、純粋数学系の本だと固有値問題からジョルダン標準形に進むのが一般的で、特異値分解はあまり書かれていません。そのため、応用寄りな本を探すことになります。
-
特異値分解には階数 $r$ を使わない分解の仕方もあります。 ↩
-
固有ベクトルもそうですが、特異ベクトルには大きさの任意性と符号の任意性が残ります。この式は、大きさについては右特異ベクトルと左特異ベクトルをともに正規化すること、符号については、$Φv_i$ と $u_i$ が同じ符号を持つ約束を前提にしています。 ↩
-
主成分分析前にデータの平均を 0 にすることに対応して、カーネル法を使う場合、グラム行列には中心化処理が必要ですが、ここでは説明を省きました。 ↩
-
PRMLでは少し違って、$Φv_i = σ_i^2a_i$, $Φ^Ta_i = v_i$ となっています。これは先に注釈で書いた、特異ベクトルの大きさの決め方の違いによるものです。 ↩