機械学習モデルの局所的な説明手法を比較してみる

この記事はBrainPad Advent Calendar2021　13日目の記事となります。

アナリティクスサービス部の佐々木です。今回は機械学習モデルの局所的な説明手法について、interpretable machine learningという本を参考に解説していこうと思います。

はじめに

自分は21卒として入社し、研修を経て半年ほどデータサイエンティストとして仕事を行なってきましたが、ビジネスの現場において機械学習モデルの解釈が求められることは多いなと感じています。

入社以来、需要予測の案件に関わっているのですが、「なぜこの商品は需要はこの値になるのか」「なぜこのカテゴリの商品は予測精度が悪化しているのか」といったような質問をクライアントの方から頂く場面がありました。

学生の頃は、機械学習モデルの解釈性は新薬開発やクレジットカードの審査など、人命、生活に大きく関わる場面で用いられるくらいかと思っていましたが、機械学習モデルは導入コストも高いですし、モデルの予測結果によって売上や利益が大きく変わってくる以上その影響力は大きく、ドメイン関係なくモデルの解釈性は重要視されることになります。

とはいえ、線形回帰など解釈性の高いモデルを用いれば良いかというとそういう訳でもなく、予測精度も機械学習モデルの重要視すべき点であるため、予測精度は高いが複雑で解釈性の低い、所謂ブラックボックスなモデルが採用されるケースが多く、その上で解釈性が求められます。

複雑で解釈性の低いモデルを用いながら、モデルの解釈を可能にする。一見、無理難題に思えるタスクですが、モデルに依存せずに予測の解釈のできる手法の研究は活発に進んでおり、ビジネスの現場でも使われてきていると感じます。

ブレインパッドの社員でも機械学習の解釈可能性に興味を持つ人は多く、有志でinterpretable machine learningという解釈可能な機械学習について広範なトピックを扱った本の輪読会を開催していました。

今回は、自分の実体験から、特定の入力に対するモデルの局所的な説明が求められる場面が多いと感じているので、この記事では、局所的な説明を可能にする手法として、

• LIME
• Anchor
• SHAP

の3つの概要、実装方法を輪読会で扱っていた本を参考に取り上げたいと思います。

LIME

LIMEのアイデアはとても直感的です。ある説明したいインスタンスがあった時に、そのインスタンス周辺のブラックボックスなモデルの挙動を解釈可能なモデルで近似し、近似した解釈可能なモデルを用いて説明を行います。
具体的には、LIMEは次のようなステップを踏んで、あるインスタンスについての説明が行われます。

• 説明したいインスタンスを選択
• 説明したいインスタンスに摂動（インスタンスにノイズを加え新しいサンプルを作成）加え、新しく作成したサンプルに対するブラックボックスなモデルの予測を行う
• 新しいインスタンスとブラックボックスなモデルの予測結果を教師データとして解釈可能なモデルを学習（この際、説明したいインスタンスとの近さに応じて各サンプルを重み付け）
• 解釈可能なモデルによって予測を説明

数式としては、解釈可能な制約を加えたモデルは以下のように表されます。

\newcommand{\argmax}{\mathop{\rm arg~max}\limits}
\newcommand{\argmin}{\mathop{\rm arg~min}\limits}

explanation(x) = \argmin_{g \in G} L(f, g, \pi_{x}) + \Omega(g)

• $x$: 説明したいインスタンス
• $f$: ブラックボックスなモデル
• $G$: 解釈可能なモデルの集合
• $g$: 解釈可能なモデル
• $\pi_{x}$: 近似度
• $L$: 損失関数
• $\Omega$: モデルの複雑度

インスタンス$x$に対する解釈可能なモデルは、ブラックボックスなモデル$f$の予測を近似するように損失$L$（平均二乗誤差など）を最小化するように学習します。その際、サンプルは近似度$\pi_{x}$による重み付け、モデルの複雑度に対する制約$\Omega$（決定木であれば木の深さ、線形回帰であればnon-zeroな重みの数）が考慮されます。
LIMEの短所でもあるのですが、この近似度$\pi_{x}$の決め方は実装者に委ねられています。近傍を定義するのにLIMEでは指数平滑化カーネルが用いられているのですが、カーネル幅を変えることで説明したいインスタンス周辺のサンプルの近似度が変わり、（カーネル幅が小さいと説明したいインスタンスに非常に近いサンプルしか考慮されず、大きいと遠いサンプルも考慮されます）
近似度をどのように設定するかによってLIMEでは説明が大きく変わることがあるので注意が必要です。

Anchor

AnchorはLIME同様、説明したいインスタンス周辺のブラックボックスなモデルの挙動を近似する方法を提供しますが、そのアプローチは少し異なっています。
LIMEでは摂動空間のサンプルに解釈可能なモデルを当てはめましたが、Anchorでは何らかの決定規則を獲得することを目的とします。
ここでいう決定規則とはIF-THENルールのことで、「もし気温が高く、湿度が高ければ、アイスが多く売れる」というように、何らかの条件を満たせば結果が決まる、という形で説明ができるので、解釈が非常に分かりやすいです。
数式としてはAnchorは以下のように表されます。

\mathbb

E_{D_{x}(z \mid A)}[1_{f(x)=f(z)}] \geq \tau, A(x)=1

• $x$: 説明したいインスタンス
• $f$: ブラックボックスなモデル
• $z$: 摂動空間のインスタンス
• $A$: 決定規則, $A(x)=1$は$x$の特徴量の値が$A$によって定義された決定規則を満たす時1となる。
• $D_{x}(\cdot | A)$: $A$を満たす$x$の近傍データの分布
• $\tau$: 精度の閾値

説明したいインスタンスがAnchor $A$を満たし、$A$を満たす摂動空間のインスタンスのブラックボックスなモデルの予測値が説明したいインスタンスの予測値と一致する割合が閾値$\tau$を超えていれば、$A$はAnchorの定義を満たします。

下図はある2値分類のタスクに適用した際の異なる2つのケースについてLIMEとAnchorを比較したものです（$+, -$はそれぞれ説明したいインスタンス、$D$は摂動空間全体を表しています）。
　

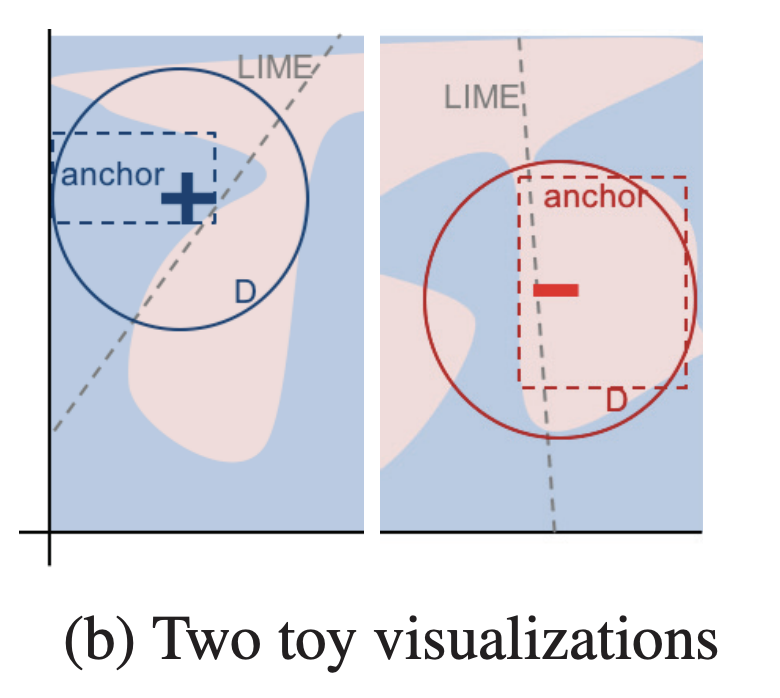
図はRibeiro, Singh, and Guestrin (2018)より引用

LIMEの場合、ブラックボックスモデルを近似する解釈可能なモデルが得られますが、その結果がどれだけ信頼できるものか示す指標はありません。一方Anchorの場合、摂動空間のインスタンスの中でどれだけの割合のインスタンスに適用できるか（点線で囲まれた領域）が指標として活用できます。

この指標のことをカバレッジと呼び、カバレッジは摂動空間に適用できるAnchorの確率として定義されます。

cov(A) = \mathbb E_{D(z)}[A(z)]

実際にAnchorを求める際には、全ての連続空間や大規模な入力空間では決定規則を満たす摂動空間のインスタンス全てについてブラックボックスモデルで評価し精度を算出することは難しいので、著者らは$0 \leq \delta \leq 1$のパラメータを使用して確率的な定義を導入します。

P(prec(A) \geq \tau) \geq 1 - \delta \quad with \quad prec(A) = \mathbb E_{D_{x}(z \mid A)}[1_{f(x)=f(z)}]

この定義を満たすAnchorの中で、モデルの入力空間の大部分に適用できるルールを見つけたいため、先ほど導入したカバレッジの概念を用いて、求めたいAnchorの最終的な定義は以下のようになります。

\max_{A \, s.t. \, P(prec(A) \geq \tau) \geq 1 - \delta} cov(A)

このようなAnchorを見つけるアルゴリズムの詳細については、説明すると長くなってしまうため、是非interpretable machine learning　5.8節を参照していただければと思います。

SHAP

SHAPは説明したいインスタンスの予測値と、全てのインスタンスの平均との間の差分を、各特徴量ごとの貢献度に分配する手法です。SHAPによる説明では協力ゲーム理論におけるシャープレイ値を計算します。

シャープレイ値は協力ゲーム理論の文脈では総報酬額に対する貢献度に応じて、ゲームの参加者に報酬の分配を公平に行う方法です。機械学習の文脈では、「ゲーム」があるインスタンスに対する予測タスク、「報酬」が全てのインスタンスの予測値の平均とあるインスタンスの予測値との差分、「プレイヤー」が各特徴量の値になります。

数式的な表現としては、以下のように表されます。

\phi_{j}(val) = \sum_{S \subseteq \lbrace{x_1, ..., {x_p}\rbrace \backslash \lbrace{x_j}\rbrace}} \frac{|S|!(p - |S| - 1)!}{p!} (val(S \cup \lbrace x_j \rbrace - val(S))

• $\phi_{j}$: 特徴量jのシャープレイ値
• $val$: 値関数（後述）
• $S$: モデルで使用されている特徴量の部分集合
• $p$: 特徴量の数

$val_x(S)$は集合$S$に含まれていない特徴量で周辺化された集合$S$の特徴量の値に対する予測です。

val_x(S) = \int \hat{f}(x_1, ... , x_p)d \mathbb P_{x \notin S} - E_X(\hat{f}(X))

$val(S \cup \lbrace x_j \rbrace - val(S))$のところから分かるように、特徴量jが加わった時の値関数の値と、特徴量jがなかった時の値関数との値との差分を特徴量jによる限界貢献度として計算し、それを$x_j$を含まない特徴量の部分集合$S$によって全ての組み合わせを計算、限界貢献度の平均をとる、という操作を行なっています。

このような計算によって求めるシャープレイ値を使って、SHAPでは説明を次のようにします。

g(z^{\prime}) = \phi_0 + \sum_{j=1}^{M} \phi_j z_j^{\prime}

• $g$: 説明モデル
• $z^{\prime}$: 連合ベクトル（要素が1の時、対応する特徴量が存在、0の場合不在を表すベクトル）
• $M$: 連合ベクトルの最大値
• $\phi_j$: 特徴量jのシャープレイ値

このように、SHAPではシャープレイ値による説明がLIMEで行なっていたような、特徴量の効果の総和として表現することができます。

値関数の実際の計算方法など、SHAPのアルゴリズムの詳細については、interpretable machine learning 5.10節を参照していただければと思います。

実装

実際に各手法を用いてモデルの局所的な説明を行います。
今回はタイタニックのデータセット、モデルにLightGBMを用いてそれぞれの手法を適用してみたいと思います。
いずれの手法についてもpythonで実装されたライブラリが公開されており、簡単に使用することができます。
（特徴量の説明はTitanic：タイタニック号乗客者の生存状況より引用)

特徴量の説明

pclass： 旅客クラス（1＝1等、2＝2等、3＝3等）
name： 乗客の名前
sex： 性別（male＝男性、female＝女性）
age： 年齢。一部の乳児は小数値
sibsp： タイタニック号に同乗している兄弟（Siblings）や配偶者（Spouses）の数
parch： タイタニック号に同乗している親（Parents）や子供（Children）の数
ticket： チケット番号
fare： 旅客運賃
cabin： 客室番号
embarked： 出港地（C＝Cherbourg：シェルブール、Q＝Queenstown：クイーンズタウン、S＝Southampton：サウサンプトン）
boat： 救命ボート番号
body： 遺体収容時の識別番号
home.dest： 自宅または目的地
survived：生存状況（0＝死亡、1＝生存）

explainer.py

import pandas as pd
import numpy as np
import lightgbm as lgb
import shap
import category_encoders as ce
from sklearn.model_selection import train_test_split
from lime.lime_tabular import LimeTabularExplainer
from alibi.explainers.anchor_tabular import AnchorTabular
from alibi.utils.data import gen_category_map

# csvファイル読み込み
train = pd.read_csv("../input/train.csv")
sample_submission = pd.read_csv("../input/gender_submission.csv")

# データ整形
label_enc_list = ["Sex", "Embarked"]
ce_oe = ce.OrdinalEncoder(cols=label_enc_lit,handle_unknown='impute')
train = ce_oe.fit_transform(train)
for column in label_enc_list:
    train[column] = train[column] - 1
train["Age"].fillna(train["Age"].median(), inplace=True)
train.drop(['PassengerId', 'Name', 'Cabin', 'Ticket'], axis=1, inplace=True)
X = train.drop(['Survived'], axis=1)
y = train['Survived']

# 学習
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
lgb_model = lgb.LGBMClassifier(objective='binary')
lgb_model.fit(X_train, y_train, eval_set = [(X_test, y_test)],
        categorical_feature=["Sex", "Embarked"], early_stopping_rounds=20,verbose=10)

# 説明したいインスタンスのindex
instance_index = 0 

##### LIME ######
# LIME,Anchorを使う場合モデルは確率値を返す必要がある
def predict_fn(x):
    prob = lgb_model.predict_proba(x, num_iteration=lgb_model.best_iteration_)
    return prob
# 離散値のカラムはcategorical_featuresに指定しないと連続値として扱われサンプリングされてしまう
lime_explainer = LimeTabularExplainer(
    training_data=X_train.values, feature_names=list(X_train.columns), class_names=["Not Survived", "Survived"],
    categorical_features=["Pclass", "Sex", "SibSp", "Parch", "Embarked"], verbose=True, mode="classification", random_state=42
)

result = lime_explainer.explain_instance(X_test.values[instance_index], predict_fn, num_features=10)
result.show_in_notebook(show_table=True)

##### Anchor #####
def predict_fn(x):
    prob = lgb_model.predict_proba(x, num_iteration=lgb_model.best_iteration_)
    return prob

anchor_explainer = AnchorTabular(
    predictor=predict_fn,
    feature_names=list(X_train.columns)
)
anchor_explainer.fit(X_train.values, disc_perc=[25, 50, 75])
anchor_explainer.explain(X_test.values[instance_index], threshold=0.95)

##### SHAP ######
shap.initjs()
explainer = shap.TreeExplainer(lgb_model)
shap_values = explainer.shap_values(X_train)
shap.force_plot(explainer.expected_value, shap_values[instance_index, :], X_test.iloc[instance_index, :], link="logit")

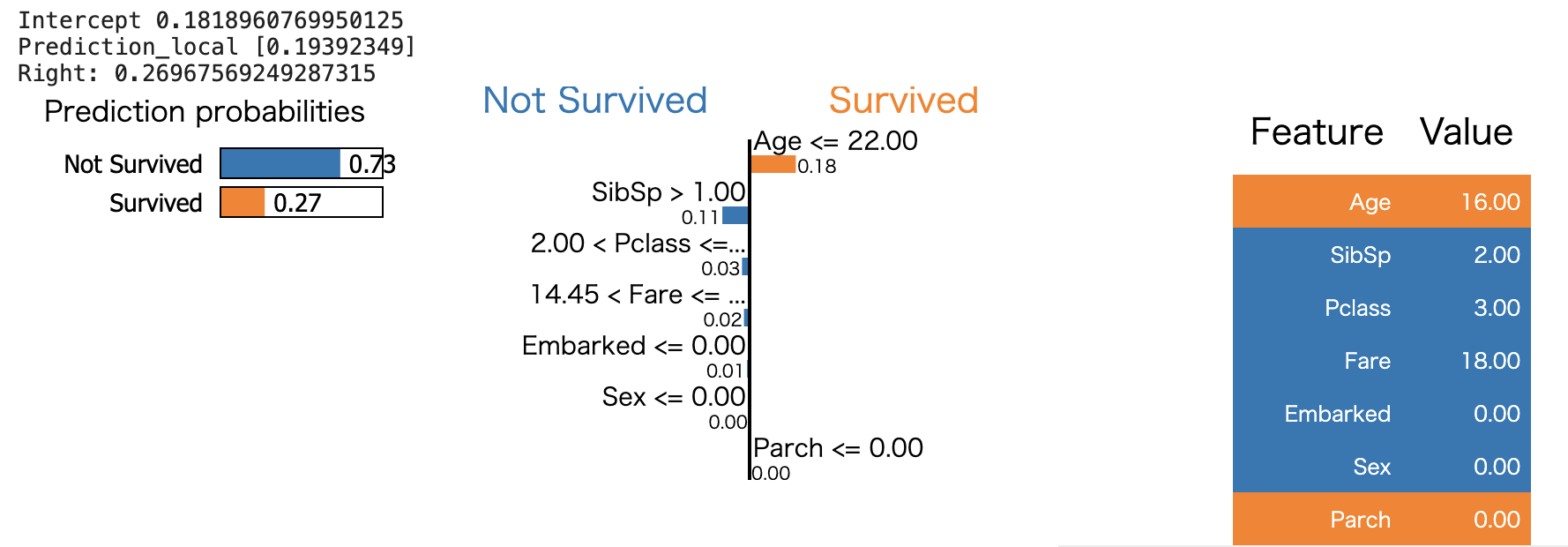
####LIMEを使った場合

図の見方としては、左のPrediction Probabilitiesがブラックボックスな機械学習モデルの出力値、Prediction_localが解釈可能なモデル（limeライブラリではデフォルトの設定でRidge回帰が用いられます）の出力値、真ん中の各特徴量ごとに表示されたグラフは各特徴量ごとの重み、右のFeature Valueがインスタンスの実際の特徴量の値となっています。

真ん中のグラフから、例えば年齢が22歳以下であることがSurvivedの確率を18%向上させていること、SibSp（タイタニック号に同乗している兄弟（Siblings）や配偶者（Spouses）の数）が1より大きいこと（このインスタンスではFeature Valueの表から兄弟、配偶者が2人）が生き残る確率を3%低下させていることが読み取れます。

このように、ブラックボックスなモデルに対してLIMEを使った場合、どの特徴量がどのくらい出力に寄与しているかを読み取ることができます。

####Anchorを使った場合
（今回使っているライブラリではLIME, SHAPのようにグラフ化して出してくれる訳ではありません）

見方としては、anchorが予測を"固定"するのに十分と判断された決定規則、precisionが精度、coverageがカバレッジの数値を示しています。このインスタンスのanchorを使った説明としては、性別が1（女性）で、Pclass（旅客クラス 1＝1等、2＝2等、3＝3等）が2等以下であることが、このインスタンスの乗客が生き残ると判断された規則となっており、精度が100%の確率で正確であり、カバレッジが17%であることがわかります。

決定規則として性別、旅客クラスの二つの特徴量が予測結果の主な原因であることが読み取れるので、ルールが解釈しやすいことが分かるかと思います。また、LIMEとの違いとして先ほど説明した「カバレッジ」があり、この値によって、どれほどこの決定規則が他のインスタンスに対して適用できるかを知ることができます。

例えば、決定境界周辺のインスタンスについては決定規則に用いられる特徴量が多く、カバレッジが低くなっており、決定規則がそのインスタンスに限定した説明になってしまっているだろう、と解釈することができます。
（あるインスタンスでは、'anchor': ['Sex > 0.00', 'Embarked > 0.00', 'Parch > 0.00', 'Age <= 22.00'], 'precision': 0.9640718562874252, 'coverage': 0.012841091492776886 となっており、カバレッジが1%程度と先ほどのインスタンスのカバレッジに比べ小さい値になっていました）

####SHAPを使った場合

SHAPではforce_plotを使うことでインスタンスごとの予測の説明を行うことが出来ます。
LIMEと同じように各特徴量ごとに予測値に対してどれだけ貢献しているか、という解釈が出来ますが、その値の解釈については注意が必要です。
各特徴量ごとの貢献度は、その特徴量がモデルの学習に含まれた時とそうでない時との予測値の差ではなく、全ての予測値の平均を基準値として、各特徴量が実際の予測値にどれだけ貢献したか、を表していると解釈されます。

上記の例であれば、基準値となる確率値が0.337で、この基準値から、このインスタンスの予測値である0.55に対して、年齢、性別、タイタニック号に同乗している親（Parents）や子供（Children）の数といった変数が生存確率を向上させ、旅客クラス、出港地が確率を低下させていると解釈できます。

#各手法の比較
LIME, Anchor, SHAPについて、それぞれの長所と短所を挙げていきたいと思います。

####LIME
長所として、LIMEでは解釈可能なモデルをブラックボックスなモデルに当てはめるので、当てはめたモデルの解釈の仕方をそのまま適用することができます。実装例ではRidge回帰を使いましたが、Lassoや決定木などを使うこともでき、モデルを柔軟に変更することができます。

短所として、近傍を定義することが難しいことにあります。カーネル幅を変えることで摂動空間のインスタンスの重みが変わり、モデルの学習結果も変わってしまうので、「適切な」カーネル幅を見つけてあげる必要がありますが、カーネル幅を探索する明確な目標がある訳ではなく、異なるカーネルの設定を試して、説明が意味をなしているか確認する他ありません。

####Anchor
LIMEと比較して複数の長所があります。まず1つには解釈がわかりやすい点です。先ほどのタイタニックの例でも、「性別が女性で旅客クラスが2等以下なので、機械学習モデルはこの乗客を生存すると予測した」というように言葉で説明がしやすいです。
また、LIMEでは解釈可能なモデルとして複雑性の低い線形モデルを当てはめますが、ブラックボックスなモデルの予測が非線形や複雑な場合だと局所的でも近似することが難しいケースがあります。そのようなケースでもAnchorであれば機能することが知られています。

短所として、LIMEで適切なカーネル幅を探索する必要があったように、Anchorでもビーム幅や精度の閾値などのハイパーパラメータを調整する必要があること、また多くの場合離散化しないとAnchorの定義を満たす摂動空間のインスタンスが見つからず結果が具体的すぎたりカバレッジが低くなり過ぎてしまいます。ただ離散化は不用意に使用すると決定境界が曖昧になる可能性があり、データをよくみながら離散化手法を適用してあげる必要があります。

####SHAP
長所として、SHAPで計算するシャープレイ値は予測と予測の平均との差分をインスタンスの特徴量間で公平に分配されます（LIMEの場合はこの性質は保証されません）
また、SHAPであれば局所的な説明だけでなく大域的な説明にも用いることができるため統一的な説明が可能です。
他の手法の場合は、局所的な説明にはLIME、大域的な説明には（今回は紹介していませんが）partial dependence plot, permutation feature importanceを用いるなど、局所的な説明、大域的な説明で別々の手法を使う必要が出てきてしまいます。大域的、局所的な説明の両方が求められるケースにおいては、SHAPを用いることが推奨されるかと思います。

まとめ

局所的な説明を行いたい時の各手法の使い分けですが、個人的な感覚としては、分かりやすい解釈が求められる時はAnchorが有用かと思います。ただAnchorでは各特徴量ごとの貢献度が分からないので、貢献度を調べたい場合SHAPを使う、といった使い分けになるかと考えています。LIMEは考え方が直感的で使いやすいのですが、Anchorに比べて重要度の指標になるようなものがなく、モデルの解釈の信憑性が保証できない点が特に実務では使いづらいかと思っています。

おわりに

今回はブラックボックスな機械学習モデルのインスタンスごとの解釈を可能にする手法として、LIME, Anchor, SHAPを取り上げ、それらの手法の概要、使い方について説明しました。　各手法ごとにどのような説明が行えるかが変わるので、クライアントがどのような説明を求めているかに応じて適切に使い分けながら、実務でも活用して頂ければと思います。

参考文献

• interpretable machine learning 日本語訳サイト
• Ribeiro, Marco Tulio, Sameer Singh, and Carlos Guestrin. "Why should I trust you?: Explaining the predictions of any classifier." > https://arxiv.org/pdf/1602.04938.pdf
• Marco Tulio Ribeiro, Sameer Singh, Carlos Guestrin. "Anchors: High-Precision Model-Agnostic Explanations." > https://ojs.aaai.org/index.php/AAAI/article/view/11491
• Lundberg, Scott M., and Su-In Lee. "A unified approach to interpreting model predictions." > https://arxiv.org/abs/1705.07874