概要
SVGの生成モデルDeepSVGを提案している論文を読んだので紹介してみます。
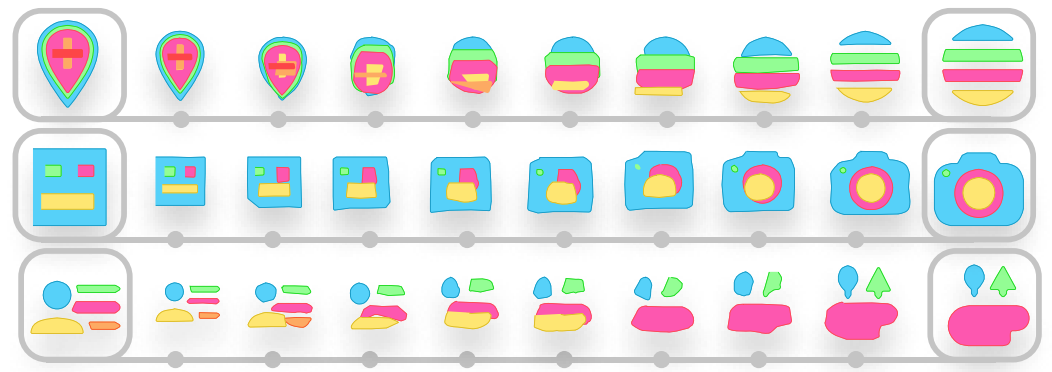
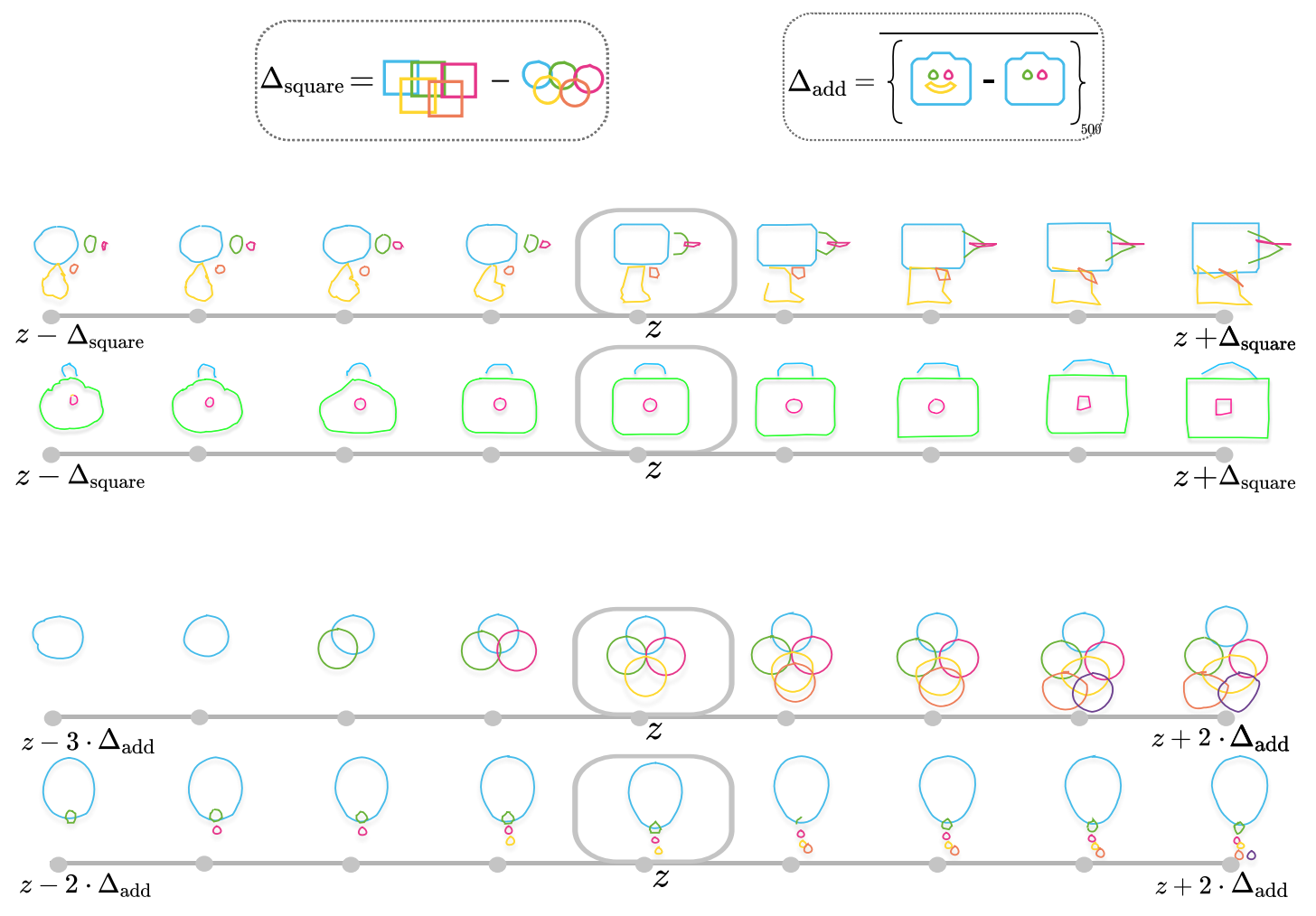
ラスタ画像に関する深層学習の生成モデルは様々に研究されていますが、ベクタ画像の生成モデルはそれほどには研究されているとは言えません。本論文が提案しているDeepSVGは、代表的なベクタ画像のひとつであるSVGをエンコード・デコードできるモデルです。このモデルによって、SVGの生成や補間、潜在変数を利用した図形の足し算や引き算ができるようになります。
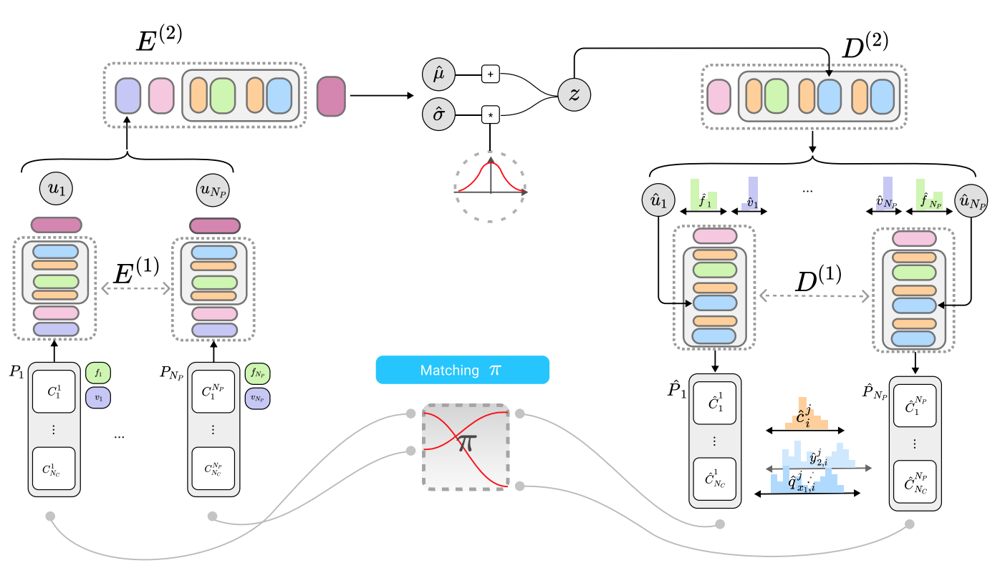
このモデルは、Transformerをベースとした2段階のEncoder/Decoderを持つVAEになっています。1段階目のEncoderは、 SVGに含まれる複数のパスをエンコードするのに使われ、2段階目のEncoderは、パスごとに得られた表現を集約し、潜在空間へとマッピングするのに使われます。Decoder側も同様の階層性を持っています。
また、本研究では、深層学習モデルだけでなく、新しいデータセットSVG-Icons8も提案しています。
この記事では、SVGのデータの表現方法、ネットワーク構造、損失関数について紹介します。
書誌情報
- Carlier, Alexandre, et al. "DeepSVG: A Hierarchical Generative Network for Vector Graphics Animation." arXiv preprint arXiv:2007.11301 (2020).
- https://arxiv.org/abs/2007.11301
- 公式実装(PyTorch)
- プロジェクトページ
SVGデータの表現方法
まず、SVGデータの表現方法についてみていきます。まず、本研究で用いるSVGのコマンドについて確認し、次に、SVG内のパスに付与されるプロパティを確認します。最後に、SVGの埋め込み表現について確認します。
SVGのコマンド
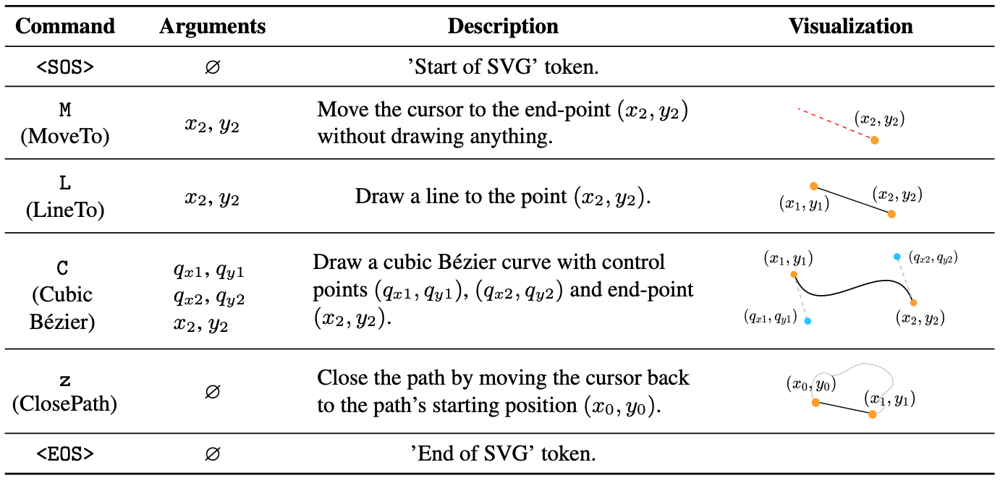
通常、SVG画像は複数のパスから構成されています。これらのパスはいくつかの単純な描画コマンドの組み合わせでできています。コマンドには引数が必要で、それによって描かれる線の性質が変化します。
本研究では、SVG内のパスを以下のコマンドと引数で表現します。
SOS, EOSは引数の存在しないコマンドで、パスの開始と終了を表します。また、$z$も引数の存在しないコマンドで、パスの始点と終点を接続して閉じたパスを作成するというコマンドです。M,L,CはそれぞれMoveTo, LineTo, CubicBézierを表します。
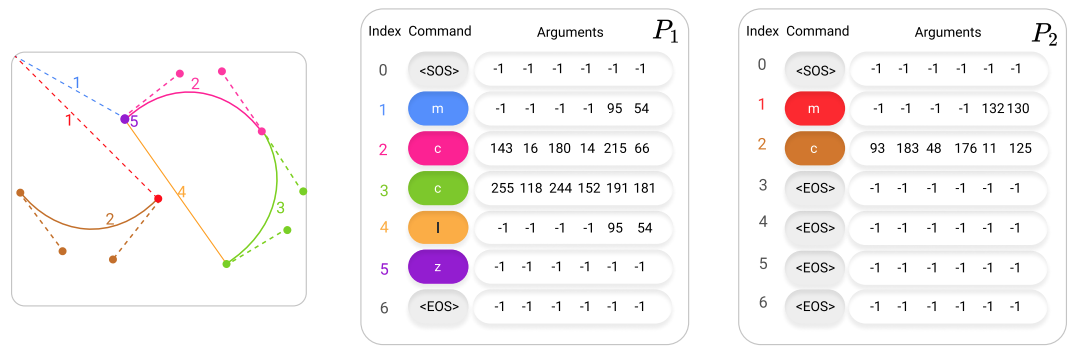
これらのコマンド、引数を用いると、例えば下図のようなパスを描くことができます。コマンドの引数は最大で6個ですが、対応する引数がない場合は-1で埋められます。以下の例だと、最大で$N_c=7$のコマンド数を想定しており、それに足りない場合は、EOSコマンドでパディングします。
なお、実際のSVGの仕様には、例えばElliptical Arcのようなコマンドもあり、上記のコマンドのみでは対応できないケースもあるため、先ほどの6つのコマンドで代替したり、近似したりする必要があります。また、前処理として、他のSVG画像とスケールを揃えたり、コマンドを削減/補間したり、座標を相対座標から絶対座標に変換したり、といった正規化が必要になります。この辺りの処理は、Appendixに詳細が記載されていますのでご興味のある方は参照してください。
パスのプロパティ
パスには、複数のコマンドと引数の他に、塗り潰しを表す$f \in \{0,1,2\}$というプロパティ、パスの可視/不可視を表現する$v \in \{0,1\}$というプロパティが付与されます。
塗り潰しを表すプロパティがとりうる3つの値は、それぞれ、outline/fill/eraseを表します。outlineはパスの輪郭だけを残し、fillは閉じたパス内を黒く塗り潰し、逆にeraseは閉じたパス内を白に塗り潰します。
ベクタ画像は複数のパスによって構成されていますが、画像によって必要なパス数は、当然異なります。本手法ではパスの数を$N_P$に固定し、足りていないパス数はパディングされます。$v$は、このようなパディングを表現するのに使用されます。
SVGの埋め込み表現
SVG内のコマンドとそれに与えられる引数は、ネットワークに入力するにあたり埋め込み表現に変換する必要があります。
コマンド、引数の座標、コマンドの順番(インデックス)のそれぞれから埋め込み表現が得られ、それらを足し合わせて、$i$番目パスの$j$番目のコマンドと引数は$e_i^j \in \mathbb{R}^{d_E}$という埋め込み表現に変換されます。
e_{i}^{j}=e_{\mathrm{cmd}, i}^{j}+e_{\mathrm{coord}, i}^{j}+e_{\mathrm{ind}, i}^{j}
コマンドの埋め込み表現
6種類のコマンドの埋め込み表現は、そのコマンドを表すone-hotベクトル$\delta_{c_{i}^{j}} \in \mathbb{R}^6$と、行列$W_{\mathrm{cmd}} \in \mathbb{R}^{d_E \times 6}$によって、以下のように得られます。
e_{\mathrm{cmd}, i}^{j}=W_{\mathrm{cmd}} \delta_{c_{i}^{j}}
座標の埋め込み表現
コマンドに与えられる引数は、-1と0~255の整数によって表現されています。-1は引数が不要な場合に埋め合わせるための値で、その他は座標を表す値です。座標を表す値は、0~255の整数に量子化されており、つまりはカテゴリカル変数として扱われます。
1つのコマンドあたり6つの引数が存在しており、それぞれをone-hot表現で表して結合すると、コマンドに対する引数$X_i^j$のサイズは$\mathbb{R}^{257 \times 6}$となります。257は、0~255の整数(256次元)に、-1(1次元)を加えた次元数です。
6つの引数はそれぞれ個別に$W_X \in \mathbb{R}^{d_E \times 257}$によって埋め込まれ、$W_{\text {coord }} \in \mathbb{R}^{d_E \times 6d_E}$によってさらに$d_E$次元の埋め込み空間へと写像されます。
e_{\text {coord }, i}^{j}=W_{\text {coord }} \operatorname{vec}\left(W_{X} X_{i}^{j}\right)
インデックスの埋め込み表現
本手法のネットワークはTransformerをベースにした構造を採用しています。Transformerでは、入力トークンの位置を表すPositionalEncodingという埋め込み表現が使われますが、本手法でもこれに対応するインデックスの埋め込み表現が使用されます。
パス内において、コマンドが$j$番目に位置しているという情報を表現するために、$j$番目の要素のone-hot表現である$\delta_j \in \mathbb{R}^{N_C}$と行列$W_{\mathrm{ind}} \in \mathbb{R}^{d_{E} \times N_C}$を用いて、$e_{\mathrm{ind}, i}^{j} \in \mathbb{R}^{d_E}$が得られます。
e_{\mathrm{ind}, i}^{j}=W_{\mathrm{ind}} \delta_{j}
パス数とコマンド数
本手法では、ひとつのSVG画像に含まれるパス数$N_P$と、ひとつのパスに含まれるコマンド数$N_C$は固定の値が用いられています。パス数が$N_P$に満たない場合は、EOSのみからなるパスがパディングされ、そのプロパティ$v$は不可視に設定されます。また、各パスに含まれるコマンド数が$N_C$に満たない場合は、EOSコマンドによってパディングされます。
ネットワーク構造
以下に本手法のネットワーク構造を示します。大きく見れば、VAEになっており、Encoder/Decoderはいずれも2段階のTransformerベースの構造になっています。Encoder/Decoderの1段階目では、ひとつひとつのパスが独立してエンコード/デコードされ、2段階目は全パスのエンコード/デコードを行っています。
エンコーダー
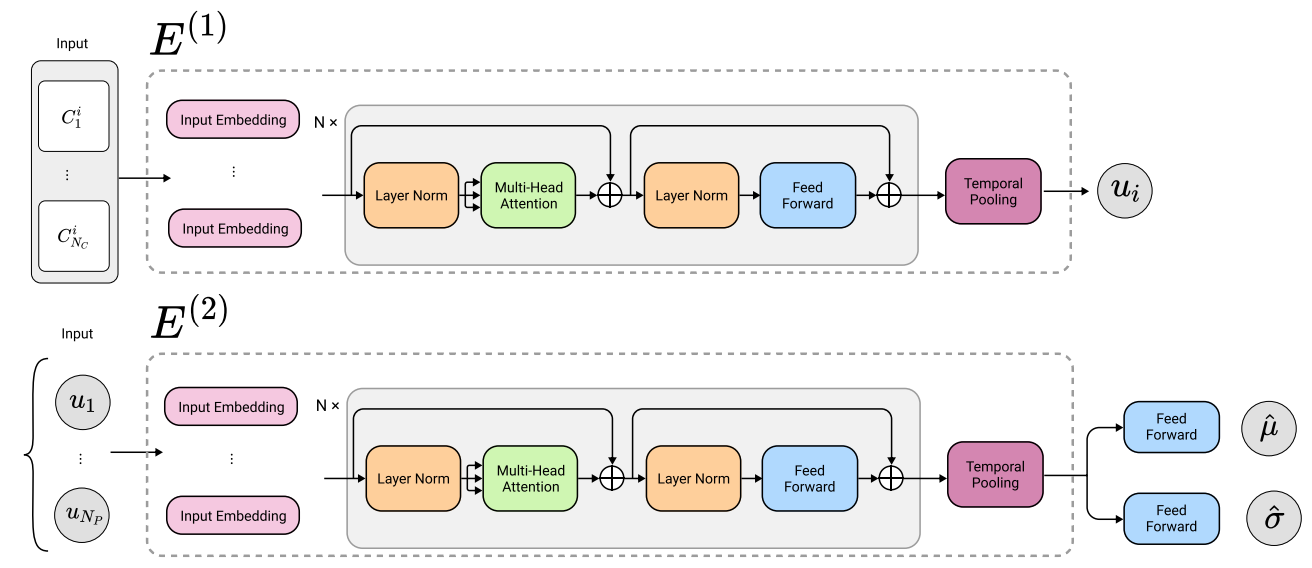
まずは個々のパスが独立してエンコードされます。$i$番目のパスは、埋め込み表現に変換された後$E^{(1)}$に入力され、EOSコマンドによるパディング部分を除いたTemporalPoolingによって平均されることで、対応する出力$u_i$が得られます。
同様に、$\{u_i\}_1^{N_P}$系列が$E^{(2)}$に入力され、不可視の領域を除いてTemporalPoolingされることで、SVG画像全体の潜在表現が得られます。
この潜在表現を元に、1層のLinear層によって$\hat{\mu}, \log\hat{\sigma}$が得られます。通常のVAEと同様に、これらを用いた分布からサンプルされた$z$を使って以降の処理を進めるという、reparameterization trickが使用されます。
以下、補足というか疑問点です。パスには塗り潰しを表す$f_i$や可視/不可視を表す$v_i$というプロパティがあるはずですが、上の図ではそれらに関する情報が出現していません。$v_i$は$E^{(2)}$のTemporalPoolingで使用するので良いのですが、$f_i$に関してはどこでも使用されていないように見えます。公式実装も小一時間眺めてみたのですが、ついに疑問は解けませんでした。$f_i$はパスごとに設定されている値なので、$E^{(2)}$に入力される$u_i$に混ぜてEmbeddingを作っているのかなあと予想していますが、定かではありません。$E^{(2)}$にはPositionalEncodingに関する記載もないので、この辺りの記述が現在のバージョンの論文では抜け落ちているのかもしれません。
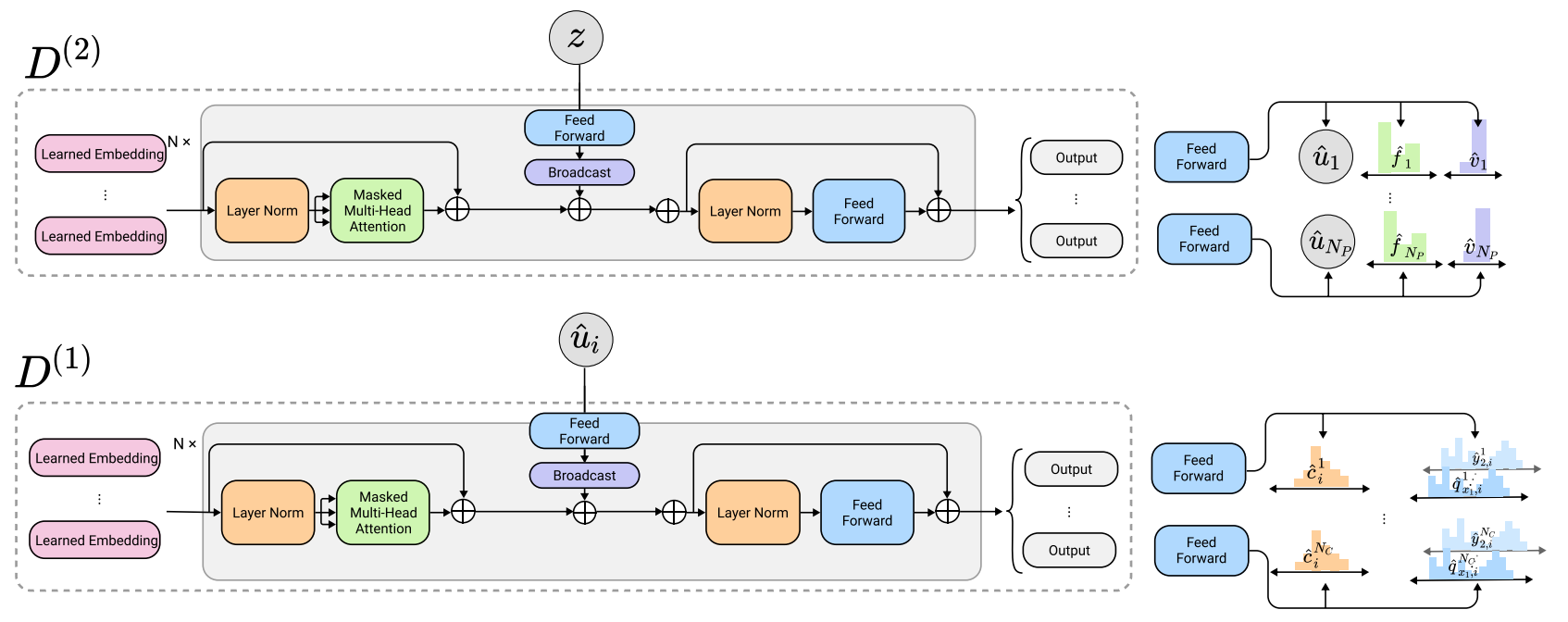
デコーダー
デコーダー側では、$D^{(2)}$によって、$z$を元に$\{ \hat{u}_i \}_ 1^{N_P}$系列と各パスのプロパティの推定結果 $\{ \hat{f}_i, \hat{v}_i \}_1^{N_P} $が出力されます。これらは独立に$D^{(1)}$に入力され、コマンドと引数が推定されます。
以下は、デコーダーの詳細です。通常のTransformerのデコーダーと同様に、Masked Multi-Head Attentionが使用され、生成対象より先の位置にある入力にはAttentionが向けられないようにしています。
損失関数
最後に、損失関数について確認しましょう。基本はVAEですので、$z$の分布が$\mathcal{N}(0, I)$から離れてはいけないというKL距離による損失と、入力と出力が同じになる再構成誤差損失とから成り立っています。入力は全てカテゴリカル変数ですので、損失は全て分類損失となっており、以降の数式中に現れる$\ell$はいずれもクロスエントロピー損失を表しています。損失は非可視のパスやパディングされているコマンドに対応する部分には適用されません。
なお、$i$は入力側のパスのインデックスを、$\hat{\imath}$は出力側のパスのインデックスを表します。
L_{\hat{\imath}, i}(\theta)=w_{\mathrm{vis}} \ell\left(v_{\hat{\imath}}, \hat{v}_{i}\right)+v_{i} \cdot\left(w_{\mathrm{fill}} \ell\left(f_{\hat{\imath}}, \hat{f}_{i}\right)+\sum_{j=1}^{N_{C}}\left(w_{\mathrm{cmd}} \ell\left(c_{\hat{\imath}}^{j}, \hat{c}_{i}^{j}\right)+w_{\mathrm{args}} l_{\mathrm{args}, \hat{\imath}, i}^{j}\right)\right)
l_{\mathrm{args}, \hat{\imath}, i}^{j}=\mathbf{1}_{c_{i}^{j} \in\{\mathrm{m}, 1, \mathrm{c}\}}\left(\ell\left(x_{2, \hat{\imath}}^{j}, \hat{x}_{2, i}^{j}\right)+\ell\left(y_{2, \hat{\imath}}^{j}, \hat{y}_{2, i}^{j}\right)\right)+\mathbf{1}_{c_{i}^{j}=\mathrm{c}} \sum_{k \in\{1,2\}} \ell\left(q_{x_{k}, \hat{\imath}}^{j}, \hat{q}_{x_{k}, i}^{j}\right)+\ell\left(q_{y_{k}, \hat{\imath}}^{j}, \hat{q}_{y_{k}, i}^{j}\right)
ここで、$i, \hat{\imath}$の対応関係というのが問題になります。SVG中のパスはどのような順番でも良いので、入力されたパスの順番と出力されたパスの順番が合致しているという保証はありません。
そのため、パス同士の対応づけをどのようにするのかという戦略が必要になります。本論文では2つの戦略を比較しています。1つ目はOrdered戦略で、何らかの基準を設けて整序するという戦略です。各パスの開始地点(パスのなかの開始地点になりうる点の中で最も左上の点)の辞書順序を使用しています。2つ目はHungarian戦略で、損失を全通り計算してみた後にハンガリアンアルゴリズムによって損失が最小になる組み合わせを発見する、という戦略です。
何人かの被験者にって実験した結果、1つ目の方法であるOrdered戦略が良い結果になると評価されています。以下に、Ordered戦略を採用した時の損失関数を示します。
L(\theta)=w_{\mathrm{KL}} \mathrm{KL}\left(p_{\theta}(z) \| \mathcal{N}(0, I)\right)+\sum_{\hat{\imath}=1}^{N_{P}} L_{\hat{\imath}, \pi_{\mathrm{ord}}(\hat{\imath})}(\theta)
まとめ
以上、DeepSVGと呼ばれるSVGに関する生成モデルの論文を紹介しました。基本はVAEなので、VAEでできそうな様々なアプリケーションが実現できるということが論文のAPPENDIXやプロジェクトページで確認できます。
マッチングの戦略については、ある程度までOrderedで訓練した後、Hungarianに切り替えて訓練するとより良い結果になったりするかも、と思ったりしました。