概要
CVPR2020のベストペーパーに輝いた論文を読んでみたので紹介します。
本研究は、単一の静止画から3次元形状を復元するという手法です。興味深いのが、いかなるアノテーションや形状に関する事前知識をつかわずに訓練するという「in the Wild」な手法であるということです。
デモページが公開されているので、まずは動かしてみることをお勧めします。
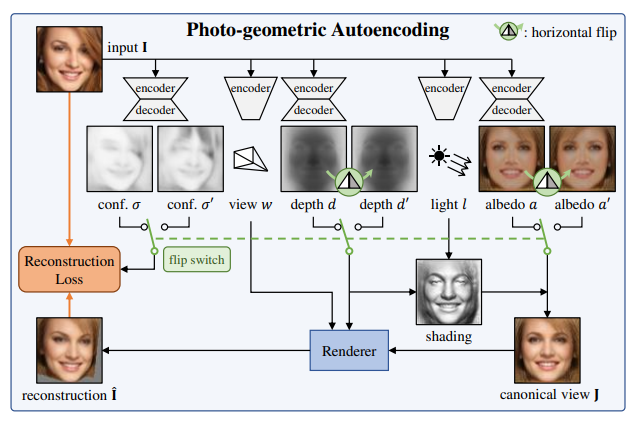
この手法では、RGB入力画像と同じ画像を出力するというAutoEncoder風の構造を持ったネットワークを使用します。この内部では、以下の4つの要素を明示的に推定しています。
- アルベド: $a \in \mathbb{R}^{3 \times W \times H}$
- 深度: $d \in \mathbb{R}_{+}^{W \times H}$
- 照明: $l \in \mathbb{S}^{2}$
- 視点: $w \in \mathbb{R}^{6}$
そして、この4つの要素を使ってレンダリングを行い2次元RGB画像を出力します。レンダリングには、いわゆる微分可能レンダラーが使用されていますので、入力画像と出力画像の差異をもとに算出した損失をもとに、ネットワーク全体を訓練することが可能です。
しかし、これらの要素を単一の静止画から推定するというのは、不良設定問題です。そこで、本手法では対象の物体が左右対称であるという仮定を置いています。この仮定をおくと、アルベドや深度のみを反転させた状態でレンダリングを行っても、同じ出力結果になるべき、という新しい制約条件が得られます。
一方で、このような左右対称という制約は強すぎる制約です。例えば、人の顔であればヘアスタイルなどによって完全な左右対称は実現できません。そこで、本当にこの領域は左右対称なのかという信頼度も別途推定し、損失はその信頼度も考慮に入れて算出します。
以上の流れをまとめたのが論文中の図2になります。
記事内では、もう少し細かい部分を見ていきます。
書誌情報
- Wu, Shangzhe, Christian Rupprecht, and Andrea Vedaldi. "Unsupervised Learning of Probably Symmetric Deformable 3D Objects from Images in the Wild." Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2020.
- プロジェクトページ
- デモページ
- 公式実装(PyTroch)
損失関数
いきなりですが、簡単なのでまずは損失関数から確認してきましょう。
基本的には、入力画像と出力画像が似るようにしたい、という再構成損失だけです。
再構成損失は、以下のように算出されます。$\sigma_{uv}$は座標$(u,v)$の対称性の不確かさを表し、0に近いほど対称性が信頼でき、大きくなればなるほど信頼できないということを表します。
\mathcal{L}(\hat{\mathbf{I}}, \mathbf{I}, \sigma)=-\frac{1}{|\Omega|} \sum_{u v \in \Omega} \ln \left( \frac{1}{\sqrt{2} \sigma_{u v}} \exp -\frac{\sqrt{2} \left|\hat{\mathbf{I}}_{u v}-\mathbf{I}_{u v}\right|}{\sigma_{u v}} \right)
この数式の$\ln$の中は、中心が0、分散が$\sigma^2_{uv}$のラプラス分布となっています。なので、$\left|\hat{\mathbf{I}}_{u v}-\mathbf{I}_{u v}\right| = 0$が最も好ましいが、$\sigma_{uv}$が大きければ大きいほど多少外れても仕方ないねという損失になります。
本手法では、再構成誤差としていわゆるperceptual損失を加えています。VGG16のrelu3_3の出力を用いて、その差異をもとに以下のような損失を定めています。
\mathcal{L}_{\mathrm{p}}^{(k)}\left(\hat{\mathbf{I}}, \mathbf{I}, \sigma^{(k)}\right)=-\frac{1}{\left|\Omega_{k}\right|} \sum_{u v \in \Omega_{k}} \ln \left(\frac{1}{\sqrt{2 \pi\left(\sigma_{u v}^{(k)}\right)^{2}}} \exp -\frac{\left(\left|e_{u v}^{(k)}(\hat{\mathbf{I}})-e_{u v}^{(k)}(\mathbf{I})\right|\right)^{2}}{2\left(\sigma_{u v}^{(k)}\right)^{2}}\right)
$e_{u v}^{(k)}$はVGG16のrelu3_3を表します。また、こちらはラプラス分布ではなく、ガウス分布を想定した損失になっています。また、$\sigma^{(k)}$は先ほどの$\sigma$をそのまま流用してもよさそうですが、別途改めて推定するようです。
冒頭に述べたように、アルベドや深度画像を反転させた状態でも推論させてみて、そちらでも損失を計算します。対称性の不確かさを表す$\sigma_{u v}$だけは、反転はできないので、別途推定する必要があります。これらを、$a', d', \sigma^{\prime}, \sigma^{\prime(k)}$、出力される画像を$\hat{\mathbf{I}^{\prime}}$とすると、最終的な損失は以下のように計算されます。$\lambda_k = 0.5$は左右反転時の損失の重みづけです。
\left(\mathcal{L}(\hat{\mathbf{I}}, \mathbf{I}, \sigma) + \mathcal{L}_{\mathrm{p}}^{(k)}\left(\hat{\mathbf{I}}, \mathbf{I}, \sigma^{(k)}\right)\right) + \lambda_f\left(\mathcal{L}(\hat{\mathbf{I}'}, \mathbf{I}, \sigma') + \mathcal{L}_{\mathrm{p}}^{(k)}\left(\hat{\mathbf{I}'}, \mathbf{I}, \sigma^{\prime(k)}\right)\right)
レンダリング処理
入力画像から$a, d, l, w$といった要素を推定するのは、CNNベースの典型的なEocoderやDecoderによってなんとなくできそうですが、これらの要素をつかってレンダリングする部分は、やや複雑です。大きく分けて2つの操作$\Pi, \Lambda$を通して、以下のように再構成画像$\hat{\mathbf{I}}$が得られます。
$$
\hat{\mathbf{I}}=\Pi(\Lambda(a, d, l), d, w)
$$
$\Lambda$は照明処理、$\Pi$は再投影の処理に該当します。
以下、投影モデルについて説明してから、照明処理と再投影処理について深堀していきます。
投影モデル
透視投影モデルを前提とします。
カメラの内部パラメータ$K$とすると、3次元空間における点$P$は、$p$に投影されます。ここで、内部パラメータ$K$は決め打ちしていて、視野角$\theta_{\mathrm{FOV}}$は$10^\circ$としています。
p \propto K P, \quad K=\left[\begin{array}{ccc}
f & 0 & c_{u} \\
0 & f & c_{v} \\
0 & 0 & 1
\end{array}\right], \quad\left\{\begin{array}{l}
c_{u}=\frac{W-1}{2} \\
c_{v}=\frac{H-1}{2} \\
f=\frac{W-1}{2 \tan \frac{\theta_{\mathrm{FOV}}}{2}}
\end{array}\right.
これを用いることで、下式のように深度画像上の点が3次元的にどのような点からに対応するのかを求めることができます。
$$
P=d_{u v} \cdot K^{-1} p
$$
照明処理
それでは、本題である照明処理と再投影処理の話に移ります。
照明処理$\Lambda(a, d, l)$では、まず、$d$と$l$とを用いることでシェーディングを得ます。シェーディングとアルベドを組み合わせると、その照明条件$l$で真正面から見たときにどのように見えるのかを表す正規化画像$\mathbf{J}$を得ます。この画像$\mathbf{J}$は、3次元モデルに貼り付けるテクスチャ画像といえます。
シェーディングの求め方
シェーディングはランバート反射モデルもとに算出されます。基本的には以下の手順で求めることができます。
- 深度画像$d$から法線マップ$n$を求める。
- 透視投影モデルを前提とし、深度画像から3次元点に変換する。
- 近隣点から構成される面の法線ベクトルをもとめ、それらを集めて法線マップを求める。
- 法線マップと照明$l$をかけ合わせ、シェーディングを得る
法線マップの求め方
「近隣点から構成される面の法線ベクトル」は、$x$方向と$y$方向で個別にベクトルを算出し、そのベクトルが成す平面に対する法線ベクトルを求めることで得られます。
以下の式の$e_{x}, e_{y}$はそれぞれ$x,y$方向の単位ベクトルです。
$$
t_{u v}^{u}=d_{u+1, v} \cdot K^{-1}\left(p+e_{x}\right)-d_{u-1, v} \cdot K^{-1}\left(p-e_{x}\right)
$$
$$
t_{u v}^{v}=d_{u, v+1} \cdot K^{-1}\left(p+e_{y}\right)-d_{u, v-1} \cdot K^{-1}\left(p-e_{y}\right)
$$
2つのベクトルが成す平面の法線ベクトルは、以下のように外積によって求められます。
$$
n_{u v} \propto t_{u v}^{u} \times t_{u v}^{v}
$$
ランバート反射
ランバート反射モデルに基づいて、照明を表すベクトル$l$と法線ベクトル$n$の内積によって求められます。照明$l$は、モデルが出力する$-1 \leq l_x, l_y \leq 1$を用いて、以下のように計算されます。
l=\left(l_{x}, l_{y}, 1\right)^{T} /\left(l_{x}^{2}+l_{y}^{2}+1\right)^{0.5}
正規化画像
このようにして得られたシェーディングを用いて、最終的には以下のような数式で正規化画像$\mathbf{J}_{u v}$が得られます。$k_s, k_d$は環境光の強さと拡散光の強さを表す係数で、これは入力画像から$l_x, l_y$と一緒に推定されます。
\mathbf{J}_{u v}=\left(k_{s}+k_{d} \max \left\{0,\left\langle l, n_{u v}\right\rangle\right\}\right) \cdot a_{u v}
再投影処理
再投影処理$\Pi(\mathbf{J}, d, w)$では、出力画像$\hat{\mathbf{I}}$の各座標$(u^{\prime} v^{\prime})$の画素値が正規化画像$\mathbf{J}$のどの画素から採られるのかということを求めます。
まず、画素の対応関係$\eta_{d, w}:(u, v) \mapsto\left(u^{\prime}, v^{\prime}\right)$を考えましょう。投影モデルを用いて、カメラの姿勢($w = (R, T)$)が加わったときに正規化画像のピクセル$p=(u, v, 1)$がどこに移動するのかが下式のように求められます。$p^{\prime}=\left(u^{\prime}, v^{\prime}, 1\right)$は再構成画像における座標です。
$$
p^{\prime} \propto K\left(d_{u v} \cdot R K^{-1} p+T\right)
$$
さて、この対応関係を用いれば別視点からの物体を描画できるようにも思いますが、オクルージョンの発生のためになかなか複雑な処理が必要になります。そのため、単純に上記の式をひっくり返して逆変換を求め、一般的なSpatial transformer networks(STN)1の枠組みでサンプリンググリッドを作成してBilinearSamplingを行うだけでは不十分です。当然、損失をもとにbackwardすることを考えると、forwardだけできればいいや、というわけにも行きません。
この問題を解決するために、本研究では、微分可能なレンダラーであるNeural Mesh Renderer(NMR)2を使用しています。本手法では、深度$d$を別視点$w$から見たときの深度$\bar{d}$をNMRによって得たのち、それを用いて以下のように逆の対応関係$\eta^{-1}_{\bar{d}, w}:(u', v') \mapsto\left(u, v\right)$を求めます。
$$
p \propto K\left(\bar{d}_{u' v'} \cdot R^{-1} (K^{-1} p^{\prime}-T)\right)
$$
これ以降の処理は、STNの枠組みで進めることができます。
まとめ
以上、簡単にですが、"Unsupervised Learning of Probably Symmetric Deformable 3D Objects from Images in the Wild"を読んで理解したことをまとめてみました。
いかなる追加情報もなしに、RGB画像のみから3次元形状が復元できるモデルが作れてしまう、というのは大変な驚きです。同一のカテゴリで、対称性を持っているものに限るという制約や、ランバート反射モデルを大きく逸脱している画像は対象外であるといった制約はあるものの、いろいろと遊べそうな手法です。