概要
事前に学習された画像生成モデルを蒸留することで、形状(コンテンツ)と外観(スタイル)を個別にコントロールできるような潜在空間を持つ新しい生成モデルを作る手法NeuralCrossbreedの論文を読んでみたので、紹介します。
下図は本手法で生成される画像群を表しています。上段は入力画像で、下段はそれを元に生成される画像群を表しています。2つの画像の間には、ひし形状に何枚もの画像が並べられていますが、2つの入力画像の形状と外観とが独立に補間された生成画像になっていることが確認できます。
よくあるモーフィング手法では、2つの画像間の対応するキーポイントを人が指定したり別の手法によって推定し、ワープ関数を最適化するという処理が必要ですが、本手法では深層学習モデルの推論処理によってこれらの処理をこなすので、単純に推論時間が短くなります。
書誌情報
- Park, Sanghun, Kwanggyoon Seo, and Junyong Noh. "Neural Crossbreed: Neural Based Image Metamorphosis." arXiv preprint arXiv:2009.00905 (2020).
- https://arxiv.org/abs/2009.00905
蒸留の枠組み
最初に、既存の生成モデルを蒸留して新しい生成モデルを作る、という枠組みについて説明します。一般的な蒸留の枠組みと同様に、既存の生成モデルは教師モデル、新しい生成モデルは生徒モデルと呼ばれます。
生徒モデルの訓練に使用するデータの作成
生徒モデルの訓練に使用されるデータは、教師モデルであるBigGANから生成される画像のtriplet$(x_A, x_B, x_\alpha)$および、画像$x_A, x_B$に対応するラベル$l_A, l_B$です。
BigGANでは、生成する画像のラベルを指定する必要がありますので、そのラベルを$l_A, l_B$とし、そのembeddingを$e_A, e_B$とします。一方で、2つの画像を生成するにあたってランダムにサンプルされた潜在変数を$z_A, z_B$とします。これらをBigGANに入力すると、画像$x_A, x_B$が生成されます。また、潜在変数とembeddingを線形補間した画像$x_\alpha$も生成されます。
\begin{array}{l}
x_{A}=\operatorname{BigGAN}\left(z_{A}, e_{A}\right), x_{B}=\operatorname{BigGAN}\left(z_{B}, e_{B}\right) \\
\left.x_{\alpha}=\operatorname{BigGAN}\left((1-\alpha) z_{A}+\alpha z_{B},(1-\alpha) e_{A}+\alpha e_{B}\right)\right)
\end{array}
以降は、$x_A$を、形状がAで外観がAの画像ということで$x_{AA}$、$x_B$を、形状がBで外観がBの画像ということで$x_{BB}$と表記します。同様に、それらの補間である$x_\alpha$は$x_{\alpha\alpha}$と表記します。
生徒モデルの構造
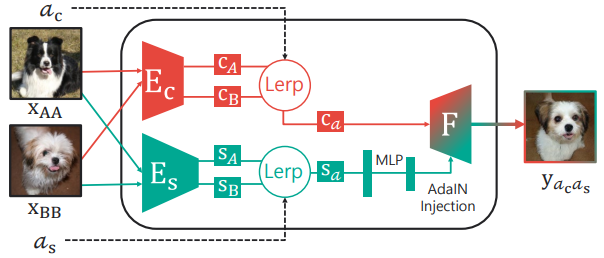
生徒モデルは以下のような構造になっており、2種類のエンコーダー$E_C, E_S$とDecoder$F$からなっています。訓練時には、教師モデルからサンプルされた画像が入力されますが、推論時はその限りではありません。
$E_C$は画像に含まれる物体の形状コード$C$を抽出し、$E_S$は画像に含まれる外観コード$S$を抽出します。2つの画像$x_{AA}, x_{BB}$についてこれらは個別に計算され、$C_A, C_B, S_A, S_B$が得られます。Lerpと記載されている線形補間の操作により、これらのコードは混合され、$C_{a_c} = a_cC_A + (1-a_c)C_B$と$a_sS_A + (1-a_s)S_B$が得られます。$F$と記載されている最終工程は、Adaptive Instance Normalization(AdaIN)を持つDecoderです。外観コードはMLPによって加工された後、AdaINの入力に使用されます。
このようにして、2つの画像の形状と外観とが個別に重み付けされた新しい画像$y_{a_ca_s}$が得られます。
生徒モデルの訓練
生徒モデルの訓練のためには様々な損失関数が適用されますが、Discirminatorによって与えられる敵対的損失と、生成された画像が期待する結果になっているかを表すPixel損失の2種類の損失を、様々な$(a_c, a_s)$の組み合わせに対して計算することで得られます。
敵対的損失は、Dsicriminatorによって与えられます。Discirminatorは、入力画像が教師モデルで生成されたか、生徒モデルで生成されたかを見抜けるように訓練されます。Multi Task Discriminatorになっており、教師モデルの生成画像$x$の生成時に指定したラベル$l$について、真偽を見極めます。そのため、敵対的損失は、特定のラベルとしてみたときの画像の外観の品質を評価している、と見なすことができます。生徒モデルの生成画像$y$は、異なるラベルの中間的な外観をしていることも多いのですが、そのようなケースについては後ほど確認します。数式的には、敵対的損失は以下のように表されます。
L_{a d v}(x, y, l)=\mathbb{E}_{x}[\log D(x \mid l)]+\mathbb{E}_{y}[\log (1-D(y \mid l))]
一方、Pixel損失は、期待する出力画像が明確にあるときに、生成画像がその期待する画像にどれだけ近いかをL1誤差によって評価したものです。
\|x-y\|_{1} \triangleq \mathbb{E}_{x, y}\left[\|x-y\|_{1}\right]
本手法では、これらの基本的な損失関数をいくつかの状況で適用することで全体の損失関数を構成しています。
Identity Loss
以下のようなケースでは、生徒モデルは元の入力画像$x_{AA}, x_{BB}$にかなり近い画像を出力することが期待されます。そのため、敵対的損失に加えて、Pixel損失が適用されます。
- $(a_c, a_s) = (0, 0)$のときの出力画像$y_{AA}$は、$x_{AA}$に近い画像になる。
- $(a_c, a_s) = (1, 1)$のときの出力画像$y_{BB}$は、$x_{BB}$に近い画像になる。
\begin{aligned}
L_{a d v}^{i d t} &=L_{a d v}\left(x_{A A}, y_{A A}, l_{A}\right)+L_{a d v}\left(x_{B B}, y_{B B}, l_{B}\right) \\
L_{p i x}^{i d t} &=\left\|x_{A A}-y_{A A}\right\|_{1}+\left\|x_{B B}-y_{B B}\right\|_{1} \\
\text { where } y_{A A} &=F\left(E_{c}\left(x_{A A}\right), E_{s}\left(x_{A A}\right)\right)=G\left(x_{A A}, x_{B B}, 0,0\right) \\
y_{B B} &=F\left(E_{c}\left(x_{B B}\right), E_{s}\left(x_{B B}\right)\right)=G\left(x_{A A}, x_{B B}, 1,1\right)
\end{aligned}
Morphing Loss
BigGANでは、embeddingと潜在変数を線形補間することで、$x_{AA}, x_{BB}$の補間画像といえるモーフィング結果$x_{\alpha\alpha}$を得ることができるのでした。このモーフィングは、訓練しようとしている生徒モデルと異なり、形状と外観を個別にコントロールすることはできませんが、生徒モデルの訓練に活用することができます。
- $(a_c, a_s)=(\alpha, \alpha)$のときの出力画像$y_{\alpha\alpha}$は、BigGANによるモーフィング結果$x_{\alpha\alpha}$に近い画像になる。
$y_{\alpha\alpha}$は2つのラベル$l_A, l_B$の中間的な外観を有しています。そのため、外観の品質を表す敵対的損失は、2つのラベルに対する敵対的損失の重み付き和として表現されます。
\begin{aligned} L_{a d v}^{m r p} &=(1-\alpha) L_{a d v}\left(x_{A A}, y_{\alpha \alpha}, l_{A}\right)+\alpha L_{a d v}\left(x_{B B}, y_{\alpha \alpha}, l_{B}\right) \\ L_{p i x}^{m r p} &=\left\|x_{\alpha \alpha}-y_{\alpha \alpha}\right\|_{1} \\ \text { where } y_{\alpha \alpha} &=F\left(c_{\alpha}, s_{\alpha}\right)=G\left(x_{A A}, x_{B B}, \alpha, \alpha\right) \end{aligned}
Swapping Loss
形状と外観を入れ替えるような生成画像は、指定した外観としてDiscriminatorを騙せることが期待されます。
- $(a_c, a_s) = (0, 1)$のときの出力画像$y_{AB}$は、$x_{BB}$と似た外観になる。
- $(a_c, a_s) = (1, 0)$のときの出力画像$y_{BA}$は、$x_{AA}$と似た外観になる。
このような生成画像は、外観に関する期待しかできないので、敵対的損失は適用できますが、Pixel損失は適用できません。
\begin{aligned} L_{a d v}^{s w p} &=L_{a d v}\left(x_{A A}, y_{B A}, l_{A}\right)+L_{a d v}\left(x_{B B}, y_{A B}, l_{B}\right) \\ \text { where } y_{A B} &=F\left(E_{c}\left(x_{A A}\right), E_{s}\left(x_{B B}\right)\right)=G\left(x_{A A}, x_{B B}, 0,1\right) \\ y_{B A} &=F\left(E_{c}\left(x_{B B}\right), E_{s}\left(x_{A A}\right)\right)=G\left(x_{A A}, x_{B B}, 1,0\right) \end{aligned}
Cycle-swapping Loss
サイクル損失は、一度別の外観にした画像を、元の外観に戻したときに、最初の画像に戻ってくるかを表す損失です。
本手法では、以下のような手順を踏みます。
- 入力画像$x_{AA}, x_{BB}$に対して$(a_c, a_s) = (0, 1), (1, 0)$として、画像$y_{AB}, y_{BA}$を得る。
- 入力画像$y_{AB}, y_{BA}$に対して$(a_c, a_s) = (0, 1), (1, 0)$として、画像$y^\prime_{AA}, y^\prime_{BB}$を得る。$y^\prime_{AA}, y^\prime_{BB}$は、それぞれ最初の入力画像$x_{AA}, x_{BB}$に近い画像となることが期待される。
\begin{aligned} L_{a d v}^{c y c} &=L_{a d v}\left(x_{A A}, y_{A A}^{\prime}, l_{A}\right)+L_{a d v}\left(x_{B B}, y_{B B}^{\prime}, l_{B}\right) \\ L_{p i x}^{c y c} &=\left\|x_{A A}-y_{A A}^{\prime}\right\|_{1}+\left\|x_{B B}-y_{B B}^{\prime}\right\|_{1} \\ \text { where } y_{A A}^{\prime} &=F\left(E_{c}\left(y_{A B}\right), E_{s}\left(x_{A A}\right)\right)=G\left(y_{A B}, x_{A A}, 0,1\right) \\ y_{B B}^{\prime} &=F\left(E_{c}\left(y_{B A}\right), E_{S}\left(x_{B B}\right)\right)=G\left(y_{B A}, x_{B B}, 0,1\right) \end{aligned}
最終的な損失関数
以上のような損失関数を組み合わせて、最終的には以下のような損失関数が得られます。
\begin{aligned}
G^{*} &=\arg \min _{G} \max _{D} \mathcal{L}_{a d v}+\lambda \mathcal{L}_{p i x} \\
\text { where } \mathcal{L}_{a d v} &=L_{a d v}^{i d t}+L_{a d v}^{m r p}+L_{a d v}^{s w p}+L_{a d v}^{c y c} \\
\mathcal{L}_{p i x} &=L_{p i x}^{i d t}+L_{p i x}^{m r p}+L_{p i x}^{c y c}
\end{aligned}
アプリケーション
本手法は形状と外観を独立してコントロールすることができるので、以下のようなアプリケーションが可能になります。
Multi Image Morphing
訓練中は2つの画像しか使っていませんが、本質的にはさらに多くの枚数の画像の形状や外観を混合させることができます。また、形状と外観は独立して変化させることも可能です。
以下の画像では、4枚の画像を元にしたモーフィング結果が示されています。左は、形状と外観を合わせてモーフィングした例です。真ん中は、外観は平均的なものに固定し、形状のみを遷移させた例です。右は、形状を平均的なものに固定し、外観のみを遷移させた例です。
Video Frame Interpolation
外観を固定したまま形状のみをコントロールすることができるため、動画中の特定の2つのフレームの間のフレームを補間することができます。
以下の画像では、既存のフレーム補間手法とほぼ同様に、犬の鼻が徐々に現れるという結果が得られることを示しています。
Appearance Transfer
形状を固定したまま外観のみを変化させると、いわゆるスタイル変換も当然可能です。
まとめ
簡単にですが、Neural Crossbreedについてまとめてみました。教師モデルであるBigGANのモーフィング結果である$x_{\alpha\alpha}$もうまく訓練に取り込んでいるのが面白いところだと思いました。もちろん、潜在空間における補間が十分に働く教師モデルを選ぶ必要があるので、ある程度信頼のおける学習済みモデルを使う必要がありそうです。