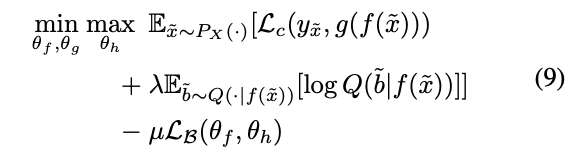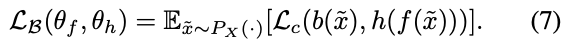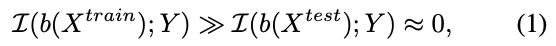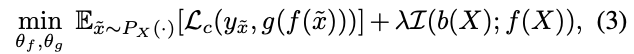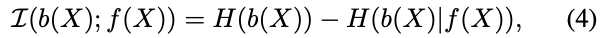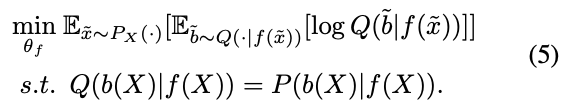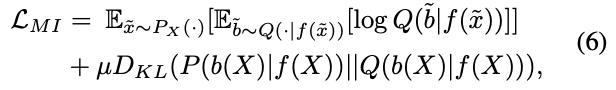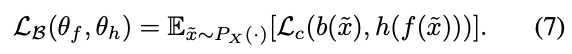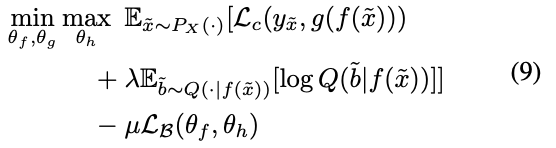概要
本論文では、深層学習においてデータに含まれるバイアスを取り除くことで正則化を行う手法を提案している。タイトルの通りに、「何を学ばないかを学ぶ」ために、学んではいけない情報(=バイアスのラベル)を与え、GANsの枠組みを用いてデータに含まれるバイアスの影響を取り除こうとする。
わかりやすい例として、本論文の実験で使用しているColored MNISTのデータを示す。

上図からわかるように、Trainデータでは、0は赤、1は緑といった具合に、色とクラストの相関が高いが、Testデータではそのような相関はないデータセットを考える。このデータセットは、色というバイアスが強くかかっているデータであると言える。
このような場合、Trainデータから「形状によって分類するモデル」ではなく、「色によって分類するモデル」ができてしまう可能性がある。
そこで、本手法では、Trainに存在するバイアス(Colored MNISTでは、各数字の色であるRGBの値)を知っている前提で、それを反映していないモデルを構築することを目指す。
注意:この文書は荒いメモなので、細かい内容に関してはご自身で元論文に当たるなどしてください
論文情報
著者
- Byungju Kim(School of Electrical Engineering, KAIST, South Korea)
- Hyunwoo Kim(Beijing Institute of Technology)
- Kyungsu Kim(Samsung Research)
- Sungjin Kim(Samsung Research)
- Junmo Kim(School of Electrical Engineering, KAIST, South Korea)
学会・ジャーナル
手法
ネットワークの構造と学習手順
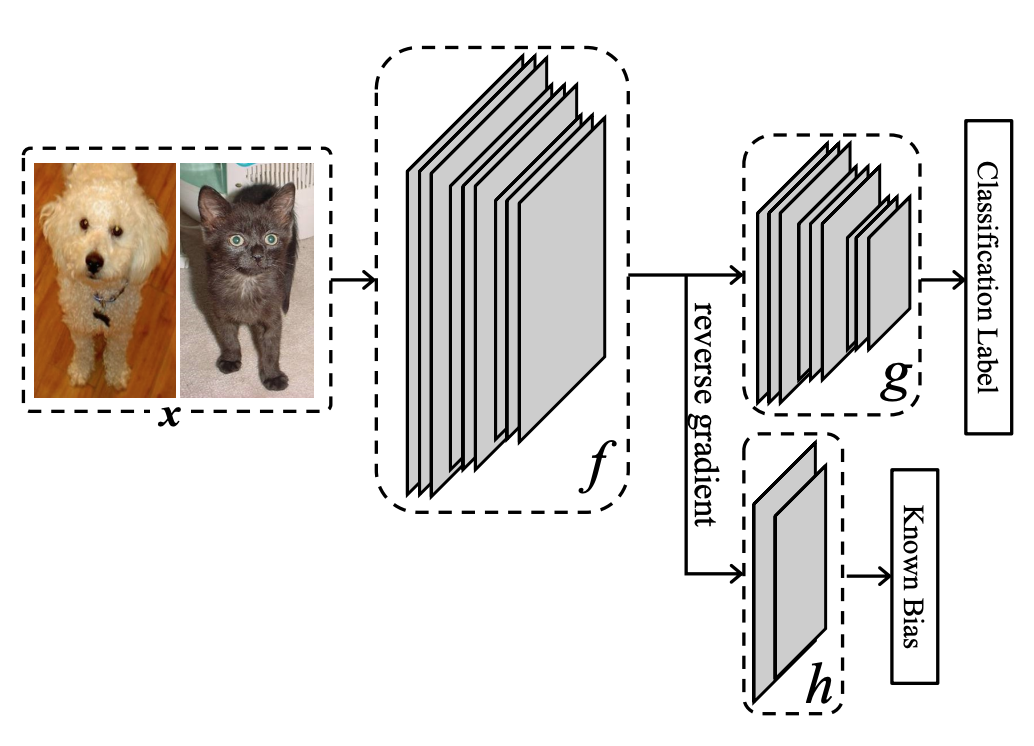
理論的な説明の前に、直感的な理解を得るために、ネットワークの構造と学習手順を示す。
入力画像$x$を$f$を通すことで、いわば特徴量を得る。特徴量は通常の分類ラベルを予測するルートである$g$と、バイアスのラベル(Colored MNISTであればRGBの値)を予測するルートである$h$とに入力さる。
本手法の目的は、$g \circ f$によってクラス分類できるように学習しつつも、$h \circ f$によってバイアスを分類できないようにすることである。そのためには、$f(x)$がクラス分類に必要な情報を十分に含んでいると同時に、バイアスを分類するのに必要な情報を含んでいないことが求められる。
このような最適化問題を解くためには、以下のようなGANs風の学習手順を採用すればよい。
- $f, g$を固定し、バイアスを分類できるように$h$を訓練する。
- $h$を固定し、クラス分類できるように$g \circ f$を訓練しつつ、$f(X)$とバイアスが無関係になるように$f$を訓練する。これは、$h \circ f$の分類が外れるように訓練することとを意味しないことに注意。というのも、完全にバイアス分類を外す$f(x)$というのは、むしろバイアスの情報を反映してしまっていることになるからである。
理論と定式化
見通しをよくするために、最終的に得られる最適化問題を先に示しておく。細かい数式に興味のない方は、ここだけ見ておけば良いと思う。
1行目はクラス分類誤差を表現し、3行目はバイアス分類誤差を表現している。
ちなみに、3行目の$L_B(\theta_f, \theta_h)$は、具体的には以下のような形をしている。シンプルな分類誤差であることがわかる。
よくわからないのは、(9)式の2行目だと思う。$Q$は、実装上は$h(f(X))$の出力にsoftmaxを適用したものである。そのため、$\min_{\theta_f, \theta_g}$にも$\max_{\theta_h}$にも関係する項と考えられる。しかし、この項は、出力分布が偏っていると大きくなり、ばらけていると小さくなる。$\max_{\theta_h}$からみるとこの項の意味はほとんどなく、数式の解釈によっては$\max_{\theta_h}$は$Q$に関わる部分に対して適用する必要はないかもしれない。一方で、$\min_{\theta_f}$からみると、出力分布が平坦になるように$f$を訓練することになるので、「完全にバイアス分類を外すf(x)f(x)というのは、むしろバイアスの情報を反映してしまっている」という先に述べた問題を回避するための項であると解釈できる。
記号の整理
まず、簡単に記号の整理をしておく。
- 入力画像とその集合: $x \in X$
- 分類ラベルとその集合: $y \in Y$
- 入力画像$x$の分類ラベルは、$y_x$と表現されている。
- バイアスラベルの集合: $B$
- $x$からそのバイアスへの写像: $b: X \rightarrow B$:
- 入力画像$x$のバイアスラベルは$b(x)$と表される。
- 特徴量の次元数: $K$
- $x$から特徴量を求める関数: $f: X \rightarrow \mathbb{R}^K$
- 特徴量から分類ラベルを求める関数: $g: \mathbb{R}^K \rightarrow Y$
- 特徴量からバイアスを求める関数 $h: \mathbb{R}^K \rightarrow B$
- 特徴量が既知の時のバイアスの条件付き確率分布(事後分布): $P$
- $P$を近似する確率分布: $Q$
バイアスの定義
教師データに関してのみ、分類ラベルとの相互情報量が大きくなる関数$b$が存在する時、それをバイアスと呼ぶ。
バイアスの問題は、教師データによって訓練されたネットワークが下式のような結果をもたらし、テストデータに対する精度が悪くなってしまうことにある。。
学習の目的は、この相互情報量を最小化する$f, g$を求めることであるが、実際には、最小化したい相互情報量は$I(b(X); f(X))$として良いものとする。$f(x)$から$b(x)$に関する情報を取り除きさえすれば、$I(b(X); g(f(X))$)が小さくなることは自明である。
目的関数とその変形
以上を踏まえて、ネットワークの学習の目的関数は、さしあたっては以下のようにできる。分類誤差を最小化しつつも、バイアスも小さくする、という形になっている。
バイアスを表す相互情報量は、以下のようにエントロピーと条件付きエントロピーに分解できる。
右辺第1項は定数なので、第2項の負の条件付きエントロピー$-H(b(X) \mid f(X))$を最小化すればよい。条件付きエントロピーは、$f(x)$から得られた時の$b(x)$の乱雑さ(予測しにくさ)を表しているので、負の条件付きエントロピーを最小化する$f$を求めることは、$b(x)$を予測しにくい$f$を得ることを意味する。
ここで、条件付き分布$P(b(X) \mid f(X))$を求めたいところだが、直接扱うのは難しいため、これを近似する$Q$を想定すれば、最小化対象は以下のように書き直せる。1行目は、$-H(b(x) \mid f(X))$そのものの$P$を$Q$に置き換えたものであり、2行目の制約によって$Q$は$P$を近似しているということを表している。
$s.t. Q=P$満たす$Q$を得るためには、また別の最適化問題を解く必要がある。$Q$による$P$の近似を、$D_{KL}(P \mid \mid Q)$の最小化問題として捉えると、(5)式は以下の損失を最小化することで行える。(5)式のs.t.の部分が$D_{KL}$の項に対応している。
(6)式の$D_{KL}$を最小化することは、要するに、$f(X)$が与えられた時に$b(X)$(の分布)を予測できる$h$を訓練することに相当する。そのため、意味的には下記損失を最小化すれば、(6)式の$D_{KL}$は最小化できると考えてよい。
そのため、(6)式の損失の最小化は、以下のようなmin-max最適化に帰着できる。
これまでの変形を(3)式に反映することで、最初に示した最適化問題が導ける。
実験
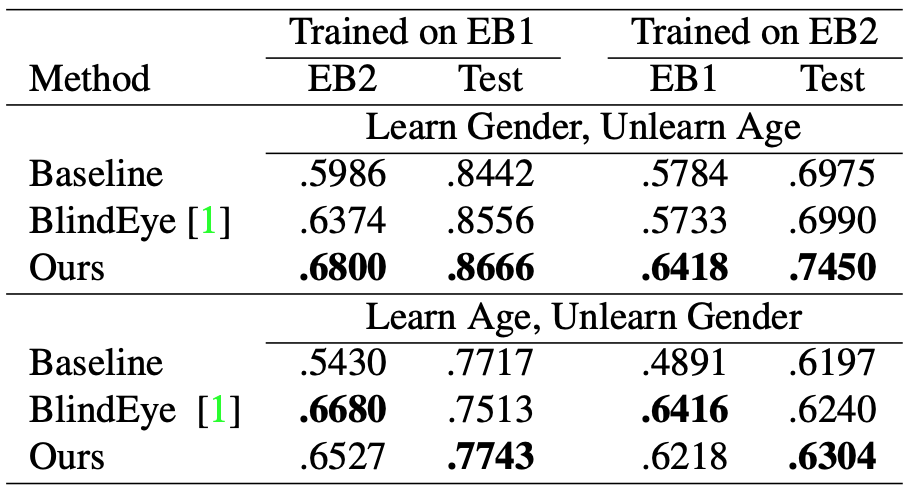
理論の説明で疲れたのであまり詳しくは書かないが、IMDB faceデータセットを使った問題設定が面白い。AgeとGenderが完全に紐づいてしまっているデータから、Ageの影響を抑えたGender分類器を作ったり、Genderの影響を抑えたAge分類器を作ろうとしている。
以下が結果である。
議論
省略
感想
いわゆるDisentangleの一手法。
本手法で使われている、さらっと触れられているGradient Reversal Layerについて、あまり理解できていないので、元になっている論文(Unsupervised Domain Adaptation by Backpropagation)も読んでみたい。