この記事は iOSDC2020の原稿と詳解を兼ねた記事です。
自己紹介
カビゴン小野と申します。
アプリエンジニア、インフラエンジニアとして働いています。
Swift、Terraform、カビゴンが好きです。
基礎
ベジェ曲線
今回はベジェ曲線について話させていただきます。
ベジェ曲線は、シトロエン社のド・カステリョとルノー社のピエール・ベジェにより考案されました。
ベジェ曲線はアプリのアイコンやアニメーション、ポスターなど様々な箇所で用いられ、私たちの身の回りは実はベジェ曲線で溢れています。
iOSエンジニアの身近なところでは、会社のロゴやアプリのアイコンなどもベジェ曲線から作られています。
ベジェ曲線の数式
ベジェ曲線を構成する制御点を $ p_0,\ p_1,\ ...,\ p_n$ とすると、n次のベジェ曲線は以下の式で与えられます。
Q(t)=\sum_{i=0}^{n-1} p_iB^{n-1}_i(t) \ \ (0 \leqq t \leqq 1)
ここで$ B^n_i(t) $ はバーンスタイン多項式と呼ばれ、以下の式で表されます。
B^n_i(t)=\binom{n}{i}t^j(1-t)^{n-1}
係数は二項係数と呼ばれる係数で、以下の式で表されます。
\binom{n}{i}=\frac{n!}{(n-i)!i!} \ \ (i=0, 1, 2, ...n)
いきなり数式が現れてもイメージが沸きませんよね。
まずはベジェ曲線に慣れるためにベジェ曲線を手で書いてみましょう。
フリーハンドで書いてみよう
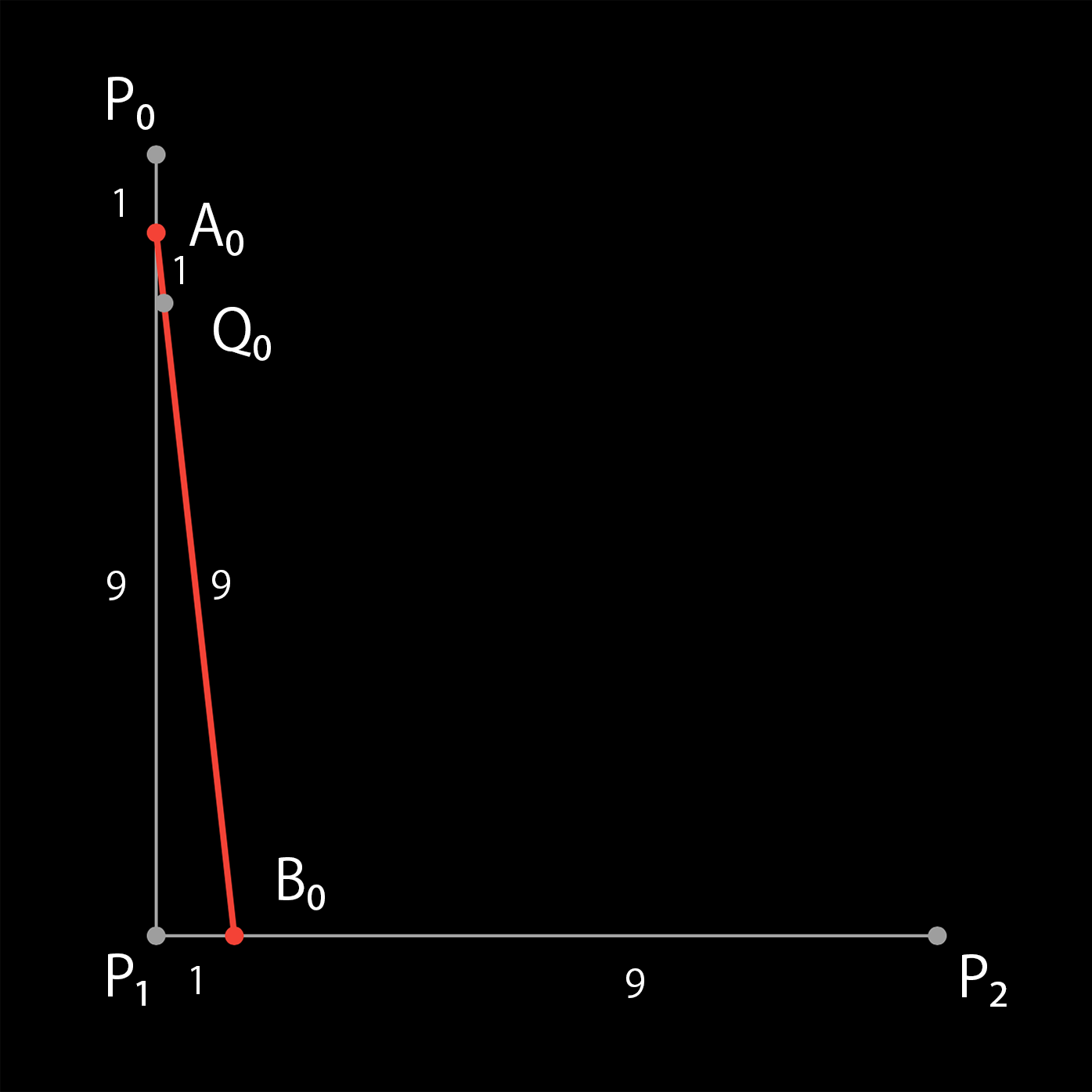
3つの制御点 $ p_0,\ p_1,\ p_2$ からなる2次のベジェ曲線をフリーハンドで作図します。
線分 $ p_0P_1 $ を 1:9、線分 $P_1P_2 $ を 1:9 に内分する点 $A_0,\ B_0 $ を求め、線分 $ A_0B_0 $ を 1:9 に内分する点 $ Q_0 $ を求めます。
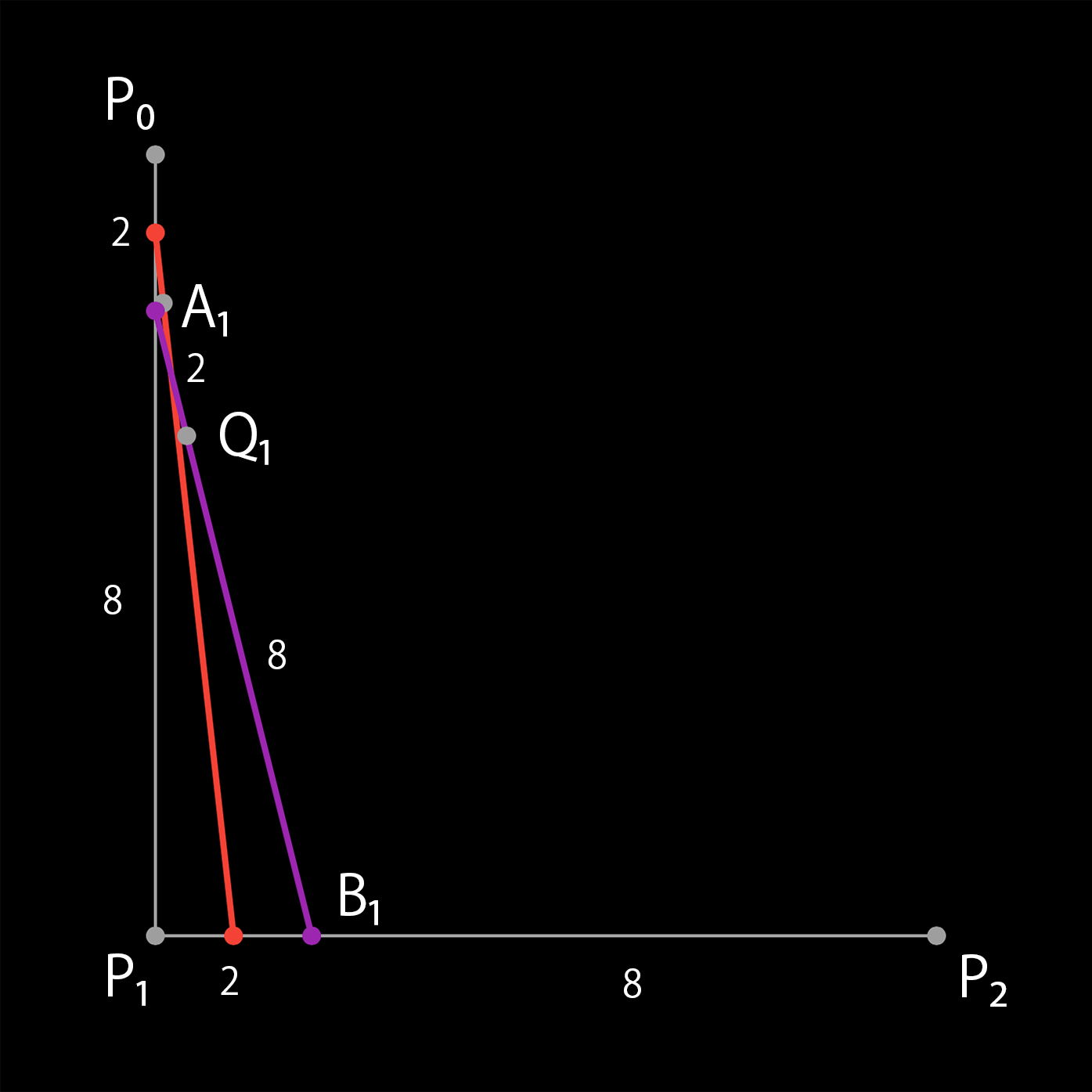
同様に線分 $ p_0p_1 $ を 2:8、線分 $P_1P_2 $ を 8:2 に内分する点 $A_1,\ B_1 $ を求め、線分 $ A_1B_1 $ を 2:8 に内分する点 $ Q_1 $ を求めます。
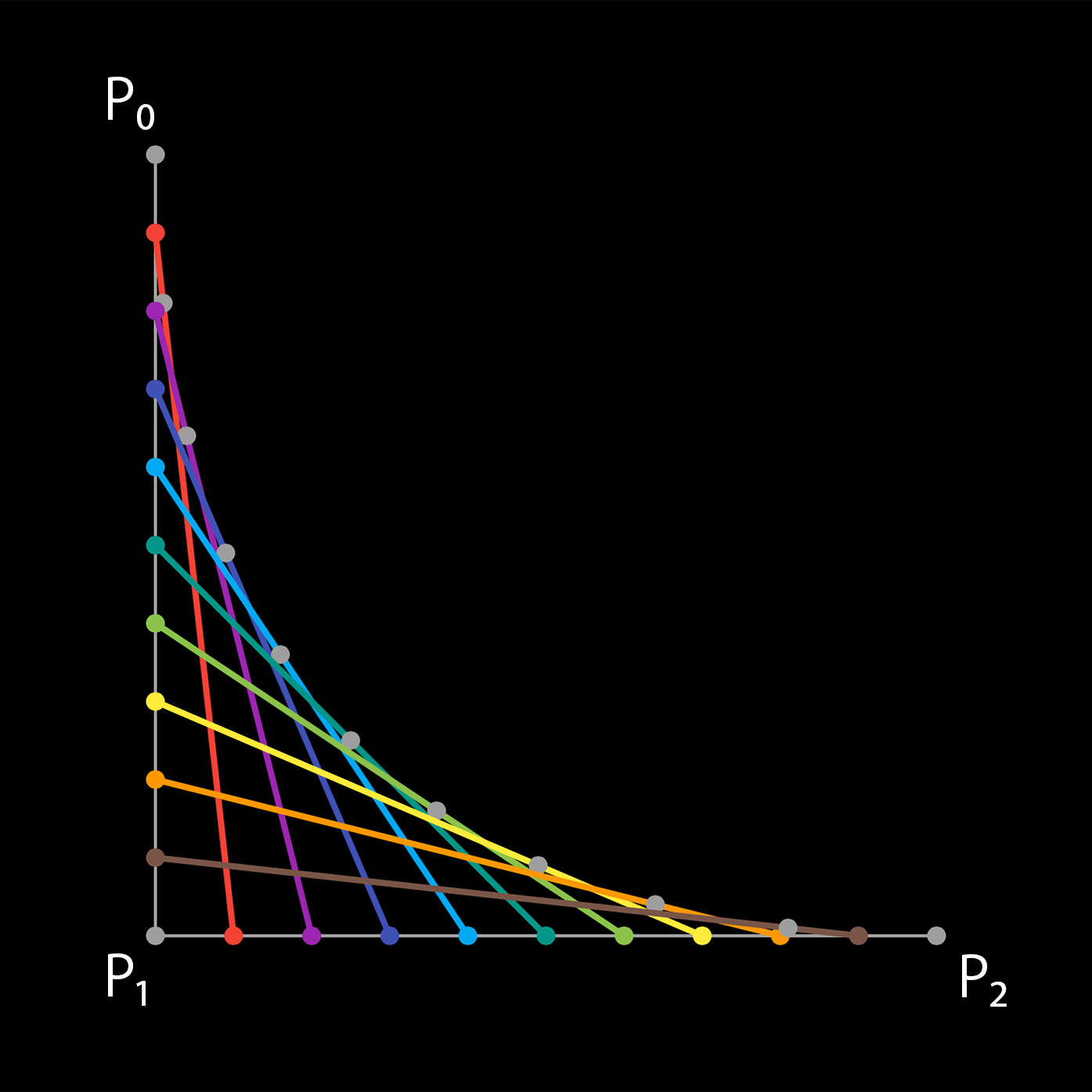
この操作を繰り返し、点 $ Q_n $ を多く求めます。
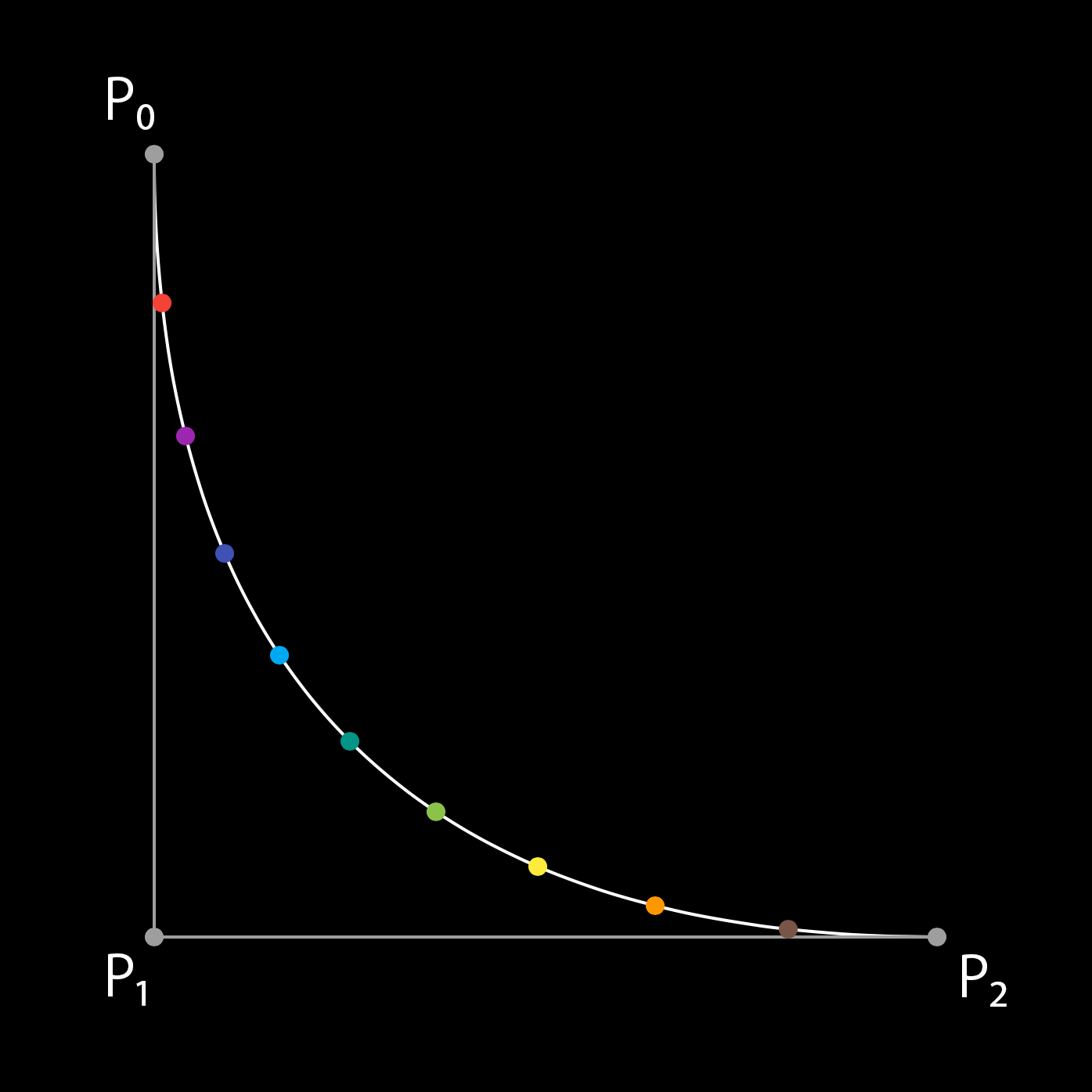
得られた点 $ Q_n $ を結ぶことでベジェ曲線が得られます。
手順は多いですが、簡単にベジェ曲線を描くことができました。
なんとなくベジェ曲線のイメージがついたでしょうか?
2次のベジェ曲線を数式で
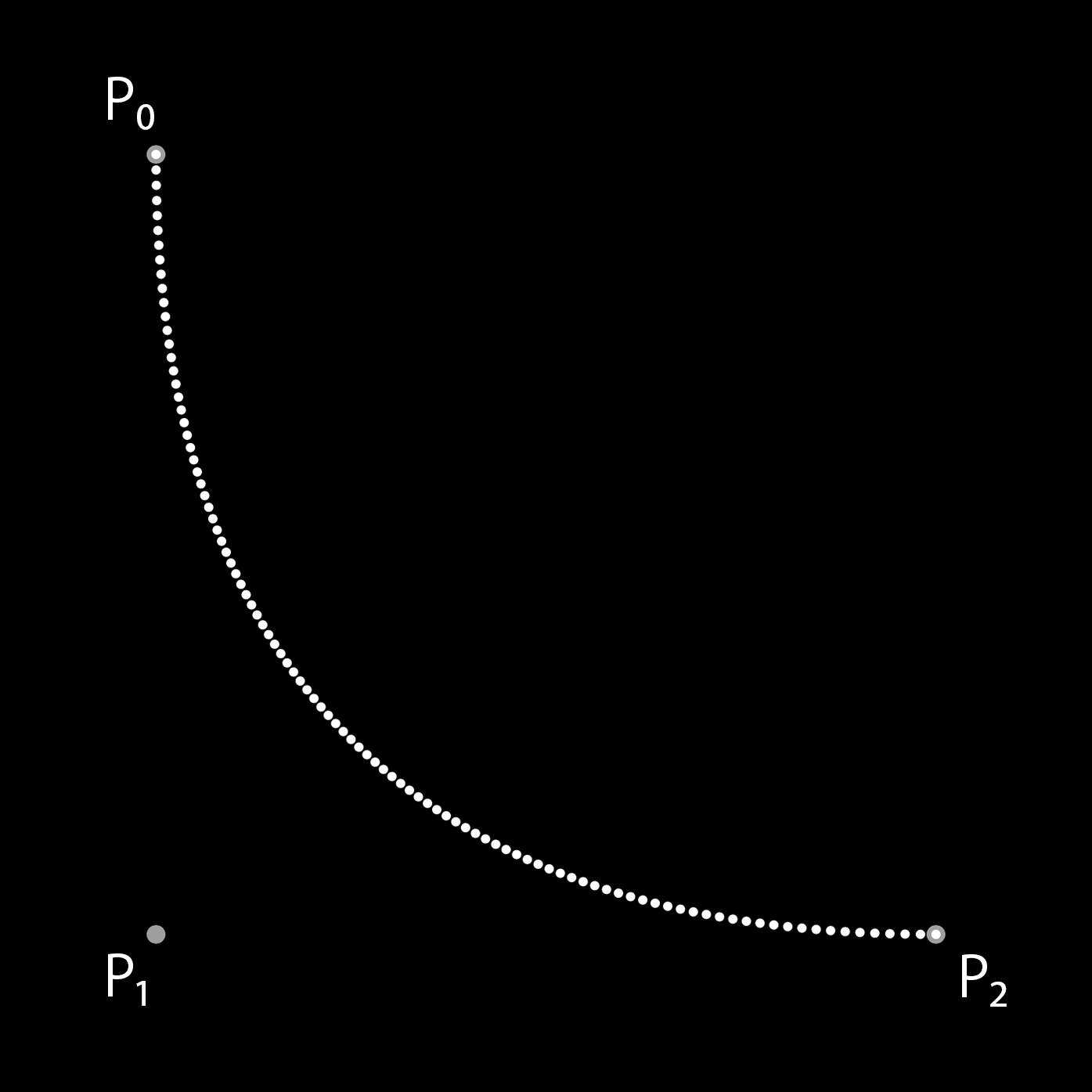
それでは今度は Swift でベジェ曲線を書いてみましょう。
フリーハンドで求めたときと同じく、3つの制御点からなる2次のベジェ曲線を書いてみます。
2次のベジェ曲線なので、$ n=2,\ i=0,\ 1,\ 2 $。
二項係数はそれぞれ $ 1,\ 2,\ 1 $ です。
\binom{2}{0}=1,\ \binom{2}{1}=2,\ \binom{2}{2}=1
つまり、$ n=2 $ におけるバーンスタイン多項式は以下の式で表されます。
\begin{align*}
& B^2_0(t)=(1-t)^2 \\
& B^2_1(t)=2t(1-t) \\
& B^2_2(t)=t^2
\end{align*}
ベジェ曲線はバーンスタイン多項式と制御点の積の和で表されるため、2次のベジェ曲線の式は以下の式で表されます。
\begin{align*}
& Q(t)=\sum_{i=0}^n P_iB^n_i(t)=p_0B^2_0(t)+p_1B^2_1(t)+p_2B^2_2(t) \\
& =p_0(1-t)^2+2P_1t(1-t)+P_2t^2 \ \ (0 \leqq t \leqq 1)
\end{align*}
Swiftでこの式を以下のように書くことができます。
func bezirPoint(t: Double) -> Point {
let x = pow((1.0 - t), 2) * p0.x + 2 * t * (1.0 - t) * p1.x + pow(t, 2) * p2.x
let y = pow((1.0 - t), 2) * p0.y + 2 * t * (1.0 - t) * p1.y + pow(t, 2) * p2.y
return Point(x: x, y: y)
}
for i in 0...100 {
let t = 0.01 * Double(i)
let point = bezirPoint(t: t)
addPoint(point: point, color: .white, lineWidth: 2)
}
このコードを実行するとベジェ曲線に沿って点が描画されます。
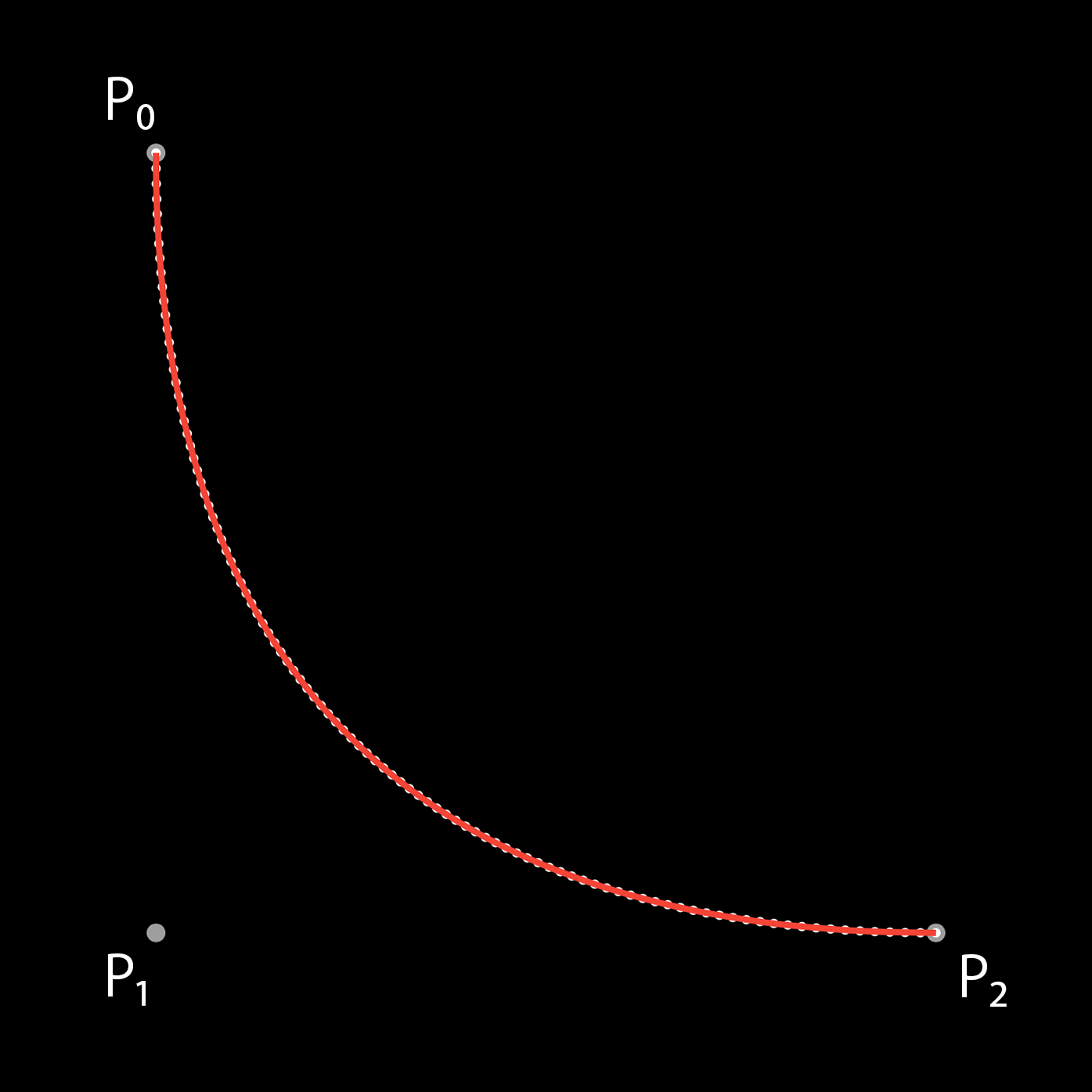
iOSの UIBezierPath.addCurve(to:controlPoint:) は2次のベジェ曲線を作成するためのメソッドです。
赤い線が addCurveメソッドで描画したベジェ曲線です。
先ほど点で描画された箇所と一致することがわかります。
3次のベジェ曲線を数式で
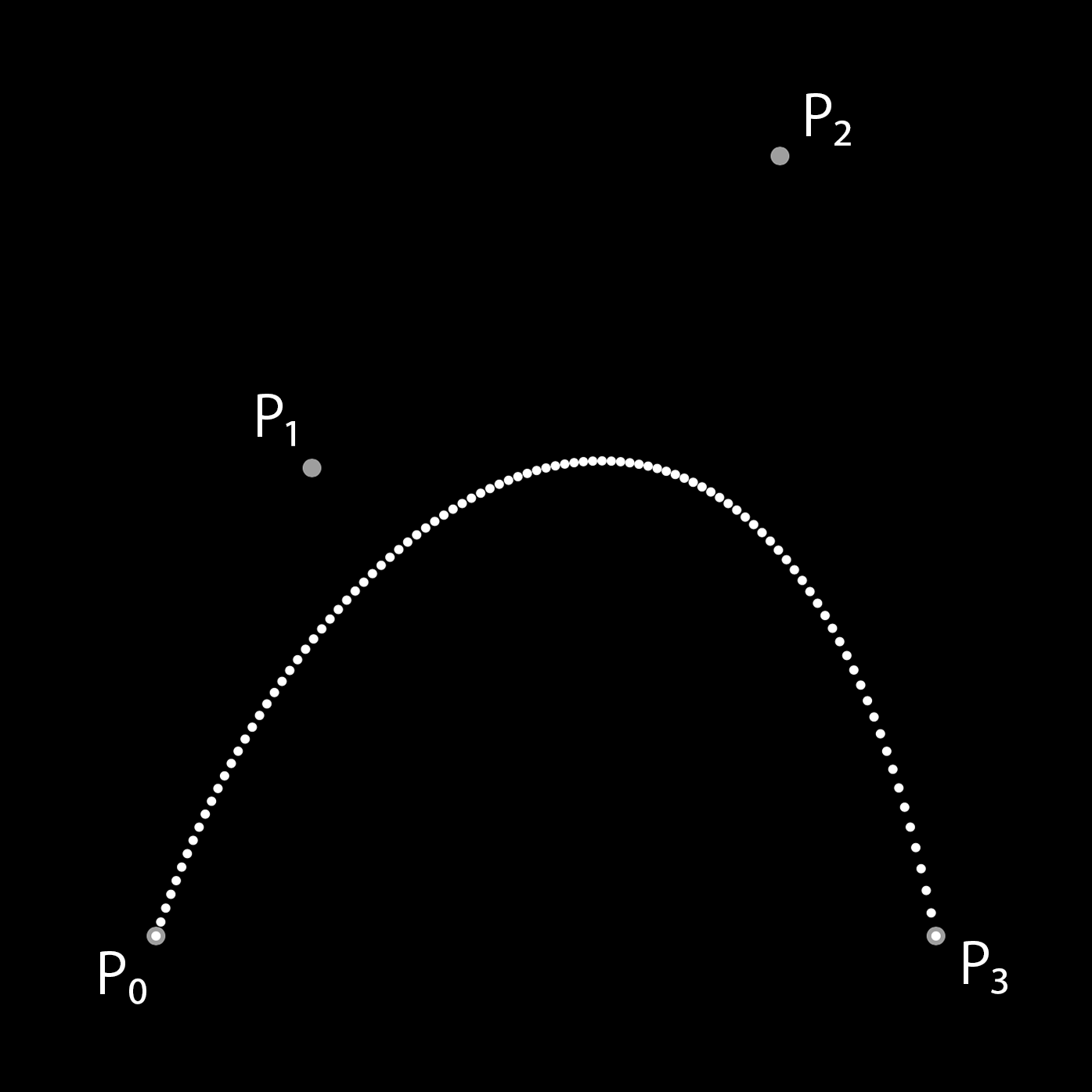
制御点が4点からなる3次のベジェ曲線も同様に考えます。
3次のベジェ曲線なので、$ n=3,\ i=0,\ 1,\ 2,\ 3 $。
二項係数はそれぞれ $ 1,\ 3,\ 3,\ 1 $ です。
\binom{3}{0}=1,\ \binom{3}{1}=3,\ \binom{3}{2}=3,\ \binom{3}{3}=1
つまり、$ n=3 $ におけるバーンスタイン多項式は以下の式で表されます。
\begin{align*}
& B^3_0(t)=(1-t)^3 \\
& B^3_1(t)=3t(1-t)^2 \\
& B^3_2(t)=3t^2(1-t) \\
& B^3_3(t)=t^3
\end{align*}
3次のベジェ曲線の式は以下で表されます。
\begin{align*}
& Q(t)=\sum_{i=0}^n P_iB^n_i(t)=P_0B^3_0(t)+P_1B^3_1(t)+P_2B^3_2(t)+P_3B^3_3(t) \\
& =P_0(1-t)^3+3P_1t(1-t)^2+3P_2t^2(1-t)+P_3t^3 \ \ (0 \leqq t \leqq 1)
\end{align*}
これをSwiftでこのように書くことができます。
func bezirPoint(t: Double) -> Point {
let x = pow(1.0 - t, 3) * p0.x
+ 3 * t * pow(1.0 - t,2) * p1.x
+ 3 * pow(t, 2) * (1.0 - t) * p2.x
+ pow(t, 3) * p3.x
let y = pow(1.0 - t, 3) * p0.y
+ 3 * t * pow((1.0 - t),2) * p1.y
+ 3 * pow(t, 2) * (1.0 - t) * p2.y
+ pow(t, 3) * p3.y
return Point(x: x, y: y)
}
for i in 0...100 {
let t = 0.01 * Double(i)
let point = bezirPoint(t: t)
addPoint(point: point, color: .white, lineWidth: 2)
}
このコードを実行するとベジェ曲線に沿って点が描画されます。
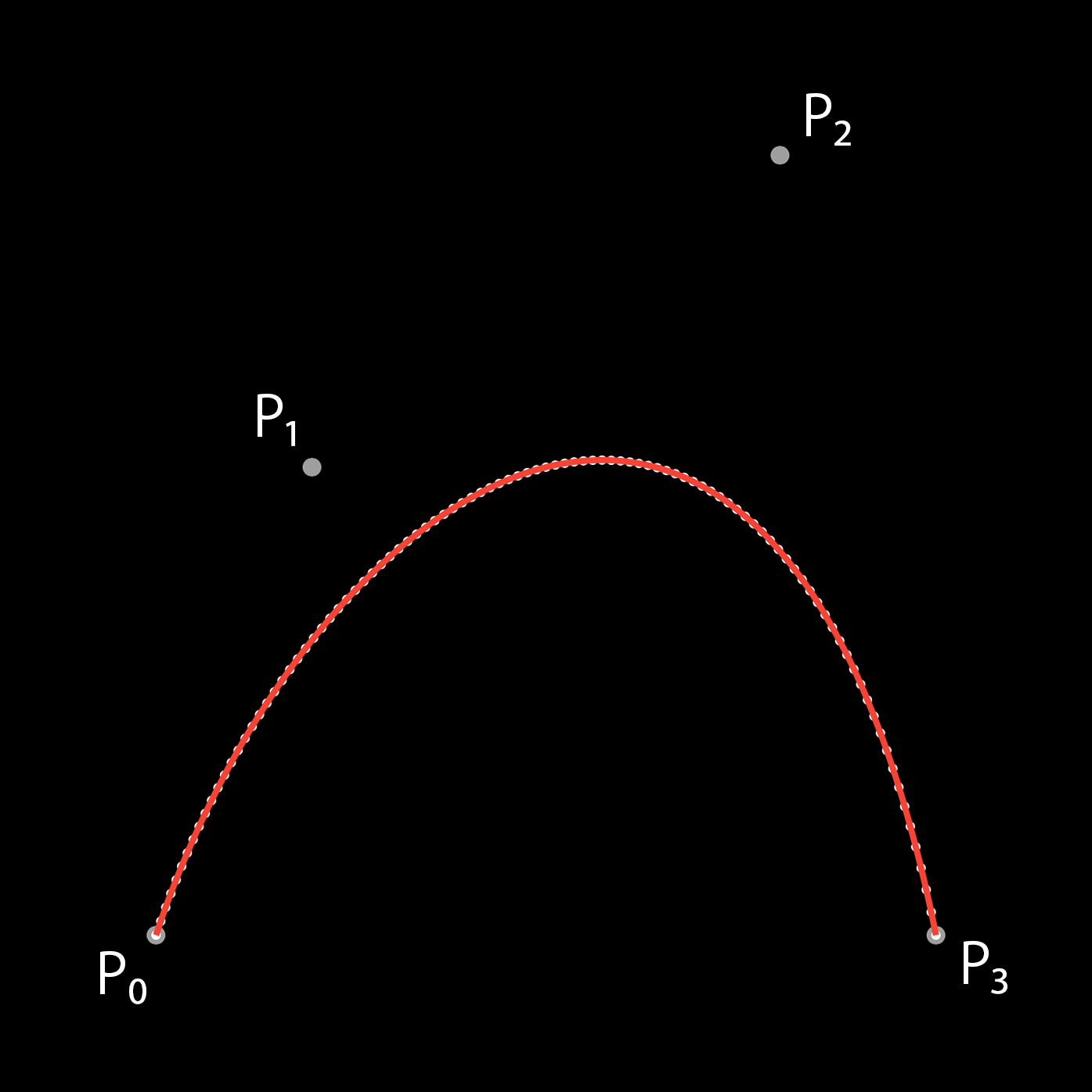
iOSの UIBezierPath.addCurve(to:controlPoint1:controlPoint2:) は3次のベジェ曲線を描画するためのメソッドです。
赤い線が addCurve メソッドで描画したものです。
先ほど作ったベジェ曲線と一致することがわかります。
ここまでのソースコードは こちら です。
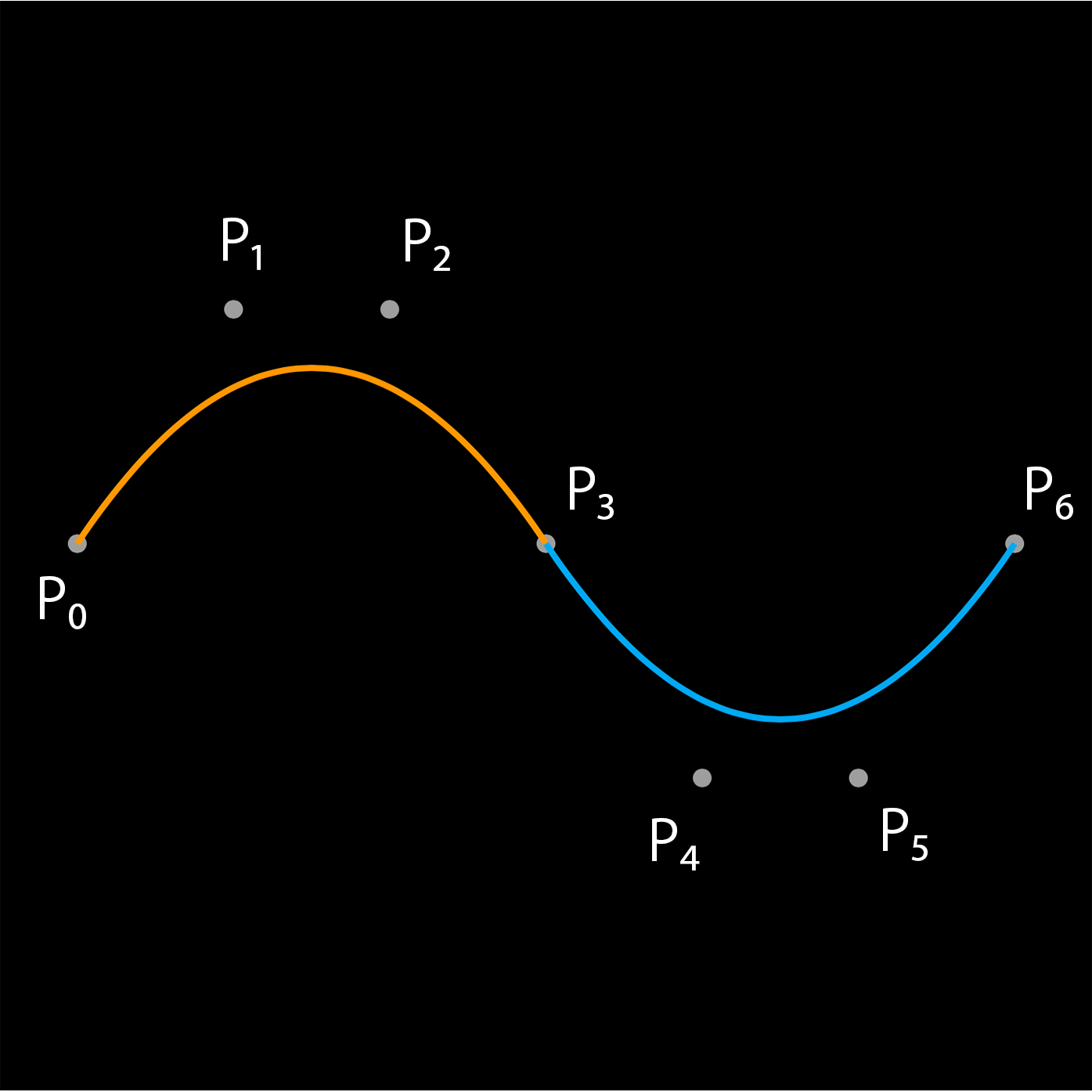
ポリベジェ曲線
しかし制御点が5つからなる4次のベジェ曲線を書くためのメソッドは UIBezierPath にはありません。
それは高次のベジェ曲線は計算コストが高いため、3次のベジェ曲線を組み合わせることで高次のベジェ曲線を書いています。
このように複数のベジェ曲線からなるベジェ曲線はポリベジェ曲線と呼ばれます。
たとえば制御点が7つからなる6次のベジェ曲線は、3次のベジェ曲線を組み合わせることで表現されます。
以下の図ではオレンジと水色のベジェ曲線からポリベジェ曲線を構成しています。
以後、ポリベジェ曲線を構成する3次のベジェ曲線を Segment と呼ぶことにします。
オレンジ色のベジェ曲線は0番目の Segment で、水色のベジェ曲線は1番目の Segment です。
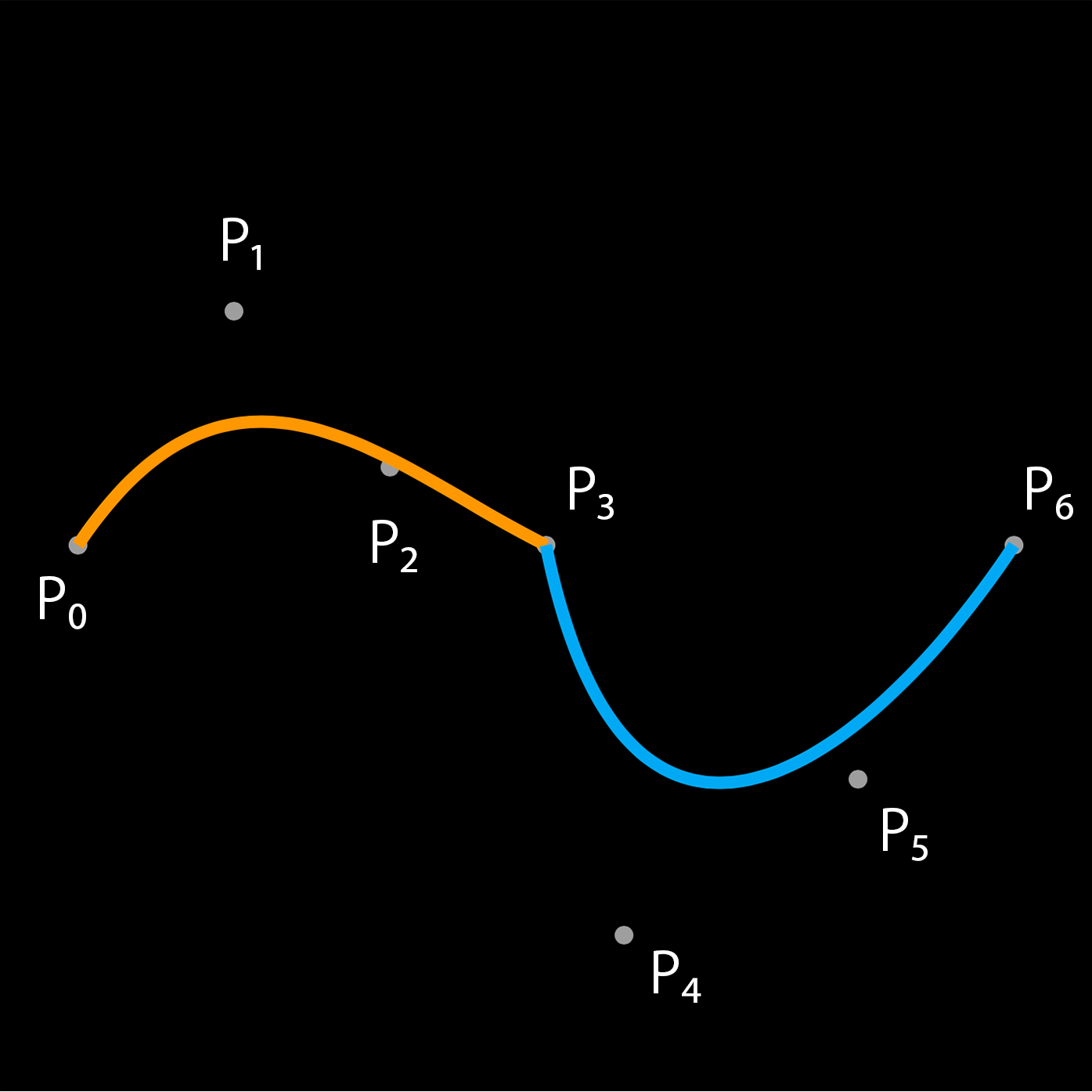
しかし Segment の始点と終点を一致させるだけではポリベジェ曲線は滑らかになりません。
Segment の終点と始点が一致しているだけではなく、終点、始点における第一次微分係数、第二次微分係数が一致する必要があります。
それらを一致させないと以下の画像のように滑らかなポリベジェ曲線が得られません。
応用
具体的な応用例
ここまでは大丈夫でしょうか?
ここからは少し応用編です。
私が実際に体験した例を踏まえてベジェ曲線の応用例を紹介します。
少し前に手書きノートアプリの開発をお手伝いすることになりました。
そのアプリの中に手書き機能があり、私はユーザーが触った座標を線で繋ぐことで手書き機能を実現しました。
このような実装です。
import UIKit
class SignViewController: UIViewController {
override func viewDidLoad() {
super.viewDidLoad()
view.backgroundColor = .white
}
override open func touchesMoved(_ touches: Set<UITouch>, with event: UIEvent?) {
guard let touch = touches.first else {
return
}
let from = touch.previousLocation(in: self.view)
let to = touch.location(in: self.view)
let path = UIBezierPath()
path.move(to: from)
path.addLine(to: to)
let color = UIColor.black
let shapeLayer = CAShapeLayer()
shapeLayer.path = path.cgPath
shapeLayer.fillColor = color.cgColor
shapeLayer.strokeColor = color.cgColor
shapeLayer.lineWidth = 4
view.layer.addSublayer(shapeLayer)
}
}
一見問題なさそうですね。
しかしこの実装では急いで書くと座標の数が足りずカクカクになってしまったり、線を太くすると文字がひび割れてしまいました。
こは直線のみで構成されているからです。
この問題をベジェ曲線を使って解決してみましょう。
座標から制御点を得る式を求める
3次のベジェ曲線は以下の式で表されます。
Q(t)=(1-t)^3p_0+3(1-t)^2tP_1+3(1-t)t^2P_2+t^3P_3 \tag{1}
この式変形をして以下の式を得ます。
Q(t)=(1-t)^3p_0+3(t-2t^2+t^3)P_1+3(t^2-t^3)P_2+t^3P_3
この式を、一次微分、二次微分することで式(2), (3)を得ます。
Q'(t)=-3(1-t)^2p_0+3(1-4t+3t^2)P_1+3(2t-3t^2)P_2+3t^2P_3 \tag{2}
Q''(t)=6(t-1)p_0+3(-4+6t)P_1+3(2-6t)P_2+6tP_3 \tag{3}
i番目の Segment の始点と (i-1)番目の Segment の終点は滑らかに接続する必要があります。
i番目の Segment の始点と(i-1)番目の Segment の第一次微分係数は一致します。
Q'_i(0)=Q'_{i-1}(1)
第一次微分係数が一致することと式(2)から式(4)が得られます。
Q'_i(0)=-3P_{0,i}+3P_{1,i}
Q'_{i-1}(1)=-3P_{2,i-1}+3P_{3,i-1}
-3P_{0,i}+3P_{1,i}=-3P_{2,i-1}+3P_{3,i-1} \tag{4}
i番目の Segment の始点と (i-1)番目の Segment の終点は一致します。
Q_i(0)=Q_{i-1}(1)
終点が一致することと式(1)から式(5)が得られます。
Q_i(0)=P_{0,i}
Q_{i-1}(1)=P_{3, i-1}
P_{0,i}=P_{3, i-1}=K_i \tag{5}
式(4)と式(5)から式(6)が得られます。
−P_{0,i} + P_{1,i} = −P_{2,i−1} + P_{3,i−1}
−K_i + P_{1,i} = −P_{2,i−1} + K_i
2K_i=P_{1,i}+P_{2,i-1} \tag{6}
i番目の Segment の始点と、(i-1)番目の Segment の終点の第二次微分係数は一致します。
Q′′_i(0) = Q′′_{i-1} (1)
式(3)から式(7), (8)が得られます。
Q′′_i(0) = 6P_{0,i} − 12P_{1,i} + 6P_{2,i} \tag{7}
Q′′_{i-1}(1) = 6P_{1,i−1} − 12P_{2,i−1} + 6P_{3,i−1} \tag{8}
式(7),(8)は等価であるため、式(9)が得られます。
6P_{0,i}-12P_{1,i}+6P_{2,i}=6P_{1,i-1}-12P_{2,i-1}+6P_{3,i-1}
P_{0,i} − 2P_{1,i} + P_{2,i} = P_{1,i−1} − 2P_{2,i−1} + P_{3,i−1} \tag{9}
式(5)と式(9)から式(10)が得られます。
K_i − 2P_{1,i} + P_{2,i} = P_{1,i−1} − 2P_{2,i−1} + K_i
-2P_{1,i}+P_{2,i}=P_{1,i-1}-2P_{2,i-1} \tag{10}
最初の Segment において $ Q′′_0(0) = 0 $ とすると式(7)から式(11)が得られます。
6P_{0,0} − 12P_{1,0} + 6P_{2,0} = 0
P_{0,0}-P_{1,0}+P_{2,0}=0
K_0 − 2P_{1,0} + P_{2,0} = 0 \tag{11}
最後のセグメントにおいて $ Q′′_{i-1}(1) = 0 $ とすると、式(5)と式(8)から式(12)が得られます。
6P_{0,0} − 12P_{1,0} + 6P_{2,0} = 0
P_{1,n−1} − 2P_{2,n−1} + P_{3,n−1} = 0
P_{1,n−1} − 2P_{2,n−1} + K_{n} = 0 \tag{12}
式(6)より以下の式が得られます。
P_{2,i−1} = 2K_{i} − P_{1,i}
P_{2,i} = 2K_{i+1} − P_{1,i+1}
この式と式(10)より式(A)が得られます。
−2P_{1,i} + 2K_{i+1} − P_{1,i+1} = P_{1,i−1} − 2(2K_i − P_{1,i})
P_{1,i−1} + 4P_{1,i} + P_{1,i+1} = 4K_1 + 2K_{i+1} \tag{A}
式(6)より以下の式が得られます。
P_{2,0} = 2K_1 − P_{1,1}
この式と式(11)より式(B)が得られます。
K_0 −2P_{1,0} + 2K_1 −P_{1,1} = 0
2P_{1,0} +P_{1,1} = K_0 +2K_1 \tag{B}
式(6)より以下の式が得られます。
P_{2,n−1} = 2K_n − P_{1,n}
この式と式(12)より式(13)が得られます。
P_{1,n−1} − 2(2K_n − P_{1,n}) + K_n = 0
P_{1,n−1} + 2P_{1,n} = 3K_n \tag{13}
式(A)が $ i=n-1 $で成り立つとすると、式(14)が得られます。
P_{1,n−2} + 4P_{1,n−1} + P_{1,n} = 4K_{n−1} + 2K_n \tag{14}
$ 式(14) \times 2 - 式(13)$ より、式(C)が得られます。
2P_{1,n−2} + 7P_{1,n−1} = 8K_{n−1} + K_n \tag{C}
$ P_2 $ についても同様に式(D)を得られます。
式(6)と式(12)より、式(D), (E)が得られます。
P_{2,i}=2K_i-P_{1,i}
P_{2,n-1}=\frac{1}{2}(K_n+P_{i,n-1}) \tag{D}
P_{2,i-1}=P_{1,i} - 2K_i \tag{E}
式(A),(B),(C),(D),(E)を求めることができました。
この式を使うことで、式(A),(B),(C),(D),(E)手書きの座標のデータから滑らかな曲線へと変換することが可能になります。
P_{1,i−1} + 4P_{1,i} + P_{1,i+1} = 4K_1 + 2K_{i+1} \tag{A}
2P_{1,0} +P_{1,1} = K_0 +2K_1 \tag{B}
2P_{1,n−2} + 7P_{1,n−1} = 8K_{n−1} + K_n \tag{C}
P_{2,n-1}=\frac{1}{2}(K_n+P_{i,n-1}) \tag{D}
P_{2,i-1}=P_{1,i} - 2K_i \tag{E}
例えば9点からなる8個のポリベジェ曲線を求める式は以下の式で表されます。
$ i=0 $
2P_{1,0} + P_{1,1} = K_0 + 2K_1
$ i=1 $
P_{1,0} + 4P_{1,1} + P_{1,2} = 4K_1 + 2K_2
$ i=2 $
P_{1,1} + 4P_{1,2} + P_{1,3} = 4K_2 + 2K_3
$ i=3 $
P_{1,2} + 4P_{1,3} + P_{1,4} = 4K_3 + 2K_4
$ i=4 $
P_{1,3} + 4P_{1,4} + P_{1,5} = 4K_4 + 2K_5
$ i=5 $
P_{1,4} + 4P_{1,5} + P_{1,6} = 4K_5 + 2K_6
$ i=6 $
P_{1,5} + 4P_{1,6} + P_{1,7} = 4K_6 + 2K_7
$ i=7 $
P_{1,6} + 4P_{1,7} + P_{1,8} = 4K_7 + 2K_8
$ i=8 $
2P_{1,7} + 4P_{1,8} = 8K_8 + K_9
この連立方程式を解くことで $ P_{1,0},\ P_{1,1},\ P_{1,2},\ P_{1,3},\ ... P_{1,8} $ を求めることができます。
プログラムで計算しやすいようにこの計算式を行列に変換します。
\left(
\begin{array}{ccc}
2 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
1 & 4 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 1 & 4 & 1 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 1 & 4 & 1 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 & 4 & 1 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 & 4 & 1 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 1 & 4 & 1 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 1 & 4 & 1 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 2 & 7
\end{array}
\right)
\left(
\begin{array}{ccc}
P_{1,0} \\
P_{1,1} \\
P_{1,2} \\
P_{1,3} \\
P_{1,4} \\
P_{1,5} \\
P_{1,6} \\
P_{1,7} \\
P_{1,8}
\end{array}
\right) =
\left(
\begin{array}{ccc}
K_0 + 2K_1 \\
4K_1 + 2K_2 \\
4K_2 + 2K_3 \\
4K_3 + 2K_4 \\
4K_4 + 2K_5 \\
4K_5 + 2K_6 \\
4K_6 + 2K_7 \\
4K_7 + 2K_8 \\
8K_8 + K_9
\end{array}
\right)
行列に変換することでTomasのアルゴリズムを適用することができます。
Tomasのアルゴリズム
Tomasのアルゴリズムは以下のような形式の連立方程式を特くためのアルゴリズムです。
\left(
\begin{array}{ccc}
b_1 & c_1 & 0 & 0 & 0 & \cdots & 0 \\
a_2 & b_2 & c_2 & 0 & 0 & \cdots & 0 \\
0 & a_3 & b_3 & c_3 & 0 & \cdots & 0 \\
0 & 0 & a_4 & b_4 & c_4 & \cdots & 0 \\
\vdots & \vdots & \vdots & \vdots & \vdots & \ddots & 0 \\
0 & 0 & 0 & 0 & a_{n-1} & b_{n-1} & c_{n-1} \\
0 & 0 & 0 & 0 & 0 & a_n & b_n
\end{array}
\right)
\left(
\begin{array}{ccc}
x_1 \\
x_2 \\
x_3 \\
x_4 \\
\vdots \\
x_{n-1} \\
x_n
\end{array}
\right) =
\left(
\begin{array}{ccc}
d_1 \\
d_2 \\
d_3 \\
d_4 \\
\vdots \\
d_{n-1} \\
d_n
\end{array}
\right)
1番目の式は以下の式で表されます。
b_1x_1 - c_1x_2 = d_1 \tag{1}
式(1)を変形して式(2)を得ます。
x_1 + \frac{c_1}{b_1}x_2 = \frac{d_1}{b_1} \tag{2}
ここで $ e_1,\ f_1 $ を式(3),(4)とします。
e_1 = \frac{c_1}{b_1} \tag{3}
f_1 = \frac{d_1}{b_1} \tag{4}
式(2),(3),(4)から式(5)を得ます。
x_1 + e_1x_2 = f_1 \tag{5}
連立方程式の2番目の式は以下の式で(6)表されます。
a_2x_1 + b_2x_2 + c_2x_3 = d_2 \tag{6}
式(5)を式変形し
x_1 = f_1 - e_1x_2 \tag{7}
式(6)に代入します。
a_2(f_1 - e_1x_2) + b_2x_2 - c_2x_3 = d_2 \\
a_2f_1 - a_2e_1x_2 + b_2x_2 - c_2x_3 = d_2 \\
(b_2 - a_2e_1)x_2 + c_2x_3 = d_2 - a_2f_1 \\
x_2 + \frac{c_2}{b_2 - a_2e_1}x_3 = \frac{d_2 - a_2f_1}{b_2 - a_2e_1} \tag{8}
ここで $ e_2,\ f_2 $ は式(9),(10)として、式(11)を得ます。
e_2 = \frac{c_2}{b_2 - a_2e_1} \tag{9}
f_2 = \frac{d_2 - a_2f_1}{b_2 - a_2e_1} \tag{10}
x_2 + e_2x_3 - f_2 \\
x_2 = f_2 - e_2x_3 \tag{11}
式(11)を連立方程式の3番目の式(12)に代入して式(13)を得ます。
a_3x_2 + b_3x_3 + c_3x_4 = d_3 \tag{12}
a_3(f_2 - e_2x_3) + b_3x_3 + c_3x_4 = d_3 \\
a_3f_2 - a_3e_2x_3 + b_3x_3 + c_3x_4 = d_3 \\
(b_3 - a_3e_2)x_3 + c_3x_4 = d_3 - a_3f_2 \\
x_3 + \frac{c_3}{b_3 - a_3e_2} = \frac{d_3 - a_3f_2}{b_3 - a_3e_2} \tag{13}
ここで $ e_3,\ f_3 $ は式(14),(15)として、式(16)を得ます。
e_3 = \frac{c_3}{b_3 - a_3e_2} \tag{14}
f_3 = \frac{d_3 - a_3f_2}{b_3 - a_3e_2} \tag{15}
x_3 = f_3 - e_3x_4 \tag{16}
これを繰り返して、式(17),(18),(19)を得ます。
e_i = \frac{c_i}{b_i - a_ie_{i-1}} \tag{17}
f_i = \frac{d_i - a_if_{i-1}}{b_i - a_ie_{i-1}} \tag{18}
x_{n-1} = f_{n-1} - e_{n-1}x_n \tag{19}
連立方程式の最後の式は式(20)となります。
a_nx_n + b_nx_n = d_n \tag{20}
式(19),(20)から $ x_n $ を求めます。
-a_n(f_{n-1} - e_{n-1}x_n) + b_nx_n = d_n \\
-a_nf_{n-1} - a_ne_{n-1}x_n + b_nx_n = d_n \\
x_n(b_n - a_ne_{n-1}) = d_n - a_nf_{n-1} \\
x_n = \frac{d_n - a_nf_{n-1}}{b_n - a_ne_{n-1}} \tag{21}
$ x_n $ を求めることができたので、式(20)から $ x_{n-1} $ を求め、式(19)から $ x_{n-1, n-2, ... 1} $ を求めます。
ベジェ曲線を計算するプログラム
Tomas のアルゴリズムを使って点からパスを計算するプログラムです。
class CurveAlgorithm {
struct Segment: CustomStringConvertible {
var p0: CGPoint = .zero
var p1: CGPoint = .zero
var p2: CGPoint = .zero
var p3: CGPoint = .zero
var description: String {
"p0: \(p0), p1: \(p1), P2: \(p2), P3: \(p3)"
}
}
static func getSegments(points: [CGPoint]) -> [Segment] {
// points の要素数 - 1がセグメントの個数
let count = points.count - 1
var segments: [Segment] = [Segment](repeating: Segment(), count: count)
// Thomasのアルゴリズムを使ってP1を計算する
// a, b, c, d, e, f を求める
var a: [CGFloat] = []
var b: [CGFloat] = []
var c: [CGFloat] = []
var dX: [CGFloat] = []
var dY: [CGFloat] = []
var e: [CGFloat] = []
var fX: [CGFloat] = []
var fY: [CGFloat] = []
for i in 0..<count {
if i == 0 {
segments[0].p0 = points[0]
segments[0].p3 = points[1]
a.append(0)
b.append(2)
c.append(1)
dX.append(points[0].x + 2 * points[1].x)
dY.append(points[0].y + 2 * points[1].y)
e.append(c[0] / b[0])
fX.append(dX[0] / b[0])
fY.append(dY[0] / b[0])
} else if i == count - 1 {
segments[count - 1].p0 = points[count - 1]
segments[count - 1].p3 = points[count]
a.append(2)
b.append(7)
c.append(0)
dX.append(8 * points[count - 1].x + points[count].x)
dY.append(8 * points[count - 1].y + points[count].y)
} else {
segments[i].p0 = points[i]
segments[i].p3 = points[i + 1]
a.append(1)
b.append(4)
c.append(1)
dX.append(4 * points[i].x + 2 * points[i + 1].x)
dY.append(4 * points[i].y + 2 * points[i + 1].y)
e.append(c[i] / (b[i] - a[i] * e[i - 1]))
fX.append((dX[i] - a[i] * fX[i - 1]) / (b[i] - a[i] * e[i - 1]))
fY.append((dY[i] - a[i] * fY[i - 1]) / (b[i] - a[i] * e[i - 1]))
}
}
// 最後のP1を求める
let x = (dX[count - 1] - a[count - 1] * fX[count - 2]) / (b[count - 1] - a[count - 1] * e[count - 2])
let y = (dY[count - 1] - a[count - 1] * fY[count - 2]) / (b[count - 1] - a[count - 1] * e[count - 2])
segments[count - 1].p1 = CGPoint(x: x, y: y)
// 残りのP1を全て計算する
for i in (1..<count).reversed() {
let x = fX[i - 1] - e[i - 1] * segments[i].p1.x
let y = fY[i - 1] - e[i - 1] * segments[i].p1.y
segments[i - 1].p1 = CGPoint(x: x, y: y)
}
// P2を求める
for i in (0..<count) {
if i == count - 1 {
let x = 0.5 * (points[count].x + segments[i].p1.x)
let y = 0.5 * (points[count].y + segments[i].p1.y)
segments[i].p2 = CGPoint(x: x, y: y)
} else {
let x = 2 * points[i + 1].x - segments[i + 1].p1.x
let y = 2 * points[i + 1].y - segments[i + 1].p1.y
segments[i].p2 = CGPoint(x: x, y: y)
}
}
return segments
}
}
こちらがこの式を使って作成したプログラムでベジェ曲線化したものです。
カクカクしておらず、とても滑らかになっています。
ソースコードは こちら です。
まとめ
- ベジェ曲線は身の回りでたくさん使われています。
- ベジェ曲線を使うことでカクカクを滑らかにできるかもしれません。
- 数式から追いかけるとベジェ曲線のことをもっと知った気になれるのでおすすめです。
少しでもベジェ曲線を身近に感じていただけたら嬉しいです。
ありがとうございました。
参考
おまけ
バーンステイン多項式は以下の関係が成立する。
B^n_i(t)=(1-t)B^{n-1}_{i-1}(t)+tB^{n-1}_{i-1}(t)
二項係数
n = 0
\begin{eqnarray}
\binom{0}{0}=\frac{0!}{(0-1)!0!}=1
\end{eqnarray}
n = 1
i = 0
\begin{eqnarray}
\binom{1}{0}=\frac{1!}{(1-1)!1!}=1
\end{eqnarray}
i = 1
\begin{eqnarray}
\binom{1}{1}=\frac{1!}{(1-1)!1!}=1
\end{eqnarray}
n = 2
i = 0
\begin{eqnarray}
\binom{2}{0}=1
\end{eqnarray}
i = 1
\begin{eqnarray}
\binom{2}{1}=2
\end{eqnarray}
i = 2
\begin{eqnarray}
\binom{2}{2}=1
\end{eqnarray}
n = 3
\begin{eqnarray}
\binom{3}{0}=1, \binom{3}{1}=3, \binom{3}{2}=3, \binom{3}{3}=1
\end{eqnarray}
二項係数はパスカルの三角形になる
\begin{array}{c}
1 \\
1\ 1\\
1\ 2\ 1\\
1\ 3\ 3\ 1\\
1\ 4\ 6\ 4\ 1\\
1\ 5\ 10\ 10\ 5\ 1\\
1\ 6\ 15\ 20\ 15\ 6\ 1\\
1\ 7\ 21\ 35\ 35\ 21\ 7\ 1\\
\end{array}
n=1
\begin{eqnarray}
B^1_0(t)=1-t
\end{eqnarray}
\begin{eqnarray}
B^1_0(t)=t
\end{eqnarray}
n=2
\begin{eqnarray}
B^2_0(t)=(1-t)^2
\end{eqnarray}
\begin{eqnarray}
B^2_1(t)=2t(1-t)
\end{eqnarray}
\begin{eqnarray}
B^2_2(t)=t^2
\end{eqnarray}