この記事の概要
機械学習の説明性の研究として,Example-Basedな説明があります.この記事では,説明性の研究のトップランナーの一人である, Been Kimをファーストオーサーとする論文,
"Examples are not Enough, Learn to Criticize! Criticism for Interpretability",https://people.csail.mit.edu/beenkim/papers/KIM2016NIPS_MMD.pdf について書いています.
Examples are not Enough
機械学習の説明性の1つとして, Example-Basedな説明があげられます. 我々人間も, Example-Basedな意志決定をしています. 例えば弁護士さんなら, 新しいクライアントに似た過去の事例を徹底的に調べ上げ, 何かしらの意志決定をします(多分).
機械学習においても, あるデータ分布を説明するために, 代表のデータをピックアップするというような手法がとられます. しかし, Example,すなわち代表的なデータだけでは不十分です(Examples are not enough). なぜならOver-generalizationや誤解が生まれる可能性があるからです.
どーゆうこと???
私は情報工学を専攻しています. 例えば, 情報工学の人に趣味を聞いてみることを考えてみましょう. しかし,全員には聞く体力はないとします. A君に聞いてみたら,「プログラミング」と答えました. 次にB君に聞いてみたらB君も「プログラミング」と答えました. C君もD君もそう答えました. すると, "情報工学専攻の学生はみんなプログラミング好き"という結論を導いてしまう,"かも"しれません. つまり一般化が行きすぎてしまうんです(Over-generalization). ここら辺は, 認知科学とも関係があるそうです.
論文の概論
Anyway, Examples are not enoughなわけです. そこでこの論文では, MMD-criticというフレームワークを提案しています. MMD-criticを使うと,データの代表的な例(Prototypes)だけでなく,少し変わった例(Criticisms)もピックアップしてくれます. 下図が論文に載っている, MMD-criticを使って抽出したPrototypesとCriticismsです.
 (原論文より引用)
(原論文より引用)
右の犬のCriticismsには, 被り物??をかぶっている画像など, 少しイレギュラーな画像があげられており,Criticisms(代表的な例とは少し離れているデータ)を取れています. この論文の概要としては,MMD-criticの提案, ImageNetの画像と手書き文字画像をMMD-criticにかける実験, Pilot Studyとして, PrototypesとCriticismsを提示することがユーザにとって本当にプラスになるかどうかの実験をし, それぞれ結果を載せています.
MMD-criticの理論
MMD-criticの理論について書いていきます. MMD-criticは, 名前の通り, MMD(Maximum Mean Discrepancy)を利用します. 使う材料(キーワード)は以下の通りです.
- MMD(Maximum Mean Discrepancy)
- witness function
- カーネル関数
- 単調劣モジュラ関数の性質
- 貪欲法
MMDの定義から行きましょう. 定義は以下になります.
$$MMD(F,P,Q) = sup_{f\in{F}}(E_{X\verb|~|P}[f(X)]-E_{X\verb|~|Q}[f(X)])
$$
Fは関数空間です. P,Qをそれぞれ何かしらのデータ分布(Distributions)としています. MMDとは式から, 2つの分布のデータを関数fに与えた時の期待値の差の上限(Maximum)です.つまり,P,Qの分布がどのくらい違うかを表します. ここで, Fが再生核ヒルベルト空間であるとき(なんやねんそれ),上限が以下のようになります.
$$f(x) = E_{X'\verb|~|P}[k(x,X')]-E_{X'\verb|~|Q}[k(x,X')]
$$
これをwitness functionといいます. k(・,・)はカーネル関数です. 分布Qが分布Pにunderfitしている時は,witness functionはプラスに, 逆にoverfitしているときはマイナスになります. とりあえず, これも2つの分布の最大の不一致度(Discrepancy)を見ています.
これを実際に計算するためには, いくらかサンプルをとります. そして, MMDもMMDの二乗を使います. MMDの二乗をして,supの部分をwitness functionを利用すると, 最終的な式として,以下が得られます.
$$MMD^2(F,X,Z)=\frac{1}{n^2}\sum_{i,j\in{[n]}}k(x_i,x_j)-\frac{2}{nm}\sum_{i\in{[n]},j\in{[m]}}k(x_i,z_j)+\frac{1}{m^2}\sum_{i,j\in{[m]}}k(z_i,z_j)$$
Xが分布Pからn個サンプルした集合で, Zが分布Qからm個サンプルした集合です. つまり,データをサンプルしてそれをカーネル関数にかけて,どのくらい似ているか・一致しているかを見ています.
以上の考えを, MMD-criticでは利用します. すなわち, Xを観測されたデータ全体だとして, ZをPrototypesとして取ったデータと考えます. そうすると,Prototypesとしてふさわしいのは, MMDの2乗を最小化するデータの集合です. なぜなら取ってきたPrototypes(代表例)は元の観測データの分布を良く表していてほしいからです.図にすると下図のようになります.
以下は,https://christophm.github.io/interpretable-ml-book/proto.html からの画像です. MMDの値が小さいほど,元の分布に似ていることがわかります.赤い点が選ばれたPrototypesです.
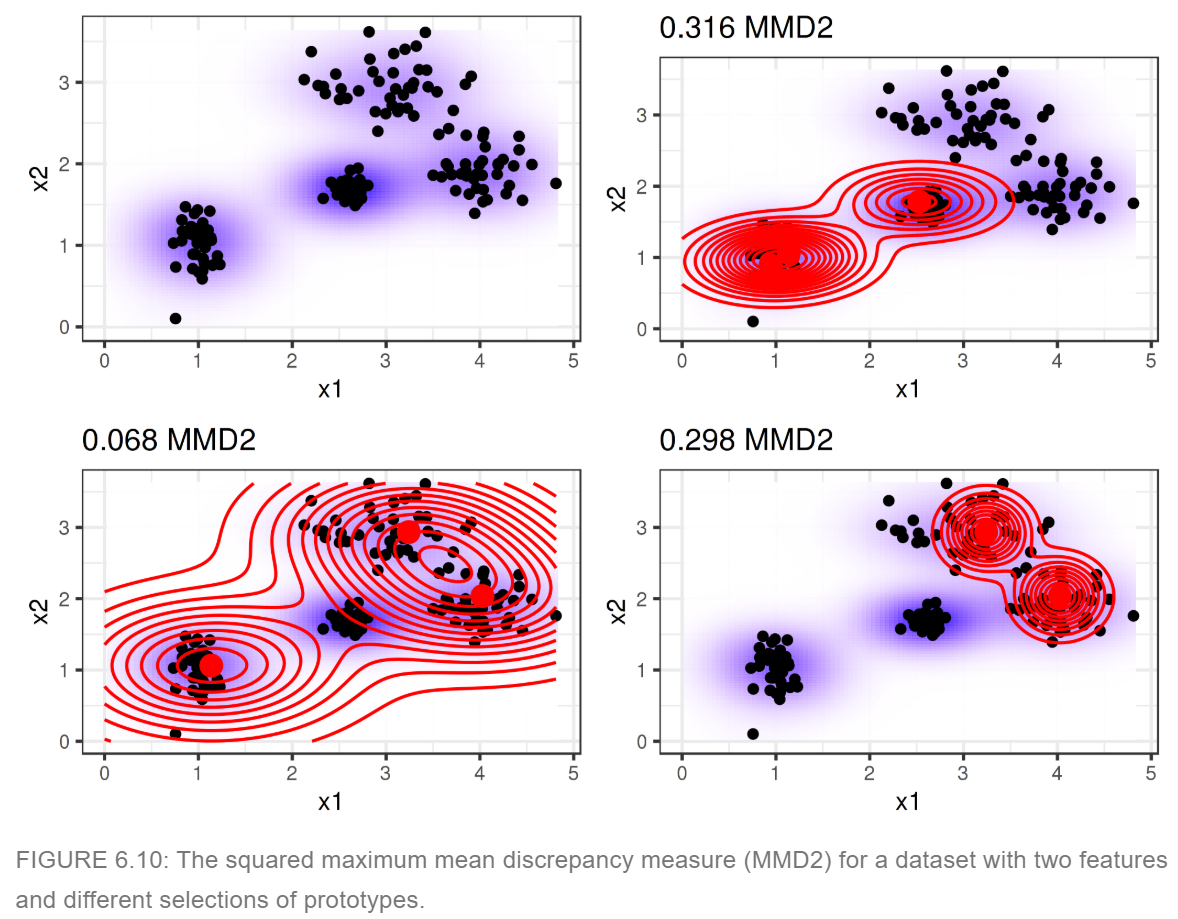
(Interpretable Machine Leaningより
https://christophm.github.io/interpretable-ml-book/)
では,どのようにMMDを最小化するPrototypesの集合を決めるのでしょうか. ここで劣モジュラ関数の考えが出てきます. つまりMMD-criticがやっているのは, 最適な部分集合の決定(元のデータ分布を良く表す代表的な例,つまりPrototypesの決定)に他ならないので,離散最適化問題の1種といえます.論文では, MMD^2を最小化するのではなく-MMD^2を最大化することを考えます. つまりコスト関数
$$J(S)=\frac{1}{n^2}\sum_{i,j=1}^nk(x_i,x_j)-MMD^2(F,X,X_s)$$
を最大化します.ここで, 右辺第1項はadditive biasです. Xは観測データ,X_sはXのsubset,つまり選ぼうとしているPrototypesの集合です(今更ですが,Prototypesの数はハイパーパラメタ).論文では, これがある条件下で単調劣モジュラ関数であることが示されています. コスト関数が単調劣モジュラ関数であるので, 私たちはこれを貪欲法で一応解けるのです.
劣モジュラ関数に関してはこちらがめちゃわかりやすいです.
(参照)プリキュアで学ぶ劣モジュラ関数
https://tasusu.hatenablog.com/entry/2015/12/01/000608
MMD-criticのアルゴリズム
MMD-criticのアルゴリズムについて書いていきます.
MMD-criticは最初に述べたように,PrototypesとCriticismsを選択します. 両方とも考えの流れは大体同じなので,Prototypesの選択のアルゴリズムのみ書いています.
以下がアルゴリズムになります.

(原論文より)
画像にもあるように,Greedy Algorithm,すなわち貪欲法でPrototypesを選択しています. Sが選ばれたPrototypesの集合で,mが取ってくるPrototypesの個数です(ハイパーパラメタ). 貪欲法なので, 貪欲に全体データ数nに対して,集合関数F(上述のJ(S))を計算します(foreachの部分).そして, Prototypesの集合Sに追加したときにMMDの2乗が一番最小化されるようにデータiを選びます(argmax f_iの部分). もちろん前に述べたように, 集合関数J(S)を最大化するように選ぶとも言えます.
どのみちやっていることは, Prototypesを選んだときに元々のデータ分布を良く表せているようにアルゴリズムが動きます.
自分で実験
コードはここです.
なんか見れない気がするのでこちらも.
論文では, USPS?という手書き文字で実験していました. なので同じ手書き文字ですが, mnistの中の5000枚に対してMMD-criticをかけました.結果は以下のようになりました.
Prototypes↓↓↓

確かに, Criticisms, 取れている, よね???
おわりに
Pilot Studyの実験等については, 原論文を見てみてください. もちろん結果としては, Criticisms出した方がUser-Friendlyな説明となるよ, みたいな感じです.
著者のコード.https://github.com/BeenKim/MMD-critic
著者のMMD-criticに関するスライド. http://people.csail.mit.edu/beenkim/slides/Kim2016MMD_final_pdf.pdf
Thank you for reading
